目的
1自由度系(バネマスダンバ系)の状態方程式を立式し、Python Controlで、状態方程式から伝達関数へと変換する。
比較として、ラプラス変換から、伝達関数を求める方法も記載も記載する。
事前準備
状態方程式と伝達関数
状態方程式とは、以下の式によって表される。
\dot{x}(t)=Ax(t)+Bu(t) \\
y(t)=Cx(t)+Du(t)
状態方程式をラプラス変換すると、
sX(s)=AX(s)+BU(s) \\
Y(s)=CX(s)+DU(s)
式を変換すると、
sX(s)-AX(s)=BU(s) \\
(sI-A)X(s)=BU(s) \\
X(s)={(sI-A)}^{-1} BU(s) \\
伝達関数G(s)は
G(s)=\frac{Y(s)}{U(s)}=\frac{{(sI-A)}^{-1} BU(s) +DU(s)}{U(s)}=(sI-A)^{-1} B +DU
から求まる。
Python-Controlでは、
control.ss2tf関数にA,B,C,Dの行列を入力すると、上式に従い、伝達関数を求めることができる。
http://python-control.readthedocs.io/en/latest/generated/control.ss2tf.html
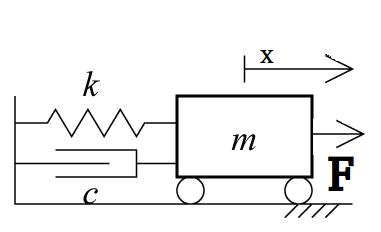
状態方程式の立式
m:質量[kg]
k:ばね定数[N/m]
c:粘性減衰係数[N・s/m]
f:力[N]
とおくと、
上記の運動方程式は、
m\ddot{x}+c\dot{x}+kx=f \\
となる。
状態方程式から伝達関数を求める。
ここで式を変形して、
m\ddot{x}+c\dot{x}+kx=f \\
m\ddot{x}=-c\dot{x}-kx+f \\
\ddot{x}=-c/m \dot{x}-k/m x+f/m \\
とする。
x_{1}=x \\
x_{2}=\dot{x} \\
とおくと、
\\
\dot x_{1} ={x_{2}} \\
\dot x_{2}= -c/m \dot{x_{2}}-k/m x_{1}+f/m \\
これを行列で書くと
\\
\begin{bmatrix}
\dot x_{1} \\
\dot x_{2}
\end{bmatrix}
=
\begin{bmatrix}
0 & 1 \\
-k/m & -c/m
\end{bmatrix}
\begin{bmatrix}
x_{1} \\
x_{2}
\end{bmatrix}
+
\begin{bmatrix}
0 \\
1/m
\end{bmatrix}
f
さらに、
y=x とすると、\\
y=
\begin{bmatrix}
1 & 0
\end{bmatrix}
\begin{bmatrix}
x_{1} \\
x_{2}
\end{bmatrix}
よって、
\\
\begin{bmatrix}
\dot x_{1} \\
\dot x_{2}
\end{bmatrix}
=
\begin{bmatrix}
0 & 1 \\
-k/m & -c/m
\end{bmatrix}
\begin{bmatrix}
x_{1} \\
x_{2}
\end{bmatrix}
+
\begin{bmatrix}
0 \\
1/m
\end{bmatrix}
f \\
y=
\begin{bmatrix}
1 & 0
\end{bmatrix}
\begin{bmatrix}
x_{1} \\
x_{2}
\end{bmatrix}
状態方程式と比較すると、
x(t)=
\begin{bmatrix}
x_{1} \\
x_{2}
\end{bmatrix}
,
u(t)=f
,
A=
\begin{bmatrix}
0 & 1 \\
-k/m & -c/m
\end{bmatrix}
,
B=
\begin{bmatrix}
0 \\
1/m
\end{bmatrix}
,
C=
\begin{bmatrix}
1 & 0
\end{bmatrix}
,
D=[0]
となる。
以上から、
python controlで伝達関数を求めるコードは以下の様になる。
-signal_degree_of_freedom_system_1.py
# !/usr/bin/env python
from control.matlab import *
from matplotlib import pyplot as plt
def main():
k=3.0
m=0.1
c=0.01
A = [[0., 1], [-k/m, -c/m]]
B = [[0.], [1./m]]
C = [[1., 0.0]]
D = [[0.]]
sys1 = ss2tf(A, B, C, D)
print sys1
bode(sys1)
plt.show()
if __name__ == "__main__":
main()
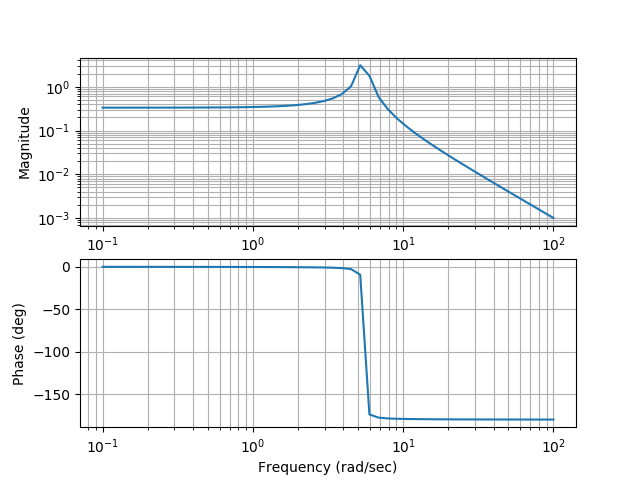
実行結果
$ ./signal_degree_of_freedom_system_1.py
10
----------------
s^2 + 0.1 s + 30
状態方程式をラプラス変換して伝達関数を求める。
状態方程式の立式から、u(t)=fとした場合、
m\ddot{x}(t)+c\dot{x}(t)+kx(t)=u(t) \\
をラプラス変換すると
ms^2X(s)+cX(s)+kX(s)=U(s) \\
さらに、y=xとすると、
ms^2Y(s)+cY(s)+kY(s)=U(s) \\
\frac{Y(s)}{U(s)}=\frac{1}{ms^2+cs+k}
伝達関数は、
G(s)=\frac{Y(s)}{U(s)}=\frac{1}{ms^2+cs+k}
以上から、
python controlで伝達関数を求めるコードは以下の様になる。
# !/usr/bin/env python
from control.matlab import *
from matplotlib import pyplot as plt
def main():
k=3.0
m=0.1
c=0.01
num = [0, 0,1]
den = [m, c, k]
sys = tf(num, den)
print sys
bode(sys)
plt.show()
if __name__ == "__main__":
main()
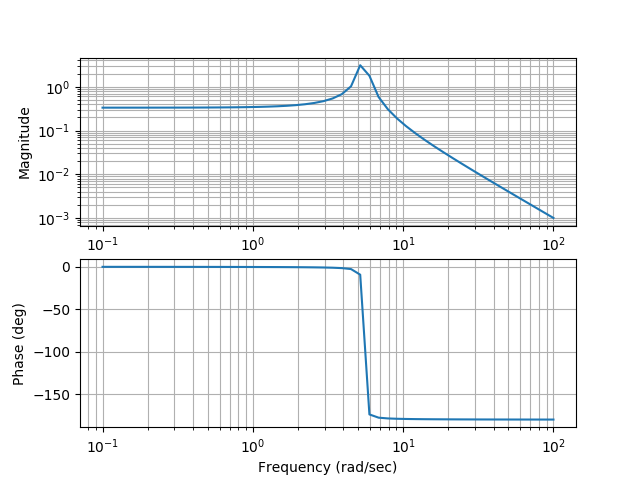
実行結果
$ ./signal_degree_of_freedom_system_2.py
1
--------------------
0.1 s^2 + 0.01 s + 3
サンプルコード
サンプルコードは以下に格納。
https://github.com/nnn112358/python-control_test