Python ControlでAircraftの制御設計を行う(前編)

###目的
Python ControlでAircraft:垂直離着陸機の制御設計を行う。

この記事は、Python Controlのexampleに含まれているカリフォルニア工科大学 Richard教授の資料を和訳したものです。
Python-control/Example: Vertical takeoff and landing aircraft
Python-control/Example: pvtol-lqr.py

###事前準備
PythonControlをインストールする

---

####はじめに
このページでは、Karl J. Åström と Richard M. Murrayによるフィードバックシステムのテキストにて、実例として使用されているベクトルスラスト航空機モデルのコントローラの解析と設計にPython Controlパッケージを使用する方法を示します。
この例では、MATLAB互換コマンドを使用しています。次のファイルには、ここに示すコードが含まれています。

pvtol-lqr.py - 状態フィードバックコントローラの設計
pvtol-nested.py -伝達関数を用いた内外ループ設計

####システムの説明
この例では、（平面）垂直離着陸機（PVTOL）の簡易モデルを使用しています。以下に示します。

航空機の質量中心の位置および方向は、（x、y、θ）で表され、mは車両の質量、Jは慣性モーメント、gは重力定数、cは減衰係数です。
メイン下向きスラスタおよび操縦スラスタによって生成された力は、航空機の下方の距離r（スラスタの幾何学的形状によって決定される）で作用する1対の力F1およびF2としてモデル化されます。
原点がゼロ入力のシステムの平衡点になるように入力を再定義すると便利です。
式をu1= F1、u2 = F2-mgとすると、式は次のように状態空間形式で書くことができる。

Parameter	Value	Comment
m	4 kg	system 質量
J	0.0475 kg m^2	system 慣性
r	0.25 m	推力オフセット
g	9.8 m/s	重力
c	0.05 N s/m	回転減衰

####LQR 状態フィードバックコントローラ
このセクションでは、ベクトルスラスト飛行機の例のLQR状態フィードバックコントローラの設計を示します。
この例は、Karl J. Åström と Richard M. Murrayによるフィードバックシステムの第6章（状態フィードバック）から抜粋したものです。
ここにリストされているPythonコードは、ファイルpvtol-lqr.pyに含まれています
。
この例を実行するには、最初にSciPy、MATLABプロット、およびpython-controlパッケージ用のライブラリをインポートします。

from numpy import *             # NumPy関数
from matplotlib.pyplot import * # MATLAB プロット関数
from control.matlab import *    # MATLAB-like 関数

システムのパラメータは、

m = 4;                         # aircraftの質量
J = 0.0475;                    #ピッチ軸周りの慣性
r = 0.25;                      #力の中心までの距離
g = 9.8;                       # 重力定数
c = 0.05;                      # 減衰係数（推定値）

平衡点付近

x_e =（0,0,0,0,0,0）、u_e =（0,mg）

のダイナミクスの線形化によって、

#  dynamicsの状態空間
xe = [0, 0, 0, 0, 0, 0];        # 平衡点
ue = [0, m*g];                  # (これらはリストであり行列ではないことに注意してください)

# Dynamics 行列 (*が動作するように行列型を使用する)
A = matrix(
   [[ 0,    0,    0,    1,    0,    0],
    [ 0,    0,    0,    0,    1,    0],
    [ 0,    0,    0,    0,    0,    1],
    [ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
    [ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
    [ 0,    0,    0,    0,    0,    0 ]])

# Input 行列
B = matrix(
   [[0, 0], [0, 0], [0, 0],
    [cos(xe[2])/m, -sin(xe[2])/m],
    [sin(xe[2])/m,  cos(xe[2])/m],
    [r/J, 0]])

# Output 行列 
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])

システムの線形二次レギュレータを計算するために、コスト関数を

ここで、z = z-ze およびv = u-ue は、所望の平衡点（ze、ue）を中心とするローカル座標を表します。
まず、状態コストと入力コストの対角行列から始めます。

Qx1 = diag([1, 1, 1, 1, 1, 1]);
Qu1a = diag([1, 1]);
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K);

ここで、v = -Kzの制御則を与え、それを元にして制御則を導出することができます。

ここで、ud=(0,mg) 、zd=(xd,yd,0,0,0,0)

python制御パッケージはSISOシステムのみをサポートしているため、閉ループ動特性を計算するためには、横方向および高度のダイナミクスを個々のシステムとして抽出する必要があります。
更に、Kxdを入力ベクトルとするstepコマンドを使用して閉ループ動特性をシミュレートします。
（入力がユニットサイズで、xdが希望の定常状態に対応すると仮定します）。

xd = matrix([[1], [0], [0], [0], [0], [0]]); 
yd = matrix([[0], [1], [0], [0], [0], [0]]);  

# Indices for the parts of the state that we want
lat = (0,2,3,5);
alt = (1,4);

# Decoupled dynamics
Ax = (A[lat, :])[:, lat];       #! not sure why I have to do it this way
Bx = B[lat, 0]; Cx = C[0, lat]; Dx = D[0, 0];
 
Ay = (A[alt, :])[:, alt];       #! not sure why I have to do it this way
By = B[alt, 1]; Cy = C[1, alt]; Dy = D[1, 1];

# Step response for the first input
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);
(Tx, Yx) = step(H1ax, T=linspace(0,10,100));

# Step response for the second input
H1ay = ss(Ay - By*K1a[1,alt], By*K1a[1,alt]*yd[alt,:], Cy, Dy);
(Ty, Yy) = step(H1ay, T=linspace(0,10,100));

plot(Tx, Yx[0,:].T, '-', Ty, Yy[0,:].T, '--'); hold(True);
plot([0, 10], [1, 1], 'k-'); hold(True);
ylabel('position');
legend(('x', 'y'), loc='lower right');

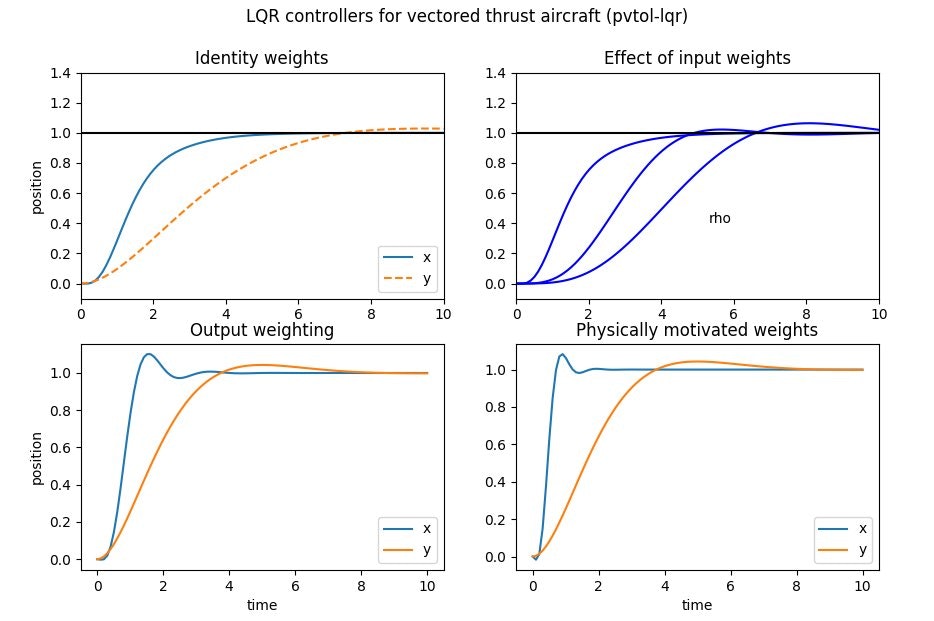
所望の位置のステップ変化に対する閉ループシステムの応答を以下に示します。

左のプロットは、各方向に1m移動するように命じられたときの航空機のxとyの位置を示しています。
応答は、LQRコストの重みを調整することで調整できます。右のプロットは、制御重み　rho = 1,10^2、10^4でのxの動きを示しています。コスト関数における入力項の重みが高ければ、応答はより緩慢になります。コードを使用して作成することができます。

# Look at different input weightings
Qu1a = diag([1, 1]); (K1a, X, E) = lqr(A, B, Qx1, Qu1a);
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);

Qu1b = (40**2)*diag([1, 1]); (K1b, X, E) = lqr(A, B, Qx1, Qu1b);
H1bx = ss(Ax - Bx*K1b[0,lat], Bx*K1b[0,lat]*xd[lat,:],Cx, Dx);

Qu1c = (200**2)*diag([1, 1]); (K1c, X, E) = lqr(A, B, Qx1, Qu1c);
H1cx = ss(Ax - Bx*K1c[0,lat], Bx*K1c[0,lat]*xd[lat,:],Cx, Dx);

[T1, Y1] = step(H1ax, T=linspace(0,10,100));
[T2, Y2] = step(H1bx, T=linspace(0,10,100));
[T3, Y3] = step(H1cx, T=linspace(0,10,100));

plot(T1, Y1[0,:].T, 'b-'); hold(True);
plot(T2, Y2[0,:].T, 'b-'); hold(True);
plot(T3, Y3[0,:].T, 'b-'); hold(True);
plot([0 ,10], [1, 1], 'k-'); hold(True);

axis([0, 10, -0.1, 1.4]); 
# arcarrow([1.3, 0.8], [5, 0.45], -6);
text(5.3, 0.4, 'rho');

---

####pvtol-lqr.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

# pvtol_lqr.m - LQR design for vectored thrust aircraft
# RMM, 14 Jan 03
#

#このファイルは、Astrom and Mruray第5章の平面垂直離着陸（PVTOL）航空機の例を使用して、
#LQRベースの設計上の問題をPythonコントロールパッケージの基本機を使って処理します。
#

from numpy import *             # NumPy関数
from matplotlib.pyplot import * # MATLAB プロット関数
from control.matlab import *    # MATLAB-like 関数

#
# System dynamics
#
# 状態空間形式のPVTOLシステムのダイナミクス
#

# システムのパラメータ
m = 4;                         # aircraftの質量
J = 0.0475;                    #ピッチ軸周りの慣性
r = 0.25;                      #力の中心までの距離
g = 9.8;                       # 重力定数
c = 0.05;                      # 減衰係数（推定値）


#  dynamicsの状態空間
xe = [0, 0, 0, 0, 0, 0];        # 平衡点
ue = [0, m*g];                  # (これらはリストであり行列ではないことに注意してください)

# Dynamics 行列 (*が動作するように行列型を使用する)
A = matrix(
    [[ 0,    0,    0,    1,    0,    0],
     [ 0,    0,    0,    0,    1,    0],
     [ 0,    0,    0,    0,    0,    1],
     [ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
     [ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
     [ 0,    0,    0,    0,    0,    0 ]])

# Input 行列
B = matrix(
    [[0, 0], [0, 0], [0, 0],
     [cos(xe[2])/m, -sin(xe[2])/m],
     [sin(xe[2])/m,  cos(xe[2])/m],
     [r/J, 0]])

# Output 行列 
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])

#
#　xy位置のstepに対応する入力と出力を構築する
#ベクトルxdおよびydは、システムの所望の平衡状態である状態に対応する。
#行列CxおよびCyは、対応する出力である。
#
# これらのベクトルは、閉ループシステムのダイナミクスを次のように計算することで使用される。

#
#	xdot = Ax + B u		=>	xdot = (A-BK)x + K xd
#         u = -K(x - xd)		   y = Cx
#
# 閉ループ動特性は、入力ベクトルとしてK * xdを用いて「step」コマンドを使用してシミュレートすることができる
# （「入力」は単位サイズであると仮定し、xdは所望の定常状態に対応する）。
#

xd = matrix([[1], [0], [0], [0], [0], [0]]); 
yd = matrix([[0], [1], [0], [0], [0], [0]]);  

#
# 関連するダイナミクスを抽出してSISOライブラリで使用する
#
# 現在のpython-controlライブラリはSISO転送関数しかサポートしていないので、
# 元のMATLABコードの一部を修正してSISOシステムを抽出する必要があります。
# これを行うために、横（x）および縦（y）ダイナミクスに関連する状態からなるように、
# 「lat」および「alt」インデックスベクトルを定義します。
#

# 状態変数
lat = (0,2,3,5);
alt = (1,4);

#分離されたダイナミックス
Ax = (A[lat, :])[:, lat];       #!なぜこのようにしなければならないのか分からない!
Bx = B[lat, 0]; Cx = C[0, lat]; Dx = D[0, 0];

Ay = (A[alt, :])[:, alt];       #!なぜこのようにしなければならないのか分からない!
By = B[alt, 1]; Cy = C[1, alt]; Dy = D[1, 1];

#  plotラベル
clf(); 
suptitle("LQR controllers for vectored thrust aircraft (pvtol-lqr)")

#
# LQR design
#

# 対角行列の重み付け
Qx1 = diag([1, 1, 1, 1, 1, 1]);
Qu1a = diag([1, 1]);
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K);

# ループを閉じる: xdot = Ax - B K (x-xd)
# Note: python-controlでは、この入力を一度に行う必要があります
#　H1a = ss(A-B*K1a, B*K1a*concatenate((xd, yd), axis=1), C, D)　
# (T, Y) = step(H1a, T=linspace(0,10,100));

# 最初の入力に対するステップ応答
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);
(Yx, Tx) = step(H1ax, T=linspace(0,10,100));

# 第2入力に対するステップ応答
H1ay = ss(Ay - By*K1a[1,alt], By*K1a[1,alt]*yd[alt,:], Cy, Dy);
(Yy, Ty) = step(H1ay, T=linspace(0,10,100));

subplot(221); title("Identity weights")
# plot(T, Y[:,1, 1], '-', T, Y[:,2, 2], '--'); hold(True);
plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); hold(True);
plot([0, 10], [1, 1], 'k-'); hold(True);

axis([0, 10, -0.1, 1.4]); 
ylabel('position');
legend(('x', 'y'), loc='lower right');

# 異なる入力重みを見る
Qu1a = diag([1, 1]); (K1a, X, E) = lqr(A, B, Qx1, Qu1a);
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);

Qu1b = (40**2)*diag([1, 1]); (K1b, X, E) = lqr(A, B, Qx1, Qu1b);
H1bx = ss(Ax - Bx*K1b[0,lat], Bx*K1b[0,lat]*xd[lat,:],Cx, Dx);

Qu1c = (200**2)*diag([1, 1]); (K1c, X, E) = lqr(A, B, Qx1, Qu1c);
H1cx = ss(Ax - Bx*K1c[0,lat], Bx*K1c[0,lat]*xd[lat,:],Cx, Dx);

[Y1, T1] = step(H1ax, T=linspace(0,10,100));
[Y2, T2] = step(H1bx, T=linspace(0,10,100));
[Y3, T3] = step(H1cx, T=linspace(0,10,100));

subplot(222); title("Effect of input weights")
plot(T1.T, Y1.T, 'b-'); hold(True);
plot(T2.T, Y2.T, 'b-'); hold(True);
plot(T3.T, Y3.T, 'b-'); hold(True);
plot([0 ,10], [1, 1], 'k-'); hold(True);

axis([0, 10, -0.1, 1.4]); 

# arcarrow([1.3, 0.8], [5, 0.45], -6);
text(5.3, 0.4, 'rho');

# 出力重み付け - 出力を使用するようにQxを変更する
Qx2 = C.T * C;
Qu2 = 0.1 * diag([1, 1]);
(K, X, E) = lqr(A, B, Qx2, Qu2); K2 = matrix(K)

H2x = ss(Ax - Bx*K2[0,lat], Bx*K2[0,lat]*xd[lat,:], Cx, Dx);
H2y = ss(Ay - By*K2[1,alt], By*K2[1,alt]*yd[alt,:], Cy, Dy);

subplot(223); title("Output weighting")
[Y2x, T2x] = step(H2x, T=linspace(0,10,100));
[Y2y, T2y] = step(H2y, T=linspace(0,10,100));
plot(T2x.T, Y2x.T, T2y.T, Y2y.T)
ylabel('position');
xlabel('time'); ylabel('position');
legend(('x', 'y'), loc='lower right');

#
# 　物理的に動機付けされた重み付け
#
# xで1 cmの誤差、yで10 cmの誤差で決定する。
# 角度を5度以下に調整して調整する。
# 効率の低下により、サイドの力にはペナルティを課す。
#

Qx3 = diag([100, 10, 2*pi/5, 0, 0, 0]);
Qu3 = 0.1 * diag([1, 10]);
(K, X, E) = lqr(A, B, Qx3, Qu3); K3 = matrix(K);

H3x = ss(Ax - Bx*K3[0,lat], Bx*K3[0,lat]*xd[lat,:], Cx, Dx);
H3y = ss(Ay - By*K3[1,alt], By*K3[1,alt]*yd[alt,:], Cy, Dy);
subplot(224)
# step(H3x, H3y, 10);
[Y3x, T3x] = step(H3x, T=linspace(0,10,100));
[Y3y, T3y] = step(H3y, T=linspace(0,10,100));
plot(T3x.T, Y3x.T, T3y.T, Y3y.T)
title("Physically motivated weights")
xlabel('time'); 
legend(('x', 'y'), loc='lower right');

show()

---

サンプルコードは以下に格納。
https://github.com/nnn112358/python-control_test

###参考
PythonControlをインストールする
PythonControlで1自由度系の伝達関数を求める。
PythonControlで2自由度系の伝達関数を求める。