はじめに
- OpenCVには、画像の特徴点検出や、2枚の画像間の同じ特徴点ペアを見つける機能があります。
- このペア情報から、2枚の画像間の向きを求める方法として、エピポーラ幾何が知られてます。
- この技術を使って、映像からカメラ方向の解析を試しました。
前提
特徴点のペアが10点以上見つからないような画像では答えが求められません。
工夫したこと
-
1フレーム目のカメラ方向を正面として計算
mp4動画を入力し、1フレーム目画像に対する2フレーム目以降のカメラ方向を求めます。 -
方向を示す行列$R$の推定
$R$の候補は2つ出てくるので、トレースの大きさを利用して決めました。 -
結果を映像表示
方向の変化がわかるよう角度計算、また座標軸を映像に追記して表示します。
内容
1. PC環境
実施したPC環境は以下のとおりです。
| CPU | Celeron N4100 |
| メモリ | 8GB LPDDR4 |
2. 前準備
Windowsで使えるようにするため、以下のツール / システムをインストールしました。
インストール時に参考にしたサイトも記載します。
-
python(使用したのはVer.3.7 )
実行時のベースシステムです。
(参考)https://qiita.com/ssbb/items/b55ca899e0d5ce6ce963 -
pip(使用したのはVer.21.2.4 )
他のツールをダウンロードする際に使うツールです。
(python3系ではバージョン3.4以降であれば、pythonのインストールと共にpipもインストールされます。)
(参考)https://gammasoft.jp/python/python-library-install/ -
OpenCV(使用したのはVer.4.5.3.56 )
画像系処理するためのライブラリです。
(参考)https://qiita.com/ideagear/items/3f0807b7bde05aa18240 -
OpenCV_contrib(使用したのはVer.4.5.3 )
OpenCVの拡張モジュールです。※特徴点検出機能AKAZEを使うのに必要です。
(参考)https://qiita.com/fiftystorm36/items/1a285b5fbf99f8ac82eb -
numpy(使用したのVer.4.7.0.72)
線形代数計算が得意な数値計算モジュールです。
(参考)https://qiita.com/butako/items/15d7cb5aaef90b09ccd8
3. pyファイルの作成
組んだコードは次のとおりです。
import sys
import numpy as np
import numpy.linalg as LA
import cv2
#映像元を設定 camera
camera = cv2.VideoCapture("./in_movie.mp4") # 動画を指定
#画像のスケーリングパラメータを設定 scal ※画像が大きいと時間がかかるため
scal = 1.0
#カメラ内部パラメータを設定 K
w = int(640/scal)
h = int(480/scal)
tans = np.tan(np.deg2rad(36.54))
K = np.array([[w/2.0/tans,0,w/2.0],[0,w/2.0/tans,h/2.0],[0,0,1]])
#映像出力writerを設定 writer
frame_rate = 15.0
size = (w, h)
fmt = cv2.VideoWriter_fourcc('m', 'p', '4', 'v') # mp4
writer = cv2.VideoWriter('./out_movie.mp4', fmt, frame_rate, size)
#特徴検出の関数を設定 detector
#--Detector character points
detector = cv2.AKAZE_create()
#マッチング関数を設定 match
match = cv2.BFMatcher()
#------
#START(Enterキーを押すまで一時停止)
a = input("hit enter key")
#画像1を処理
# フレームを取得
ret, img1i = camera.read()
#スケーリング
window_l = cv2.resize(img1i, dsize=(int(img1i.shape[1]/scal),int(img1i.shape[0]/scal)))
#特徴検出
k1, d1 = detector.detectAndCompute(window_l,None)
#------
#ループ処理
while True:
#画像2を処理
# フレームを取得
ret, img2i = camera.read()
#スケーリング
window_r = cv2.resize(img2i, dsize=(int(img2i.shape[1]/scal),int(img2i.shape[0]/scal)))
#特徴検出
k2, d2 = detector.detectAndCompute(window_r,None)
#------
#マッチング
matches = match.knnMatch(d1, d2, k=2)
#マッチングペアの確認:ペアの数が10以下なら、ストップ
good = []
for m, n in matches:
if m.distance < 0.8* n.distance:
good.append(m)
MIN_MATCH_COUNT = 10
if len(good) > MIN_MATCH_COUNT:
ptsCAM1i = np.int32([ k1[m.queryIdx].pt for m in good ])
ptsCAM2i = np.int32([ k2[m.trainIdx].pt for m in good ])
else:
print('Not enough matches are found - {}/{}'.format(len(good), MIN_MATCH_COUNT))
exit(1)
##--------------------------------------------------------------------
#エピポーラ幾何の計算
#マッチングペアから基礎行列F、基本行列Eを求め、回転行列Rを計算、回転角度α、β、γを算出
#<< 画像1 → 画像2 の向き変化を計算する仕組み >>
#基礎行列F,及びmaskの取得
F, mask = cv2.findFundamentalMat(ptsCAM2i, ptsCAM1i, cv2.FM_LMEDS)
#基本行列の取得
E = np.dot(np.dot(K.T,F),K)
#Rの取得
#次正方行列 U,Σ,V(転置行列)を求める
U, S, Vt = LA.svd(E, full_matrices=True)
W = np.array([[0,-1,0],[1,0,0],[0,0,1]])
R1 = np.dot(np.dot(U,W),Vt)
WT = W.T
R2 = np.dot(np.dot(U,WT),Vt)
#候補のRを選ぶ。トレースから推定
if np.abs(np.trace(R1)) > np.abs(np.trace(R2)):
R = R1
else:
R = R2
#Rに反転が入ってた場合は、再反転して戻す。
if np.trace(R) < 0 :
R = -R
#カメラの向きで見て、座標系を「X:左→右、Y:上↓下、Z:後→前」」と定義し、R = Rz(α)Ry(β)Rx(γ)と分解したときの角度を計算
alpha = np.rad2deg(np.arctan2(R[1][0],R[0][0]))
beta = np.rad2deg(np.arctan2(-R[2][0], np.sqrt(R[0][0]**2+R[1][0]**2)))
gamma = np.rad2deg(np.arctan2(R[2][1],R[2][2]))
##-----------------------------------------------------------------------------
#結果を画像と共に表示、
# 実際に使用された特徴点のみを描画のために取得
ptsCAM2i = ptsCAM2i[mask.ravel() == 1]
#使用された特徴点を描く
for pointss in ptsCAM2i:
img2_a = cv2.circle(window_r, tuple(pointss), 5, (0, 255, 0), -1)
#座標軸を描く
cv2.line(img2_a, (25, 25), (int(25+R[0][0]*20), int(25-R[1][0]*20)), (255, 0, 0), thickness=1)
cv2.line(img2_a, (25, 25), (int(25+R[0][1]*20), int(25-R[1][1]*20)), (0, 255, 0), thickness=1)
cv2.line(img2_a, (25, 25), (int(25-R[0][2]*20), int(25-R[1][2]*20)), (0, 0, 255), thickness=1)
#角度を描く
img2_a = cv2.putText(img2_a, " alpha:{0:>8.3f}".format(alpha), (50,50), fontFace = cv2.FONT_HERSHEY_PLAIN, fontScale = 1.0, color = (0,0,255))
img2_a = cv2.putText(img2_a, " beta:{0:>8.3f}".format(beta), (50,70), fontFace = cv2.FONT_HERSHEY_PLAIN, fontScale = 1.0, color = (0,0,255))
img2_a = cv2.putText(img2_a, "gamma:{0:>8.3f}".format(gamma), (50,90), fontFace = cv2.FONT_HERSHEY_PLAIN, fontScale = 1.0, color = (0,0,255))
#画像2の表示と保存
cv2.imshow('img2_akaze',img2_a)
writer.write(img2_a) # 画像を1フレーム分として書き込み
##-----------------------------------------------------------------------------
# キー操作があればwhileループを抜ける
if cv2.waitKey(1) & 0xFF == ord('q'):
break
#ループ処理 ここまで
#------
# 終了処理
camera.release()
writer.release()
cv2.destroyAllWindows()
4. 説明
詳しい理論や計算式は、参照記事を確認ください。
1. 1フレーム目のカメラ方向を正面として計算
1フレーム目のカメラ方向に対して、2フレーム目以降がどれだけ回転してるかを求めました。
制約として、大きく回転しすぎてフレームに入る共通の特徴点が減ってくると計算できません。
2. 向きを示す行列 R の推定
エピポーラ幾何によると、$R$には2つの解がでて、どちらか決める必要があります。
これを決めるのに「2つの画像間で向きの変化は小さいはず。つまり単位行列$I$に近い」と仮定、トレース(=対角和)の絶対値が大きい方を解として選ぶようにしました。
3. 結果を画像表示
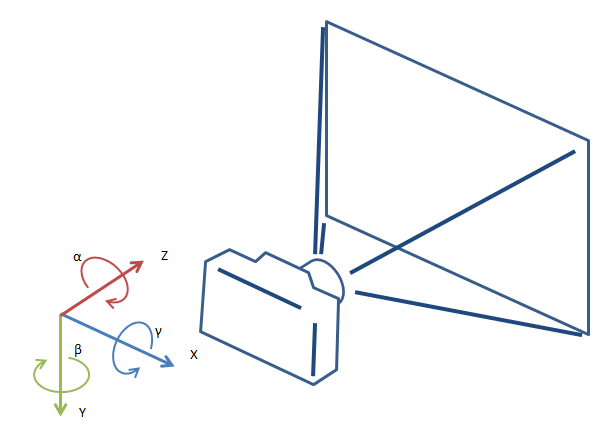
上図のように、カメラの向きで見て、座標系を「$X$:左$\rightarrow$右、$Y$:上$\rightarrow$下、$Z$:後$\rightarrow$前」」と定義し、それぞれの軸周りの回転を使って、向きを示す行列$R$を、
R = R_Z(\alpha)R_Y(\beta)R_X(\gamma)
と分解したときの角度$(\alpha, \beta, \gamma)$を表示しました。この計算の際にも「2つの画像の向きの変化が小さい」と仮定してます。
また、推定値のブレ具体が視覚的にわかるよう、軸方向を左上に表示しました。
5. 結果
テクスチャを貼った円柱を正面に配置し、各軸周りに首を振るCG動画で実行、左下のような
入力動画に対し右下のような出力結果になりました。


大体の方向を導き出してることがわかります。ブレは1度ほどでしょうか。
参考記事
特徴点抽出とマッチング)
https://qiita.com/tanaka_benkyo/items/5840a36d0e97a8498388
エピポーラ幾何)
https://daily-tech.hatenablog.com/entry/2019/07/14/150929
https://qiita.com/ykoga/items/14300e8cdf5aa7bd8d31
https://qiita.com/ssdsad/items/f5857c7774794a6e5f5e
https://tora-k.com/2020/06/25/findfundamentalmat/
https://buaiso.blogspot.com/2015/07/blog-post.html
https://brainsnacks.org/koyuu_tokui_bunkai/