もくじ
「画像から3次元データを復元する技術の調査 (1)概要」
https://qiita.com/akaiteto/items/caa8d64b1afd1fee7563
「画像から3次元データを復元する技術の調査 三次元座標の算出の原理 ~ステレオカメラによる三角測量~」
https://qiita.com/akaiteto/items/87e25c84647bb1e606ff
このシリーズについて
カメラをつかって三次元情報を復元する技術について調査したことを個人的な「勉強ノート」としてまとめる。
とくにMVSの処理に関心があるので、最終的にはMVSの各手法を原理レベルで記載したい。
そのうち点群操作系のアルゴリズムも勉強したい。
はじめに
曖昧な部分は原理レベルから調べることをモットーにページを作成した。
「三次元座標の算出の原理」では、単眼カメラとステレオカメラを対比させながら、
実際にどのようにして画像から三次元座標を算出するかを記載する。
「三次元座標の算出の原理」で説明する方法は2つ。
1つ、ステレオカメラを使った三角測量による手法。
2つ、単眼カメラによる複数視点の画像を用いたエピポーラ幾何による手法。
これらの手法の原理について、できるかぎり導出の部分を省かずに記載する。
加えて、コンピュータービジョンにおける基本的な知識である
内部パラメータ、外部パラメータ、射影行列、ピンホールカメラモデルについても説明し、
また、高校数学レベルから大学レベルまでの数学に関する基本的な知識についてもできるだけ説明した。
よって、本来は数ページに分けるところを一気に書いてあります。
「こんなもん書かなくてもわかる」のレベルから、
「大学のころやったけど曖昧だなぁ・・・」というレベルまで書いてるので
冗長な部分もあるとは思いますがご了承ください。(エピポーラ幾何はくそながいです・・・。)
構成
三次元座標の計算は大まかに下記のステップで行います。
このページでも下記の流れで説明しています。
0.エピポーラ幾何の概略
1.基本行列(essential matrix)の数式の導出
2.基礎行列(fundamental matrix)の数式の導出
3.基礎行列(fundamental matrix)の計算 ~8点アルゴリズム~
4.基本行列(essential matrix)から4つのカメラ姿勢(回転行列・並進行列)の抽出
5.三角測量(DLT)による三次元座標の推定・真なるカメラ姿勢の決定
前提

上図は、左と右、2つの視点から撮影された画像を図にしたものである。
$x_{L}$と$x_{R}$は同じ物体の同じ点を指していて、$X$はこれら2つの点が示す3次元座標である。
SfMと三角測量は、$x_{L}$と$x_{R}$が既知である前提知識のもとで$X$の算出が行われる。
よって、SfMと三角測量では2つの写真においてどのポイントが対応しているのかを把握しなければならない。
人間の目で見ればどこが同じであるかは明らかだが、計算機は計算してやらないとわからない。

したがって、計算機では最初の初期処理として「特徴点抽出」「特徴点マッチング」を行い、
2つの画像から$x_{L}$と$x_{R}$のような対応付けられたポイントを抽出する。
上記の画像は抽出した特徴点をマッチングさせた例である。
以降では、「特徴点抽出」「特徴点マッチング」により対応するポイントが
既知であるという前提のもと、説明を行うものとする。
なお、特徴点抽出と特徴点マッチングについては筆者が必要になった際に
別のページに記載するかもしれないししないかもしれないのでそちらを参照してください。
(1)エピポーラ幾何
三次元座標を算出できる原理の一つであるエピポーラ幾何について記載する。
(1-1)前提
単眼カメラによる復元では、不特定の多視点から撮影した画像をターゲットとする。
不特定な場所から自由気ままに撮影されているので、カメラの向きも間隔もバラバラである。
これを図にすると下記のような状態である。
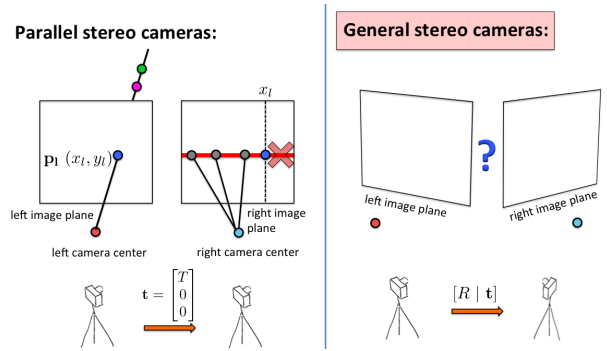
単眼カメラの場合は図の右に該当する。
ステレオカメラの場合は左の図に該当し、(1)にある通り非常にシンプルに解決することができた。
一方、右図。単眼カメラの場合はカメラの向きがバラバラに加えてカメラ同士の距離は未知数。
当然、三角測量と同じ条件は適用できない。別の考え方が必要である。
そこで役に立つのが「エピポーラ幾何」という原理。以下に細かく見ていく。
【参考】
http://www.cs.toronto.edu/~fidler/slides/2015/CSC420/lecture13_hres.pdf
(1-2)エピポーラ幾何の概略
エピポーラ幾何の概要のイメージを図で説明する。
図の$O$はカメラの位置。四角は映し出される画像平面、$p$は画像上の任意のピクセルである。
カメラが1つだけの状態は、片目をつぶってものを見たときと同じような状態である。
$p$の三次元座標を求めようとしたとき、片目をつぶると奥行きが分からなくなるのと同様に、
三次元座標の奥行きが定まらないので、候補となる座標が図のように直線$OP$上に連なる形となる。

次に右から見た画像を追加してみる。候補点を追加した画像に逆射影し、
これらの三次元座標が右の画像上ではどこに映し出されるか、右の画像上にプロットしてみる。
すると図の通り、三次元座標と画像のポイントが点線で結びつく5つの組ができた。
これらの特徴の一つとして、画像上に映し出した候補点が「直線」に連なっているところがポイントである。
さて、この5つの組のいずれかが
左の画像の黒いポイントにとっての正解となるはずである。どれが正解だろう?
実はこの答えをすでに我々は知っている。
このページの最初の前提の項で説明したとおり、特徴点マッチングにより
ある画像のポイントが別の画像のどのポイントと対応づくかを把握済みである。
図でいえば、青い点と黒い点が対応するポイントである。
これらの点が結びつく3次元座標が正解の座標。
よって、それぞれのカメラの視点と青と黒の点を結んだ三次元座標が求めたい座標となる。
以上が、エピポーラ幾何における基本的な考え方である。
(1-3)概略から詳細へ
次のステップとしては、この考えを数式で表しコーディングに落とし込まなければならない。
用語で以降の処理をいきなり説明するなら、
「エピポーラ幾何より基本行列と基礎行列を求めて、カメラ姿勢を推定し、
そこから射影行列を求めることで三次元座標を取得する。」である。
しょっぱなから基本行列と基礎行列の関係式を提示してもよいが、
それだとどうにもわかりにくいので以降では、基本行列・基礎行列の導出をできるだけ丁寧に記載し、
高校数学レベルでもわかるように説明を行うことを目標としたい。
そのためにもまずは基本知識の説明である。
基本知識1~3にて、内積・外積の知識と回転行列・移動行列について説明する。
知っている人は読み飛ばしてもらって構わない。
【参考】
https://github.com/openMVG/openMVG
Multiple view geometry in computer vision. Hartley, Richard, and Andrew Zisserman. Vol. 2. Cambridge,
2000.(P281 seven point correspondences)
https://web.stanford.edu/class/cs231a/course_notes/03-epipolar-geometry.pdf
基礎知識1 直角の内積
まずは高校数学を復習する。
直角をなすベクトルの内積が0になることを覚えているだろうか。

参考:http://www.geisya.or.jp/~mwm48961/kou2/vector_para_ortho.html
内積の公式は$\overrightarrow{a}・\overrightarrow{b}=|a||b|cosθ$。
θは$\overrightarrow{a}$と$\overrightarrow{b}$のベクトルがなす角度であり、
90度の場合はcos90=0よりこの時の内積は必ず0となる。
この条件を任意の平面に対して適用させてみる。
下記の図のように、平面上にある任意のベクトルと、その平面に垂直な法線ベクトルは必ず90度の関係になる。
よって、平面においては必ず下記の式が成立する。
$\boldsymbol{(平面のベクトル)}・\boldsymbol{(平面の法線ベクトル)}=0$
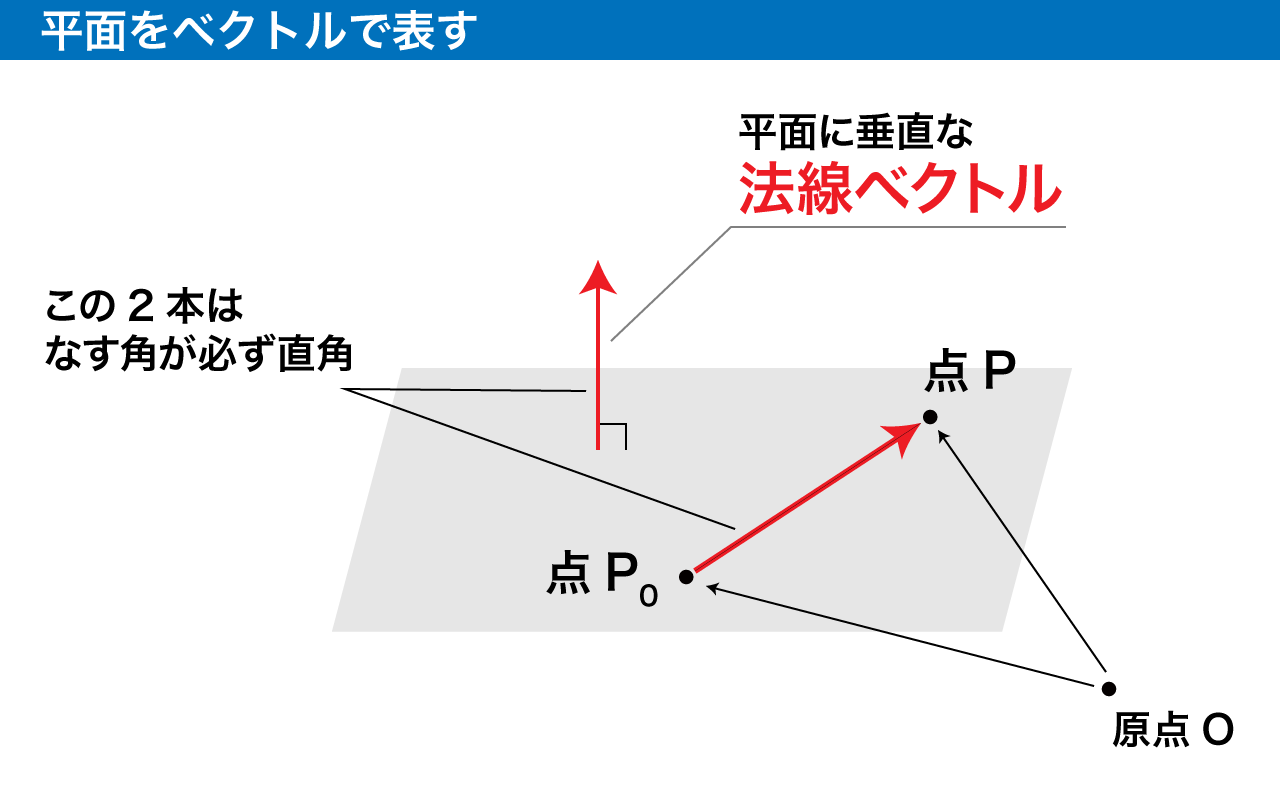
参考:https://oguemon.com/study/linear-algebra/vector-figure/
基礎知識2 外積
それでは平面ベクトルから法線ベクトルを求めるにはどうすればよいか。
平面の法線ベクトルは外積でもって表現することが可能である。
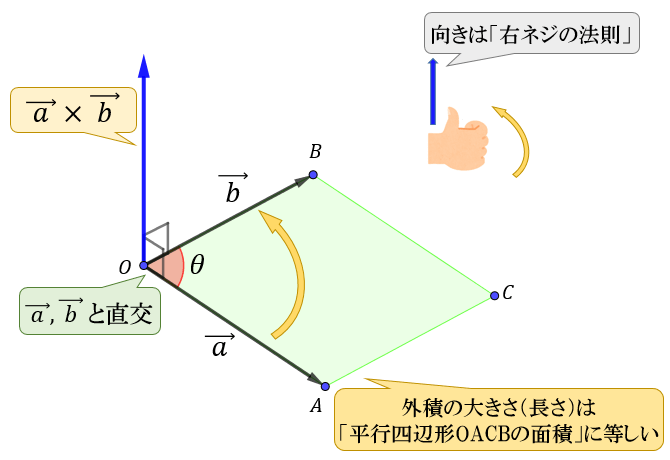
参考:https://atarimae.biz/archives/23716
$\boldsymbol{a}×\boldsymbol{b}=(aとbがなす平面の法線ベクトル)$
したがって、(1-3)(1-4)をまとめると以下のような式が導かれる。
$\boldsymbol{(平面のベクトル)}・\boldsymbol{(平面の法線ベクトル)}=0$
$ ⇒ \boldsymbol{(平面のベクトル)}・\boldsymbol{(平面の2つのベクトルの外積)}=0$
基礎知識2 回転行列について
さて本題・・・の前に、計算機における画像の扱いについて触れる。
多視点の画像を取扱う分野において、
とある事情(後述)により画像を回転させたり移動させたりすることが必要になる。
画像を回転させる方法について、二次元空間と三次元空間に分けて説明する。
まずは二次元上で画像の回転。
画像を二次元平面に映し出すと、画像の各ピクセルは二次元座標であらわされる。
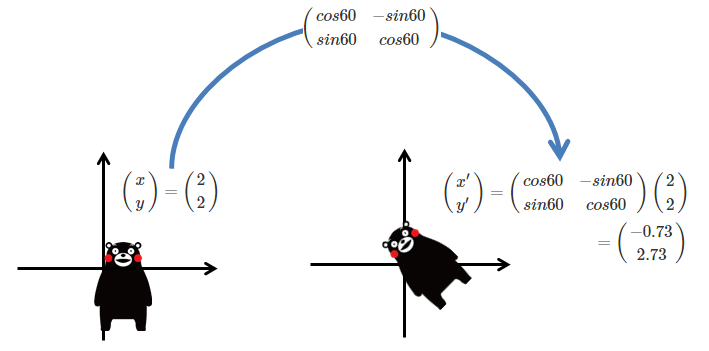
下記の画像でいえば、クマモンの鼻は図では(2,2)に位置している。
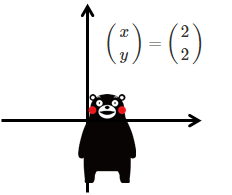
この画像を回転させようと思ったとき、「回転行列」なるものを用いれば簡単に回転させられる。
回転角度$Θ$、(x、y)を回転前、(x',y')を回転後の座標とすれば、行列は下記のようになる。
\left(
\begin{array}{c}
x'\\
y'
\end{array}
\right)
=
\left(
\begin{array}{cc}
cosΘ & -sinΘ\\
sinΘ & cosΘ
\end{array}
\right)
\left(
\begin{array}{c}
x\\
y
\end{array}
\right)
三角関数を内包している行列を、回転行列とよぶ。回転させたい角度さえ分かれば簡単に回転させられる便利な行列である。
この式を実際に使用して、先ほどのクマモンを60度回転させてみると以下のようになる。
図では、鼻の部分のピクセルの計算について特に行っているが、
実際には画像のすべてのピクセルに対して同様の計算を行う。
これにより、二次元平面において画像を回転することができた。
ではこれが三次元座標の場合はどのように回転させるのだろう。
画像を三次元座標で回転させる場合、x,y,z軸それぞれに対する回転が発生する。
よって回転行列はさきほどのものにZ軸が加わって以下のようにあらわされる。
x,y,z軸の回転角度をα、β、γとすると以下の式となる。
\left(
\begin{array}{ccc}
u\\
v\\
w
\end{array}
\right)
=
\left(
\begin{array}{ccc}
cosαcosβ & -cosβsinα & sinβ\\
cosγsinα+cosαsinβsinγ & cosαcosγ-sinαsinβsinγ & -cosβsinγ\\
sinαsinγ-cosαcosγsinβ & cosγsinαsinβ+cosαsinγ & cosβcosγ\\
\end{array}
\right)
\left(
\begin{array}{ccc}
u'\\
v'\\
w'
\end{array}
\right)
これを三次元空間の画像に対して実行すると、以下のようなイメージで回転する。

(画像間違ていました。$X^R=RX$です)
三次元空間において、画像の向く面が変わるようなイメージで回転が行われる。
面の向きを揃えたい時などにとても有効である。
以上が回転行列の概要である。
基礎知識3 移動行列について
次に移動行列について考える。
移動行列は至ってシンプル。回転行列では取り扱う次元によって若干式が異なったが、
移動行列は次元に関係なく各軸の移動量をそのまま足し算するだけである。
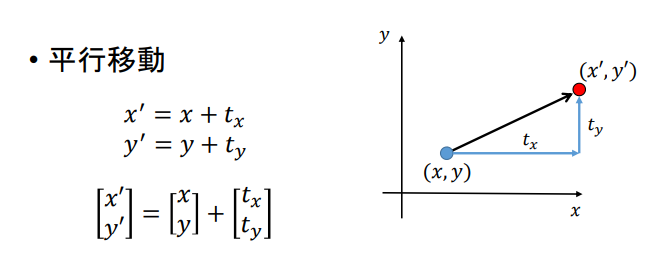
【参考】
http://mitani.cs.tsukuba.ac.jp/lecture/2019/cg_basics/02/02_slides.pdf
(2)基本行列(essential matrix)の数式の導出
(2-1)はじめに
基本知識は以上。ここから先はエピポーラ幾何に基づく説明。
三角測量では図形から方程式を導出することで座標の計算を行った。
同じように、エピポーラ幾何でも方程式を導出する。
 上図は(1-2)で示した画像である。
この図は概念図でしかないので、(1-2)の図をベクトルで表現してみる。
上図は(1-2)で示した画像である。
この図は概念図でしかないので、(1-2)の図をベクトルで表現してみる。
【参考】
http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/EPSRC_SSAZ/node21.html
https://web.stanford.edu/class/cs231a/course_notes/03-epipolar-geometry.pdf
(2-2)左のカメラをベクトル空間に表してみる
 図は左のカメラが撮影する様子をx,y,z軸のユークリッド空間で図にしたもの。
$O$はカメラの位置であり、この座標系の原点。
青く着色された平面はカメラが画像を映し出す面。$X$は(1-2)の図の黒い点と思ってほしい。
なお、このようにカメラの位置を原点とした座標系をカメラ座標と呼ぶ。
図は左のカメラが撮影する様子をx,y,z軸のユークリッド空間で図にしたもの。
$O$はカメラの位置であり、この座標系の原点。
青く着色された平面はカメラが画像を映し出す面。$X$は(1-2)の図の黒い点と思ってほしい。
なお、このようにカメラの位置を原点とした座標系をカメラ座標と呼ぶ。
左のカメラを回転させる
カメラが1つしか表わせていないので、これだけでは(1-2)を表現したとは言えない。
次は左のカメラを移動させて右のカメラも表現してみる。
まずは向き。2つのカメラはそれぞれ向きが異なっていた。
回転行列$R$分だけ右と左で角度が違っていると仮定して、
$R$を用いることで左カメラに映し出される画像面を右カメラと同じ向きに回転させる。

これにより、右のカメラの向きだけは表現できた。
左のカメラを移動させる
次は位置。
右カメラは位置が大きく離れているので移動させる。
右と左のカメラは移動行列$T$だけ離れていると仮定して、移動行列を足し合わせ移動させる。

以上より、左のカメラを回転・移動させることで右カメラを疑似的に表現できた。
左のカメラを回転・移動させたことによって・・・
 右の画像面にあるポイント$X_{RT}$は(1-2)の図でいう青い点、
左の画像面にあるポイント$X$は(1-2)の図でいう黒い点である。
これにより2つのカメラが存在する空間を表現することができた。
右の画像面にあるポイント$X_{RT}$は(1-2)の図でいう青い点、
左の画像面にあるポイント$X$は(1-2)の図でいう黒い点である。
これにより2つのカメラが存在する空間を表現することができた。
ここまでの長ったらしいくどい説明を行ったのは、以下の関係式を手に入れるためである。
$X_{RT}=RX+T$
この式は後の工程でとても重要な役割を果たす。
なお余談だが、このようにカメラ$O$を座標の原点とした座標系のことをカメラ座標と呼ぶ。
(2-2)方程式を導き出す
結論から言えば、下記の図の直角の関係を利用することで方程式を導くことができる。
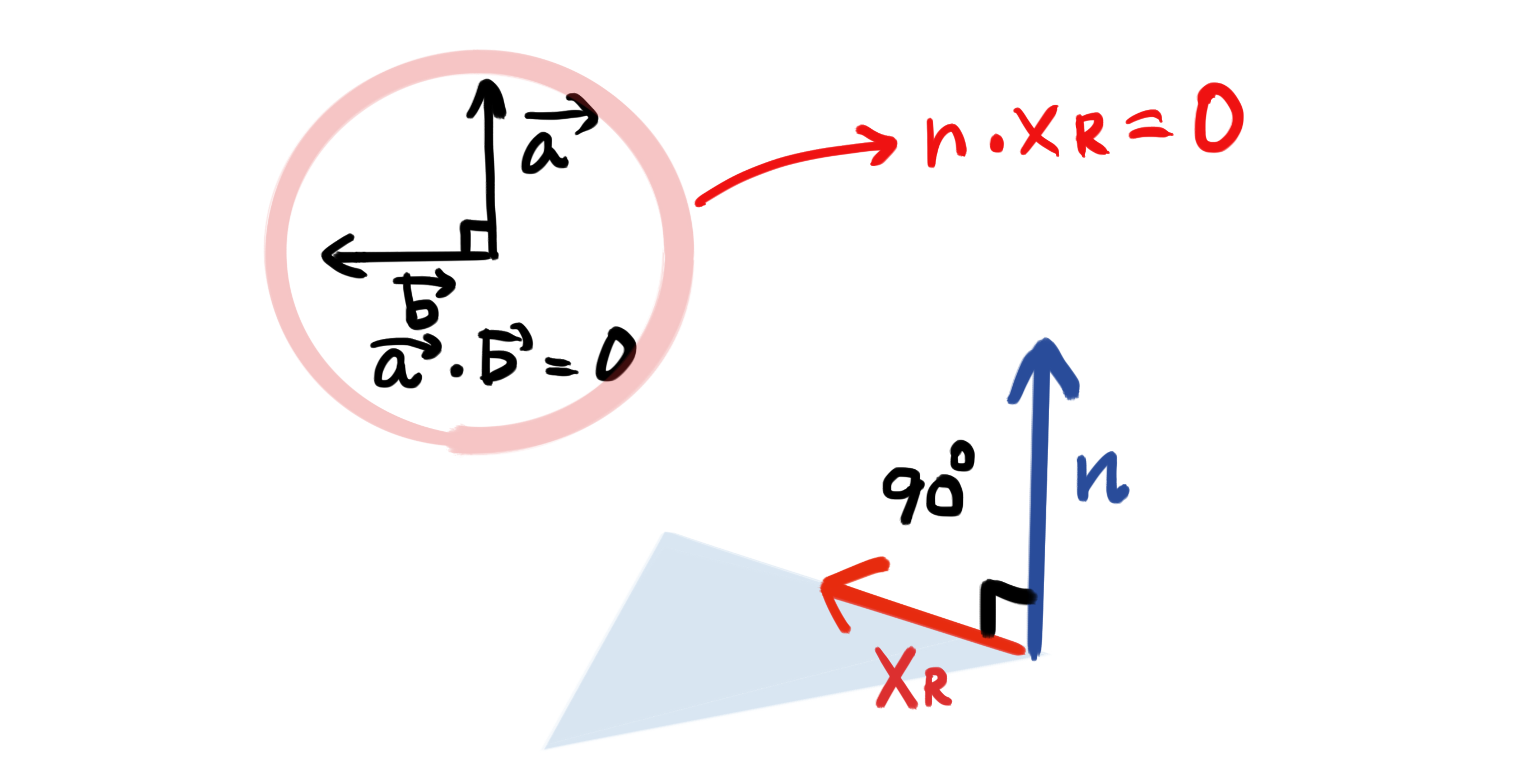
$\boldsymbol{X_{R}}$ ・・・・ 右のカメラの位置から、画像のポイントまでのベクトル。
(1-2)で言う青いポイントを指すベクトルである。
$\boldsymbol{X_{R}}$は右のカメラのカメラ座標系を基準としたベクトルでもある。
$\boldsymbol{n}$・・・・・・三次元座標と左右2つのカメラの位置を結んだ三角形の平面に対して、直角の法線ベクトル。
${X_{R}}$と${n}$は直角の関係。よって内積は0になるので方程式は以下のようになる。
(※内積が0になる理由については「(1-3)基礎知識1 直角の内積」を参照)
$X_{R} \cdot n=0$
この方程式こそがエピポーラ幾何における最重要な式である。
ここまでの知識を用いて${X_{R}}$と${n}$の中身を数式でより具体化させていく。
導出1 [Xr]の導出
$\boldsymbol{X_{R}}$を図に示すと以下のようになる。

先ほど導出した$X_{RT}=RX+T$と、移動させる際に使用した$T$より、
$\boldsymbol{X_{R}}=\boldsymbol{(RX+T)-T}=\boldsymbol{RX}$が求まる。
(※図の画像が誤字ってます・・・。${X_{L}}$は$X$と思ってください。)
導出2 [n]の導出
 移動行列$T$と$\boldsymbol{X_{R}}$のなす平面に対する法線ベクトル$\boldsymbol{n}$は、
先ほど求めた$\boldsymbol{X_{R}}=\boldsymbol{RX}$を利用すると以下のようになる。
移動行列$T$と$\boldsymbol{X_{R}}$のなす平面に対する法線ベクトル$\boldsymbol{n}$は、
先ほど求めた$\boldsymbol{X_{R}}=\boldsymbol{RX}$を利用すると以下のようになる。
$\boldsymbol{n=T×X_{R}=T×RX}$
(※図の画像が誤字ってます・・・。${X_{L}}$は$X$と思ってください。)
(※外積については「(1-4)基礎知識2 外積」を参照)
(2-3)基本行列(Essential Matrix)の導出
そして導出した$\boldsymbol{n}$を内積の式に当てはめて整理する。
わかりづらいので書く計算過程ごとに説明する。
X_{R} \cdot n = X_{R} \cdot (T×RX)-----(1)\\
X_{R} \cdot n = X_{R}^{t}(T×RX)-----(2)\\
X_{R} \cdot n = X_{R}^{t}(T×R)X-----(3)\\
X_{R} \cdot n = X_{R}^{t}EX\\
★(1)について
$\boldsymbol{n}$に導出した式を当てはめただけ。
ここまでの説明で$X_{R}$の式も導出したが、後々のために$X_{R}$は残しておく。
★(2)について
ここの変換がややこしい。
内積と乗算の違いを忘れていると混乱するはめにあう(私です)。
$X_{R}^{t}$の右上にある$t$はベクトルの転置行列を表している。
変換の詳しい説明と合わせて。転置行列の意味と内積について以下に説明する。
仮にここにベクトルa,bがあったとする。
a=\left(
\begin{array}{ccc}
a_{1}\\
a_{2}\\
a_{3}
\end{array}
\right)
\\
b=\left(
\begin{array}{ccc}
b_{1}\\
b_{2}\\
b_{3}
\end{array}
\right)
\\
まずは基本知識の確認。
$a$と$b$の内積は以下の様に計算される。
a \cdot b = a_{1}b_{1}+ a_{2}b_{2}+ a_{3}b_{3}
ちなみに「$\cdot$」は2・2=4のように乗算にも使われる記号だがベクトルにおいては意味が異なる。
「$\cdot$」は内積を意味する記号であって、乗算とは全く別物である。
乗算はベクトルだが、内積は2,3などのその辺の数字(スカラー)であり。
マリカーのプロゲーマーと、本物のレーサーくらいに戦う分野が違うので注意する。
ついでに言うと、外積は「×」で表されるが乗算とは違う意味である。なんとわかりにくいことか。
内積:
a \cdot b = a_{1}b_{1}+ a_{2}b_{2}+ a_{3}b_{3}
乗算:
sb=
\left(
\begin{array}{c}
s_{1} & s_{2} &s_{3}
\end{array}
\right)
\left(
\begin{array}{ccc}
b_{1} \\
b_{2} \\
b_{3}
\end{array}
\right)
=
\left(
\begin{array}{ccc}
s_{1}b_{1} \\
s_{2}b_{2} \\
s_{3}b_{3}
\end{array}
\right)
外積:
s×b=
\left(
\begin{array}{c}
s_{1} & s_{2} &s_{3}
\end{array}
\right)
×
\left(
\begin{array}{ccc}
b_{1} \\
b_{2} \\
b_{3}
\end{array}
\right)
=
\left(
\begin{array}{ccc}
s_{2}b_{3} -s_{3}b_{2} \\
s_{3}b_{1} -s_{1}b_{3} \\
s_{1}b_{2} -s_{2}b_{1}
\end{array}
\right)
次に転置行列。今回初めて出てきた概念である。
転置行列は縦横が入れ替わるだけなので、転置行列$a^{t}$は下記のようになる。
a^{t}=\left(
\begin{array}{c}
a_{1} & a_{2} &a_{3}
\end{array}
\right)
さて次が一番説明したかったこと。
転置行列と内積の関係式は以下のようにあらわせる。
a^{t}b
=
\left(
\begin{array}{c}
a_{1} & a_{2} &a_{3}
\end{array}
\right)
\left(
\begin{array}{ccc}
b_{1}\\
b_{2}\\
b_{3}
\end{array}
\right)
=
\left(
a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}
\right)=
a \cdot b\\\\
⇔\\\\
a^{t}b=a \cdot b
$a^{t}b=a \cdot b$これこそが知りたかった関係式。
これをさきほどの内積の右辺に当てはめることで、(2)の式になる。
★(3)について
カッコをたしただけ。
以上の(1)~(3)より、最終的には以下の等式が導かれる。
$X_{R}^{t}EX=0$
ここでいう$E$は以下の式であらわされる。
$E=T×R$
$E$の行列を「基礎行列」と呼ぶ。
英語でいうとessential matrix。直訳で「必要不可欠な行列」である。
着目すべき点は、基礎行列$E$が2つのカメラの位置関係、$R$と$T$の行列を内包している点である。
基礎行列が表現するもの、それはカメラ同士がどれくらい向きが違っていて、
どれくらい移動しているかというカメラの位置関係である。
これがもーーーー本当に大切。エピポーラ幾何のすべてといっても過言ではない。
以降は実際に基礎行列$E$を利用してみる。
(3)基礎行列(fundamental matrix)の数式の導出・・・の前に
(3-1)はじめに
$X_{R}^{t}EX=0$という方程式の導出に成功した。
実は、この$E$さえわかれば三次元座標が計算し放題なのである。
用語でいえば、$E$が判明することにより射影行列が求められる。
射影行列というものは、画像のピクセルの二次元座標をダイレクトに三次元座標に変換できるめちゃスゴスーパー行列である。
$E$さえ求めれば証明終了。早急に$E$を利用したいが、
現時点ではまだ$E$がどのような値を持つかわかっていない。
以降では、まずは$E$を求めることにフォーカスを充てる。
最初の方針
ということで$E$を求めたい。
$X_{R}^{t}EX=0$の方程式をうまく使えば$E$が求められるはず。
基礎行列$E$の式において、何が既知で何が不明なのかを整理し方針を決める。
$X_{R}^{t}EX=0$
【$E$について】
さっぱりわからない。$E$の中身はカメラの位置と姿勢だが、
手元にあるのは不特定の場所から撮影された画像だけ。今のところ判別不能である。
(・・・と書いたが、実は$E$単体を求めることも可能である。しかしここでは定石通りの流れで導出する。)
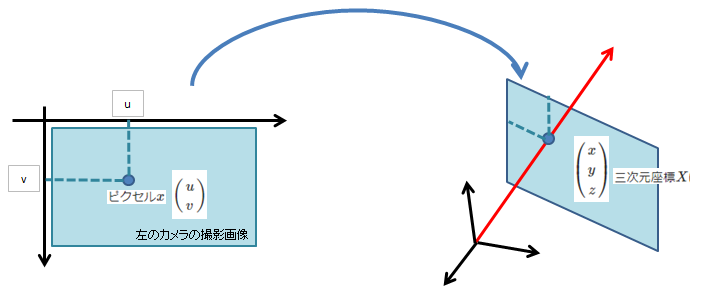
【$X$と$X_{R}$について】
$X$は下図にあるように、カメラの撮影位置からポイントXまでの三次元座標である。

$X$は今までの説明でも何度も登場したし、$X$のもとになる特徴点は簡単に求められる。
なんとなーく$X$と$X_{R}$ならわかる気がしてくる。
それでは$X$と$X_{R}$は具体的にどんな値だろう?
・・・しかし残念なことに現時点までの情報だけでは、$X$と$X_{R}$の具体的な値はわからない。
求めたいのは三次元空間における$X$と$X_{R}$の三次元座標。
しかし今の時点で既知である情報は2つの特徴点がマッチングしている情報だけ。
厳密に言えば、左の画像のピクセル$x$の座標$(u,v)$が、右の画像のピクセル$x'$の座標$(a,b)$と
マッチングしていることしかわからない。
よって、$E$を求めるにあたってまず行わなければならないことは、
ピクセル$x$を三次元座標$X$に変換する方法を見つけること、
すなわち、画像座標をカメラ座標に変換する方法の発見である。
(3-2) カメラの内部パラメータKの導出(intrinsic parameters)
クマモンを例に考える。

画像の赤い点のピクセルの座標を何気なく$(u,v)$と記載したが、これは画像の左上を原点とした場合の座標である。
ただ、図のように左上が原点であると、後の説明で少し都合が悪いので別の座標軸を考える。

上図の右のように画像の中心に原点を置いて$(u',v')$とする。以降では下の図の右を中心に説明する。
なお、画像の中心を主点(principal point)と呼ぶ。
そしてこれらの図をXYZの三次元空間に表示する。
原点はカメラの位置に配置しカメラ座標を想定する。
ここでは、XY軸は画像空間に平行、かつZ軸がカメラの主点を貫く軸を想定していることに注意されたい。
上図の三次元空間を別の視点で下記のように図で示した
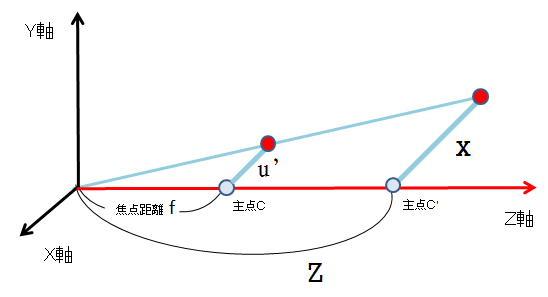
図に引かれた青い線は互いに平行であるので、三角形の相似の関係より下記の式が導かれる。
\frac{u'}{f} = \frac{X}{Z}\\
u' = f\frac{X}{Z}
これにより、二次元のピクセル座標のX座標$u'$が三次元座標$(X,Y,Z)$であらわされた。
同様に、$v'$についても式で表すと以下の2式が手に入る。
\left\{
\begin{array}{ll}
u' = f\frac{X}{Z}\\
v' = f\frac{Y}{Z}
\end{array}
\right.
さらに変形。
\left\{
\begin{array}{ll}
Zu' = fX\\
Zv' = fY
\end{array}
\right.
この2つの式を行列にしたものが下記。
Z
\left(
\begin{array}{ccc}
u'\\
v'
\end{array}
\right)
=
\left(
\begin{array}{cc}
f & 0\\
0 & f
\end{array}
\right)
\left(
\begin{array}{cc}
X\\
Y
\end{array}
\right)
先ほどは「ピクセルを三次元座標に変換する方法を見つける」ことを目標として掲げた。
上記の式は三次元座標のうちXY座標は求められるがZ軸は不明のままである。
よってさきほどの方程式に下記の式を追加して、再度行列を表現する。このような座標の表現を「同次座標」と呼ぶ。
\left\{
\begin{array}{ll}
Zu' = fX\\
Zv' = fY\\
Z=Z
\end{array}
\right.
⇔
Z
\left(
\begin{array}{ccc}
u'\\
v'\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & 0\\
0 & f & 0\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)
$(u',v')$は画像の主点を原点としたときの座標である。
画像座標の一般的な原点は画像の左上の位置である。主点が原点はあまり一般的ではないので、座標の軸を移動させる。
左上を原点として$u,v$軸で表すと式は以下のように変換される。
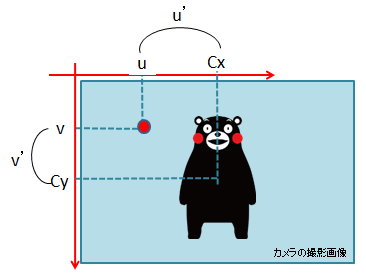
\left\{
\begin{array}{ll}
u'=u-C_{x}\\
v'=v-C_{y}\\
\end{array}
\right.
⇔
\left(
\begin{array}{cc}
u'\\
v'
\end{array}
\right)
=
\left(
\begin{array}{cc}
u-C_{x}\\
v-C_{y}
\end{array}
\right)
これを先ほどの式に反映させる。
\left\{
\begin{array}{ll}
Zu = ZC_{x}+fX\\
Zv = ZC_{y}+fY\\
Z=Z
\end{array}
\right.
⇔
Z
\left(
\begin{array}{ccc}
u\\
v\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)
\\
⇔
s
\left(
\begin{array}{ccc}
u\\
v\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)\\
これにより、画像座標をカメラ座標に変換する式が産出できた。
(なお、最終的な式としてs=Zに置き換えて記載した。このsをスケールファクタと呼ぶ。)
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
上記の行列が画像座標をカメラ座標に変換する変換行列。これを用語で内部パラメータと呼ぶ。
加えて、ピンホールカメラでこのように表されたモデルをピンホールカメラモデルとも呼ぶ。
なお、この項では焦点距離を$f$として扱ったが、人によっては$f_{x},f_{y}$と記載する場合がある。
これはいわゆるアスペクト比であり、焦点距離は像のスケールを決定させるものなので、
$f_{x},f_{y}$のようにx、yでそれぞれスケールを分けることにより、
画像のアスペクト比の横縦の比率を変えたりすることができる。
※余談
上記では、座標の軸を主点から画像左上に移動させる際に、方程式にしてから行列を導いた。
実はこんなことをしなくとも、この式は同次座標とよばれるもので表現されているため、
もっと簡単に表すことができる。
以降の説明の中で基本知識として同次座標について触れているので、
その項を参照してください。
【参考】
https://ja.coursera.org/lecture/robotics-perception/pinhole-camera-model-wKcXj
https://ja.coursera.org/lecture/robotics-perception/intrinsic-camera-parameter-6IISZ
https://vislab.jp/hiura/lec/iip/geometry2013.print.pdf
(3-3)基礎行列の算出の前準備
さきほどは内部パラメータによって画像座標をカメラ座標に変換することに成功した。
$X$と$X_{R}$はカメラ座標で表された三次元座標であるので、内部パラメータで表すことが可能である。
まずは、スケールファクタ$s$=1として内部パラメータの式を整理する。
\left(
\begin{array}{ccc}
u\\
v\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)\\
上式は画像座標$(u,v)$に関する式なので、左辺にカメラ座標$(X,Y,Z)$が来るように変形しなければならない。
実際に変形する前に、軽くベクトル復習する。逆行列・単位行列・転置行列を覚えている人は読み飛ばしてください。
基本知識4 逆行列・単位行列
高校数学にも出てくる逆行列、単位行列というものを覚えているだろうか。
逆行列は$A^{-1}$と表記される。左上に「-1」がついたものを逆行列と呼ぶ。
性質としては、ベクトル$A$を打ち消すような働きをする。
実際の数値で示すと、下記のような作用になる。
A \cdot A^{-1}
=
\left(
\begin{array}{ccc}
2 & 5\\
1 & 3
\end{array}
\right)
\left(
\begin{array}{ccc}
3 & -5\\
-1 & 2
\end{array}
\right)
=
\left(
\begin{array}{ccc}
1 & 0\\
0 & 1
\end{array}
\right)
=I
対角線に1と0がならぶ行列を単位行列$I$と呼ぶ。
とあるベクトルの逆行列をそのベクトルに掛け合わせると、単位行列が生まれる。
次に単位行列の性質についてみてみる。以下の式より、単位行列は掛け合わせても何も影響を与えないことがわかる。
A \cdot I
=
\left(
\begin{array}{ccc}
2 & 5\\
1 & 3
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0\\
0 & 1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
2 & 5\\
1 & 3
\end{array}
\right)
=A
次にこれらを活用して、$U=KX$の式を$X$の形に変更してみる。
まずは$U=KX$に対して$K^{-1}$を左から掛け合わせてみる。
$\boldsymbol{K^{-1}U=K^{-1}KX}$
$A \cdot A^{-1}=I$の関係式より、
$\boldsymbol{K^{-1}U=IX}$
$A \cdot I=A$の関係式より、
$\boldsymbol{K^{-1}U=X}$
最後に右辺左辺を交換。
$\boldsymbol{X=K^{-1}U}$
よって、$U$の式を$X$に関する式に変更することができた。
基本知識5 転置行列と逆行列
転置行列は基礎行列にて触れた概念だが改めてもう一度式にしてみる。
a=\left(
\begin{array}{ccc}
a_{1}\\
a_{2}\\
a_{3}
\end{array}
\right)
\\
a^{t}=\left(
\begin{array}{c}
a_{1} & a_{2} &a_{3}
\end{array}
\right)
転置行列は単純に縦横が入れ替わった行列。
証明は省くが、転置行列には以下の性質がある。
$(AB)^{t}=B^{t}A^{t}$
この性質を利用して、$(A^{-1}B)^{t}$を変換してみる。
$\boldsymbol{(A^{-1}B)^{t}=(B^{t}(A^{-1})^{t})}$
$\boldsymbol{(A^{-1}B)^{t}=B^{t}A^{-t}}$
(4)基礎行列(fundamental matrix)の数式の導出
ということで、ここまでの基本知識をつかって$X_{R}^{t}EX=0$を整理する。
さきほどまでの話では、$X$,$X_{R}$がピクセル座標で表せないことが問題であった。
基本知識4より、内部パラメータの式を変形させる。
\left(
\begin{array}{ccc}
u\\
v\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)\\
⇔
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)^{-1}
\left(
\begin{array}{ccc}
u\\
v\\
1
\end{array}
\right)\\
上記の式だと長いので、$(u,v,1)$を画像座標$m$。三次元座標$(X,Y,Z)$を$M$、内部パラメータを$K$とすると
M=K^{-1}m
これにより、$X$と$X_{R}$をピクセルであらわすことができる 。
この式の$M$に$X$と$X_{R}$を当てはめ、$X_{R}^{t}EX=0$を変形させる。
X_{R}^{t}EX=0\\
⇔\\
(K^{-1}p_{l})^{t} E K^{-1}p_{r}=0\\
次に基本知識5を当てはめる。
X_{R}^{t}EX=0\\
⇔\\
p_{l}^{t}K^{-t}E K^{-1}p_{r}=0\\
$F=K^{-t}E K^{-1}$とすると、最終的に以下の式となる。
p_{l}^{t}Fp_{r}=0
これこそがエピポーラ拘束式と呼ばれるもの。$F$を基本行列(Fundamental Matrix)と呼ぶ。
この式こそがエピポーラ幾何において一番求めたかった式である。
(4-1)基礎行列Fはどんな行列?
ここまでの方針の流れをまとめると下記の通り。
①「基礎行$E$がわかれば、三次元座標がわかる!」
↓
②「$F$がわかれば、$E$がわかる!」
↓
③「$X$と$X_{R}$がわかれば、$F$がわかる!」
↓
④「画像のピクセルの座標がわかれば、$X$と$X_{R}$がわかる!」←いまここ
現在は4のステップ。画像のピクセルはもちろん既知である。
ついに、ようやく、答えを導き出すことができる・・・!
ということで、$X$と$X_{R}$に対応するピクセルの座標より、③のステップで$F$を計算してみよう。
p_{l}^{t}Fp_{r}=0
左の画像のピクセル座標を$(u,v)$、右の画像のピクセル座標を$(a,b)$として式に代入する。
\left(
\begin{array}{c}
u & v & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
F_{11} & F_{12} & F_{13} \\
F_{21} & F_{22} & F_{23} \\
F_{31} & F_{32} & F_{33}
\end{array}
\right)
\left(
\begin{array}{ccc}
a \\
b \\
1
\end{array}
\right)
=
0
左の二つの行列を展開する。
\\
\left(
\begin{array}{c}
uF_{11}+vF_{21}+F_{31} && uF_{12}+vF_{22}+F_{32} && uF_{13}+vF_{23}+F_{33}
\end{array}
\right)
\left(
\begin{array}{ccc}
a \\
b \\
1
\end{array}
\right)
=
0
\\
auF_{11}+avF_{21}+aF_{31}+buF_{12}+bvF_{22}+bF_{32}+uF_{13}+vF_{23}+F_{33}=0
展開された式を再び行列にする。(ここがピンとこない人は下記の式を展開してみてください。)
\left(
\begin{array}{c}
au & av & a & bu & bv & b & u & v & 1
\end{array}
\right)
\left(
\begin{array}{ccccccccc}
F_{11}\\
F_{12}\\
F_{13}\\
F_{21}\\
F_{22}\\
F_{23}\\
F_{31}\\
F_{32}\\
F_{33}
\end{array}
\right)
=0
仮にここで。左の画像のピクセル座標を$(u,v)=(2,2)$、右の画像のピクセル座標を$(a,b)=(1,1)$の組と、
左の画像のピクセル座標を$(u,v)=(1,1)$、右の画像のピクセル座標を$(a,b)=(2,2)$の組。
これら2つの特徴点のマッチングがわかっていたとすれば、先ほどの行列式より以下の2つの方程式が求まる。
2F_{11}+2F_{12}+2F_{13}+2F_{21}+2F_{22}+1F_{23}+F_{31}+F_{32}+F_{33}=0\\
2F_{11}+2F_{12}+F_{13}+2F_{21}+2F_{22}+F_{23}+2F_{31}+2F_{32}+F_{33}=0
中学生の連立方程式では、2つの変数があるときは2つの方程式があれば解くことができたが、
$F$の場合はいくつの方程式が必要になるだろう。
とりあえず以下に、n個の方程式があるときの式を行列に表した。
\left(
\begin{array}{c}
a_{1}u_{1} & a_{1}v_{1} & a_{1} & b_{1}u_{1} & b_{1}v_{1} & b_{1} & u_{1} & v_{1} & 1 \\
a_{2}u_{2} & a_{2}v_{2} & a_{2} & b_{2}u_{2} & b_{2}v_{2} & b_{2} & u_{2} & v_{2} & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
a_{n}u_{n} & a_{n}v_{n} & a_{n} & b_{n}u_{n} & b_{n}v_{n} & b_{n} & u_{n} & v_{n} & 1
\end{array}
\right)
\left(
\begin{array}{ccccccccc}
F_{11}\\
F_{12}\\
F_{13}\\
F_{21}\\
F_{22}\\
F_{23}\\
F_{31}\\
F_{32}\\
F_{33}
\end{array}
\right)
=0
中学の式であれば、連立方程式は、変数の数分だけ方程式があれば解くことができるはず。
$F$の場合は変数が9個なので、今作成した方程式も加えて合計9個の特徴点の組より
9個の方程式を作れば解くことができる・・・というのが、中学生までの知識。
大学生レベルになると実際のデータを扱うので、
「そもそもこの連立方程式でとけるの?」というところから考えないといけない。
実際のデータにはノイズ等による外れ値が存在し、間違った方程式が混ざることが起こり得る。
例えばもしも、以下のような連立方程式があったとして、中学知識で2つの式を引き算すると、
1=2という矛盾が発生する。このような場合はそもそも解を求めることができない。
\left\{
\begin{array}{lll}
x+y+2z=1\\
x+y+2z=2
\end{array}
\right.
\\
⇔
\\
1=2
$F$の式に関して言えば、選んだ特徴点の組の中で見当違いなものがあれば、
間違った方程式が混ざり合ってしまい、同じように解がそもそも求まらないことも起こり得る。
解は1つに求まるのか、あるいは解は無限か、そもそも求まらないか。
これらは実は、方程式から判断することが可能である。
以降にその方法について詳しく見てみる。
基本知識6 行列のランクと自由度
ランク(階層)について説明する。
\left\{
\begin{array}{lll}
x+y+z=1\\
x+2y+z=2\\
x+y+z=2
\end{array}
\right.
例として、上記の連立方程式を考える。
この連立方程式をよく見ると、1式目と3式目が明らかに矛盾している。
この連立方程式を満たす解は絶対に存在しないことが直感的にわかる。
このような判断を機械的に行えるのがrank(階数)という考え方である。
まずは連立方程式を行列に表してみる。
(※この変換がわからない人は下記の行列を展開させてみるとわかる。)
\left(
\begin{array}{ccc}
1 & 1 & 1\\
1 & 2 & 1\\
1 & 1 & 1
\end{array}
\right)
\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)
=
\left(
\begin{array}{c}
1\\
2\\
2
\end{array}
\right)
\\
⇔
\\
Ax=b
さて、ランクを計算するには、$A$に対して階段行列というちょっと変わった行列操作を行う。
この行列操作を代わりに行ってくれるライブラリはいくらでもあるので。ここでは割愛する。
[A]を階段行列とすると、以下のようになる。
[A]=
\left(
\begin{array}{ccc}
1 & 1 & 1\\
0 & 1 & 0\\
0 & 0 & 0
\end{array}
\right)
階段行列とは文字通り階段。左下のほうに0が連なっているのがわかる。
[A]では3行目が全て0なので、段数は2つ。この段数をrankとよび、$rankA=2$が求まる。
このようにして求められたランクと、行列と未知数の数の関係で
その連立方程式の解がどのようになるかが予測できる。
(1)Aがフルランク行列のとき ⇔ rankA = min((Aの横の長さ) , (Aの縦の長さ))のとき
1.rankA=(Aの横の長さ)=(Aの縦の長さ) ⇔ Aが正方形の行列
理想的。方程式(データ)の数も十分なうえに、各方程式に矛盾も重複もない。
正則行列なので逆行列が存在し、$x=A^{-1}b$より一意の解が求められる。
\left\{
\begin{array}{ll}
x+y=2\\
x-y=2
\end{array}
\right.
⇔
\left(
\begin{array}{c}
1 & 1\\
1 & -1
\end{array}
\right)⇔
rankA=2
2.rankA=(Aの横の長さ)<(Aの縦の長さ) ⇔ Aが縦長の行列
方程式(データ)の数はたくさんあるが、方程式の変数が足りていない。
満たさなければいけない方程式が多すぎてすべての条件を満たせない状態、
よって解が存在しない。不能の状態。
\left\{
\begin{array}{ll}
x+y=2\\
x-y=2\\
x-2y=2
\end{array}
\right.
⇔
\left(
\begin{array}{c}
1 & 1\\
1 & -1\\
1 & -2
\end{array}
\right)⇔
rankA=2
3.rankA=(Aの横の長さ)>(Aの縦の長さ) ⇔ Aが横長の行列
方程式には未知数を表せるだけの変数が存在するが、方程式の数が足りない。
条件が緩すぎて、解が無限に存在する。不定の状態。
\left\{
\begin{array}{ll}
x+y+z=2\\
x-y+2z=1\\
\end{array}
\right.
⇔
\left(
\begin{array}{c}
1 & 1 & 1\\
1 & -1 & 2\\
\end{array}
\right)⇔
rankA=2
(2)Aがフルランク行列でないとき ⇔ rankA < min((Aの横の長さ) , (Aの縦の長さ))のとき
4.解が存在しない
ランク落ちとよぶ。
このルールにより、連立方程式の解がどうなるか調べられる。
それでは実際に適当な行列で解を求めて、ルールに一致しているか確認してみる。
(解の求め方は省略)
\left\{
\begin{array}{ll}
x + 2z = 0\\
y " 3z = 0\\
\end{array}
\right.
\\
⇔\\
Ax=
\left(
\begin{array}{c}
1 & 0 & 2\\
0 & 1 & -3 \\
\end{array}
\right)
\left(
\begin{array}{c}
x \\
y \\
x
\end{array}
\right)\\
⇔
\\
\\
\left(
\begin{array}{c}
x \\
y \\
z
\end{array}
\right)
=
a
\left(
\begin{array}{c}
-2 \\
3 \\
1 \\
\end{array}
\right)
以上のように、$Ax=0$の解$x$は1つの列ベクトルとパラメータ$a$で表現された。
パラメータ$a$にはどんな値を入れても連立方程式が成立することを表しており、
$Ax=0$の解は解が無限に持つことが表現している。
次に、先ほどのルールに当てはめて検証してみる。
解が無限なので有れば、3のパターンになりそう。どうなるだろうか。
AのランクはrankA=2。横縦の長さの最小値は2なので一致するため、
Aはフルランクの行列。よって(1)のパターン。
そして、横長の行列であるので、3のパターン。よってルールに合致することが確認できた。
以上が、解の状態を確認するルールとなる。
ちなみに、$(-2,3,1)$のように$(x,y,z)$を表す列ベクトルのことを基底と呼ぶ。
また余談だが、(未知数の数-rankA)より、解が無限になるときのパラメータの数を
事前に調べることが可能である。(未知数の数-rankA)を自由度と呼ぶ。
さきほどの例だと、3-rankA=3-2=1よりパラメータは1個になり、$a$だけで解を表すことができた。
・・・
・・
・
・・・・それにしても解が無限というのはもやっとする回答である。
実際にこの解で何かしようとしたとき、
「解が無限なので求まりません!」だとあまりに都合がわるい。
https://www.slideshare.net/wosugi/ss-79624897
上記サイトによれば、このような場合はラグランジュの未定乗数法でとけるらしい。
上記サイトでは方程式の解の様々なパターンに対するアプローチが
めちゃくちゃ整理されて書かれてある。興味のある人はどうぞ
【参考】
https://gijyutsu-keisan.com/science/numcal/matrix/simultaneous/simultaneous_1.php
http://www2.kaiyodai.ac.jp/~yoshi-s/Lectures/LAlgebra/2015/LinearSystems2.pdf
(4-2)基礎行列Fの等式から解のパターンを分類する
ということで、ランクの考え方を$F$に使用して、どのような解になるかを予想する。
\left(
\begin{array}{c}
a_{1}u_{1} & a_{1}v_{1} & a_{1} & b_{1}u_{1} & b_{1}v_{1} & b_{1} & u_{1} & v_{1} & 1 \\
a_{2}u_{2} & a_{2}v_{2} & a_{2} & b_{2}u_{2} & b_{2}v_{2} & b_{2} & u_{2} & v_{2} & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
a_{n}u_{n} & a_{n}v_{n} & a_{n} & b_{n}u_{n} & b_{n}v_{n} & b_{n} & u_{n} & v_{n} & 1
\end{array}
\right)
\left(
\begin{array}{ccccccccc}
F_{11}\\
F_{12}\\
F_{13}\\
F_{21}\\
F_{22}\\
F_{23}\\
F_{31}\\
F_{32}\\
F_{33}
\end{array}
\right)
=0\\
⇔\\
Af=0
先ほどのこの式。
まずはrankAの値はいくつになるか考えてみる。
かんがえ・・・る・・・・・。
かんがえたけど・・・・。
・・・・・
・・・・
・・・
・・
・
↓↓説明できませんでした↓↓↓
ランクがいくつになるかはわかったけど、なぜそうなるかはわかりませんでした・・。
以降、調べたことをそのまま書くけど、曖昧なので読まなくてもよい。
様々なサイトを見た話をそのまま書くと、
$f$のランクは2なので自由度は(変数の個数)-rankf=9-2=7。
ちなみに$f$のランクが2の理由は、
$F$はスケール不定であることと、同次座標であることが理由、らしい。
自由度7なので、必要な方程式の数は最低7つ。
よって特徴点の組が7つが最低限必要となる、らしい。
あれ?というかなんで私はrankAじゃなくrankfを求めてるんだ?
・・・まぁ、この値はそもそも、方程式をとけるかどうか、必要な式はいくつかを
調べるためにやってることだし、答えはわかったからもういいや・・・。
【参考】
https://www.quora.com/Why-is-the-fundamental-matrix-in-computer-vision-rank-2
https://stackoverflow.com/questions/49763903/why-does-fundamental-matrix-have-7-degrees-of-freedom
http://web.wakayama-u.ac.jp/~wuhy/CV11.pdf
↓↓続きます↓↓↓
・・・・
・・・
・・
・
(4-3)基礎行列の算出アルゴリズムをいくつか紹介
とにもかくにもランクは7。ランク落ちに分類されるパターンである。
ランク落ち・・・解が存在しないパターンである。(どうやって解くんだ・・・?)
$F$を求めるアルゴリズムとしていくつかあるが、ここでは2つを説明する。
(1)8つの特徴点の組を使用する7点アルゴリズム 8 point algorithm
(2)7つの特徴点の組を使用する8点アルゴリズム 7 point algorithm
点群作成用の有名所のオープンソースを見ると、OpenMVGやColmapではデフォルトで7点アルゴリズムを採用していた。
7点アルゴリズムのほうが性能的にはいいのかな?
が、ここではのちの説明のために都合の良い8点アルゴリズムのほうを説明する。
【参考】
http://www.iedu.i.kyoto-u.ac.jp/uploads/20141022.pdf
http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/MOHR_TRIGGS/node50.html
https://github.com/Kanwarme/EpipolarGeometry_FundamentalMatrix/blob/master/fundamentalMatrix.py
http://dhoiem.cs.illinois.edu/courses/vision_spring10/lectures/Lecture22%20-%20Epipolar%20Geometry.pdf
http://www2.kaiyodai.ac.jp/~yoshi-s/Lectures/LAlgebra/2015/LinearSystems2.pdf
(4-4)基礎行列Fの推定 ~ 8点アルゴリズム
8点アルゴリズム(Eight-point algorithm)ではまず8個の特徴点の組を用意する。
すると、$F$の式は以下のようになる。
\left(
\begin{array}{c}
a_{1}u_{1} & a_{1}v_{1} & a_{1} & b_{1}u_{1} & b_{1}v_{1} & b_{1} & u_{1} & v_{1} & 1 \\
a_{2}u_{2} & a_{2}v_{2} & a_{2} & b_{2}u_{2} & b_{2}v_{2} & b_{2} & u_{2} & v_{2} & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
a_{8}u_{8} & a_{8}v_{8} & a_{8} & b_{8}u_{8} & b_{8}v_{8} & b_{8} & u_{8} & v_{8} & 1
\end{array}
\right)
\left(
\begin{array}{ccccccccc}
F_{11}\\
F_{12}\\
F_{13}\\
F_{21}\\
F_{22}\\
F_{23}\\
F_{31}\\
F_{32}\\
F_{33}
\end{array}
\right)
=0\\
⇔\\
Af=0
この式を$Af=0$とする。
$Af=0$を中学生の時に教わった知識で解くこともできなくはないが、
もしも選択された8つの特徴点の組に誤りがあった場合、あるいは
無関係なノイズの組が存在した場合、仮に解が求まったとしても
解が誤ってるケースがかなり高いだろう。
画像のような実データを扱った連立方程式は、
中学生のころの連立方程式とは違ってノイズの影響も考えなければならない。
8点アルゴリズムでは、ノイズに対してある程度頑強な手法により$F$を求める。
以下にその流れを記載する。
8点アルゴリズム - 同次形方程式の最小二乗問題
本題に行く前に改めてこの疑問を問わなければならない。
「この方程式で正しい答えが導けるの?」という問題。
繰り返すが、特徴点マッチングがうまく行かずに方程式そのものがダメな場合も考えられる。
というかたぶんだめである。ランク落ちしているので解は求まらない。
ということで
「どうせ$Af=0$をきれいに満たす解なんてないんだから、
$Af≒0$みたいな限りなく0に近づける解$f$を探そうぜ」
というスタンスのもと、$Af$を0に近づける$f$、
すなわち$Af$が最小値となる$f$を求めることに注力する。
とりあえずは、ベクトルで比較すると正負の向きの影響を受けるので、
単純な大きさを比較するために絶対値の時の最小値を求めることを方針に掲げてみる。
|Af|=min
右辺のminというのは、最小値を求めますよーというのを表している。
これがいわゆる「最小絶対値法」である。
これに対して、より一般的でポピュラーなのが「最小二乗法」。
|Af|^{2}=min
一般的には「最小二乗法」のほうが評価が高いけど、
場合によっては「最小絶対値法」のほうがいいこともあるらしい・・・?
そのうち調査してみたいところではあるけど、ここでは一旦やらないでおく。
このページでは、一般的な$F$の推定に用いられる「最小二乗法」のほうを採用して以下に記載する。
|Af|^{2}=min
とにもかくにも、
掲げる目標としては、$|Af|^{2}$を最小値にする$f$を求める事。
このスタンスに則ったとき、めちゃくちゃ役立つのが
特異値分解、Singular Value Decomposition (SVD)というものである。
以下にSVDについて詳しく見てみる。
基本知識7 特異値分解 Singular Value Decomposition (SVD)
再び脱線基本知識のコーナー。
基本知識の難易度が徐々に大学数学に到達してきた。
特異値分解は行列を「都合のいい」行列に分解して表現してみようという行列変換方法である。
式は下記のとおりである。
$A=UΣV^{T}$
イメージを掴むために実際の特異値分解の結果を先に提示する。
A=\left(
\begin{array}{cc}
1 & 3 \\
2 & 2 \\
3 & 1
\end{array}
\right)
\\
⇔
\\
A=UΣV^{T}=
\left(
\begin{array}{cc}
\frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{3}} & 0 \\
\frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{2}}\\
\end{array}
\right)
\left(
\begin{array}{cc}
2\sqrt{6} & 0\\
0 & 2
\end{array}
\right)
\left(
\begin{array}{cc}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{array}
\right)
\\
このSVDの便利なところはどんな行列でも適用できる点である。
「どんな行列でも」というのがポイントである。以前、逆行列について説明した。
逆行列もめちゃクソ便利で、$Ax=b$とあれば$x=bA^{-1}$として、Aについて逆行列で解くことができる。
しかし、逆行列は実はすべての行列に必ずしも存在するものではない。
$A$の縦横の長さが同じでなければならない等の条件があるのだ。
その点、SVDはどんな行列にも対応可能である。
詳しく知りたい人は疑似逆行列で調べてください。(今回はそこには触れない)
以降、SVDの活用方法や性質はいくつかあるが、
このページにおいて特に関わりの深いものについて以降に記載する。
★正規直交基底U,Vのノルム
$\boldsymbol{|U|=1,|V|=1}$
$U,V$は正規化されているので、ノルム(大きさ)は1である。
ちなみに正規化とはベクトルの長さを1に縮尺させること。
★正規直交基底U,Vの転置行列
$\boldsymbol{UU^{T}=I,VV^{T}=I}$
$U,V$は直交行列なので上記式の解は単位行列となる。
そのへんの普通の行列だとこうはならない。不思議。
実際に計算してみると単位行列になるので興味のある人はどうぞ。
★Σは対角行列
\boldsymbol{Σ=
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
& & & \sigma_{ r } \\
0 & & & & 0
\end{pmatrix}
\end{eqnarray}
}
対角線上ににのみ値をもつ行列を対角行列と呼ぶ。
対角線上には特異値と呼ばれる数値が並ぶ。特異値\sigmaは順番は大きい順に並ぶ。
rankAの値分だけ特異値が現れ、それ以降は0が連なる。
★Ax=0とAx=bの解空間がわかる
「行列のランクに関する基本知識」の項にて、
階段行列という特殊な行列操作を行うことでその行列のランクが求まることを触れた。
実はSVDさえ求まっているならそのような操作は必要ない。
「Σは対角行列」の項でも触れたが、
$A$のランクの値分だけ対角線上に特異値が数字となって現れるので、
階段行列を作らずともSVDの$Σ$の対角線上にいくつ数字があるかを見るだけでランクの判別が可能となる。
実際にどんな感じで確認できるかやってみる。
もしも$A$のランクが$rankA=r$であれば、$A$を特異値分解して得られる$Σ$は以下のようになる。
Σ=
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
& & & \sigma_{ r } \\
0 & & & & 0
\end{pmatrix}
\end{eqnarray}
上記のようになるので、特異値の有無を見るだけでランクがわかる。
以上がランクを確認する方法。しかし、この項で説明したいポイントはランクではなく別のところ。
上記の式を見ると、
「特異値を値に持つ箇所」と、
「特異値が0の箇所」
の2つの領域が存在することがわかる。
添字でグループ分けすれば、
「特異値を値に持つ箇所は添字が1~r」
「特異値が0の箇所はr+1~m」
である。
それを念頭に置いて、SVDに分解された各行列を詳しく見てみる。
A=UΣV^{T}=
(u_{1} u_{2} \cdots u_{n})
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
& & & \sigma_{ r } \\
0 & & & & 0
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{c}
v_{1}^{T} &
v_{2}^{T} &
\cdots &
v_{n}^{T}
\end{array}
\right)
行列$V$は、$v_{1}^{T}$~$v_{n}^{T}$の列ベクトルで構成されている。
脱線するが念のため、列ベクトル$(v_{1}^{T}$ $v_{2}^{T}$ $\cdots$ $v_{n}^{T})$という表記について触れると、
V=\left(
\begin{array}{c}
1 & 2 \\
3 & 4
\end{array}
\right)
という行列なら、$v_{1}=(1 , 3)$と$v_{2}=(2 , 4)$となる。
さて本題。
さきほど分類した2つのグループ。
それぞれのグループの添字に該当する列ベクトルには、実はちょっとした意味がある。
(1)特異値が0のグループの列ベクトル ⇔ Ax=0の解がわかる!
「特異値が0の箇所である添字が(r+1)~mのグループ」について。
$V$で言えば、$v_{r+1}$~$v_{m}$にあたるこれらの列ベクトルは
実は$Ax=0$の解$x$を構成する列ベクトルとなるのである。
以下に、実際にどのように解がもとまるかを見てみる。
適当な行列$A$を特異値分解してみる。
A=\left(
\begin{array}{cc}
2 & 0 & 2\\
0 & 1 & 0\\
0 & 0 & 0
\end{array}
\right)
\\
⇔
\\
A=UΣV^{T}=
\left(
\begin{array}{cc}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{cc}
2.8284 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{cc}
0.701 & 0 & -0.701\\
0 & 1 & 0\\
0.701 & 0 & 0.701
\end{array}
\right)
真ん中の$Σ$の行列を見てみる。
特異値が0の位置は3つめなので、先程のルールに則れば
解を構成する列ベクトルは$v_{3}$となるはず。
よって、パラメータを$a$として$Ax=0$のときの解$x$を表すと、下記式となる。
Ax=0
\\
⇔
\\
x=sv_{3}=
a
\left(
\begin{array}{cc}
-0.701\\
0\\
0.701
\end{array}
\right)
これが、$Ax=0$の解となる。$a$にはどんな値も入りうるので
$v_{3}$の無限の定数倍のベクトルが解になる・・・ということらしい。。。
・・・・いやほんまかいな。小数点とか出ちゃってるけど・・・。
ためしに$a=1$として$Ax=0$に入れてみる。正しければ$Ax$は0になるはずだが・・・。
A\left(
\begin{array}{cc}
-0.701\\
0\\
0.701
\end{array}
\right)
=
\left(
\begin{array}{cc}
2 & 0 & 2\\
0 & 1 & 0\\
0 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{cc}
-0.701\\
0\\
0.701
\end{array}
\right)
=
\left(
\begin{array}{cc}
2\cdot-0.701 + 0\cdot0 + 2\cdot0.701\\
0\cdot-0.701 + 1\cdot0 + 0\cdot0.701\\
0\cdot-0.701 + 0\cdot0 + 0\cdot0.701
\end{array}
\right)
=
\left(
\begin{array}{cc}
0\\
0\\
0
\end{array}
\right)
ぜ、ぜろになりましたね・・・!
ということで、$Ax=0$が満たすことが確認できました。
したがって、$Ax=0$の解は、
「$A=UΣV^{T}$と特異値分解SVDしたときの直交行列$V$のうち、
$Σ$の特異値が0になる箇所に該当する$V$の列ベクトルで表すことができる。」
これを別の言い方をすると、零空間を基底でもって表せる、といいます。
(2)特異値に値を持つグループの列ベクトル ⇔ Ax=bの解がわかる!
(1)と似たような感じで、今度は$U$の列ベクトルを用いることで、
$b$の解がわかります。Wikipediaでは値域の基底という呼び方をしていました。
★低ランク近似 Low rank approximation
特異値分解は画像圧縮なんかにも活用できる。以下に詳しく見てみる。
$A=UΣV^{T}$を展開させて整理してみると、以下の式が得られる。
($U$はm×m、$Σ$はm×n、$V$はn×m)
A=
\left(
\begin{array}{c}
a_{11} & \cdots & a_{1n}\\
\vdots & \cdots & \vdots\\
a_{m1} & \cdots & a_{mn}\\
\end{array}
\right)
=(u_{1} u_{2} \cdots u_{n})
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
& & & \sigma_{ r } \\
0 & & & & 0
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{c}
v_{1}^{T} &
v_{2}^{T} &
\cdots &
v_{n}^{T}
\end{array}
\right)
\\
⇔\\
A=\sigma_{1}u_{1}v_{1}^{T} + \sigma_{2}u_{2}v_{2}^{T} +\cdots + \sigma_{r}u_{r}v_{r}^{T}
$A$は$\sigma uvT^{T}$の項がいくつも連なる形で表現される。
\sigmaは以下のような大きさで並ぶ。
\sigma_{ 1 } > \sigma_{2} > \cdots > \sigma_{r}
\sigmaが小さいほど、$A$に与える影響が限りなく小さい特徴がある。
逆に\sigmaが大きいと影響度が大きいので、大きい特異値の項さえあれば十分に行列$A$を表現できる。
言葉で説明するとわかりづらいので、これを画像で示すと以下のようになる。
白黒のデジタル画像は0~255の値を持つ大きな行列である。
白黒画像に対して$A=UΣV^{T}$を取得し、$\sigma uvT^{T}$の項の小さいものを除去すると上記画像のように表される。
Rank5
A_5=\sigma_{1}u_{1}v_{1}^{T} + \sigma_{2}u_{2}v_{2}^{T} + \sigma_{3}u_{3}v_{3}^{T} + \sigma_{4}u_{4}v_{4}^{T} + \sigma_{5}u_{5}v_{5}^{T}
Rank8
A_8=\sigma_{1}u_{1}v_{1}^{T} + \sigma_{2}u_{2}v_{2}^{T} + \sigma_{3}u_{3}v_{3}^{T} + \sigma_{4}u_{4}v_{4}^{T} + \sigma_{5}u_{5}v_{5}^{T} + \cdots + \sigma_{8}u_{8}v_{8}^{T}
Rankは$\sigma uvT^{T}$の項の数を示しており、上記式のように上から$\sigma uvT^{T}$の項を残していく。
画像を見ると、画像の行列$A$は概ね以下のRankで近似される。
A=A_{47}≒A_{46}≒ \cdots ≒A_{23}
このように、\sigmaの添字が後ろのほうのものを除外して近似させることを低ランク近似と呼ぶ。
SVDでは、影響度の大きいものと小さいものを分解してこのように近似させることが可能となる。
★行列に対するランクの調整
特異値分解を用いるとノイズの影響でランクが大きくなってしまったデータのランクを
小さくすることでノイズの影響を抑えることが可能である。
ということで、とある$Ax=0$を求めようとしたケースを例に考えてみる。
前提としては、$x$の未知数は9個、ランクは2とする。
このときの自由度は9-2=7になるため、$x$は7つの未知数の列ベクトルの組で
解$x$は表現されることが予想される。
このような前提がある中で、実際のデータを用いて$Ax=0$の式を作成し、
なんとかかんとか$Ax=0$の解$x''$を求めた。
しかし、実際のデータを扱っている想定なので、
実データのノイズにより$x''$は必ず理想的な値とは少なからず異なる値を出力していた、とする。
具体的には、$x''$は本当はランクが2になるはずが、
$x''$のランクを計算してみるとランクが9になっていた、というケースを考える。
ノイズの存在が、ランク2になるはずの行列をランク9まで増やしてしまっている状態である。
なんとかしてランクを増やす要因を除きたい。
このようなときに有効なのが特異値分解である。
まずは求められた$x''$を特異値分解で分解してみる。
x''=UΣV^{T}=
(u_{1} u_{2} \cdots u_{9})
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
& & & \sigma_{ 9 }
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{c}
v_{1}^{T} &
v_{2}^{T} &
\cdots &
v_{9}^{T}
\end{array}
\right)
「Σは対角行列」の項において、$Σ$に現れる特異値の数がそのままランクになることを触れた。
したがって、$x''$はノイズによりランクが9に上がっているため、
$x''$の特異値分解には$\sigma_{3}$~$\sigma_{9}$が現れる。
非常に小さいノイズが、$\sigma_{3}$~$\sigma_{9}$にあらわれてしまった結果、上式のような結果となっている。
$\sigma_{3}$~$\sigma_{9}$の項にはノイズが集中する。
理想的な$x$はランク2なので必要な特異値は、$\sigma_{1}$と$\sigma_{2}$の情報である。
よって、ノイズが集中している$\sigma_{3}$~$\sigma_{9}$を除外してしまえば良い。
低ランク近似の項で説明したとおり、添字が小さいものは影響度が小さいため、
$\sigma_{3}$~$\sigma_{9}$を除外しても近似することが可能となる。
したがって、微小なノイズを除外した$x_{filter}$は以下のようになる。
x_{filter}
=
UΣV^{T}=
(u_{1} u_{2} \cdots u_{9})
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & \\
& \sigma_{ 2 } & & \\
& & 0 & \\
& & & 0
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{c}
v_{1}^{T} &
v_{2}^{T} &
\cdots &
v_{9}^{T}
\end{array}
\right)
特異値は2つしかないのでランクは2。
これにより、$x''$からノイズを除去することができた。
8点アルゴリズム - 特異値分解による総最小二乗法 SVD for Total Least Squares
ようやく準備は整った。さっそく$Af=0$を解いてみる。
その前に、今のままだと条件がゆるすぎるので制約条件なるものを考える。
$Af=0$において、f=0は確実に解になるが、
f=0は明らかに不要なので下記の制約条件を与える。
|f|=1
||でベクトルを挟む表記をノルムと呼ぶ。ノルムはベクトルの長さを表す記号。
式の意味としては、fの長さは絶対1だから0じゃないよーということを言っている。
この条件がめちゃくちゃ重要なので、この式を念頭に置いてほしい。
加えて、どこかの項でfのランクはrankf=2であることについて触れた。
この条件も最終的に使用することとなるので、覚えておきたい。
・・・
・・
・
まずは方針の確認。
上の方に書いたとおり、$min||Af||^{2}$をベースに考える。
$||Af||^{2}$の最小値にする$f$を求めようぜ、という方針である。
それではさっそく最小値を求めてみよう。
SVDの基本知識の項で説明した$A=UΣV^{T}$を代入してみる。
min||UΣV^{T}f||^{2}
次に、$U$の項を分けてみる。($|AB|=|A||B|$)
min||U|| ||ΣV^{T}f||^{2}
SVDの基本知識の項にて、$U$は正規直交行列なのでノルムが1であることを述べた。($|U|=1$)
このことから下記の式を得る。
min||ΣV^{T}f||^{2}
次に、$y=V^{T}f$として未知数$f$を$y$に置き換える
min||Σy||^{2}
これにより、最小値化する$f$を求める問題が、最小値化する$y$を求める問題に置き換わる。
min||Σy||^{2}
ということで、$Σy$の中身を整理してみる。
まずは$Σ$の中身について。SVDの基本知識で述べたとおり、
対角行列$Σ$は下記のようにあらわされる。
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
0 & & & \sigma_{ 9 }
\end{pmatrix}
\end{eqnarray}
なお、特異値\sigmaは下記の大小関係が存在する。
\sigma_{1}>\sigma_{2}> \cdots >\sigma_{9}
そして$Σ$をもとに$Σy$を式にすると下記のようになる。
Σy=
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
0 & & & \sigma_{ 9 }
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{ccccccccc}
y_{1}\\
y_{2}\\
y_{3}\\
y_{4}\\
y_{5}\\
y_{6}\\
y_{7}\\
y_{8}\\
y_{9}
\end{array}
\right)
=
\left(
\begin{array}{ccccccccc}
y_{1}\sigma_{ 1 }\\
y_{2}\sigma_{ 2 }\\
y_{3}\sigma_{ 3 }\\
y_{4}\sigma_{ 4 }\\
y_{5}\sigma_{ 5 }\\
y_{6}\sigma_{ 6 }\\
y_{7}\sigma_{ 7 }\\
y_{8}\sigma_{ 8 }\\
y_{9}\sigma_{ 9 }
\end{array}
\right)
そして$Σy$をノルムにしてベクトルの大きさ$|Σy|$を求めると下記のようになる。
|Σy|=
\sqrt{
(y_{1}\sigma_{ 1 })^{2}+
(y_{2}\sigma_{ 2 })^{2}+
(y_{3}\sigma_{ 3 })^{2}+
(y_{4}\sigma_{ 4 })^{2}+
(y_{5}\sigma_{ 5 })^{2}+
(y_{6}\sigma_{ 6 })^{2}+
(y_{7}\sigma_{ 7 })^{2}+
(y_{8}\sigma_{ 8 })^{2}+
(y_{9}\sigma_{ 9 })^{2}+
}
したがって、上式を$||Σy||^{2}$に当てはめると、
最小化問題は下記のようにさらに置き換わる。
min||Σy||^{2}
\\
⇔
\\
min
((y_{1}\sigma_{ 1 })^{2}+
(y_{2}\sigma_{ 2 })^{2}+
(y_{3}\sigma_{ 3 })^{2}+
(y_{4}\sigma_{ 4 })^{2}+
(y_{5}\sigma_{ 5 })^{2}+
(y_{6}\sigma_{ 6 })^{2}+
(y_{7}\sigma_{ 7 })^{2}+
(y_{8}\sigma_{ 8 })^{2}+
(y_{9}\sigma_{ 9 })^{2})
最小化問題は上記式が最小となる$y_{1}$~$y_{9}$を求めることにより帰着する。
$y_{1}$~$y_{9}$はどうすれば求まるだろう?
ここで最初に提示した制約式を振り返る。
冒頭、$Af=0$の解$f$が0でないことを示すために$|f|=1$の制約を設けた。
この式をちょっと変えてみる。SVDの基本知識より、$V^{T}$は$|V^{T}|=1$になる。
このことから、$|f|=1$は下記のように書き換えられる。
|y|=|V^{T}x|=|V^{T}||x|=1
したがって、$|y|=1$の制約式を見出した。
次に、$|y|=1$を満たす$y_{1}$~$y_{9}$を考えたとき、
$y_{1}$~$y_{9}$のうち、1つだけ1で、ほかがすべて0であれば必ず$|y|=1$を満たすはずである。
y=(0,0,0,\cdots,1,\cdots,0)
\\
⇔
\\
|y|=
\sqrt{
0^{2}+
0^{2}+
\cdot
+1^{2}+
}=1
じゃあ、どれが1になるの?という話だが、
SVDの基本知識では、$\sigma$の添え字が大きいものほど値が小さくなることを述べた。
今求めたいのは$|Σy|$の最小値なので、一番小さい$\sigma$だけがある状態が最も最小値である。
最小の$\sigma$は$\sigma_{ 9 }$
よって、$y_{ 9 }=1$でいて、かつ他すべての値が0であれば、
$\sigma_{ 9 }$だけが残り、最小値が得られるはず。
以上の事から下記式が求まる。
|Σy|=
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
0 & & & \sigma_{ 9 }
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{ccccccccc}
0\\
0\\
0\\
0\\
0\\
0\\
0\\
0\\
1
\end{array}
\right)
=
\sigma_{ 9 }
求めたいのは$f$である。式は$y=V^{T}f$のように示したので、
これをfについて解いてみる。左から$V$をかけてみる。
y=V^{T}f
\\
⇔
\\
Vy=VV^{T}f
\\
SVDの基本知識より、$VV^{T}=I$とおけるので(これができるのがSVDの強いところ!)
以下の式になる。
Vy=VV^{T}f
⇔
\\
Vy=f
\\
⇔
\\
f=Vy
以上より、$f$は$f=Vy$に書き換えられる。
$V$は列ベクトルの集合なので、
$V=(v_{1} v_{2} \cdots v_{9})$とすれば、
$y$により9番目の$V$の列ベクトルが抽出され以下の式となる。
f=v_{9}
$v_{9}$は$A$をSVDした時点ですでに取得できており既知である。
これにより、基礎行列$f$は求まった!!!
・・・・
・・・
・・
・
とはならないのが悲しいところ・・・。
最後のちょっとした操作がどうしても必要になる。
8点アルゴリズムはここで終わらない。
それらしい$F$は見つかったが、それでもノイズの影響を受けてるかもしれない。
と、いうことでSVDによりランクの調整を行う。
やることは、SVDの基本知識のランクの調整に記載したとおりである。
小さなノイズの影響を受けると、小さな特異値が生まれてランクが大きくなるので、
SVDで行列を分解することで、小さな特異値を覗いてしまおうという話。
fのランクは2になるはず、ならなければならないので
ランクが大きくなっているときはランクを2にしてノイズの除去を行う。
これにてfは求まった。
以下に、すごく簡単にmatlabによる8点アルゴリズムを説明する。
下記ソースコードをざっくりと説明して、記載する。
https://github.com/MareArts/8point-algorithm/blob/master/GetFmatrix_Final.m
A=[x1(:,1).*x2(:,1) x1(:,2).*x2(:,1) x2(:,1) x1(:,1).*x2(:,2) x1(:,2).*x2(:,2) x2(:,2) x1(:,1) x1(:,2), ones(s,1)];
特徴点の組を入れて下記を計算している。
A=\left(
\begin{array}{c}
a_{1}u_{1} & a_{1}v_{1} & a_{1} & b_{1}u_{1} & b_{1}v_{1} & b_{1} & u_{1} & v_{1} & 1 \\
a_{2}u_{2} & a_{2}v_{2} & a_{2} & b_{2}u_{2} & b_{2}v_{2} & b_{2} & u_{2} & v_{2} & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
a_{8}u_{8} & a_{8}v_{8} & a_{8} & b_{8}u_{8} & b_{8}v_{8} & b_{8} & u_{8} & v_{8} & 1
\end{array}
\right)
[U D V] = svd(A);
F=reshape(V(:,9), 3, 3)';
$A$のSVDを計算したあとに、$v_{9}$を取得。
もはやはるか昔の話だが、$F$は下記の式のもとで9×1のベクトルに置き換わっているので、
9×1の列ベクトル$v_{9}$を下記の対応関係に矛盾がないように3×3に配置する。
\left(
\begin{array}{c}
u & v & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
F_{11} & F_{12} & F_{13} \\
F_{21} & F_{22} & F_{23} \\
F_{31} & F_{32} & F_{33}
\end{array}
\right)
\left(
\begin{array}{ccc}
a \\
b \\
1
\end{array}
\right)
=
0
A=\left(
\begin{array}{c}
a_{1}u_{1} & a_{1}v_{1} & a_{1} & b_{1}u_{1} & b_{1}v_{1} & b_{1} & u_{1} & v_{1} & 1 \\
a_{2}u_{2} & a_{2}v_{2} & a_{2} & b_{2}u_{2} & b_{2}v_{2} & b_{2} & u_{2} & v_{2} & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
… & … & … & … & … & … & … & … & 1 \\
a_{8}u_{8} & a_{8}v_{8} & a_{8} & b_{8}u_{8} & b_{8}v_{8} & b_{8} & u_{8} & v_{8} & 1
\end{array}
\right)
\left(
\begin{array}{ccccccccc}
F_{11}\\
F_{12}\\
F_{13}\\
F_{21}\\
F_{22}\\
F_{23}\\
F_{31}\\
F_{32}\\
F_{33}
\end{array}
\right)
=0\\
% make rank 2
[U D V] = svd(F);
F=U*diag([D(1,1) D(2,2) 0])*V';
$f$のランクは必ず2になり、$D$に$D(3,3)$$D(4,4)$とあってもそれらは必ずノイズになるはずである。
なので、上記で述べたとおりSVDによりランクの調整を行う。
これによりFが求まる。
以上が8点アルゴリズムの概要である。
【参考】
https://thinkit.co.jp/article/16884
https://www2.math.ethz.ch/education/bachelor/lectures/hs2014/other/linalg_INFK/svdneu.pdf - Theorem2.3
http://www.cs.cmu.edu/~16385/s17/Slides/11.5_SVD.pdf
http://www.iedu.i.kyoto-u.ac.jp/uploads/20141022.pdf
https://foto.aalto.fi/seura/julkaisut/pjf/pjf_e/2005/Inkila_2005_PJF.pdf
http://cmp.felk.cvut.cz/cmp/courses/XE33PVR/WS20072008/Lectures/Supporting/constrained_lsq.pdf
http://sssiii.seesaa.net/article/383104769.html
https://github.com/MareArts/8point-algorithm/blob/master/GetFmatrix_Final.m
http://www.cs.cmu.edu/~16385/s17/Slides/12.4_8Point_Algorithm.pdf
https://www2.cs.duke.edu/courses/spring19/compsci527/notes/longuet-higgins.pdf
http://cseweb.ucsd.edu/classes/sp19/cse152-a/hw2/HW2.pdf
(5)基本行列(essential matrix)からカメラ姿勢(回転行列・並進行列)の抽出
(5-1)基礎行列Fから基本行列Eを求める
ということで、画像のピクセル情報から$F$を求めることができた。
①「基礎行$E$がわかれば、三次元座標がわかる!」
↓
②「$F$がわかれば、$E$がわかる!」←いまここ
↓
③「$X$と$X_{R}$がわかれば、$F$がわかる!」←ok
↓
④「画像のピクセルの座標がわかれば、$X$と$X_{R}$がわかる!」←ok
ということで、次はこの$F$を使って$E$を求める。
$F$は$F=K^{-t}E K^{-1}$で表されるので、
E=K^{T}FK
で表される。
Fは8点アルゴリズム等で計算可能なので既知。
Kは焦点距離$f$と画像の主点$Cx,Cy$で構成されているので
画像の解像度とExif情報or機種名がわかれば既知である。
K=\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
Exif情報のないインターネットの画像を使って復元する場合など、
内部パラメータが未知ケースも存在するが、このページでは
カメラ情報が既知である画像を使用することを前提として話をすすめる。
右辺はすべて既知の情報なので単純な行列計算で$E$を求めることができた。
(5-2)射影行列の導出(projection matrix)
はじめに
①「基礎行$E$がわかれば、三次元座標がわかる!」←いまここ
↓
②「$F$がわかれば、$E$がわかる!」←←ok
↓
③「$X$と$X_{R}$がわかれば、$F$がわかる!」←ok
↓
④「画像のピクセルの座標がわかれば、$X$と$X_{R}$がわかる!」←ok
ながい道のりもようやくおわる・・・。
本題の前に、ここまで出てきたカメラに関する変換式を復習してみる。
\left(
\begin{array}{ccc}
u\\
v\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)\\
まずは内部パラメータのときにでたこの式。
この式は、画像上のピクセル座標$(u,v)$を三次元座標$(X,Y,X)$に変換する式である。
今更ながらに振り返るが、ここまでの長い説明は
全ては画像のピクセルを三次元座標に変換する方法を模索するためである。
「この式で三次元座標に変換できるなら、この式だけで十分じゃね?」と思いそうになるが、ちょっと違う。
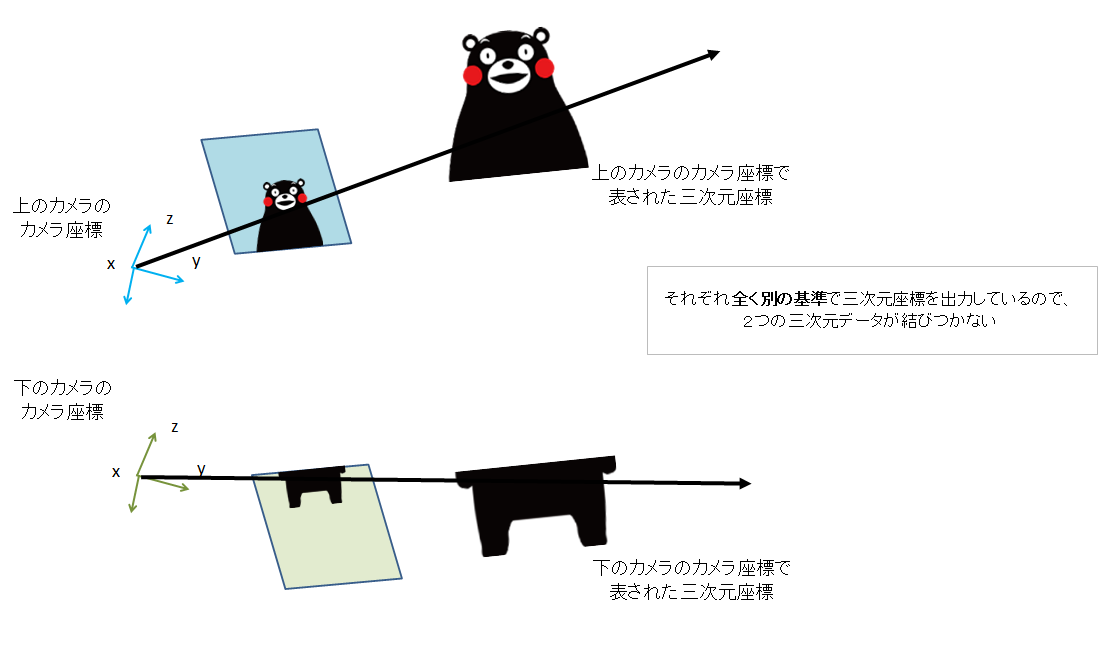
この式で表される三次元座標は「カメラ座標」で出力された三次元座標である。
カメラ単体であればそれで問題ないが、複数のカメラが存在する場合は
基準となる座標がバラバラなので、それぞれの写真から出力された三次元座標が結びつかない。
上記画像のように、別々の写真に写ったクマモンが結びつかなくなるケースが起こる。
したがって、複数枚の写真を結びつけるためには共通の座標が必要となる。
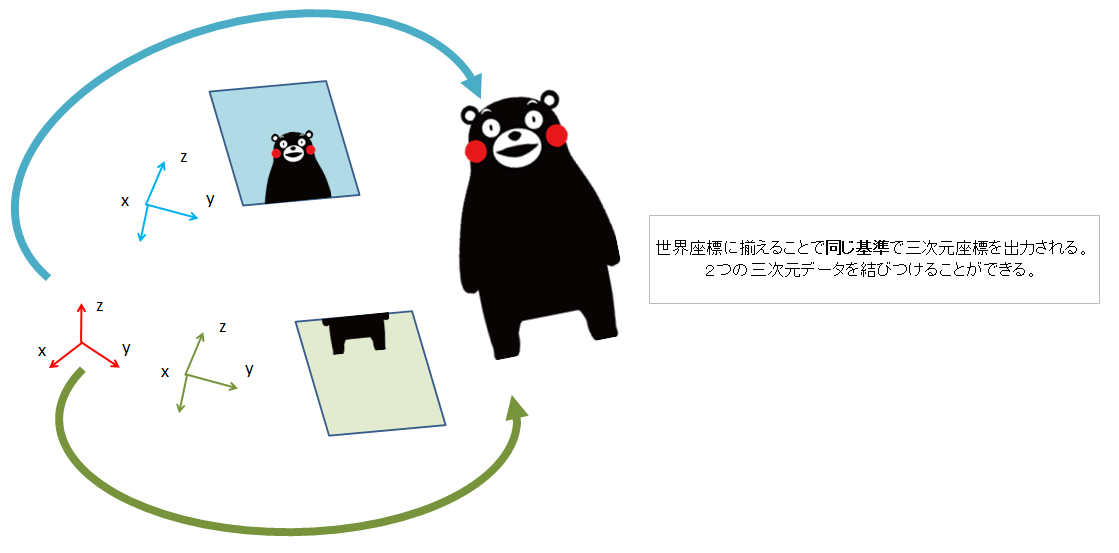
ちなみにこの共通の座標を世界座標と呼ぶ。
カメラ座標で表された三次元座標を世界座標に置き換える必要がある。
イメージ的には上記のようなイメージである。
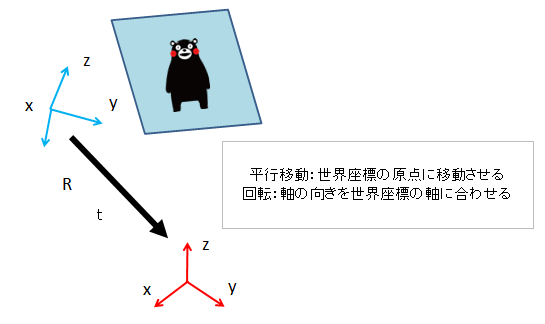
水色がカメラ座標。赤が世界座標。そして、ここで行いたいのは座標軸の変換である。
画像の通り、水色の軸と赤い軸は向きが揃ってないので「回転行列」で回転させてやる必要がある。
さらに距離も離れているので「移動行列」で行列を移動させる必要もあるだろう。
\left(
\begin{array}{ccc}
u\\
v\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
f & 0 & C_{x}\\
0 & f & C_{y}\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
X\\
Y\\
Z
\end{array}
\right)\\
⇔\\
X_{image} = KX_{camera}
ということで、当面の目標としては、カメラ座標で表された上式を世界座標であらわすこと。
最終的には、上記式の$X_{camera}$に世界座標の$X_{world}$を入れて、
「画像上のピクセル座標からカメラ座標を求める式」を
「画像上のピクセル座標から世界座標を求める式」に変換する。
(5-3)カメラ座標から世界座標への変換
さっそくさきほどの画像のように$X_{camera}$を$X_{world}$に移動させる。
回転行列と移動行列をそれぞれ$R$と$T$とすると以下のようになる。
X_{camera} = RX_{world}+T
基礎行列$E$にて回転行列と移動行列を使ったが、まんま同じ計算である。
回転行列$R$は基礎行列$E$でつかった回転行列と同じく3軸で回転するとして、
今までの知識でこの中身を数式で示すなら。
R=
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13}\\
r_{21} & r_{22}& r_{23}\\
r_{31} & r_{32}& r_{33}
\end{array}
\right)
,
T=
\left(
\begin{array}{ccc}
tx\\
ty\\
tz
\end{array}
\right)
\\
X_{camera} = RX_{world}+T\\
⇔
\\
X_{camera} =
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13}\\
r_{21} & r_{22}& r_{23}\\
r_{31} & r_{32}& r_{33}
\end{array}
\right)
\left(
\begin{array}{c}
X\\
Y\\
Z
\end{array}
\right)
+
\left(
\begin{array}{ccc}
tx\\
ty\\
tz
\end{array}
\right)
移動行列の項だけ足し算の形で飛び抜けた形で表現される。
実はこれが地味に厄介なのだ。行列の便利な性質の多くは積で表されているため、
足し算の形で行列が飛び抜けていると、それらの性質が利用できないので非常に不便なのだ。
できることなら、この飛び抜けた式を消してしまいたい。
なんとかして移動行列$T$を$R$の中に組み込んで、$A=BX+t$から$A=B'X$と表現したい・・・。
どうすれば組み込めるだろうか?実は内部パラメータの項にて既ににたようなことをやっている。
「同次座標」という概念を用いることでこれが可能となる。
基本知識8 同次座標
改めて目的を明示的に示すと、
$A=BX+t$のように$t$が飛び出していると、
積で表されている行列の性質の多くが利用できなくなるので、
$A=B'X$という形式になんとか変換させたい。
説明のために、あえて誤った例を提示する。
例えば以下のように考えなしに移動行列$T$を組み込んだとする。
\\
X_{camera} =
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13} & tx\\
r_{21} & r_{22}& r_{23} & ty\\
r_{31} & r_{32}& r_{33} & tz
\end{array}
\right)
\left(
\begin{array}{c}
X\\
Y\\
Z
\end{array}
\right)
これは明らかに誤りである。そもそも、行列の縦横の問題で計算自体ができない。
3×4の行列に対して、3×1の列ベクトルを掛け合わせることは不可能。
ならば単純に、4×1の列ベクトルを増やしたらどうなるだろう?
\\
X_{camera}
=
\left(
\begin{array}{ccc}
X_{camera}\\
Y_{camera}\\
Z_{camera}\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13} & tx\\
r_{21} & r_{22}& r_{23} & ty\\
r_{31} & r_{32}& r_{33} & tz\\
0 & 0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{c}
X\\
Y\\
Z\\
1
\end{array}
\right)
\\
⇔
\\
X_{camera}
=
\left(
\begin{array}{ccc}
X_{camera}\\
Y_{camera}\\
Z_{camera}
\end{array}
\right)
=
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13}\\
r_{21} & r_{22}& r_{23}\\
r_{31} & r_{32}& r_{33}\\
\end{array}
\right)
\left(
\begin{array}{c}
X\\
Y\\
Z
\end{array}
\right)
+
\left(
\begin{array}{ccc}
tx\\
ty\\
tz
\end{array}
\right)
さりげなく下の方に(0 0 0 1)の行ベクトルが追加されているが、
展開すると1=1というごく当たり前の式でしかないことがわかる。
両者を展開して連立方程式にしてみると、全く同じ内容であることがわかる。
このように、行列に対して何も影響を与えない次元を増やしたこのような表記を「同次座標系」と呼ぶ。
上記の式を見てわかるように、移動行列$T$が一つの行列に収まっていることがわかる。
これで行列の性質も利用できる。
ちなみに同次座標という言葉は、内部パラメータの項でも言葉だけ出てきた概念である。
内部パラメータの項では、zの次元を増やすためだけにz=zの式を行列に組み込んだ。
この項では1=1という式を組み込んでいる。
※備考 同次座標のスケール不変性について
後の説明のために、同時座標のとある座標$x$はその定数倍と同じ座標になる性質について触れる。
x=sx
いつもおなじみのXY軸の二次元座標$P=(x_{Euc},y_{Euc})$に、
次元$Z$を追加して同次座標$P'=(X_{Hom},Y_{Hom},Z_{Hom})$を導入したとする。
同次座標とおなじみの座標を結びつける関係式は以下のように表される。
x_{Euc}=\frac{X_{Hom}}{Z_{Hom}}\\
y_{Euc}=\frac{Y_{Hom}}{Z_{Hom}}\\
本題。ここで定数倍$S$になったときの各座標の変化を見てみる。
おなじみのXYZ座標の場合。
$SP=S(x_{Euc},y_{Euc})=(Sx_{Euc},Sy_{Euc})$となり、
$P≠SP$となる。
同次座標の場合。
$SP'=S(X_{Hom},Y_{Hom},Z_{Hom}) = (SX_{Hom},SY_{Hom},SZ_{Hom})$より、
x'_{Euc}=\frac{SX_{Hom}}{SZ_{Hom}}=\frac{X_{Hom}}{Z_{Hom}}=x_{Euc}\\
y'_{Euc}=\frac{SY_{Hom}}{SZ_{Hom}}=\frac{Y_{Hom}}{Z_{Hom}}=y_{Euc}\\
したがって、$SP=P$。
同次座標の場合、座標が不変であることがわかる。
不変。これの何が便利かといえば、
例えばとある同次座標$E$があった時、
定数倍された$sE$は変わらないはずなので、$E$と同質の値となる・・・といったような
使い方ができる。(後で使う)
(5-4)世界座標から画像座標への変換
ということで、以下の式が手に入った。
\\
X_{camera}
=
\left(
\begin{array}{ccc}
X_{camera}\\
Y_{camera}\\
Z_{camera}\\
1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13} & tx\\
r_{21} & r_{22}& r_{23} & ty\\
r_{31} & r_{32}& r_{33} & tz\\
0 & 0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{c}
X\\
Y\\
Z\\
1
\end{array}
\right)
\\
⇔
\\
X_{camera}=[R|T]X_{world}
$[R|T]$というのは、$R$と$T$をそのまま並べていることを表している。
さて次のステップ。
上の方にてカメラ座標を画像のピクセル座標に変換する式を下記の様に示した。
X_{image} = KX_{camera}
これに先程の式を組み込むと以下のようになる。
X_{image} = K[R|T]X_{world}
これこそが今一番求めたかった式。
画像のピクセル座標をそのままダイレクトに世界座標に変換できる式。
世界座標は三次元の座標であるので、この式さえ求まれば
画像のピクセルを三次元座標に変換することができるのである!
$K[R|T]$と射影行列$P$とよぶ!
P=K[R|T]
【参考】
http://web.wakayama-u.ac.jp/~wuhy/CV09.pdf
(5-5)基本行列Eからカメラ姿勢の推定・・・の前に
①「基礎行$E$がわかれば、三次元座標がわかる!」←いまここ
↓
②「$F$がわかれば、$E$がわかる!」←←ok
↓
③「$X$と$XR$がわかれば、FFがわかる!」←ok
↓
④「画像のピクセルの座標がわかれば、$X$と$XR$がわかる!」←ok
ということで、三次元座標の求め方はわかったので、
これを適用させてみよう!
とりあえずわかった情報を並べてみる!
P=K[R|T]
この式を使えば三次元座標がわかる!
$K$は上述の通りExif情報さえわかれば既知になるので、
$R$と$T$さえ当てはめればOK!
E=K^{T}FK
これが長い工程を経てようやく既知になった式!
この式から$P=K[R|T]$を適用させればそれで終わりである!!!!
・・・。
どうやって基本行列$E$から回転行列$R$と移動行列$T$を求めればいいんだ・・・?
結論から言えば、$E$から$R$と$T$を導かなければ行けない。
このページはいつになったら終わるのだろう・・・。
(5-6)基本行列から回転行列と移動行列を抽出する
外積を内積に変換
もはや随分昔の話であるが、$E$は下記の式で求められていた。
E=T×R
これを別の形に書き換えてみる。
E=
\left(
\begin{array}{ccc}
tx\\
ty\\
tz
\end{array}
\right)
×
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13}\\
r_{21} & r_{22}& r_{23}\\
r_{31} & r_{32}& r_{33}\\
\end{array}
\right)\\
⇔
\\
E=
\left(
\begin{array}{ccc}
0 & -tz & ty\\
tz & 0 & -tx\\
-ty & tx & 0
\end{array}
\right)
\left(
\begin{array}{ccc}
r_{11} & r_{12}& r_{13}\\
r_{21} & r_{22}& r_{23}\\
r_{31} & r_{32}& r_{33}\\
\end{array}
\right)\\
\\
⇔
\\
E=SR
外積を内積に置き換えると上記のように書き換えることができる。
$S$を交代行列・歪対称行列(skew-symmetric matrices)と呼ぶ。
基本知識8 歪対称行列の性質
歪対称行列の性質は以下の通り。
(0)歪対称行列はどんな行列?
行列を対角線上で2つに分けて見たときに、
対角線を堺に正負の値がまるっと反対になっている行列である。(ざっくり)
上の方にある行列$S$を見ればイメージは伝わると思う。
(1)$S$が歪対称行列なら、$S^{T}=-A$が成立する。
(2)以下のような$Z$があったとする。
Z=
\begin{eqnarray}
\begin{pmatrix}
k_{1}B & & & & & &0\\
& k_{2}B & & & & & \\
& & \ddots & & & & \\
& & & k_{n}B & & & \\
& & & & 0 & & \\
& & & & & \ddots & \\
& & & & & & 0 \\
0 & & & \sigma_{ 9 }
\end{pmatrix}
\end{eqnarray}\\
\\
B=
\left(
\begin{array}{ccc}
0 & 1 \\
-1 & 0 \\
\end{array}
\right)
$Z$のなかにある$B$には、定義した行列がそのまま入る。
行列の中に行列を持つ行列。このような行列を区分行列という。
このとき、$U$を任意の直交行列(上述の基本知識参照)とすると以下の式が成立する。
S=UZU^{T}
(証明は
http://cvrs.whu.edu.cn/downloads/ebooks/Multiple%20View%20Geometry%20in%20Computer%20Vision%20
(Second%20Edition).pdf P581)
このままだとどうにもわかりづらいので、
$Z$に内在するパラメータ$k$のうち、$k_{1}$まで存在するときの行列$Z$を書き下す。
Z_{1}=
\left(
\begin{array}{ccc}
k_{1}B & 0 \\
0 & 0 \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 0 \\
\end{array}
\right)
よって$S$は以下のようにあらわされる。(以降で使います。)
S=UZU^{T}=U\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 0 \\
\end{array}
\right)U^{T}
基本行列Eの特異値は2つ同じで1つは0の性質
ここまでは情報の整理と基本知識。
以降は$E$から回転行列$R$と移動行列$T$を求めるための内容について記載する。
復習。$E=K^{T}FK$の式より、$E$の具体的な値を求めた。
ここから回転行列$R$と移動行列$T$を求めたいが、さてどうしよう。
とりあえず困ったときの特異値分解。
$E$を特異値分解してみる。
E=UΣV^{T}
さてこのとき。
証明はこの項の下の方で基本知識として記載している(予定)であるが、
$E$の性質として、「$E$の特異値は同じ値が2つとゼロの特異値1つをもつ」という性質を持っている。
(“Motion from Point Matches : Multiplicity of Solutions,”
https://hal.inria.fr/inria-00075401/document P7 Proposition 2)
SVDの基本知識で述べたとおり、$Σ$は対角線上に特異値という値が並ぶことを述べた。
この性質より以下のように$Σ$を表現できる。
Σ=
\left(
\begin{array}{ccc}
s & 0 & 0\\
0 & s & 0\\
0 & 0 & 0\\
\end{array}
\right)
$s$は特異値を表し、先ほどの性質が表されていることがわかる。
これを先程の式に組み込むと、
E=sU
\left(
\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0\\
\end{array}
\right)
V^{T}
\\
⇔
\\
E=U
\left(
\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0\\
\end{array}
\right)
V^{T}
ここで、$Σ$から特異値$s$を行列の外に出してちゃっかり$s$を消してしまっている。
理由としては、各専門書いわく「基本行列$E$のスケールは任意であるため。」
やたらと"up to scale"という単語が頻出する。
この意味するところは、
「$E$は同次座標だから定数倍しても影響ないよ」ということを指す。
よって、$E=sE$とおけるので最終的には下記式となる。
E=U
\left(
\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0\\
\end{array}
\right)
V^{T}
Eの式を変形させる
次に、$E=UΣV^{T}$を以下のように式変形させる。
E=UΣV^{T}=UWΣU^{T}UW^{-1}V^{T}
なお、$W$は下記式である。
W=
\left(
\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0\\
0 & 0 & 1
\end{array}
\right)
長い式だ。上式が本当に成立するかどうか展開して確認してみる。
$U^{T}U=I$、$AI=I$より以下のように展開される。
UΣV^{T}=UWΣU^{T}UW^{-1}V^{T}=UWΣW^{-1}V^{T}
各項の値を実際に計算してみる。
WΣ=
\left(
\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0\\
0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0\\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
0 & -1 & 0\\
1 & 0 & 0\\
0 & 0 & 0\\
\end{array}
\right)
WΣW^{-1}=
\left(
\begin{array}{ccc}
0 & -1 & 0\\
1 & 0 & 0\\
0 & 0 & 0\\
\end{array}
\right)
\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0\\
0 & 0 & 1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0\\
0 & 0 & 0
\end{array}
\right)
=Σ
よって、$WΣW^{-1}=Σ$が求まるので、下記式が成立する。
UWΣU^{T}UW^{-1}V^{T}=UWΣW^{-1}V^{T}\\
UWΣW^{-1}V^{T}=UWΣW^{-1}V^{T}\\
UWΣW^{-1}V^{T}=UΣV^{T}\\
⇔\\
E=UWΣU^{T}UW^{-1}V^{T}
ということで、$E$が$E=UWΣU^{T}UW^{-1}V^{T}$で表されることが分かった。
Eの式より回転行列Rと歪対称行列Sを抽出する
$E=UWΣU^{T}UW^{-1}V^{T}$の式を手に入れた。
次に、この式のいち部分である$WΣ$に着目する。
さきほど、$WΣ$の中身を以下のように計算した。
WΣ
=
\left(
\begin{array}{ccc}
0 & -1 & 0\\
1 & 0 & 0\\
0 & 0 & 0\\
\end{array}
\right)
\\
ここでとある行列$Z$を以下のように定義する。
Z=
\left(
\begin{array}{ccc}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 0\\
\end{array}
\right)
「基本知識8 歪対称行列の性質」より、
$WΣ$は歪対称行列に分類される行列であることがわかる。
歪対称行列の性質より、$(WΣ)^{T}=-WΣ$となる。
したがって、
(WΣ)^{T}
=-WΣ
=-1)
\left(
\begin{array}{ccc}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 0\\
\end{array}
\right)
=-Z
\\
⇔
\\
WΣ=Z
これにより、$WΣ$は行列$Z$で表せた。
ここで思い出してほしいのは、「基本知識8 歪対称行列の性質」の知識である。
「基本知識8 歪対称行列の性質」の(2)では、歪対称行列$S$は以下の行列で表されることを示した。
S=UZU^{T}=U\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 0 \\
\end{array}
\right)U^{T}
そして奇しくも、
先程の$Z$をつかうことで、$E=UWΣU^{T}UW^{-1}V^{T}$より$S$を見出すことが可能である。
E=UWΣU^{T}UW^{-1}V^{T}\\
E=UZU^{T}UW^{-1}V^{T}\\
E=SUW^{-1}V^{T}
次に$S$以外の項を$R$とおけば、以下の式が求められる。
R=UW^{-1}V^{T}\\
S=UZU^{T}\\
⇔\\
E=SR
ここでは一旦、この式の$R$と$S$を求めたい回転行列と移動行列の歪対称行列とみなす。
あくまで仮説として、$E=SR$と同義であると仮定する。(後で証明フェーズがあります)
仮設ではあるが、ひとまずは仮$R$と仮$S$を求めることに焦点当てる。
まずは$R$について。
$W^{-1}$を展開すると、$R$は下記のように整理される。
R=UW^{-1}V^{T}\\
R=U
\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)U^{T}
先程計算した$W^{-1}$。
実はこの行列は、Z軸方向に90度回転させるときの回転行列$r$と一致するのである。
Z軸方向に回転させるときの公式とともに記載すると、
r_{z}=
\left(
\begin{array}{ccc}
cosθ & -sinθ & 0 \\
sinθ & cosθ & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\\
⇔
\\
r_{z90°}=
\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\\
⇔
\\
W^{-1}=r_{z90°}
上記より、$W^{-1}=r_{z90°}$の関係式が得られた。
したがって、$R$は以下のようにあらわされる。
R=UW^{-1}V^{T}\\
⇔\\
R=Ur_{z90°}V^{T}\\
また、$W^{-1}$は他にも表現できる。
r_{z}=
\left(
\begin{array}{ccc}
cosθ & -sinθ & 0 \\
sinθ & cosθ & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\\
⇔
\\
r_{z-90°}=(-1)
\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
今度は-90度に回転させる回転行列。
したがって、$R$は下記の書き方でも表現できる。
R=UW^{-1}V^{T}\\
⇔\\
R=-UWV^{T}\\
⇔\\
R=Ur_{z-90°}V^{T}\\
以上をまとめると、
$R$は2通りのパターンが存在することになる。
\left\{
\begin{array}{lll}
R=Ur_{z90°}V^{T}\\
R=Ur_{z-90°}V^{T}\\
\end{array}
\right\}\\
⇔\\
\left\{
\begin{array}{lll}
R=UW^{-1}V^{T}\\
R=-UWV^{T}\\
\end{array}
\right\}\\
したがって、$R$と$S$は以下の2パターンが存在することになる。
S_{1}=UZU^{T}
, R_{1}=UW^{-1}V^{T}\\
or
\\
S_{2}=UZU^{T}
,R_{2}=-UWV^{T}\\
$U$と$V$は$E$の特異値分解で既に求まっており、
$Z$と$W$は自分で定義した行列なのでもちろん既知。
よって、$S$と$R$の各パターンを計算できることがわかる。
本当にこれは回転行列Rと歪対象行列Sなの?
これにより、$E=RS$の数式化に成功した。…とする前に、一つ証明を行わなければならない。
それは、ここで求めた$S,R$が本当に求めたい行列なのかどうかを確かめることである。
今少なくとも判明している点は、
(1)$S$が歪対象行列であるということ
(2)$R$が回転行列ということ。
$S,R$は最低限これらの条件を満たす必要がある。
よって、以下の点を証明する必要がある。
(1) 「$S$が歪対象行列であるかどうか ⇔ $A^{T}=-A$になるかどうか」
(1-1)「$R$が回転行列であるか ⇔ $A^{T}A=I$ 」
(1-2)「$R$が回転行列であるか ⇔ $det|A|=1$になるか」
(1)(1-1)は線形代数の知識で解けるので興味のある人は
http://www.maths.lth.se/media11/FMA270/2017/forelas6.pdf
「3 Computing Cameras from E」を参照。
(1-2)についてだが、
計算過程は割愛するが、(3)を満たすには、$det|UV^{T}|=1$を満たさなければいけない。
$U$と$V$は$E$を特異値分解して生まれたものなので、
$E$がノイズの影響を受けていた場合には$U$と$V$もノイズの影響をうける。
理論的には、$det|UV^{T}|=1$を満たさない場合には、$R$が回転行列にはならないことに注意したい。
($det|UV^{T}|=-1$のときは、R=-R、t=-tとみなす。)
歪対象行列Sから移動行列Tの導出
$S,R$は計算できそう。
ところで$S$ってなんだっけ・・・?
次に考えなければならない問題は、本来の移動行列$t$を求めることである。
とりあえず、$S$は既知なので$S$と$T$の関係式を求めてみる。
$S,t$は$S$を導出したときとは逆に、
内積から外積に変換することで$S$と$t$は以下のような式で表せる。
St=t×t=0
\\
⇔
\\
St=0
$St=0$。同次形である。
いくつかの解説サイトでは、$St=0$から解$t$を求めていたが、
なんの説明もなくいきなり解$t$を記載する場合がほとんどで、計算過程が謎であった。
https://www.slideshare.net/phani279/lecture-9h
上記サイトでは、経験的に解を推測し、
その解が$St=0$が当てはまることを確認していた。
そのやり方はあまり解析的ではないので、別の証明の流れに則る。
https://ja.coursera.org/lecture/robotics-perception/epipolar-geometry-iii-Bwk0d
せっかく書いた$St=0$だが、この式は使わない。
$E$と$t$は、$E$の性質により$E^{t}t=0$の等式を得るのでこれを利用して$t$を推定する。
E^{t}t=0
なお、この等式が成立することの証明は下の方に書いている(予定)のでそちらを参照。
$S$と違って$E$であれば既に特異値分解を行っているので、
「特異値分解の性質(後述)」を利用することができるのが強い。
$E^{t}t=0$。
これまで$Ax=0$という形式の等式は扱ってきたが、
それとは形式が異なることが見てわかる。
$E^{t}t=0$の式は$A^{T}x=0$の形式に該当する式であり、
この時の$x$を左零空間(left null space / left nullspace)と呼ぶ。
この手の方程式でとても強力なのが特異値分解である。
特異値分解の基本知識の項において、$Ax=0$の解について
「$A=UΣV^{T}$と特異値分解SVDしたときの直交行列$V$のうち、
$Σ$の特異値が0になる箇所に該当する$V$の列ベクトルで表すことができる。」
と記載した。
同様に、
$A^{T}x=0$についても特異値分解の一部の行列から解を簡単に見出すことができるのである。
ということで、$A^{T}x=0$の「左零空間」と特異値分解の関係についてもう少し見てみる。
【参考】
https://ja.coursera.org/lecture/robotics-perception/epipolar-geometry-i-oNHO9
基本知識9 特異値分解その2 部分空間と特異値分解について
以前、別の特異値分解の基本知識の項にて、
とある行列$A$のランクを$r$としたとき、
$Ax=0$の解はVの列ベクトル$v_{r+1}$~$v{n}$であることを述べた。
よって解xは以下のようにあらわされる。
x=c_{r+1}v_{r+1}+c_{r+2}v_{r+2} + \cdots + c_{n}v_{n}
$c$はパラメータ。ここにはどんな値が入っても解として成立することを表している。
このように、Ax=0を満たす解がとりうるベクトルの集合を「零空間」という。
そして実は、特異値分解は$Ax=0$以外にも解を求めることができる。
具体的には、列空間、行空間、左零空間の解を求めることができる。
それぞれの用語の意味も含めて以下に分類する。
(1)Aの列空間 ⇒ 特異値分解のUの列1~列rankAのベクトルで表せる
そもそも列空間とは
行列$A$が$A=(a_{1},a_{2},\cdots,a_{n})$の列ベクトルで構成されていた時。
以下の式で全ての列ベクトルが表せるとする。
VC = v_{1}c_{1}+v_{2}c_{2}+\cdots+v_{r}c_{r}
パラメータ$c$(定数)に適切に値を入れれば、上記式は必ずすべての$A$の列ベクトルを表現する。
また、パラメータ$c$には無限の定数が入るので相当なベクトルが表現される。
このように、$VC$が生成し得る全てのベクトル集合を列空間と呼ぶ。
パラメータ(次元)について
以下ちょっとだけ復習。
次元とは、解がいくつのパラメータで表せるかを示す値である。
復習として、以前ランクの基本知識で記載した行列$A$をそのまま書く。
AX=0
\\
⇔
\\
AX=
\left(
\begin{array}{c}
1 & 0 & 2\\
0 & 1 & -3 \\
\end{array}
\right)
\left(
\begin{array}{c}
x \\
y \\
x
\end{array}
\right)
=0\\
⇔
X=
\\
\\
\left(
\begin{array}{c}
x \\
y \\
z
\end{array}
\right)
=
a
\left(
\begin{array}{c}
-2 \\
3 \\
1 \\
\end{array}
\right)
このような時、解$x$は$(-2,3,1)^{T}$の定数倍分無限に発生する。
非常に今更であるが、用語を整理すると、
ここまで解と表現して記載したのは$(-2,3,1)^{T}$、
次元は$a$のような無限の数が入り得るパラメータの数を指している。
$Ax=0$では、この次元の数を(変数の個数)-(Aのランク数)で計算できることを
ランクの基本知識の項で記載した。
上記の例では、xyzの変数が存在するので(変数の個数)=3。
そして(Aのランク数)は別途SVDなり階段行列なりで計算すると2となるので、
(変数の個数)-(Aのランク数)=3-2=1.
よって次元は1であるので、上記の$A$はパラメータ$a$一つだけで表すことができた。
・・・
・・
・
復習終わり。
$Ax=0$の解$x$が取り打つベクトルの集合、「零空間」では
上記の通り(変数の個数)-(Aのランク数)で次元、もとい解がいくつのパラメータで表現されるか決定される。
一方、列空間では次元が零空間と異なる。
列空間では、(Aのランク数)が次元となる。
実例としては、
A=(a_{1},a_{2},a_{3},a_{4})\\
a_{1}=
\left\{
\begin{array}{lll}
-1 & 2 & 1\\
\end{array}
\right\}
,
a_{2}=
\left\{
\begin{array}{lll}
1 & -1 0\\
\end{array}
\right\}
,
a_{3}=
\left\{
\begin{array}{lll}
1 & -2 &-1\\
\end{array}
\right\}
,
a_{4}=
\left\{
\begin{array}{lll}
-1 & 0 & -1\\
\end{array}
\right\}
\\
A=
\left\{
\begin{array}{lll}
-1 & 2 & 1\\
1 & -1 0\\
1 & -2 &-1\\
-1 & 0 & -1
\end{array}
\right\}
を考えたとき。行列操作を行うと(操作方法は割愛)
行列Aの任意の列$a_{1},a_{2},a_{3},a_{4}$は以下の式で表される。
v_{1}=
\left\{
\begin{array}{lll}
1\\
0\\
1\\
0
\end{array}
\right\}
\\
v_{2}=
\left\{
\begin{array}{lll}
1\\
2\\
0\\
1
\end{array}
\right\}
v_{1}c_{1}+v_{2}c_{2}=
c_{1}
\left\{
\begin{array}{lll}
1\\
0\\
1\\
0
\end{array}
\right\}
+
c_{2}
\left\{
\begin{array}{lll}
1\\
2\\
0\\
1
\end{array}
\right\}
上記の式で、すべての列ベクトル$a_{1},a_{2},a_{3},a_{4}$が表現される。
パラメータには制約なく様々な値が入り得て、
上記の式で表現され得る全てのベクトルの集合を列空間と呼ぶ。(さっき言った)
さて、次元についてだが、
rankAの値は階段行列やらSVDで2であることを求めることができる。
2つのパラメータで表現されているので次元数は2。
したがって、rankA=2と一致することも確認できた。
列空間と特異値分解の関係
さてそれでは$v$はどのように求められるだろう。
ガウスの前進消去などの手法があるが、ここでは特異値分解による求め方を記載する。
まず、$A=UΣV^{T}$として中身を以下のように展開したとする。
($U$はm×m、$Σ$はm×n、$V$はn×m)
A=
\left(
\begin{array}{c}
a_{11} & \cdots & a_{1n}\\
\vdots & \cdots & \vdots\\
a_{m1} & \cdots & a_{mn}\\
\end{array}
\right)
=(u_{1} u_{2} \cdots u_{r} \cdots u_{n})
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
& & & \sigma_{ r } \\
0 & & & & 0
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{c}
v_{1}^{T} &
v_{2}^{T} &
\cdots &
v_{r}^{T}
\cdots &
v_{n}^{T}
\end{array}
\right)
\\
このとき、列空間をなす列ベクトル$v$(基底)は
$u_{1}$~$u_{r}$と一致する性質をもつのである。
これにより、特異値分解の$U$の列1~列rankAから列空間の基底を導いた。
以下ここまでのまとめ。
●$A$の列空間は$A$の列ベクトルすべてを表現するベクトルの集合を意味する。
●$A$の列ベクトルの集合は
$v_{1}c_{1}+v_{2}c_{2}+\cdots+v_{r}c_{r}$
のようにあらわされる。
このベクトルの表すベクトルはすべての$A$の列ベクトルを表現する。
●列空間の次元($vc$の項の数)は$A$のランクによって決定される。(零空間とは違う)
●列空間をなす列ベクトル$v$(基底)は
$A$のランクを$r$、$A=UΣV^{T}$と特異値分解をし、$U=(u_{1} \cdots u_{n})$を得たとすると、
$v_{1}$~$v_{r}$は$u_{1}$~$u_{r}$と一致する。
(2)Aの行空間 ⇒ 特異値分解のVの列1~列rankAのベクトルで表せる
本ページにはあまり関係ないので省略して記載する。
行空間は列空間の行バージョンであるので、列空間と大体似たような感じに表される。
(行空間をなす行ベクトル$r$が特異値分解の$V$で表されていることに注意する。)
●$A$の行空間は$A$の行ベクトルすべてを表現するベクトルの集合を意味する。
●$A$の行ベクトルの集合は
$r_{1}c_{1}+r_{2}c_{2}+\cdots+r_{r}c_{r}$
のようにあらわされる。
このベクトルの表すベクトルはすべての$A$の行ベクトルを表現する。
●行空間の次元($rc$の項の数)は$A$のランクによって決定される。(零空間とは違う)
●行空間をなす行ベクトル$r$(基底)は
$A$のランクを$r$、$A=UΣV^{T}$と特異値分解をし、$V=(b_{1} \cdots b_{n})$を得たとすると、
$r_{1}$~$r_{r}$は$b_{1}$~$b_{r}$と一致する。
(3)Aの左零空間 ⇒ 特異値分解のUの列1~列rankAのベクトルで表せる
列空間、行空間とはちょっとだけイメージが違うかもしれない。
ちょっと復習する。
$Ax=0$の$x$に入るベクトルの集合を零空間と呼ぶ。
復習終わり。これに対して、
$A^{T}x=0$の$x$に入るベクトルの集合を左零空間と呼ぶ。
定義は以上。割とシンプルである。
パラメータ(次元)について
次元の意味などは(1)列空間を参照。
零空間では(変数の個数)-(Aのランク数)がパラメータの数であった。
(変数の個数)というのは、$Ax=0$のうちの$x$の中の未知数の数を指していた。
これを具体的に言えば、Aの行数が(変数の個数)となることに注意したい。
これを言い換えれば、
「零空間の次元は(Aの行数)-(Aのランク数)が次元数となる」
となる。
これに対して左零空間の場合、
左零空間は$A^{T}x=0$の式で表されるが、
言い換えればこれは$A^{T}$の零空間ともいえる。
よって、先ほどの零空間の関係に当てはめようとすると、
($A^{T}$の行数)は転置によって($A$の列数)とみなすことができるので
「左零空間の次元は($A$の列数)-(Aのランク数)がパラメータの数、もとい次元数。」
となる。
まとめると以下の通り。
(1) 零空間の次元は($A$の行数)-(Aのランク数)がパラメータの数
(2)左零空間の次元は($A$の列数)-(Aのランク数)がパラメータの数
左零空間と特異値分解の関係
以下のように$A$を特異値分解したとする。
($U$はm×m、$Σ$はm×n、$V$はn×m)
A=
\left(
\begin{array}{c}
a_{11} & \cdots & a_{1n}\\
\vdots & \cdots & \vdots\\
a_{m1} & \cdots & a_{mn}\\
\end{array}
\right)
=(u_{1} u_{2} \cdots u_{r} \cdots u_{n})
\begin{eqnarray}
\begin{pmatrix}
\sigma_{ 1 } & & & & 0 \\
& \sigma_{ 2 } & & \\
& & \ddots & \\
& & & \sigma_{ r } \\
0 & & & & 0
\end{pmatrix}
\end{eqnarray}
\left(
\begin{array}{c}
v_{1}^{T} &
v_{2}^{T} &
\cdots &
v_{r}^{T}
\cdots &
v_{n}^{T}
\end{array}
\right)
\\
このとき、左零空間の解$x$(基底)は
特異値が0になる添え字の$U$の列ベクトル、
すなわち、$u_{r+1}$~$u_{n}$が左零空間の解$x$になる。
A^{T}x=0
\\
⇔
\\
x=u_{r+1}c_{r+1}+\cdots+u_{n}c_{n}
($c$はパラメータ)
【参考】
http://roboticstips.web.fc2.com/index/mathematics/subspace/subspace.html
https://ja.wikipedia.org/wiki/%E7%B7%9A%E5%9E%8B%E4%BB%A3%E6%95%B0%E5%AD%A6%E3%81%AE%E5%9F%BA%E6%9C%AC%E5%AE%9A%E7%90%86
同次形E^{T}t=0の導出
書く予定。
書き忘れてたらすみません
左零空間より解tを導く
さて本題。
方針としては、$E^{t}t=0$から解$t$を求める事。
先ほどの特異値分解の基本知識では、$A^{t}x=0$のときの左零空間について記載したが、
$E^{t}t=0$はまさに$A^{t}x=0$の形式に合致する。
$E=UΣV^{T}$
ということで、特異値分解を利用して$E^{t}t=0$の解を求める。
$E$はすでに特異値分解を実行済みである。
$E$の性質より、特異値が2つ存在することを既に述べた。
特異値分解の基本知識にて、特異値がランクの数と同じであることを述べたが
それに当てはめると、$E$のランクは2となることがわかる。
rankE = 2
ここで、先ほどの特異値分解の基本知識に書いた内容を復習する。
特異値分解の基本知識の項では、$A^{t}x=0$を満たす解$x$について、
「特異値が0になる添え字の$U$の列ベクトル、
すなわち、$u_{r+1}$~$u_{n}$が左零空間の解$x$になる。」と述べた。
$n$とは、$A^{t}x=0$における行列$A$の列の長さ。
$r$とは、$A$のランク。
これを$E$に当てはめれば$n=3$,$r=2$
よって、求める解$t$は以下のようになる。
t=u_{3}
基本行列の4つの可能性
上の説明のどこかで、$E$は同次座標であるためスケールが不変であることを述べた。
同次座標。$sE$(sは定数)は$E$の同等に表現されるというやつである。
E=sE
これはもちろん、$(-1)$をかけた場合でも適用される。
E=-E
$E$のもとの式である$E=t×R$を考えたとき、
移動行列$t$の向きによってはマイナスを取る場合も当然あるわけだが、
同次座標の影響により、正負の区別がなくなってしまう。
したがって、$t$が取り得る可能性として、以下の2つが存在する。
$t=-u_{3}$ or $ u_{3}$
回転行列は上述の通り2通りのパターンがあることを触れた。
$R=UW^{-1}V^{T}$ or $UWV^{T}$
$E$は$E=t×R$で表されるので$t$と$R$で構成されている。
したがって、$E$は2×2=4パターンの可能性が存在することになる。
果たしてどれが有効な$E$であるかを見極めなければならない。
これを射影行列に当てはめれば以下の4つとなる。
P=K[R|T]
\\
⇔
\\
P_{1}=K[UWV^{T} | u_{3}]\\
P_{2}=K[UWV^{T} | -u_{3}]\\
P_{3}=K[UW^{-1}V^{T} | u_{3}]\\
P_{4}=K[UW^{-1}V^{T} | -u_{3}]\\
上述の通り、射影行列はスーパーめちゃすごい行列。
この行列さえわかれば、画像のピクセル座標から世界座標の三次元座標が求め放題。
どれが正解の射影行列だろうか?
【参考】
http://www.maths.lth.se/matematiklth/personal/calle/datorseende13/notes/forelas6.pdf 3 Computing Cameras from E
https://en.wikipedia.org/wiki/Essential_matrix
https://www.mia.uni-saarland.de/Teaching/MFCV11/skript-mfcv.pdf Theorem4.2.3
http://users.cecs.anu.edu.au/~hartley/Papers/Q/Q.pdf
(6)三次元座標の推定
(6-1)ノイズを考慮した三次元座標の算出
当たり前のことだがカメラはカメラの前にあるものしか撮影できない。後ろにレンズはついてない。
したがって、
「生成された三次元座標は2つのカメラの前にないといけない」
という制約条件を見出すことができる。
4つの射影行列を使えば、三次元座標を計算することができるわけだが、
上記の制約条件を利用することで明らかに誤りのある射影行列を取り除くことができる。
よって、以下の処理を行うことで4つの誤った射影行列から正しい射影行列を導き出す。
①4つそれぞれの射影行列を用いて、それぞれの三次元座標を計算する
②三次元座標とカメラの位置を見て、
三次元座標がカメラの前に存在する射影行列を正とする。
三次元座標の計算は、射影行列を用いれば容易に計算できることを以前述べた。
「完璧に測定された射影行列」であれば、以前に説明した下記式で求められる。
x_{image} = PX_{world}
「完璧に測定された射影行列」であれば、これを使って計算すればそれで終わり。
しかしここで取り扱うのは実際の現実のデータ。
しかもここまで、何度もノイズ除去のために推定してきた数値をもとに算出した射影行列。
ノイズの影響を受けることが容易に想像できる。
必要なのは、「射影行列を用いたノイズに頑強な三次元座標の推定方法」。
基礎行列$F$を推定する際には、8点アルゴリズムによりノイズに強い手法で
推定を行ったが、似たような感じで三次元座標を求められないだろうか?
(6-2)三角測量の利用
基礎行列$F$を算出す際には、$F$を$x$と置いて
$Ax=0$という関係式を導き出すことで解$x$を導き出した。
とりあえずの方針として、
4つの射影行列と三次元座標$x$に関する等式を導き出し、
$Ax=0$の形式を見出すことを目標に考えてみる。
以前、射影行列と三次元座標の関係式を以下のように示した。
画像のピクセル座標を$x_{image}$、三次元座標を$X_{world} $とすると、
下記の式が導かれることを射影行列に関する項で説明した。
x_{image} = PX_{world}
上記の式より、x_{image}とPX_{world}は同じもののはずである。
外積は同じもの同士だと必ず0になることから、以下の等式が得られる。
x_{image}×PX_{world} =0
さてこの式。
$A=x_{image}×P$とみなせば、$AX_{world}=0$という式になる。
これにより、求めたかった$Ax=0$の同次形の関係式がぼんやりと浮かび上がってくる。
とりあえず$A=x_{image}×P$の中身を展開してみよう。
以下のように$x_{image}$と$P$を置いたとする。
($P$は$K[R|T]$より$K$が3×3、$[R|T]$が3×4より3×4となる。)
x_{image}
=
\left(
\begin{array}{c}
x \\
y \\
\end{array}
\right)
,
P=
\left(
\begin{array}{c}
p_{11} & p_{12} & p_{13} & p_{14}\\
p_{21} & p_{22} & p_{23} & p_{34}\\
p_{31} & p_{32} & p_{33} & p_{34}\\
y \\
\end{array}
\right)\\
⇔\\
\left(
\begin{array}{c}
p_{1r}^{t} \\
p_{2r}^{t} \\
p_{3r}^{t} \\
y \\
\end{array}
\right)\\
これを$A=x_{image}×P$で展開すると
最終的には以下の通りになる。
A=
\left(
\begin{array}{c}
yp_{3r}^{t} - p_{2r}^{t} \\
p_{1r}^{t} - xp_{3r}^{t}\\
y \\
\end{array}
\right)\\
⇔\\
AX=0
これにより、「とある一つのカメラ」からの三次元座標$X$と$A$を導けた。
さてここで、最初のほうで述べたエピポーラ幾何の三角形の図を思い出してほしい。
2つのカメラに同じポイントが映っていれば、三次元座標$X$は同じになることを
エピポーラ幾何の三角形の図では示した。
よって、「別のカメラ」に「とある一つのカメラ」と同じものが映っていれば、
三次元座標$X$は全く同質のものになるはずである。
したがって、$A$は以下のように書くことができる。
x_{image1}
=
\left(
\begin{array}{c}
x_{1} \\
y_{1} \\
\end{array}
\right)\\
x_{image2}
=
\left(
\begin{array}{c}
x_{2} \\
y_{2} \\
\end{array}
\right)
⇒
\left(
\begin{array}{c}
y_{1}p_{3r}^{t} - p_{2r}^{t} \\
p_{1r}^{t} - x_{1}p_{3r}^{t}\\
y_{2}p_{3r}^{t} - p_{2r}^{t} \\
p_{1r}^{t} - x_{2}p_{3r}^{t}
\end{array}
\right)
X =
\begin{array}{c}
0\\
0\\
0\\
0\\
\end{array}
\right)
これにより、$Ax=0$の形式を導き出すことができた。
三次元座標の算出 ⇒ 8点アルゴリズムと同じようにいけるのでは?
やりたいことを改めて繰り返す。
$AX=0$の三次元座標$X$を求める事。
加えて、ノイズにたいして頑強な方法で求める事。
$x=PX$より、画像のピクセル座標$x$に対して真なる射影行列を使うことで
簡単に三次元座標$X$を求めることができるが、射影行列がノイズの
影響を受けていることを考えると、この式は容易には使えない。
・・・ということを踏まえて、
$x=PX$とは違う別の求め方を考えようぜ。ということで$AX=0$を導出した。
復習と整理終わり。
ということで$X$を求めよう。
この時点で求めた$A$はノイズが混じっている。
そもそも、$AX=0$になる解が本当にあるの?という疑問がある。
そこで、下記の考えを導入する。
「どうせ$AX=0$をきれいに満たす解なんてないんだから、
$AX≒0$みたいな限りなく0に近づける解$f$を探そうぜ」
$AX$を0に近づける$f$、すなわち$AX$が最小値となる$f$を求めることに注力する。
とりあえずは、ベクトルで比較すると正負の向きの影響を受けるので、
単純な大きさを比較するために絶対値の時の最小値を求めることを方針に掲げてみる。
|AX|=min
右辺のminというのは、最小値を求めますよーというのを表している。
これがいわゆる「最小絶対値法」である。
これに対して、より一般的でポピュラーなのが「最小二乗法」。
|AX|^{2}=min
一般的には「最小二乗法」のほうが評価が高いけど、
場合によっては「最小絶対値法」のほうがいいこともあるらしい・・・?
そのうち調査してみたいところではあるけど、ここでは一旦やらないでおく。
このページでは、一般的な$F$の推定に用いられる「最小二乗法」のほうを採用して以下に記載する。
・・・
・・
・
ここまでコピペ。
デジャブを感じた人は私の冗長で長い文章をちゃんと読んでる人です。いつもありがとうございます。読みづらい文章ですみません。
|AX|^{2}=min
上記の式を出すまでの説明、
実は基礎行列$F$を求めるために使った8点アルゴリズムでも同じ説明を行っている。
8点アルゴリズムは大まかに2つのステップがあり、
①最小二乗法より$Ax=0$の解$x$を求める。
②$x$のランクが既知であることを利用して$x$にたいしてノイズ除去を行う。
②を行うには情報が足りていないので、行えない。
よって①だけを行うものとする。
8点アルゴリズムで最終的に求まる解は、
$A=UΣV^{T}$とすると、最小の特異値に対応する$V$の列ベクトル。
すなわち、$V$の列ベクトルが端っこの物。
したがって、三次元座標$X$は$V=(v_{1},v_{2},v_{3})$のうち、端っこの$v_{3}$となる。
X=v_{3}
【参考】
http://www.cs.cmu.edu/~16385/s17/Slides/11.4_Triangulation.pdf
https://ja.coursera.org/lecture/robotics-perception/epipolar-geometry-iii-Bwk0d
(6-3)カメラ姿勢の推定
ここまでの手法で三次元座標の推定が行える。
さて、話を本題に戻すと、現在射影行列の候補として4つが存在する。
そして、さきほどの三次元座標の推定方法では、
1つの射影行列と、画像1のピクセル座標、画像2のピクセル座標を
入力値として与えることで最終的に三次元座標を推定した。
よって、ある1組のピクセル座標のマッチングに対して
4つの射影行列をもとに三次元座標を推定すれば、4つの三次元座標が推定されることとなる。
あとはこの座標がカメラの前にあるかどうかを見て、
どの射影行列が正しいか推定すれば良い。
・・・座標がカメラの前にあるかどうかってどうやったらわかるんだ?
OpenMVGというSfMのオープンソースでは、
ピクセル座標$x_{image}$、回転行列$R$、移動行列$t$、三次元座標$X$と置いたとき、
以下の値を満たす時にカメラが前にあると判断している。
x_{image1} \cdot (R_{1}(X+R_{1}^{T}t_{1})) > 0
x_{image2} \cdot (R_{2}(X+R_{2}^{T}t_{2})) > 0
すみません。なんでこの式がカメラが前にあることの証明になるかはわかっていないです。(汗)
別の判断方法として、下記式も有効なようです。
r_{3}(X-t)>0
$r_{3}$は回転行列の3番目の行。
こっちのほうはわかりやすいですね。
ということで、以上のことから三次元座標が求まります。
どちらかというと、三次元座標はおまけでカメラ姿勢がわかることが一番強いです。
以上で三次元座標の推定方法は終わり。
ステレオカメラと区別して書こうとしたけれど、
カメラ推定のほうは普通にステレオカメラにも適用できるでしょうね。
以上。おわり。
【参考】
http://leo.ec.t.kanazawa-u.ac.jp/~nakayama/edu/file/H20_la1_final_ans.pdf
https://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-2011/ax-b-and-the-four-subspaces/the-four-fundamental-subspaces/MIT18_06SCF11_Ses1.10sum.pdf