第7回耐量子暗号とこれからの暗号技術【連載：暗号技術の基礎を学ぶ】

Last updated at 2025-12-08Posted at 2025-12-05

この記事は、 CAMPFIRE Advent Calendar 2025 の6日目の記事 の一部です。連載記事の全体は、「第0回　暗号技術の基礎を学ぶ連載記事一覧」を参照してください。

これまでの記事では、AESやRSA暗号、楕円曲線暗号など、現在広く使われている暗号技術を扱ってきました。これらの暗号は、従来のコンピュータでは解読が困難であり、現在のインターネットセキュリティの基盤となっています。

しかし、近年の量子コンピュータ技術の急速な発展により、これらの暗号技術が将来的に危殆化する可能性が指摘されています。まだ研究段階ではあり、予測の幅は大きいですが、概ね2030年〜2050年ごろには暗号解読可能な量子コンピュータ（CRQC）が実現される可能性が示されています。本記事では、量子コンピュータがもたらす脅威と、それに対抗するための耐量子暗号（Post-Quantum Cryptography, PQC）を扱います。

ただし、ここで紹介する暗号技術のベースとなる理論は、これまで紹介した暗号理論に比べてもやや難解な部分が多くあります。そのため、理論的な詳細は省き、現在どのような暗号が耐量子暗号として想定されているかを中心に紹介します。

耐量子暗号は現在最も活発に研究が進められている暗号技術の最先端分野の一つです。本記事で紹介する情報は執筆時点（2025年11月）のものであり、新たな攻撃手法の発見やアルゴリズムの安全性評価の更新など、将来的に情報が変更される可能性が十分にあります。実際のシステムへの実装を検討する場合は、最新の研究動向や標準文書を必ず確認してください。

※この記事は、文章案の作成や表現の調整、内容の検証や修正のサポート等に生成AIを利用しています。

7.1 量子コンピュータと従来の暗号への脅威
7.2 NIST PQC標準化プロジェクト
7.3 耐量子暗号への移行の課題
7.4 格子暗号（Lattice-Based Cryptography）
7.5 多変数多項式暗号（Multivariate Cryptography）
7.6 同種写像暗号（Isogeny-Based Cryptography）
7.7 符号ベース暗号（Code-Based Cryptography）
7.8 ハッシュベース署名（Hash-Based Signatures）
7.9 実世界の動向
7.10 まとめと今後の展望

7.1 量子コンピュータと従来の暗号への脅威

量子コンピュータとは

量子コンピュータは、量子力学の原理を利用して計算を行う次世代のコンピュータです。従来のコンピュータがビット（0または1）を基本単位として計算するのに対し、量子コンピュータは量子ビット（qubit）を使用し、重ね合わせや量子もつれなどの量子現象を活用します。

量子コンピュータの詳細は拙著記事等を参照してください。以下の記事では量子ゲート方式と量子アニーリング方式を説明していますが、暗号技術の解読等に影響するのは量子ゲート方式のコンピュータになります。
量子コンピューティングとは

Shorのアルゴリズムによる脅威

1994年にPeter Shorが発表したShorのアルゴリズム は、量子コンピュータ上で素因数分解と離散対数問題を多項式時間で解くアルゴリズムです。

RSA暗号への影響

RSA暗号の安全性は、大きな合成数の素因数分解の困難性に基づいています。現在、2048ビットのRSA鍵を従来のコンピュータで解読するには、数千年から数万年かかるとされています。

しかし、Shorのアルゴリズムを使用できる量子コンピュータが実現すれば、2048ビットのRSA鍵は数時間から数日で解読できる可能性があります。

以下に鍵長と計算量（対数スケール）のイメージを示します（詳細は現代暗号理論、およびFactoring integers with the number field sieve | Buhler, et al.参照）。

Shorのアルゴリズムは、これまでの素因数分解法に比べて鍵長の桁数を増やしても計算量が大きく増えないため、鍵長を安全となるサイズにしてしまうと通常の暗号化や復号化などの計算量自体も大幅に増えてしまい、現実では利用できなくなってしまいます。

楕円曲線暗号への影響

楕円曲線暗号（ECC）も同様に、楕円曲線上の離散対数問題の困難性に基づいています。Shorのアルゴリズムは楕円曲線上の離散対数問題にも適用できるため、ECDSAやECDHなどの楕円曲線暗号も量子コンピュータによって解読される可能性があります。

Groverのアルゴリズムによる脅威

Groverのアルゴリズム は、非構造化探索問題を従来のコンピュータに対して、平方根の計算量で解く量子アルゴリズムです。

対称鍵暗号への影響

AESなどの対称鍵暗号は、Grover のアルゴリズムを利用すると、鍵探索攻撃の計算量が $O(2^n)$ から $O(\sqrt{2^n}) = O(2^{n/2})$ に短縮します。
したがって AES-256（鍵長が256-bit）は、量子攻撃下では約 128-bit 相当の安全性となります。ただし、逆にこれは対称鍵暗号の鍵長を2倍（512-bit）にすることで量子攻撃下でも、現在のAES-256と同等の安全性を担保できるとも言えます（AES-256をAES-512にする）。

ハッシュ関数への影響

SHA-2などのハッシュ関数にもGroverのアルゴリズムが影響します。nビットのハッシュ値の原像攻撃や衝突攻撃も対称鍵暗号と同様に従来の計算量 $O(2^n)$ から $O(2^{n/2})$ になります。

さらに、衝突攻撃については、Brassard-Høyer-Tapp（BHT）アルゴリズムにより、 $O(2^{n/3})$ まで削減できることが示されています。
参考：Quantum Algorithm for the Collision Problem | Gilles Brassard, Peter Høyer, Alain Tapp

しかしながら、どんな量子アルゴリズムでも1/3が下限となることが証明されているため、これ以上継続して計算量が新たなアルゴリズムにより改善される可能性は現時点では低いことも示されています。
参考：Quantum lower bounds for the collision and the element distinctness problems | Yaoyun Shi

そのため、量子攻撃下で従来と同等の安全性を担保するためには、2〜3倍程度のサイズのハッシュ値にしていく必要があります。

量子コンピュータの現状

現在、実用的な量子コンピュータはまだ実現していませんが、GoogleやIBMなどの企業が数十から数百量子ビットの量子コンピュータを開発しており、量子優位性 （特定の問題で従来のコンピュータを上回る性能）の実証も行われています。

専門家の予測では、実用的な量子コンピュータが実現するのは2030年代から2040年代とされています。暗号技術の移行には10年から20年の時間がかかるため、今から準備を始める必要があります。

7.2 NIST PQC標準化プロジェクト

標準化の背景

量子コンピュータの脅威に対抗するため、米国国立標準技術研究所（NIST）は2016年にPost-Quantum Cryptography（PQC）標準化プロジェクト を開始しました。このプロジェクトの目的は、量子コンピュータに耐性を持つ暗号アルゴリズムを標準化することです。

標準化プロセスの流れ

提案段階 ：世界中の研究者から耐量子暗号アルゴリズムの提案を募集
評価段階 ：数学的安全性、実装効率性、実用性を評価
選定段階 ：最終的な標準アルゴリズムを選定
実装段階 ：標準化されたアルゴリズムの実装と展開

標準化の現状

NISTは、2022年7月に選定を発表し、2024年8月に以下を正式標準として発表しました。

ML-KEM（FIPS 203、旧CRYSTALS-Kyber） ：公開鍵暗号・鍵交換の標準として選定
ML-DSA（FIPS 204、旧CRYSTALS-Dilithium） ：ディジタル署名の標準として選定
SLH-DSA（FIPS 205、旧SPHINCS+） ：ハッシュ関数ベース署名の標準として選定

また、以下のアルゴリズムも選定されており、標準化作業が進行中です。

FN-DSA（FIPS 206、旧Falcon） ：ディジタル署名の代替標準（標準化作業中）

加えて、2025年3月にHQCの標準化が決定しました。

HQC ：符号ベース暗号による鍵カプセル化メカニズム

次セクションでは、各NISTで候補とされている各耐量子暗号技術の詳細に入る前に、耐量子暗号への移行に対する課題と、それがまさに現在直面している課題であることを説明します。

7.3 耐量子暗号への移行の課題

ここからは、個別の技術ではなく、耐量子暗号へどのように移行していく必要があるのか、そして移行期におけるセキュリティについて見ていきます。

CRYPTREC暗号技術ガイドライン（耐量子計算機暗号）2024年度版

2025年3月に公開された「CRYPTREC暗号技術ガイドライン（耐量子計算機暗号）2024年度版」は、日本における耐量子暗号の移行指針を示す重要な文書です。このガイドラインでは、耐量子暗号への移行期間の必要性と、それに伴う様々な課題について詳しく解説されています。

CRYPTREC | 暗号技術ガイドライン

移行期間が必要な理由

技術的な準備期間

PQCアルゴリズムへの移行は、単純な暗号アルゴリズムの置き換えではありません。以下の理由から、10年から20年という長期間の移行期間が必要とされます。

実装の複雑性 ：PQCアルゴリズムは従来の暗号と比べて実装が複雑で、十分なテストと検証が必要となります
標準化の進行 ：NISTの標準化プロジェクトは継続中で、完全な標準化や実用的なライブラリの実現までには時間がかかることが予想されます
相互運用性の確保 ：異なるシステム間での互換性を保証する必要があります
性能最適化 ：耐量子暗号自体は既存の暗号技術よりも一般的にパフォーマンスが出にくく、実用的な性能を実現するための最適化作業が必要となります

段階的移行の必要性

CRYPTRECガイドラインでは、以下のような段階的な移行アプローチが推奨されています。

耐量子暗号の導入にあたっては、暗号解読可能な量子コンピュータの実現時期が不透明であり、対応が必要な時期を判断することが難しいという課題があります。そのため、以下のような段階的で計画的な戦略が重要です。

1. プライオリティ設定

全ての暗号モジュールに対して、インフラ移行期間やデータ移行期間、CRQC実現までの時間の関係性を分析することは膨大な作業量となり、本当に保護が必要なデータへの対応が遅れるおそれがあります。そのため、優先度の設定、クリプト・インベントリの構築、データ管理の最適化によるPQC移行が必要なデータの適正化が求められます。
クリプト・インベントリは、各システムにおける暗号技術の利用状況を一覧化したデータベースを指し、これらにより、優先度やリスク評価に応じた、網羅的なPQC移行計画の策定を可能とします。

2. クリプトグラフィック・アジリティの確保

クリプトグラフィック・アジリティとは、暗号アルゴリズムや暗号プロトコルを迅速に変更できる性質です。アジリティを向上させることで、移行プロセスを開始するまでの猶予期間を長くすることが期待されます。アジリティを確保するためには、暗号部分が情報システムにハードコードされている状態を排除し、標準プロトコルや適切なAPI定義を利用する、ファームウェアアップデートをオンラインで実施できるように設計するなどの対策を実施することが重要です。
また、クリプトグラフィック・アジリティの評価については、成熟度モデルのCAMMや、リスク評価のCARAFなどが存在します。これらは移行計画全体の策定等への補助にもなります。

3. 既存暗号方式とのハイブリッド構成の利用

耐量子暗号への移行においては、従来の公開鍵暗号と耐量子暗号の両方を利用するハイブリッド構成が採用可能です。従来暗号と耐量子暗号の両方を同時に利用される状態にすることで、比較的新しい耐量子暗号に新たな脆弱性が見つかったとしても、従来の公開鍵暗号による保護が可能となります。

耐量子暗号への移行期間の全体像

耐量子暗号への移行は、インフラ移行期間とデータ移行期間の両方にまたがる長期的なプロセスです。以下の図は、移行期間全体の構造とその課題を示しています（Michele Mosca. 2015. Cybersecurity in a Quantum World: will we be ready? より）。

移行が安全に完了するには、解読が実現する前にインフラの移行とデータの移行の両方を実現する必要があります。量子コンピュータが実世界の暗号解読を実現できる時期は完全には予測不可能である点から、この移行作業はできる限り早く計画、実施していく必要があります。データは比較的長期にわたり保存・利用される傾向にあり、セキュリティ脅威に対する軽減策などの計画、実施が必要となる場合もあります。

ハーベスト攻撃の脅威

ハーベスト攻撃（収穫攻撃、Harvest now, decrypt laterやHNDLなどとも）は、量子コンピュータが実現する前に攻撃者が大量の暗号文を収集・保存しておき、将来量子コンピュータが実現した時点で一括解読する攻撃手法です。この攻撃は即時で解読できる必要はなく、長期間にわたって暗号文を蓄積しておき、後から解読することが可能です。

この攻撃の存在により、耐量子暗号への移行は緊急性を帯びています。一度収集された暗号文は回収不可能であり、現在進行中の通信も将来解読される可能性があるため、早期の移行準備が重要です。

耐量子暗号の候補となる暗号技術

次セクションからは、NISTが耐量子暗号として選定、標準として発表している暗号技術や、提案されている暗号技術にはいくつかの種類があります。それらについて、以降で紹介していきます。

各耐量子暗号技術の詳細よりも、実世界での導入事例等に興味がある場合は、7.9節に進んでください。

7.4 格子暗号（Lattice-Based Cryptography）

格子暗号は、格子の数学的性質に基づく安全性を持つ暗号です。

格子暗号は、①量子耐性があること、②比較的高速な実装が可能であること、③準同型暗号などの高機能暗号との親和性が高いこと、④格子問題は長年研究されており、安全性の理解が進んでいることが利点としてあり、耐量子暗号としての研究や標準化が進んでいます。

格子問題の基礎

格子（Lattice） は、数学的に以下のように定義されます。

$L = { \sum_{i=1}^{n} x_i \mathbf{b}_i : x_i \in \mathbb{Z} }$

ここで、$\mathbf{b}_1, \mathbf{b}_2, \ldots, \mathbf{b}_n$は線形独立なベクトル（基底）です。

格子の直感的な理解

格子を理解するために、身近な例を考えてみます。

2次元の格子の例

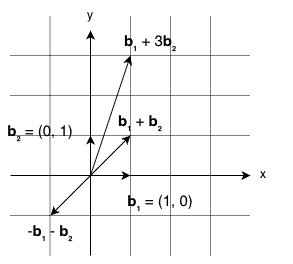
平面上に2つのベクトル $\mathbf{b}_1 = (1, 0)$ と $\mathbf{b}_2 = (0, 1)$ を考えます
この2つのベクトルを「基底」として、整数倍の組み合わせで作られる点の集合が格子です
つまり、$(x_1, x_2)$ という点は、$x_1 \mathbf{b}_1 + x_2 \mathbf{b}_2 = (x_1, x_2)$ として表現されます
これは、座標軸上の整数座標の点（格子点）の集合になります

3次元の格子の例

3つのベクトル $\mathbf{b}_1 = (1, 0, 0)$、$\mathbf{b}_2 = (0, 1, 0)$、$\mathbf{b}_3 = (0, 0, 1)$ を基底とすると
3次元空間内の整数座標の点（立方体の格子）ができます

一般の格子

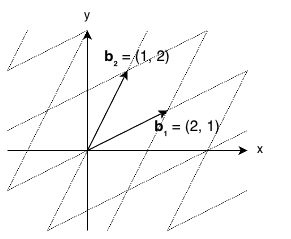
基底ベクトルが必ずしも座標軸に沿っている必要はありません
例えば、$\mathbf{b}_1 = (2, 1)$、$\mathbf{b}_2 = (1, 2)$ のような斜めのベクトルでも格子を作れます
この場合、格子点は斜めに並んだ点の集合になります

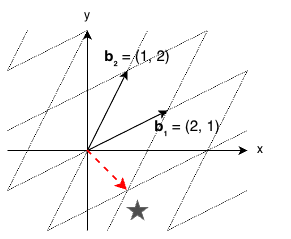
格子暗号では、このような格子の数学的性質（特に「最短ベクトル」や「最近ベクトル」を見つけることの困難性）を暗号の安全性の根拠として利用します。

格子暗号の安全性は、以下の問題の困難性に基づいています。

最短ベクトル問題（SVP） ：格子内の最短非零ベクトルを見つける
最近ベクトル問題（CVP） ：与えられた点に最も近い格子点を見つける（SVPより一般的）

LWE問題（Learning With Errors）

LWE問題（Learning With Errors） は、格子暗号の最も重要な数学的問題です。

LWE問題の定義

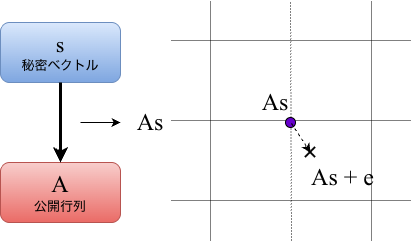
$n$次元のベクトル$\mathbf{a} \in \mathbb{Z}_q^n$と、ノイズ$e \in \mathbb{Z}_q$が与えられたとき、以下の方程式を満たす秘密ベクトル$\mathbf{s} \in \mathbb{Z}_q^n$を見つける問題です。

$$b = \langle \mathbf{a}, \mathbf{s} \rangle + e \pmod{q}$$

ここで、$e$は小さなノイズ（通常、$|e| \ll q$）です。

LWE問題の直感的な理解

LWE問題を身近な例で理解してみます。

簡単な例（$n=2$の場合）

秘密ベクトル：$\mathbf{s} = (3, 7)$（これは秘密にしておく）
公開ベクトル：$\mathbf{a} = (2, 5)$
ノイズ：$e = 1$（小さな値）
法：$q = 17$

このとき、$b = \langle \mathbf{a}, \mathbf{s} \rangle + e = (2 \times 3 + 5 \times 7) + 1 = 6 + 35 + 1 = 42 \equiv 8 \pmod{17}$

攻撃者の視点

攻撃者は $\mathbf{a} = (2, 5)$ と $b = 8$ を知っています
しかし、ノイズ $e = 1$ の存在により、正確な内積値は分かりません
攻撃者は $\mathbf{s} = (3, 7)$ を見つけようとしますが、ノイズがあるため困難です

なぜ攻撃が困難なのか

ノイズの存在 ：正確な方程式ではなく、ノイズが加わった方程式を解く必要があります
多次元性 ：$n$が大きくなるほど、解の候補が指数的に増加します
格子問題との関連 ：この問題は格子の「CVP（最近ベクトル問題）」に帰着できます

ちなみにこの問題は、以下のような連立1次"近似"方程式（連立線形近似方程式）の解を求めるような問題と一致します。誤差は一定以内とします。

\begin{equation}
\left\{ \,
    \begin{aligned}
    & 2 s_1 + 5 s_2 \fallingdotseq 8 \pmod {17} \\
    &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \  \vdots \\
    & 3s_1 + s_2 \fallingdotseq 1 \pmod {17}
    \end{aligned}
\right.
\end{equation}

誤差がなく、近似でなければGaussの消去法で効率的に解を求められますが、誤差が存在することにより解を求めるのが困難になります。また誤差が大きいほど解を求めることが難しくなります。

LWEの困難性とそれによる安全性

LWE問題は、格子問題の一種である最短独立ベクトル問題（SIVP） に帰着できることが知られており、量子コンピュータでも効率的に解く方法は見つかっていません。

現在の最良のアルゴリズムでも、$n$次元のLWE問題を解くには指数時間が必要
量子コンピュータのShorのアルゴリズムは、素因数分解や離散対数問題には適用できるが、LWE問題には適用できない
格子問題は長年研究されており、数学的に深く理解されている

Ring-LWE

Ring-LWE は、LWEを多項式環上に拡張した問題です。通常のLWEが$n$次元のベクトル同士の内積を計算するのに対し、Ring-LWEは$n-1$次以下の多項式同士の掛け算を計算します。

多項式環$R_q = \mathbb{Z}_q[X]/(X^n + 1)$において、$a \in R_q$とノイズ$e \in R_q$が与えられたとき、以下の方程式を満たす秘密多項式$s \in R_q$を見つける問題です。

$$b = a \cdot s + e \pmod{q}$$

ここで、$a$は公開多項式、$s$は秘密多項式、$e$は小さい係数を持つノイズ多項式です。多項式環 $R_q = \mathbb{Z}_q[X]/(X^n + 1)$ は、$X^n \equiv -1 \pmod{q}$ という関係式を持ち、高次の項（$X^n$以上）が低次の項に折り返されるため、多項式の次数は常に$n-1$次以下に保たれます。

Ring-LWEの主な利点は、鍵サイズの大幅な削減と計算効率です。Ring-LWEも通常のLWEと同様に格子問題の困難性に基づいていますが、多項式環の構造を利用するため、通常のLWEよりもやや弱い安全性保証となる可能性が理論的に指摘されています。

Module-LWE

Module-LWE は、Ring-LWEをさらに拡張したもので、複数の多項式をベクトルとして扱いま
す。Ring-LWEとベクトルLWEの中間的な性質を持ちます。

Ring-LWE：多項式1つ（鍵サイズは小さいが、安全性パラメータの柔軟性が低い）
Module-LWE：多項式のベクトル（鍵サイズと安全性のバランスが良い）
通常のLWE：完全なベクトル（鍵サイズが大きいが、安全性パラメータの柔軟性が高い）

ML-KEMやML-DSAなどの現代的な格子暗号は、このバランスの良いModule-LWEを採用しています。

格子暗号の応用例

ML-KEM（CRYSTALS-Kyber）

ML-KEM（CRYSTALS-Kyber）は、Lindner-Piekart公開鍵方式をModule-LWE問題に基づく鍵カプセル化メカニズム（Key Encapsulation Mechanism, KEM）に拡張したものです。KEMは、メッセージを直接暗号化するのではなく、送信者と受信者の間で共有秘密鍵を安全に確立するための仕組みです。この共有秘密鍵を使って、AESなどの共通鍵暗号でデータを暗号化します。

ML-KEMは、NISTのPQC標準化プロジェクトで最初に選定されたアルゴリズムの一つで、TLS通信や鍵交換プロトコルでの利用が想定されています。

格子暗号の中でも実装が高速で、TLS通信などリアルタイム性が求められる用途に適しています。公開鍵は約800バイト〜1.6KB、暗号文は約768バイト〜1.6KBと、RSA暗号と比較してやや大きいですが実用的なサイズとなっています。安全性としては、Fujisaki-Okamoto変換により、選択暗号文攻撃（CCA2）への耐性を持ちます。

アルゴリズムの構成

ML-KEMは、Module-LWE問題に基づいており、セキュリティレベルに応じて3つのパラメータセットがあります。

ML-KEM-512 ：AES-128相当のセキュリティ
ML-KEM-768 ：AES-192相当のセキュリティ
ML-KEM-1024 ：AES-256相当のセキュリティ

鍵生成（KeyGen）

ランダムシード$\rho, \sigma$を生成
$\rho$から公開行列$\mathbf{A} \in R_q^{k \times k}$を決定論的に生成（$k$はパラメータセットにより2, 3, 4）
$\sigma$から秘密ベクトル$\mathbf{s} \in R_q^k$とエラーベクトル$\mathbf{e} \in R_q^k$を生成（係数は小さい値）
$\mathbf{t} = \mathbf{A}\mathbf{s} + \mathbf{e} \pmod{q}$を計算
公開鍵：$(\mathbf{t}, \rho)$、秘密鍵：$\mathbf{s}$

カプセル化（Encaps）
送信者が受信者の公開鍵を使って共有秘密鍵を生成する処理です。以下では、計算の複雑性を取り除き、高速化するためのNTT（Number-Theoretic Transform）と呼ばれる処理などの詳細は省略しています。

ランダムな値$m \in {0,1}^{256}$を生成
ハッシュ関数（SHA-3）を使って、共有秘密鍵$K$と暗号化用のランダム値$r$を導出
$r$から$\mathbf{y}, \mathbf{e_1}, e_2 \in R_q$を生成
$\mathbf{u} = \mathbf{A}^T\mathbf{y} + \mathbf{e_1} \pmod{q}$を計算
$v = \mathbf{t}^T\mathbf{y} + e_2 + \text{Encode}(m) \pmod{q}$を計算
暗号文$c = (\mathbf{u}, v)$と共有秘密鍵$K$を出力

脱カプセル化（Decaps）
受信者が自分の秘密鍵を使って、暗号文から共有秘密鍵を復元する処理です。以下では、計算の複雑性を取り除き、高速化するためのNTT（Number-Theoretic Transform）と呼ばれる処理などの詳細は省略しています。

$m' = \text{Decode}(v - \mathbf{s}^T\mathbf{u} \pmod{q})$により$m$を復元
ハッシュ関数（SHA-3）を使って$m'$から共有秘密鍵$K'$を導出
$m'$を使って暗号文を再計算し、受信した暗号文と一致することを確認（Fujisaki-Okamoto変換による安全性強化）
一致すれば$K'$を、一致しなければ失敗値を出力

ML-KEMの応用事例

純粋なML-KEMでは、実世界のネットワーク環境に対応しにくいため、それに対応するためのプロトコルなども考えられています。

Signal | The ML-KEM Braid Protocol

またこれらをもとに、Signalでは、耐量子暗号技術をもとにしたメッセージングの各種通信を実現するプロトコル（PQXDH：Post-Quantum Extended Diffie-Hellman、SPQR：Sparse Post-Quantum Ratchet）などを設計、実装しており、実世界での活用も進んでいます。

NTRU暗号

NTRU暗号は、多項式環上での計算に基づく格子暗号で、1996年に提案された初期の格子暗号アルゴリズムの一つです。多項式環$R = \mathbb{Z}[X]/(X^N - 1)$上での演算を使用し、シンプルな構造ながら高い効率性を持ちます。
特徴として、多項式演算により効率的な実装が可能なため高速です。また、1996年の提案以来、安全性評価が継続されており、長期間研究されていることも挙げられます。

7.5 多変数多項式暗号（Multivariate Cryptography）

多変数多項式問題

多変数多項式暗号 は、多変数多項式方程式の解を求める困難性（NP困難）に基づく暗号です。

多変数二次方程式問題（MQ問題）

$n$個の変数$x_1, x_2, \ldots, x_n$に関する$m$個の二次方程式

$$f_i(x_1, x_2, \ldots, x_n) = 0 \quad (i = 1, 2, \ldots, m)$$

の解を見つける問題は、一般にNP困難であることが知られています。

多変数暗号の仕組み

多変数暗号は主にディジタル署名に使用されます。核となるアイデアは、「解きやすい多項式」を「解きにくく見せる」ことです。

トラップドア構造

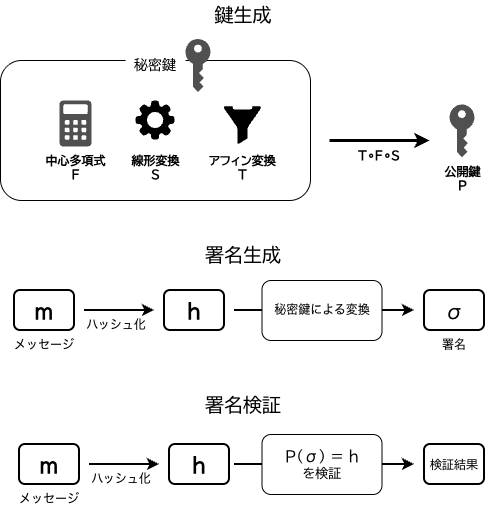
多変数暗号では、以下の3つの要素を組み合わせます：

線形変換$S$ ：$S: \mathbb{F}^n \rightarrow \mathbb{F}^n$（可逆なアフィン変換）
中心多項式$F$ ：$F: \mathbb{F}^n \rightarrow \mathbb{F}^m$（解きやすい特殊な構造を持つ多変数多項式）
アフィン変換$T$ ：$T: \mathbb{F}^m \rightarrow \mathbb{F}^m$（可逆なアフィン変換）

鍵生成

解きやすい中心多項式$F$を選択（これがトラップドアの核心）
ランダムな可逆変換$S$と$T$を生成
公開鍵：$P = T \circ F \circ S$（合成関数として計算された多項式）
秘密鍵：$(S, F, T)$

署名生成

メッセージ$m$の署名を生成する手順の概要は以下になります。

$h = H(m)$：メッセージをハッシュ化
$y = T^{-1}(h)$：$T$の逆変換を適用
$F(x) = y$の解$x$を見つける（$F$は解きやすい構造なので効率的に計算可能）
$\sigma = S^{-1}(x)$：$S$の逆変換を適用
署名：$\sigma$

秘密鍵保持者は$S, F, T$を知っているため、$T^{-1}$と$S^{-1}$を計算でき、さらに中心多項式$F$の特殊な構造により$F(x) = y$を効率的に解けます。

署名検証

署名$\sigma$の検証

$h = H(m)$：メッセージを同じハッシュ関数で処理
$P(\sigma) = h$を確認
一致すれば署名を受理

多変数多項式暗号の特徴

攻撃者は公開鍵$P$しか知らず、$P(\sigma) = h$を満たす$\sigma$を見つける必要がありますが、これは一般的なMQ問題を解くことに相当し、NP困難となります。$F$の特殊な構造は$S$と$T$により完全に隠蔽されており、攻撃者は容易に引き出すことができません。

利点と欠点

多変数多項式暗号の利点として、MQ問題は量子コンピュータでも効率的に解けないため、耐量子暗号となります。署名生成および検証は高速に実行可能です。秘密鍵や署名サイズが比較的小さいことも良い点として挙げられます。

一方、公開鍵$P$は$m$個の$n$変数二次多項式で構成され、サイズが大きくなります（数十KB〜数百KB）。一部の多変数暗号（HFE、Sflashなど）で解読法が発見されており、各方式で慎重な安全性評価が必要である点や、安全な中心多項式$F$の設計が難しいため、安全性の保証に対する難しさも存在します。

代表的な多変数暗号

UOV署名（Unbalanced Oil and Vinegar）

UOV署名は、変数をOil変数とVinegar変数の2種類に分離した構造を持つ多変数署名方式です。特徴として、長年の研究により安全性が評価されており、NISTの標準化では最終候補には選ばれませんでしたが、有力な候補の一つだった暗号技術です。選ばれなかった理由でもありますが、公開鍵サイズが大きいことが課題となっています。

仕組み

$n$個の変数を、$o$個のOil変数と$v$個のVinegar変数に分割（$n = o + v$、$v > o$）
中心多項式$F$は、Oil変数同士の積の項を含まない特殊な構造を持ちます
この構造により、Vinegar変数を固定すると線形方程式となり、効率的に解けます

Rainbow署名

Rainbow署名は、UOVを多層化した構造を持ち、より効率的な実装を実現していました。ただし、2022年に新しい攻撃法が発見され、NISTの標準化候補から除外されました。

7.6 同種写像暗号（Isogeny-Based Cryptography）

同種写像問題

同種写像（Isogeny） は、楕円曲線間の有理写像で、有限群の準同型写像を誘導するものです。

誘導とは、ある数学的構造（今回では同種写像）から別の数学的構造（今回では群準同型）が自然に出てくることを言います。同種写像は楕円曲線の持つ群のルールを壊さないため、自然に「準同型性」が得られます。

楕円曲線$E_1$から$E_2$への同種写像$\phi$は、以下の条件を満たす有理写像（変換ルールが分数で表現される写像）として定義されます。

$$\phi(\mathcal{O}_{E_1}) = \mathcal{O}_{E_2}\ (\phiは有限群の準同型写像を誘導)$$

同種写像問題 は、2つの楕円曲線$E_1$と$E_2$が与えられたとき、それらを結ぶ同種写像を見つける問題です。この問題は、量子コンピュータでも効率的に解く方法は見つかっていないため、これをもとにする暗号は耐量子暗号となります。

SIDH（Supersingular Isogeny Diffie-Hellman）

SIDHは、同種写像問題に基づく鍵交換プロトコルとして2011年に提案され、小さな鍵サイズと量子耐性を兼ね備えた有望な方式として注目されました。NISTのPQC標準化プロジェクトにおいて、SIKE（Supersingular Isogeny Key Encapsulation）として候補に選ばれるなど、実用化が期待されていました。

SIDHの仕組み

SIDHは、Diffie-Hellman鍵交換を楕円曲線の同種写像を使って実現したプロトコルです。AliceとBobがそれぞれ秘密の同種写像を選択し、公開情報を交換することで共通秘密鍵を生成します。

SIDHの脆弱性の発覚

2022年7月から8月にかけて、Wouter CastryckとThomas Decruは、SIDHおよびSIKEに対する攻撃手法を発表しました。

この攻撃手法は、量子コンピュータではなく現代のコンピュータで実行可能で、NISTのPQC候補であったSIKEp434が、単一コアのPCを用いて約1時間で解読できることが判明しています。

攻撃者は公開情報に含まれる補助点を利用し、楕円曲線の性質をより広い世界に写して（数学的に言えば「構造を持ち上げて」）解析することで、秘密鍵の計算につながる情報を効率的に抽出することに成功しました。この攻撃は、SIDHの根本的な設計思想に対する攻撃であり、パラメータを大きくしたりするだけでは対処できません。

この攻撃手法が発見により、SIDHは、NISTのPQC標準化候補から除外されました。同様に補助点を公開するSIDH系の方式は安全でないことが判明しています。ただし、CSIDH、SQISignなど、補助点を使用しない他の同種写像暗号方式は、この攻撃の直接的な影響を受けておらず、耐量子暗号として活用される可能性があります。

暗号技術への教訓

SIDHに対する攻撃手法の発見は、比較的新しい暗号技術に対する安全性評価の難しさと、安全性の確保に対する教訓を与えてくれています。

SIDHは10年以上研究されてきましたが、暗号方式そのものに根本的な脆弱性が見つかりました。新しい暗号方式には、時間をかけた慎重な安全性評価が必要となることを示しています。こうした特定の暗号方式に対する脆弱性が発見される可能性は、他の暗号手法にも言えることであり、NISTが複数の異なる数学的基盤（格子、符号、ハッシュ、多変数、同種写像）に基づくアルゴリズムを標準化候補としている理由の一つになります。一つの方式に依存することは、有用な攻撃手法が見つかった場合に移行先となる暗号方式が準備できない可能性もありリスクとなります。

SIDHは効率性のために補助点を公開していましたが、これが攻撃の突破口となったことから、プロトコル設計においては、公開する情報は必要最小限にすることも重要です。

7.7 符号ベース暗号（Code-Based Cryptography）

符号ベース暗号は誤り訂正符号をもとにしているため、まずは誤り訂正符号について簡単に説明したうえで、符号ベース暗号の概略を説明します。

誤り訂正符号の基礎

誤り訂正符号 は、データ伝送時の誤りを検出・訂正するための符号化技術です。

たとえば、AliceがBobに対して、3ビットの値を送信するとします。

しかし何らかの理由で一部が誤った値をBobが受信する可能性があります。

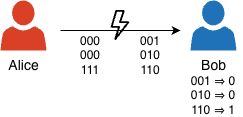
これに対し、単純な誤り訂正符号では、多数決をもって対処します。

これまで3ビットの値は3ビットのまま送信していましたが、1ビットごとに3ビットまで増やして値を送信します。こうすると、3ビットのうち1ビットまでであれば、誤った値となっても「多数決」を取ることで正しい値に戻すことができます。

線形符号

線形符号は誤り訂正符号の一種で、以降で説明する符号ベース暗号であるMcEliece暗号で利用されています。

$n$次元ベクトル空間$\mathbb{F}_2^n$の$k$次元部分空間$C$を線形符号と呼びます。$C$は $k\times n$の生成行列$G \in \mathbb{F}_2^{k \times n}$によって

\begin{align}
C = \{ \mathbf{m}G : \mathbf{m} \in \mathbb{F}_2^k \}
\end{align}

と表現されます。

シンドローム復号

受信したベクトル$\mathbf{y}$から元の符号語$\mathbf{c}$を復元するには、パリティ検査行列$H$を使用してシンドローム$\mathbf{s} = H\mathbf{y}^\top$を計算し、誤りパターンを特定します。

McEliece暗号

McEliece暗号 は、1978年にRobert McElieceによって提案された、誤り訂正符号の復号困難性に基づく公開鍵暗号です。

鍵生成

Goppa符号（効率的な復号アルゴリズムを持つ線形符号）の生成行列$G \in \mathbb{F}_2^{k \times n}$を選択
ランダムな可逆行列$S \in \mathbb{F}_2^{k \times k}$を生成
ランダムな置換行列$P \in \mathbb{F}_2^{n \times n}$を生成
公開鍵：$\hat{G} = SGP$
秘密鍵：$(S, G, P)$および復号能力$t$

暗号化

メッセージ$\mathbf{m} \in \mathbb{F}_2^k$の暗号化

$\mathbf{c} = \mathbf{m}\hat{G}$を計算
ランダムな誤りベクトル$\mathbf{e} \in \mathbb{F}_2^n$を生成（ハミング重み$\text{wt}(\mathbf{e}) \leq t$）
暗号文：$\mathbf{y} = \mathbf{c} + \mathbf{e}$

ハミング重み：ベクトルの中で1である要素の個数を指します。$\text{wt}(\mathbf{e}) \leq t$は、最大$t$個のビットを反転させることを意味します。

復号

暗号文$\mathbf{y}$の復号

$\mathbf{y}' = \mathbf{y}P^{-1}$を計算（置換を戻す）
Goppa符号の復号アルゴリズムを適用
- $\mathbf{y}' = \mathbf{m}SG + \mathbf{e}P^{-1}$の形になっている
- Goppa符号は最大$t$個の誤りを訂正できるため、$\mathbf{e}P^{-1}$を除去
- 符号語$\mathbf{c}' = \mathbf{m}SG$を復元
$\mathbf{c}'$から$\mathbf{m}S$を抽出（生成行列$G$が系統形式の場合、メッセージ部分が直接含まれる）
$\mathbf{m} = (\mathbf{m}S)S^{-1}$により元のメッセージを復元

秘密鍵保持者は、$P^{-1}$で置換を戻し、Goppa符号の特殊な構造と効率的な復号アルゴリズム（Pattersonアルゴリズムなど）を使って誤りを訂正できます。その後、$S$を使って元のメッセージを復元します。

符号ベース暗号の特徴

一般的な線形符号に対して、誤りを含む受信語から元の符号語を復号する問題（符号語復号問題）はNP困難であり、それをベースとした符号ベース暗号では耐量子暗号となります。

符号ベース暗号の利点として、1978年の提案以来40年以上にわたって根本的な解読法は発見されておらず、安全性が高い暗号と考えられています。また、暗号化処理が行列とベクトルの積とビット演算のみで実装できるため、高速に処理できる点が挙げられます。

欠点として、公開鍵$\hat{G}$は$k \times n$の行列で、サイズが非常に大きい（数十KB〜数百KB）ことや、暗号文のサイズが元のメッセージの2倍程度になる点が挙げられます。さらに、Goppa符号の復号アルゴリズムは複雑で、実装が難しいとされています。

現代的な符号ベース暗号

Classic McEliece

Classic McElieceは、元のMcEliece暗号を改良したもので、より効率的な実装と標準化への適合性を向上させています。ただし、公開鍵が非常に大きくなるなどの欠点があり、標準化等には至っていません。

HQC（Hamming Quasi-Cyclic）

HQCは、準巡回符号（Quasi-Cyclic codes）を使用した鍵カプセル化メカニズム（KEM）で、NISTのPQC標準化プロジェクトで2025年3月に標準化が決定しました。符号ベース暗号の中でも、実用的な鍵サイズと効率性のバランスを実現しています。

核となる仕組み

HQCは、McEliece暗号と同様に誤り訂正符号の復号困難性に基づいていますが、準巡回構造を利用することで鍵サイズを大幅に削減しています。準巡回符号は、符号語が巡回シフト（回転）によって生成される特殊な構造を持つため、少ない情報で符号全体を表現できます。

特徴

実用的な鍵サイズ：公開鍵は約2〜4KB程度で、格子暗号（ML-KEM）と同程度のサイズ
高速な演算：準巡回構造により、効率的な実装が可能
符号ベースの安全性：40年以上の研究実績を持つ符号理論に基づく
量子耐性：符号語復号問題は量子コンピュータでも効率的に解けない
多様性の確保：格子暗号とは異なる数学的基盤を提供

NIST標準化での位置づけ

HQCは、ML-KEM（格子ベース）に加えて、符号ベース暗号による鍵交換の選択肢として標準化されます。格子暗号に脆弱性が発見された場合にも、異なる数学的基盤に基づく多様性を確保する目的で重要な役割を果たします。Classic McElieceと比較して、より実用的な鍵サイズを実現している点が評価されました。

7.8 ハッシュベース署名（Hash-Based Signatures）

ハッシュベース署名の原理

ハッシュベース署名 は、暗号学的ハッシュ関数のみを使用して構成される署名方式です。その安全性は、ハッシュ関数の衝突耐性と原像困難性に基づいています。

ワンタイム署名（OTS）

ワンタイム署名 は、各秘密鍵を一度だけ使用する署名方式です。同じ秘密鍵を複数回使うことができません。

Lamport署名

Lamport署名は、1979年にLeslie Lamportによって提案された、最も基本的なワンタイム署名方式です。暗号学的ハッシュ関数の一方向性のみに依存するシンプルな構造を持ちます。

メッセージの各ビット（0または1）に対応する秘密値をあらかじめ用意しておき、署名時にはメッセージのビット値に応じた秘密値を公開します。検証者は、公開された値をハッシュ化して公開鍵と照合することで署名を検証します。

ワンタイムである理由は、同じ秘密鍵で2つの異なるメッセージに署名すると、あるビット位置で0と1の両方に対応する秘密値が漏洩する可能性があるためです。これにより、攻撃者は任意のメッセージを偽造できるようになるため、各秘密鍵は一度しか使用できません。

ハッシュ関数のみを使用しているため、構造がシンプルですが、256ビットのメッセージに対して、公開鍵は約16KB、署名は約8KBと非常に大きく、ワンタイム制約により、単独での実用性は限定的となります。

Winternitz署名（WOTS）

Winternitz署名（Winternitz One-time signature, WOTS）は、Lamport署名を改良したワンタイム署名方式で、署名サイズを大幅に削減します。より実用的なハッシュベース署名（XMSSやSLH-DSAなど）の基礎として利用されています。

Lamport署名は、メッセージのハッシュ値を「1ビットごと」に処理しますが、Winternitz署名ではハッシュ値を複数ビットまとめてチャンクとして扱います。さらに、ハッシュ関数の連鎖適用を利用して、署名サイズを削減しながらも安全性を保ちます。ただし、署名サイズの削減と引き換えに、署名生成・検証の計算量が増加するトレードオフが存在します。

複数回署名

ワンタイム署名と異なり、秘密鍵を複数回利用できます。ハッシュベース署名では、主に2つのアプローチがあります。状態を持つ方式（Merkle署名系）とステートレス方式（SLH-DSA）です。

Merkle署名

Merkle署名は、1979年にRalph Merkleによって提案された、複数のワンタイム署名を組み合わせて複数回署名を実現する方式です。

$2^h$個のワンタイム署名鍵ペアを事前に生成し、それらをMerkle木（ハッシュ木）で管理します。このMerkle木の「ルートハッシュ」が公開鍵となります。これにより、公開鍵のサイズを削減できます。署名時には、未使用のワンタイム署名鍵を1つ選択して署名を生成し、Merkle木の認証パス（その鍵がルートハッシュに含まれることの証明）を添付します。検証者は、ワンタイム署名を検証し、認証パスをたどってルートハッシュと一致することを確認します。

各ワンタイム署名鍵は一度しか使えないため、どの鍵を使用したかを記録する状態管理が必須です。状態の喪失や誤った管理は、秘密鍵の再利用による安全性の崩壊につながります。
また、$2^h$個のワンタイム署名鍵を用意するため、最大$2^h$回の署名しかできません（$h = 20$なら約100万回）。

XMSS（eXtended Merkle Signature Scheme）

XMSS（eXtended Merkle Signature Scheme）は、Winternitz署名（WOTS）を改良した WOTS⁺ を基盤にし、Merkle Tree と組み合わせることで複数回の署名を可能にしたハッシュベース署名方式で、RFC 8391 により標準化されています。量子コンピュータに対しても安全で、厳密なセキュリティ証明を持つ点が特徴です。

一方で、状態管理（使用済み葉の追跡）が必須で、実装には注意が必要です。ハッシュベース署名方式の中では効率と安全性のバランスが良く、実用的に利用できる設計となっています。

LMS（Leighton-Micali Hash-Based Signature）

LMS は Merkle木を利用したハッシュベース署名方式で、RFC 8554 により標準化されています。XMSS と同様に状態管理が必要な方式ですが、実装が比較的容易です。このため、リソース制約のある組み込み機器やファームウェア署名など、軽量な実装が求められる用途に適しています。

SLH-DSA（SPHINCS+）

SLH-DSAは、NISTのPQC標準化プロジェクトで2022年7月に選定され、2024年8月にFIPS 205として正式標準化されたハッシュベース署名方式です。
特徴として、他のハッシュベース署名（XMSS、LMS）と異なり、SLH-DSAは状態管理が不要です。署名回数の制限もなく、従来の署名方式（RSA、ECDSAなど）と同じように使用できます。

多層のハッシュ木構造とランダム化技術を組み合わせることで、状態管理なしでも安全性を確保しています。ただし、署名サイズと署名生成時間は、状態を持つ方式と比較して、一般的に大きく、遅くなります。

NIST標準化での位置づけ

ML-DSA（格子暗号ベース）とともにディジタル署名の標準として選定されました。SLH-DSAは、格子暗号に脆弱性が発見された場合でも利用可能であり、そうした意味でも重要です。

7.9 実世界の動向

暗号解読可能な量子コンピュータ実現より速く、耐量子暗号への移行を実現する必要があるため、すでに現実でも導入が進んでいます。それらの一部について紹介します。

耐量子暗号の各社の導入

Google

Googleは2016年から、TLS 1.3にPQCアルゴリズム（ML-KEM）を組み込んだ実験を開始しました。ChromeブラウザとGoogleサーバ間で、従来の楕円曲線暗号とPQCアルゴリズムを併用するハイブリッド鍵交換 を実装しています。2024年5月には、PC向けのChromeブラウザで、TLS 1.3とQUIC用のML-KEMをデフォルトで有効化しています。

また、OpenSSLをフォークした、BoringSSLにて、ML-KEM768（Kyber-768）を実装し、Chromeブラウザ等で利用しています。

Apple

メッセージングアプリの iMessage に耐量子暗号プロトコルであるPQ3を導入しています。

Cloudflareの実験

Cloudflareも同様に、PQCアルゴリズムをTLSに統合する実験を行っています。これにより、量子コンピュータが実現した場合でも、過去の通信が解読されないことを保証します。

AWS

AWSも耐量子暗号の導入に関して、2024年に移行計画を発表しています。

AWS Key Management Service（KMS）、AWS Certificate Manager（ACM）、AWS Secrets Manager でPQCハイブリット鍵交換をサポートしています。

Microsoft

Microsoftは、Microsoft Quantum Safe Programとして、2033年までの耐量子暗号への完全移行を目指しています。また、2024年にはWindows 11のInsider Preview版でPQC機能の公開をしました。Azure、Windows、Officeの暗号基盤であるSymCryptライブラリに、NIST標準アルゴリズム（ML-KEM, ML-DSA）を統合中です。

Meta（Facebook）

2024年5月にブログで耐量子暗号移行への取り組みを公開しています。社内サービス間の通信（TLS）をKyberを用いたハイブリット暗号で実装、それを導入しています。

OSSの対応

OpenSSL

バージョン3.2移行で実験的にサポートを開始しています。OQSプロジェクトが提供するプロバイダを介して、PQCアルゴリズムを利用可能です。

電子署名への応用

政府・金融機関での導入

各国の政府や金融機関は、長期的なデータ保護のためにPQCアルゴリズムの導入を検討しています。特に、機密性が長期間必要となるデータ（医療記録、法的文書など）の保護に重要です。特に、医療機器などは利用期間が非常に長く、より早期での対応が求められます。

暗号資産への応用

ビットコイン・イーサリアム

主要な暗号資産プロジェクトは、PQCアルゴリズムへの移行を検討しています。特に、長期的な価値保存を目的とする暗号資産では、量子耐性が重要です。

新しい暗号資産

一部のプロジェクト（QRL、Algorandなど）では、最初からPQCアルゴリズムを使用した暗号資産を開発しています。

各国の動き

世界各国で耐量子暗号への移行の動きは加速しています。とくに去年にはNISTで一部の耐量子暗号技術についての標準化が実現され、実際の移行計画の策定やロードマップが示されるようになってきています。

特に動きが速いのはアメリカ、オーストラリアです。アメリカはすでに耐量子暗号に対する移行が法制化されており、現実的な耐量子暗号への移行が進行しています。オーストラリアでは、2030年末までの耐量子暗号への移行完了という野心的な目標を掲げています。

H.R.7535 - Quantum Computing Cybersecurity Preparedness Act
ASD | Planning for post-quantum cryptography

その他の先進国・地域でも2035年前後を目標に耐量子暗号への移行完了を目標としているところが多いです。政府各国の動きに合わせて、政府機関以外のサービスやシステムに関しても移行が進むと予想されます。

日本でもつい先日の2025年11月20日に国家サイバー統括室（NCO）から、2035年までの政府機関での耐量子暗号への移行計画の発表がありました。

政府機関等における耐量子計算機暗号（PQC）への移行について（中間とりまとめ）

実装の課題

実世界でも導入が進んでいる耐量子暗号ですが、実装においてはまだ課題も存在しています。大きな課題を以下に記載します。

性能オーバーヘッド

PQCアルゴリズムは、従来の暗号と比較して計算コストが高い場合があります。特に、モバイルデバイスやIoT機器での実装には注意が必要です。これまでの暗号技術より複雑な処理が必要なアルゴリズムも多く、これまで以上にハードウェアへの最適化等が必要になる可能性があります。
また、多くのPQCアルゴリズムは、従来の暗号と比較して鍵サイズや署名サイズが大きくなります。これにより、ネットワーク帯域やストレージ容量への影響を考慮する必要があります。

標準化の遅れ

PQCアルゴリズムの標準化は一部完了していますが、利用される暗号技術に多様性を持たせるための複数の理論的基盤を基にしたアルゴリズムの完全な標準化までにはまだ時間がかかります。さらに、標準化されたアルゴリズムでも、長期的な安全性の評価は継続的に行う必要があります。

対応ライブラリやサービスの不足

PQCアルゴリズムをサポート、採用しているライブラリやサービスはまだ多いとは言えず、場合によっては新たなライブラリやサービスへの移行などの検討も必要になる可能性があります。

システムや機器の移行作業の遅延

特に医療機関や各自治体などにおける、入れ替えに多額のコストがかかる古いシステムや機器では、簡単に対応ができない場合もあります。

7.10 まとめと今後の展望

本記事の要点

本記事では、量子コンピュータがもたらす暗号技術への脅威と、それに対抗するための耐量子暗号について詳しく解説しました。

主要な従来の暗号への脅威

Shorのアルゴリズム ：RSA暗号や楕円曲線暗号を解読
Groverのアルゴリズム ：対称鍵暗号の安全性を鍵長に対して半減

耐量子暗号の種類

格子暗号 ：LWE問題に基づく、効率的で高機能
多変数多項式暗号 ：MQ問題に基づく、高速な署名
同種写像暗号 ：小さな鍵サイズ、楕円曲線ベース
符号ベース暗号 ：高い安全性、大きな鍵サイズ
ハッシュベース署名 ：高い安全性、大きな署名サイズ

今後の暗号技術

標準化の進展

NISTのPQC標準化プロジェクトの完了により、業界標準としてのPQCアルゴリズムが確立され、実装と展開が加速されることが期待されます。

各ITサービスの導入計画や実現

一部サービスやアプリケーションにおいては、すでに実験的なPQCの導入がスタートしており、これは徐々に多くのサービスやアプリケーションへと広がっていくことが想定されます。

開発者への影響

暗号技術を使用する開発者は、以下の点を考慮する必要があります。

PQCアルゴリズムの特性理解
性能要件の見直し
鍵管理システムの更新
セキュリティプロトコルの改訂
耐量子暗号をサポートする利用ツールやライブラリへの移行、アップデート
インフラやデータの移行計画の策定、実施

全体のまとめ

本連載では、暗号技術の基礎から最新の高機能暗号、そして耐量子暗号まで、包括的に理解してきました。

学んだ内容

暗号技術の基礎 ：各暗号技術の概要、安全性モデル、計算量的困難性
共通鍵暗号 ：ブロック暗号、ストリーム暗号、DES、AES、暗号モード
ハッシュ関数とMAC ：ハッシュ関数、完全性、認証の仕組み
公開鍵暗号 ：Diffie-Hellman鍵共有、RSA暗号、楕円曲線暗号
高機能暗号 ：IDベース暗号、属性ベース暗号、検索可能暗号、匿名署名
耐量子暗号 ：量子コンピュータによる脅威への対応

実世界との関連

各記事で取り上げた暗号技術は、TLS、VPN、暗号資産、電子署名など、現代のディジタル社会を支える重要な技術として実際に使用されています。

今回紹介した以外の暗号技術

暗号技術は急速に発展している分野です。本連載で学んだ基礎知識以外にも、以下のような分野の暗号に関連する技術が発展しています。

量子暗号 ：量子力学を利用した暗号技術
マルチパーティ計算 ：プライバシー保護型の分散計算
ゼロ知識証明 ：情報を開示せずに証明を行う技術
ブロックチェーン暗号 ：分散システムにおける暗号技術

さいごに

今回は、ディジタルインフラの基盤の一つとなっている暗号技術の現在の状況を、広く使われている共通鍵暗号や公開鍵暗号、ハッシュ関数などの技術から、最新の研究段階や導入が始まった高機能暗号や耐量子暗号の技術まで幅広く見ていきました。

実際の詳細な数学的背景や安全な暗号実装のための技術は、今回の記事では多くは触れませんでした。そのため、暗号自体を安全に実装するという視点ではまだまだ不足する知識が多く存在します。しかしながら、今後、日々進化する各種技術による脅威に対して、どのように開発するシステムや利用するサービスでの安全性を担保できるよう暗号技術を選択していくべきかの基礎となる知識を得ることができました。

今回の連載記事は、暗号技術の触り程度であり、暗号技術はまだまだ奥深いものです。興味がある方はぜひ、各種文献やライブラリ実装、また今回は紹介できなかった技術などに触れていただければと思います。

第7回 耐量子暗号とこれからの暗号技術【連載：暗号技術の基礎を学ぶ】

目次

7.1 量子コンピュータと従来の暗号への脅威

量子コンピュータとは

Shorのアルゴリズムによる脅威

RSA暗号への影響

楕円曲線暗号への影響

Groverのアルゴリズムによる脅威

対称鍵暗号への影響

ハッシュ関数への影響

量子コンピュータの現状

7.2 NIST PQC標準化プロジェクト

標準化の背景

標準化プロセスの流れ

標準化の現状

7.3 耐量子暗号への移行の課題

CRYPTREC暗号技術ガイドライン（耐量子計算機暗号）2024年度版

移行期間が必要な理由

技術的な準備期間

段階的移行の必要性

1. プライオリティ設定

2. クリプトグラフィック・アジリティの確保

3. 既存暗号方式とのハイブリッド構成の利用

耐量子暗号への移行期間の全体像

ハーベスト攻撃の脅威

耐量子暗号の候補となる暗号技術

7.4 格子暗号（Lattice-Based Cryptography）

格子問題の基礎

格子の直感的な理解

LWE問題（Learning With Errors）

LWE問題の定義

LWE問題の直感的な理解

LWEの困難性とそれによる安全性

Ring-LWE

Module-LWE

格子暗号の応用例

ML-KEM（CRYSTALS-Kyber）

アルゴリズムの構成

ML-KEMの応用事例

NTRU暗号

7.5 多変数多項式暗号（Multivariate Cryptography）

多変数多項式問題

多変数二次方程式問題（MQ問題）

多変数暗号の仕組み

トラップドア構造

鍵生成

署名生成

署名検証

多変数多項式暗号の特徴

利点と欠点

代表的な多変数暗号

UOV署名（Unbalanced Oil and Vinegar）

仕組み

Rainbow署名

7.6 同種写像暗号（Isogeny-Based Cryptography）

同種写像問題

SIDH（Supersingular Isogeny Diffie-Hellman）

SIDHの仕組み

SIDHの脆弱性の発覚

暗号技術への教訓

7.7 符号ベース暗号（Code-Based Cryptography）

誤り訂正符号の基礎

線形符号

シンドローム復号

McEliece暗号

鍵生成

暗号化

復号

符号ベース暗号の特徴

現代的な符号ベース暗号

Classic McEliece

HQC（Hamming Quasi-Cyclic）

核となる仕組み

特徴

NIST標準化での位置づけ

7.8 ハッシュベース署名（Hash-Based Signatures）

ハッシュベース署名の原理

ワンタイム署名（OTS）

Lamport署名

Winternitz署名（WOTS）

第7回耐量子暗号とこれからの暗号技術【連載：暗号技術の基礎を学ぶ】