CAMPFIRE Advent Calendar 2023 15日目の記事です。
こんにちは、CAMPFIRE Webエンジニアのhayashidaです。
今回はアドベントカレンダーということで、Web技術でもCAMPFIREでの開発についてでもなく、あえて普段の記事では書かない、量子コンピューティング技術にチャレンジしてみることにしてみました(私の知る限りでは、2023年12月現在、CAMPFIREで量子コンピューティング技術の応用は行っていません、あしからず…)。
手っ取り早くD-Waveを用いた量子プログラミングを知りたい場合には、量子プログラミングの項まで飛ばして読んでみてください。
量子コンピューティングとは
量子コンピューティングは、ミクロの世界の現象(量子力学)を用いて、これまでのノイマン型コンピュータなどと異なる計算プロセスでプログラムを実行するものです。
これにより、これまでスーパーコンピュータでも現実的な時間で解くことが難しかった素因数分解などの数学的問題や最適化問題、機械学習の高速化、検索問題、化学構造の研究などへの活用が期待されています(とはいえ、必要なレベルでいえば、最適化問題なども現実的な時間で古典的コンピュータでも解けるものも多くあります。また、既存のコンピュータを置き換えるものではない点も注意が必要です)。
また、これまでのコンピュータに比べて、理論的に消費電力や排熱も少なく済む(ランダウアーの原理等より)ため、近年話題になっているSDGsの観点からも一部注目されています。
量子コンピューティングをある程度理解するには「量子」「量子のふるまい」「量子ビット」「量子コンピュータの種類と現状」を知る必要があります。
量子プログラミングを行う上で各詳細を知る必要まではないので、すべてを理解できなくても問題ありません。ただし、量子コンピュータ以外のコンピュータとの違いを理解することで、特性に応じた処理を量子コンピュータに任せることができます。
量子(量子力学)とは
量子力学は、ミクロの世界の粒子(量子)のふるまいを研究する学問です。
このミクロの世界の粒子は、身の回りのマクロな世界のふるまいとは全く異なるふるまいをします。そのため、直感では非常に理解しにくい学問になっています。
量子
量子は、物理現象の最小単位を示すものです。
例えば、通常、明るさは連続的な値を取ると考えています。
一方、ミクロな世界で考えると、明るさに対応する光子(フォトン)という量子が存在していて、この光子の数で決まります。そのため、不連続な値を取ることになります。
ここでは明るさを、人間の目の光受容体で反応を起こすかどうかに最も関わる光量子束密度として説明しています。
量子として表されるものとして、光子(フォトン)や電子(エレクトロン)、中性微子(ニュートリノ)、原子、中性子や陽子、それらを構成する粒子などがあります。

ここまでで「光は波だと学校で習ったのに、粒子のように扱われている」ことに疑問を持った方もいるかと思います。ミクロの世界では、光や電子などは、粒子と波の両方の性質を持つことが知られています(このあとの「位相」の話にもつながります)。
ただし、これは「粒子が波のように振動して移動している」わけでも、「粒子が集まって波になっている」ことを意味しているわけではありません。理解するのが難しく、わたしたちの身の回りの粒子や波と異なる部分もあるため、とりあえずは「量子(光など)は、粒子の『性質』と波の『性質』両方を持っている」と思っておくのが良いかと思います。
このあたりのイメージの詳細は、二重スリット実験を調べてみてください。
参考:二重スリット実験 - Wikipedia
量子ビット(qubit、キュビット)
量子ビット(qubit) は、量子コンピューティングでの情報の基本単位です。
しかしながら、古典的なコンピューティングのビットとは異なり、取りうる状態すべての「重ね合わせ」を持つことができます。これにより、単純な0か1しか取れない場合に比べ、うまくアルゴリズムを組むことで、計算の途中で同時に複数の状態を考慮することができます(単純に0, 1の両方を並列計算できるわけではない点には注意です)。
※ 上記画像の重ね合わせは、あくまでイメージです。
重ね合わせ
普段の生活で、目の前にある時計が「観測するまでどこに存在するかわからない」というのは、馬鹿げた話に思えます。
一方で、ミクロな量子の世界では、粒子は取りうる状態すべての組み合わせである「重ね合わせ」の状態にあります。このとき、観測するまでこの粒子はどこに存在するか確定していないということがわかっています。これは計測装置の精度などの問題ではなく、わたしたちの生きるこの世界では量子の位置などの情報は本質的に予測できない、という意味です。このような量子の物理量(位置やエネルギーといった測定できる属性)が一定の範囲でばらつくことを「量子ゆらぎ」と言います(量子ゆらぎは、量子力学の根底にある概念で、量子コンピュータでも中心となる概念です)。
量子ビットに関して、この重ね合わせでは 0, 1のそれぞれが「どの程度実現されるか」の確率を保持することができます。ただし、その保持の仕方は単純な 10%、95%といったものではなく、「振幅」と呼ばれる値で保持されます。振幅を2乗すると確率になるので、振幅は負の値も取ることができます。
量子もつれ(エンタングルメント)
重ね合わせと同様に量子コンピュータにおける重要な量子特有のふるまいとして、「量子もつれ」があります。こちらは、複数の量子の間に強い相関を持つ状態を言います。
たとえば、2つの量子ビットがあったとします。これが片方が0ならもう片方も0、もう片方が1なら他方も1、というような関係を量子もつれによって生み出すことができるということです。
これにより、1つの量子ビットの操作で、もつれ状態の他の量子ビットも想定した形で操作することができます。このことにより、古典的なコンピュータであれば、ビット数が増えると指数関数的に処理時間が増加する場合でも、アルゴリズムによっては量子コンピュータではより少ない時間で計算できる場合が示されたりしています。
位相
位相とは、波の周期のうち、どのあたりにあるか、を示す値(物理量)です。
量子の説明の際に、ミクロな世界では量子が「粒子と波の両方の性質を持つ」と説明しました。そのため、量子ビットも波の性質としての「位相」を持ちます。
この位相は、確率には直接影響しません。そのため、量子ビットは位相が異なっていても振幅が同じであれば、0, 1 の出てくる確率は変わりません。
そのため、位相は直接確率に影響しない「観測前までに利用する情報」として利用されます。たとえば、計算途中で検索したいもの合致するアイテムにチェックをしておき、あとでそのチェックをもとに確率を上昇させておくといった用途です(これは、後述の量子ゲート方式でのGroverのアルゴリズムとして知られています)。
量子コンピュータの種類
すこし長くなりましたが、基本的な量子や量子ビットについて見てきたので、今度は量子コンピュータの種類について見ていきます。
現在の量子コンピュータは、量子ゲート方式と量子アニーリング方式の大きく2種類に分けられます。
量子ゲート方式 (狭義の量子コンピュータ)
量子ゲート方式のコンピュータは、 汎用的な用途を目的 とした量子コンピュータで、量子ゲートと呼ばれる回路の組み合わせによる量子計算を行います。
量子ビットになにを用いるか(超伝導量子、イオン、光子など)で、各国、各社や各研究所などで様々なコンピュータが開発されています。現在は外部からのノイズの低減やエラー訂正、計算量に影響する量子ビットの数を増やす大規模化の課題があるとされています。
一方で、2023年6月には、IBMなどで古典的なコンピュータでは解決の難しい現実の問題に対して、エラー訂正なしでも適用できる領域がある可能性が示されています。
https://jp.newsroom.ibm.com/2023-06-15-IBM-Quantum-Computer-Demonstrates-Next-Step-Towards-Moving-Beyond-Classical-Supercomputing
ちなみに、おそらく量子コンピュータ関連で最も聞いたことがある話の一つ、「量子コンピュータで、近い将来既存の暗号が解読される!」といった話は、こちらの方式によるものです(Shorのアルゴリズムと呼ばれています)。
量子アニーリング方式
量子アニーリング方式のコンピュータは、最適化問題に特化した量子コンピュータ1です。
最適化問題とは、ある条件の中で目的の関数が最大、または最小になる組み合わせを求める問題です。有名なものとしては、巡回セールスマン問題やナップザック問題などがあります。
早くから商用化されていることも特徴で、ゲート方式よりもエラー訂正の必要性が大きくないため、現実の問題への応用も進んでいます。しかしながら、こちらもまだ従来のコンピュータにくらべて全般的に高性能なわけではなく、現在の適用領域はそこまで広くないというのが実情です。
たとえば、従来でもGoogle Mapなど特定の日時に国内のA地点からB地点に行くといった際の最短経路を出してもらうと、多数の移動手段の中から現実的な時間で複数の経路を導き出してくれます。事前計算やアルゴリズム、クラウドの活用などでこうした複雑な最適化も実用レベルで対応できることが多いのも事実だと思われます。
ちなみにアニーリングとは、焼きなまし、という意味で、元々金属の熱をゆっくりと冷やしていくことで均質な構造にして金属を柔らかく加工しやすくする方法を言います。量子アニーリングも、量子を似たようなゆっくりとした変化をさせることで、最適化問題のより良い解を求めることができます(ここでの注意点としては、導き出せるのが厳密解ではなく、ヒューリスティックな解である点です)。
ただし、現在の量子アニーリングマシンでは「ゆっくりとした変化」という点では、あまり長い時間を取ることができないようです。これは重ね合わせの状態を維持できる時間が短いためです。そのため、基本的には繰り返し実行して、より良い値を解とするような仕組みになっています。
量子プログラミングを行う
ここまでで、量子コンピューティングの展望は広くあるものの、まだまだ研究段階でもあり、必ずしも従来のコンピュータを上回る性能を常に出せるわけでは無く、適用できる範囲もまだまだ狭いことがわかったかと思います。
とはいえ、今後のブレイクスルーにより、今のAIのように「誰もが当たり前に使っている時代」が来る可能性もあります。幸い、現在は比較的簡単に使える環境やシミュレータも整ってきているので、エンジニアとしてはここで一度触れてみるのも良い機会かと思います。今回は、そうした点で実際の量子コンピュータを利用するところまでチャレンジしてみることにしました。
量子アニーリング方式で最適化問題に取り組む
量子ゲート方式でも面白い問題に取り組むことができますが、個人レベルでは実用上の問題に適用しようとすると難しい部分もあります。そのため、量子アニーリング方式で最適化問題に取り組んでみることにします。
今回は、タイトルの通り、複数のタスクを複数チームに割り振るといった問題に挑戦してみます。
なお、量子ゲート方式に関しては、オライリーから出版されている「動かして学ぶ量子コンピュータプログラミング」などで実際のプログラミングを学ぶことができます(実践的でありながら、極力物理学の知識を使わずに説明しており、わかりやすい書籍です)。
量子アニーリング方式で問題の解を得るための流れ
量子アニーリング方式のコンピュータで問題の解を得るためには、以下のような流れでプログラミングをすることになります。
- 問題を定義する
- イジングモデルをQUBOで定式化する
- 実際のコードに落とし込む
- マシンで実行して、解を得る
2の定式化に関しては、サポートするライブラリなどでより直感的な定式化のままでコードに落とし込むこともできます。
1. 問題の定義: 複数のタスクを複数チームに割り振る
まずは問題を定義します。
今回は、複数のタスクを複数のチームに割り振ることを考えます。ただし、タスクすべてを割り当てる必要はなく、極力各チームの割り振れる最大に近くなるように割り振ります。
以下の条件でタスクをチームに割り振ります。
- チームの数: 3
- チームごとの割り振れる合計のタスクサイズの上限
- チーム1: 20
- チーム2: 15
- チーム3: 10
- タスク: 10個
- タスクサイズ: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
2. イジングモデルをQUBOで定式化する
イジングモデル、QUBOで定式化します。
ここで、説明がなかった「イジングモデル」「QUBO」という概念が出てきたので説明します。
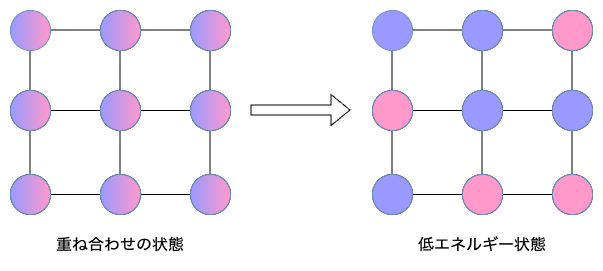
現在の量子アニーリング方式のコンピュータは、私が知る限りでは概ねイジングモデルを活用しています。イジングモデルは、2種類の状態を取るミクロな要素が格子上に並んでいる模型(イメージは量子アニーリング方式の項を参照)で、物理学で磁石などの物質の性質を説明するために導入されたものです。量子アニーリング方式のコンピュータでは、このイジングモデルに解きたい問題を変換した初期状態から、磁場をかけつつ低エネルギー状態に移行させて、この低エネルギーの状態を解に変換する、という手順で問題の解を求めます。
量子アニーリング方式のコンピュータは、CPUなどのコンピュータとは異なり、計算処理のプロセスというよりは物理的な状態の変化を用いて解を探索するという手法を取っています(そのため、量子アニーリング方式は量子コンピュータではないという説明も見かけます)。
QUBOは「Quadratic Unconstrained Binary Optimization」の略で日本語では「二次制約なし二値最適化」と呼ばれます。QUBOはイジングモデルと対応しており、解きたい問題を直接イジングモデルに置き換えるより簡単なため、活用されています。
QUBOでの定式化に関しては、ある種のテクニックが必要になるため、自分で行う場合にはそうしたテクニックを知っておく必要があります。こちらに関しては、量子アニーリング利用のための定式化方法紹介 が参考になります。
ここから、QUBOをコードに落としこむ必要もあるため、一般化した数式が出てきます。そこまで複雑な数式ではないですが、我慢して読みすすめていただければと思います。プログラミングに慣れている場合は、後で紹介するコード部分と対比すると、どのような数式か理解しやすいかもしれません。
前提条件の記述
まずは、前提条件を一般化した数式で表現していきます。
タスクが $N$ 個あり、それぞれがタスクサイズ $L_i$ を持つとします。
すると、 各タスクのサイズのリスト $L$ は以下で表せます。
$$L = \lbrace L_1, L_2, \dots, L_N \rbrace$$
チームが複数あり、割当可能な上限がそれぞれのチームで異なっています。そこで、チーム数を $S$ 、各チームの割当可能な上限を $M_i$ とします。
チーム $\alpha$ に割り振られたタスクのインデックスのリスト $V_\alpha$ から、チーム $\alpha$ に割り振られたタスクの合計サイズ $T_\alpha$ は、以下となります。
$$T_\alpha = \sum_{i\in V_\alpha} L_i \le M_\alpha$$
ただし、このままではQUBOでは表現できていないため、チーム $\alpha$ で i番目のタスクを割り当てる場合 $1$ 、割り当てない場合 $0$ とする変数 $x_{i,\alpha}$ を定義して書き直します。
$$
\begin{align}
&T_\alpha = \sum_i L_i x_{i,\alpha} \le M_\alpha \tag{1} \\
&x_{i,\alpha} \in \lbrace 0, 1 \rbrace \tag{2} \\
&(\forall \alpha \in \lbrace 1, 2, \dots S\rbrace) \
\end{align}
$$
目的関数
目的となる数式を定義します。
前項で記載した数式 $(1)$ から、以下を最小化するのが目的になります。
$$\sum_j \left(\sum_i L_i x_{i,j}\right) - M_j\tag{3}$$
制約条件
制約条件となる数式を定義します。
各チームの割り当て上限を超えないことがあります。
$(1)$ では不等式として表現されているため、そのままではQUBOで定式化できません。そのため、ここでスラック変数を導入して、定式化します。
スラック変数は不等式による制約を等式の制約に変換するための変数です(スラック変数の詳細については補足の項で説明します)。
スラック変数 $y_i$ を用いることで、制約を以下のように書き換えます。
$$M_\alpha - \sum_i L_i x_{i,\alpha} - \sum_{n=1}^{\log_2(M_\alpha-1)+1}2^ny_n = 0 \tag{4}$$
また、ほかのチームで割り当て済みのタスクを割り当てることはできないため、以下の制約もあります。
$$\sum_i \sum_j \sum_{k\ne j} x_{i,j}x_{i,k} = 0 \tag{5}$$
QUBOの定式化
目的関数 $(3)$ と制約条件 $(4), (5)$ からQUBOで定義します。
$$
\begin{align}
H &= k_oH_o + k_{c1}H_{c1} + k_{c2}H_{c2} \\
H_o &= \sum_j \left(\sum_i L_i x_{i,j}\right) - M_j \\
H_{c1} &= \sum_j \left(M_j - \sum_i L_i x_{i,j} - \sum_{n=1}^{\log_2(M_j-1)+1}2^ny_n\right)^2 \\
H_{c2} &= \sum_i \sum_j \sum_{k\ne j} x_{i, j} x_{i, k}
\end{align}
$$
ただし、制約条件を違反しないために、$k_o$, $k_{c1}$, $k_{c2}$ は以下の制約を満たすようにします。
$$0 < k_o \max(L_i) < k_{c1}, k_{c2}$$
実際の問題に合わせる
ここまでは一般化して話してきたので、実際のチーム数やタスクに合わせて書き直します。
$$
\begin{align}
N &= 10\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (タスク数)\\
L &= \lbrace 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \rbrace\ \ \ \ (各タスクサイズ)\\
S &= 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (チーム数)\\
M &= \lbrace 20, 15, 10 \rbrace \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (各チームの割り当て上限)\\\\\\
H &= k_{o}H_o + k_{c1}H_{c1} + k_{c2}H_{c2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (QUBO定式化)\\
H_o &= \sum_j^S \left(\sum_i^N L_i x_{i,j}\right) - M_j\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (目的関数)\\
H_{c1} &= \sum_j^S \left(M_j - \sum_i^N L_i x_{i,j} - \sum_{n=1}^{\log_2(M_j-1)+1}2^ny_n\right)^2\ \ \ \ (制約条件1)\\
H_{c2} &= \sum_i \sum_j \sum_{k\ne j} x_{i, j} x_{i, k}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (制約条件2)\\
&x_{i,j}, y_n \in \lbrace 0, 1 \rbrace \\
&0 < k_o \max{L_i} < k_{c1}, k_{c2}
\end{align}
$$
3. 実際のコードに落とし込む
実際のコードに落とし込んでいきます。
まず初めに、今回は pyQUBO、OpenJij で SA(Simulated Annealing)、SQA(Simulated Quantum Annealing)を実行してみます(ここで出せるのは、古典的なアニーリングのシミュレーションと、古典的なコンピュータ上での量子シミュレーションによる結果です)。
pyQUBOで計算する
ここからは Python3 はインストール済みとして記載していきます。
まずは pyqubo、openjij、numpyをインストールします。
$ pip install pyqubo openjij numpy
つぎに各種前提条件を設定していきます。
import numpy as np
# チームの割り当て上限
teams = [20, 15, 10]
# チームの数
team_count = len(teams)
# タスクサイズ
tasks = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# タスクの数
task_count = len(tasks)
つぎに変数を設定します。
スラック変数は導入時の定義からチーム $\alpha$ では $\lfloor \log_2 (M_\alpha - 1) \rfloor+1$ 個必要になります
from pyqubo import Array,LogEncInteger
slack_size = [6, 5, 5]
x = Array.create('x', shape=(task_count, team_count), vartype='BINARY')
ys = [LogEncInteger('y',(0, i)) for i in slack_size]
ここから、目的関数と制約条件を表現していきます。
from pyqubo import Constraint
kc2 =55
kc1 = (kc2 / max(tasks) ** 2) / 0.5
ko = (kc2 / max(tasks)) / 5.5
# 目的項
Ho = sum(sum(tasks[i] * x[i, j] for i in range(task_count)) - teams[j] for j in range(team_count))
# 制限項
const1 = 0
for j in range(team_count):
const1 += (teams[j] - sum(tasks[i] * x[i, j] for i in range(task_count)) + ys[j]) ** 2
Hc1 = Constraint(const1, label='Hc1')
const2 = 0
for i in range(task_count):
const2 += sum(sum(x[i, j] * x[i, k] if j != k else 0 for k in range(team_count)) for j in range(team_count))
Hc2 = Constraint(const2, label='Hc2')
H = ko * Ho + kc1 * Hc1 + kc2 * Hc2
そして、以下のように SAで評価してみます。
# pyQUBOで SAで評価する
from pyqubo import solve_qubo
import neal
model = H.compile()
qubo, offset = model.to_qubo()
sampler = neal.SimulatedAnnealingSampler()
raw_solution = sampler.sample_qubo(qubo, num_reads=500)
decoded_sample = model.decode_sample(raw_solution.first.sample, vartype="BINARY")
job_length = [0] * team_count
for i in range(0, team_count):
print("チーム" + str(i + 1) + "で行われるタスク")
for j in range(0, task_count):
if decoded_sample.array('x', (j, i)) == 1:
print(" " + str(j + 1) + "番目のタスク サイズ:" + str(tasks[j]))
job_length[i] += tasks[j]
print(" タスクの合計サイズ:" + str(job_length[i]))
print()
print("broken:")
print(decoded_sample.constraints(only_broken=True))
すると以下のような出力が得られます。
チーム1で行われるタスク
3番目のタスク サイズ:3
8番目のタスク サイズ:8
9番目のタスク サイズ:9
タスクの合計サイズ:20
チーム2で行われるタスク
2番目のタスク サイズ:2
6番目のタスク サイズ:6
7番目のタスク サイズ:7
タスクの合計サイズ:15
チーム3で行われるタスク
10番目のタスク サイズ:10
タスクの合計サイズ:10
broken
{}
重複なく、各割り当て上限を満たすように割り当てられていることがわかります。
OpenJij で計算する
OpenJijでのSQAの場合も同様にハミルトニアンの定義までは行います。その上で、以下のようにコードを書きます。
# OpenJijで SQAで評価する
import openjij as oj
sampler = oj.SQASampler()
response = sampler.sample_qubo(Q=qubo, num_reads=300)
dict_solution = response.first.sample
decoded_sample = model.decode_sample(raw_solution.first.sample, vartype="BINARY")
job_length = [0] * team_count
for i in range(0, team_count):
print("チーム" + str(i + 1) + "で行われるタスク")
for j in range(0, task_count):
if decoded_sample.array('x', (j, i)) == 1:
print(" " + str(j + 1) + "番目のタスク サイズ:" + str(tasks[j]))
job_length[i] += tasks[j]
print(" タスクの合計サイズ:" + str(job_length[i]))
print()
print("broken:")
print(decoded_sample.constraints(only_broken=True))
出力としては、pyQUBOと同様の結果が出力されます。
4. マシンで実行して解を得る
最後に実際のマシン上でQA(Quantum Annealing)を実行してみます。
今回は D-Wave で実行します。初回登録後1ヶ月間は1分間の無料利用が付与されます(短く感じますが、簡単なものであれば、必要な回数を余裕で実行できます)。
D-Wave Leapに登録後、Dashboardに表示されるAPIトークンを取得しておきます。
また、以下のページから、対象のリージョンのエンドポイントも確認しておきます。
https://docs.ocean.dwavesys.com/en/stable/overview/sapi.html
まずは、 dwave-ocean-sdk をインストールします。
$ pip install dwave-ocean-sdk
次にpythonでトークン、エンドポイントを定数に設定しておきます。今回、トークンは環境変数から読み込むようにしています。エンドポイントは2023年11月現在の北米リージョンのものです。
import os
DWAVE_TOKEN = os.getenv('DWAVE_TOKEN')
DWAVE_ENDPOINT = "https://na-west-1.cloud.dwavesys.com/sapi/v2/"
最後にpyQUBOで実装した際の変数 qubo を利用して、D-Waveに投げて実行してみます。今回は繰り返しの回数を1000回にします(事前に疎通確認したい場合は 補足の項を参照)。
from dwave.system import DWaveSampler, EmbeddingComposite
sampler = EmbeddingComposite(
DWaveSampler(token=DWAVE_TOKEN,
endpoint=DWAVE_ENDPOINT,
solver='Advantage_system4.1')
)
response = sampler.sample_qubo(qubo, num_reads=1000)
最後に結果を確認します。
# 結果を全件表示(1000回分全て表示されるので、ファイル出力などが望ましい)
# print(response.record)
# 最も良い結果を表示
print(response.first)
出力結果は以下となりました(実行ごとに変わる可能性があります)。
Sample(sample={
'x[0][0]': 0, 'x[0][1]': 0, 'x[0][2]': 0,
'x[1][0]': 0, 'x[1][1]': 0, 'x[1][2]': 0,
'x[2][0]': 1, 'x[2][1]': 0, 'x[2][2]': 0,
'x[3][0]': 0, 'x[3][1]': 1, 'x[3][2]': 0,
'x[4][0]': 0, 'x[4][1]': 1, 'x[4][2]': 0,
'x[5][0]': 0, 'x[5][1]': 1, 'x[5][2]': 0,
'x[6][0]': 0, 'x[6][1]': 0, 'x[6][2]': 0,
'x[7][0]': 1, 'x[7][1]': 0, 'x[7][2]': 0,
'x[8][0]': 1, 'x[8][1]': 0, 'x[8][2]': 0,
'x[9][0]': 0, 'x[9][1]': 0, 'x[9][2]': 1,
'y[0]': 0, 'y[1]': 0, 'y[2]': 0},
energy=-752.5000000000002, num_occurrences=1,
chain_break_fraction=0.0)
結果の見方としては、 x[i][j] は チームj+1 に、タスクi+1 が割り当てられたことを示します。
今回は、パラメータ調整を行った結果、正しい良い結果が得られました。
ただし、残念ながら今回のレベルであれば、古典的コンピュータのアニーリングシミュレーションのほうがより簡単に精度良い結果を出せている結果となりました。
まとめ
今回は、量子コンピュータの基礎となっている物理的な現象の概要と、量子コンピュータの種類、現実の問題(最適化問題)に適用しやすい量子アニーリング方式のコンピュータでのプログラムの実行を行ってみました。
量子コンピューティングはまだまだ研究レベルに近く、社会問題や企業活動等での課題解決で活用していくまでには超える必要のある課題も多くあるかと思います。また、現在利用されているノイマン型コンピュータ上でも、アルゴリズムや最適化、複数のハードウェアの活用などにより、量子コンピュータが得意とされている領域でも、現実的な問題のサイズであれば十分に解決できる場合も多々あります。
一方、技術的なブレイクスルーにより、専門性の高い領域や、機械学習の領域、また電力消費や排熱の課題などで既存のコンピュータと並行して活用されていく可能性もあります。
今回実行したのは実用性が高いプログラムではありませんが、個人でも実際のマシンで量子コンピューティングを実行できる現状を知ることができました。また、(イジングモデルでの)量子アニーリング方式に関して、どういった手順でプログラムを作成・実行できるかも理解できました。
今回試したD-Wave以外にもAWSやAzureなどの大手クラウドでも量子コンピューティングを実行できます(こちらは量子ゲート方式を基本的に提供しているようです)。興味がある方はぜひチャレンジしてみてください(通常利用することの多いEC2などのコンピューティングサービスに比べると時間あたりの料金はかかるので、その点は注意してください)。
また、今回調べた中でQUBOで定式化することなく、より直感的な条件の数式をそのままコードで表現することで記載できるライブラリ等も存在するとのことでした。そうしたライブラリ等を活用することで、より量子コンピューティングもやりやすくなるのではないかと思います。
最後に、個人的には、今回実機上で実行するところまでできた点はかなり良かったかと思います。D-Waveに関しては現在、初回登録後1ヶ月間は一定時間分は無料で利用できるのと、手元でシミュレーションで実行したうえでそのコードを適用することができるので、チャレンジしやすいなと感じました。
次に機会があれば、量子ゲート方式にもチャレンジしてみたいと思います。
補足
スラック変数について
説明の際にスラック変数は、詳細を省いて導入しました。そのため、ここで簡単に説明をしたいと思います。
スラック変数は、最適化問題で、制約条件である不等式を等式の制約で表現できるようにするために導入する変数です。
たとえば、以下のような制約条件があったとします。
$$x_1 + 2x_2 + 3x_3 \le 3$$
このままではQUBOに組み込めないため、 $0$か$1$を取るスラック変数 $y_1, y_2$ を用いて等式の形式の制約に書き換えます。
$$x_1 + 2x_2 + 3x_3 + 2^0y_1 + 2^1y_2 = 3$$
このようにすると、 $x_1 + 2x_2 + 3x_3 \le 3$ を満たす場合は、
| $x_1$ | $x_2$ | $x_3$ | $y_1$ | $y_2$ | $x_1+2x_2+3x_3 + 2^0y_1+2^1y_2$ |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 3 |
| 1 | 0 | 0 | 0 | 1 | 3 |
| 0 | 1 | 0 | 1 | 0 | 3 |
| 0 | 0 | 1 | 0 | 0 | 3 |
| 1 | 1 | 0 | 0 | 0 | 3 |
のようになるため、スラック変数を用いることで不等式だった制約を等式の形式に書き換えることができます。
D-Waveへの疎通確認
D-Waveへの疎通確認を事前にする際には以下のようにできます。
まずは dwave-ocean-sdk をインストールします。
pip install dwave-ocean-sdk
その後、D-Waveのトークンを取得したうえで、以下を実行します。
from dwave.cloud import Client
import os
DWAVE_TOKEN = os getenv('DWAVE_TOKEN') # 環境変数 DWAVE_TOKEN に設定済みの想定
client = Client.from_config(token=DWAVE_TOKEN)
print(client.get_solvers())
上記を実行すると、D-WaveのAPIと疎通できれば、利用可能なソルバーが返却、表示されます。この段階では、量子コンピュータなどは利用していないため、無料枠は減少しません。
-
今回は、"コンピュータ"としていますが、解を求める手順などからすると一般的な感覚ではマシンといったほうが近いかもしれません。しかし、今回は広義の量子"計算機"(= コンピュータ)とさせていただきます。 ↩





