1. はじめに

逆強化学習について勉強したので、備忘録として残します。
強化学習、逆強化学習、模倣学習に分類することができます。

技術名	入力	出力	アルゴリズム
強化学習	報酬とシミュレーター	最適方策	DQN
逆強化学習	最適方策とシミュレーター	報酬	線形計画
逆強化学習	エキスパートの行動履歴とシミュレーター	報酬	Maximum Entoropy
模倣学習	エキスパートの行動履歴とシミュレーター	最適方策・報酬	GAIL

Ziebart, Mass, Bagnell and DeyのMaximum Entropy Inverse Reinforcement Learningをもとに説明します。

2. エキスパートの行動軌跡の特徴量の定式化

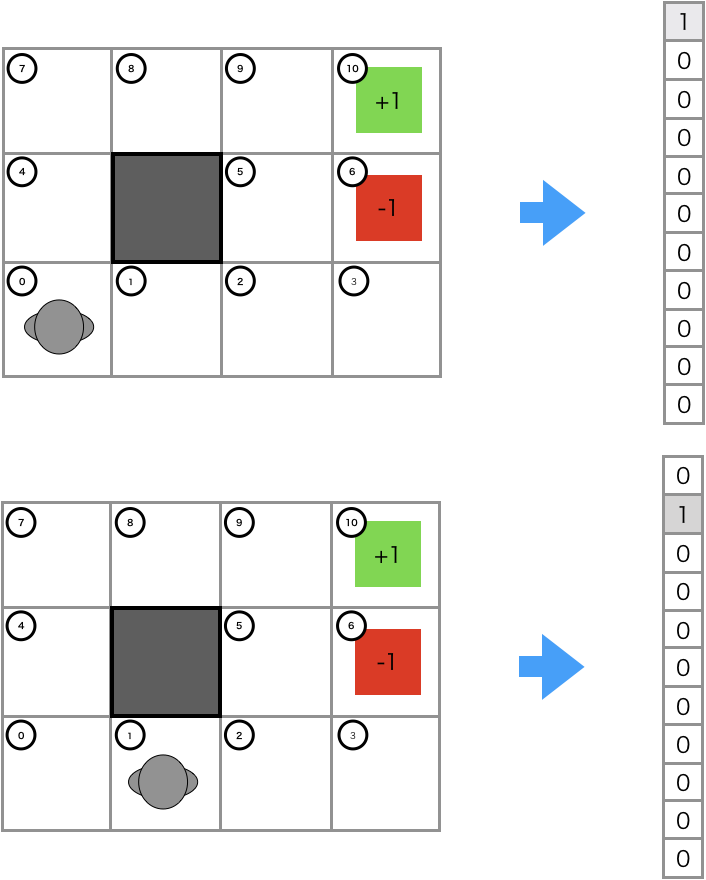
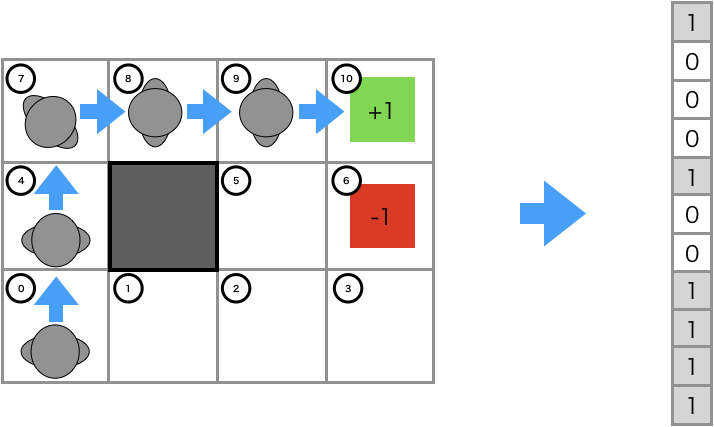
エキスパートが状態$s$において行動$a$を$T$回行ったことを記録した行動軌跡$\zeta$があるとします。

\zeta = \lbrace (s_1,a_1),(s_2,a_2),\cdots,(s_T,a_T)\rbrace

エキスパートの行動軌跡の特徴量$\mathbf{f}_\zeta$を定式化することを考えます。

まず、状態$s$における特徴量$\mathbf{f}_s$を表すone-hotベクトルを導入します。

行動軌跡の特徴量$\mathbf{f}_\zeta$は、行動軌跡で訪れた状態$s$のone-hotベクトルの総和として定式化します。

\mathbf{f}_\zeta = \sum_{s\in\zeta}\mathbf{f}_s

図は下の記事から参照させて頂きました。

$M個の$エキスパートの行動軌跡は、エキスパートの行動履歴$D$に格納されています。

D=\lbrace\zeta_1,\zeta_2,\cdots,\zeta_M\rbrace

3. 報酬の関数近似

報酬を、エキスパートの行動軌跡の特徴量$\mathbf{f}_\zeta$とパラメータ$\theta$で関数近似することを考えます。

R(\zeta|\theta)=\theta^T\mathbf{f}_\zeta

パラメータ$\theta$を推定できれば、状態$s$の特徴量$\mathbf{f}_s$から、状態$s$の報酬$R(s)$が定まります。

R(s)=\hat{\theta}^T\mathbf{f}_s

$R(s)$こそが、Maximum Entorpyで求めたい報酬関数になります。

4. 報酬関数のパラメータΘの推定

報酬関数のパラメータ$\theta$を求めることを考えます。

最大エントロピー原理を適用して、行動軌跡の発生確率$P(\zeta|\theta)$の解析解を求めた後、行動軌跡の発生確率$P(\zeta|\theta)$の解析解をもとに最尤推定により$\theta$を推定します。

4.1 最大エントロピー原理

行動軌跡の発生確率$P(\zeta|\theta)$はどうあるべきでしょうか？

エキスパートの行動履歴の制約条件にして、エキスパートの行動履歴で想定していない事象については、確率$P(\zeta|\theta)$をできるだけ等しく割り当てればよさそうです。

目的関数にエントロピー最大化を適用することで、確率$P(\zeta|\theta)$をできるだけ等しく割り当てます。

また、等式制約で、行動軌跡の特徴量$\mathbf{f_\zeta}$の条件付き期待値が、観測した行動軌跡の特徴量$\mathbf{f}_{\zeta}$の期待値と一致するように追加することで、エキスパートの行動履歴を制約条件として考慮できるようにしています。

\begin{eqnarray}
\max &  & -\sum_{\zeta\in D} P(\zeta|\theta)\log P(\zeta|\theta)\\

\mathrm{s.t.} & &\sum_{\zeta\in D}P(\zeta|\theta)\mathbf{f}_\zeta=\mathbb{E}[\mathbf{f}_\zeta]\\
     & &\sum_{\zeta\in D}P(\zeta|\theta) = 1
\end{eqnarray}

ラグランジュの未定乗数法により、確率$P(\zeta|\theta)$は解析解を得ます。

P(\zeta|\theta)
=\dfrac{\exp(\theta^T\mathbf{f_\zeta})}{\sum_{\zeta\in D}\exp(\theta^T\mathbf{f_\zeta}))}
=\dfrac{\exp(R(\zeta|\theta))}{\sum_{\zeta\in D}\exp(R(\zeta|\theta))}

これは、報酬$R(\zeta|\theta)$が大きくなるほど、行動軌跡の発生確率$P(\zeta|\theta)$が大きくなることを表しています。

式変形は下の記事を参照ください。

4.2 最尤推定

尤度関数$L(\theta)$を考えます。

L(\theta) = \frac{1}{M}\sum_{i=1}^{M}\log P(\zeta_i|\theta)

以下のように、パラメータ$\theta$を更新することで、尤度最大化を図ります。

\theta_{k+1} \leftarrow \theta_k + \alpha\dfrac{\partial L(\theta)}{\partial \theta}

エキスパートの行動軌跡の特徴量の平均値と、$\theta$に基づいて行動した場合の行動軌跡の特徴量の平均値が一致するように、パラメータ$\theta$を更新しています。

\dfrac{\partial L(\theta)}{\partial \theta}=\frac{1}{M} \sum_{i=1}^M {\mathbf{f}_{\zeta_i}} - \sum_{i=1}^M P(\zeta_i|\theta) { \mathbf{f}_{\zeta_i}}

4.3 最尤推定の式変形の補足

\begin{eqnarray}
L(\theta) &=& \frac{1}{M} \sum_{i=1}^M \log P(\zeta_i|\theta) \\
  &=& \frac{1}{M} \sum_{i=1}^M \log \frac{{\rm exp}(R(\zeta_i|\theta))}{\sum_{j=1}^M {\rm exp}(R(\zeta_j|\theta))} \\
  &=& \frac{1}{M} \sum_{i=1}^M R(\zeta_i|\theta) - \log \sum_{i=1}^M \exp R(\zeta_i|\theta) \\
  &=& \frac{1}{M} \sum_{i=1}^M \theta^{\rm T}\mathbf{f}_{\zeta_i} - \log \sum_{i=1}^M \exp \theta^{\rm T}\mathbf{f}_{\zeta_i} \\
\end{eqnarray}

\begin{eqnarray}
\frac{\partial L(\theta)}{\partial \theta} 
   &=& \frac{\partial}{\partial \theta}  \biggl( \frac{1}{M} \sum_{i=1}^M \theta^{\rm T}\mathbf{f}_{\zeta_i} - \log \sum_{i=1}^M \exp \theta^{\rm T}\mathbf{f}_{\zeta_i} \biggr) \\
   &=& \frac{1}{M} \sum_{i=1}^M \mathbf{f}_{\zeta_i} -  \frac{1}{\sum_{i=1}^M \exp \theta^{\rm T}\mathbf{f}_{\zeta_i}} \frac{\partial}{\partial \theta} \sum_{i=1}^M \exp \theta^{\rm T}\mathbf{f}_{\zeta_i} \\
   &=& \frac{1}{M} \sum_{i=1}^M \mathbf{f}_{\zeta_i} - \sum_{i=1}^M \frac{\exp \theta^{\rm T}\mathbf{f}_{\zeta_i}}{\sum_{j=1}^M \exp \theta^{\rm T}\mathbf{f}_{\zeta_i}}\mathbf{f}_{\zeta_i} \\
   &=& \frac{1}{M} \sum_{i=1}^M \mathbf{f}_{\zeta_i} - \sum_{i=1}^M P(\zeta_i|\theta)\mathbf{f}_{\zeta_i}\\
\end{eqnarray}

4.4 アルゴリズム

step 1. $\theta$に初期値を代入する。
step 2. 各状態$s$を特徴量$\mathbf{f_s}$に変換する。
step 2. エキスパートの行動軌跡$\zeta$から特徴量$\mathbf{f_\zeta}$に変換する。
step 3. 報酬関数$R(s|\theta)=\theta^T\mathbf{f}_s$を算出する。
step 4. 強化学習を用いて最適方策$\pi(・|s,\theta)$を推定する。
step 5. 最適方策$\pi(・|s,\theta)$から状態$s_i$に訪れる確率$P(s_i|\theta)$を算出する。
step 6. 最尤推定により$\theta$を更新する。
step 7. step 3.に戻る。

状態$s_i$に訪れる確率$P(s_i|\theta)$を求めることは容易ではないため、実装ではひと工夫をしているようです。

5. 参考文献

機械学習スタートアップシリーズ Pythonで学ぶ強化学習 [改訂第2版] 入門から実践まで、久保隆宏
Pythonではじめる逆強化学習
日本一詳しくMaximumEntropyIRLのソースコードを解説してみる
Maximum Entropy IRL（最大エントロピー逆強化学習）とその発展系について
逆強化学習を理解する

逆強化学習【Maximum Entropy】