1. はじめに
最近、逆強化学習について勉強しているので備忘録がわりにソースコードの解説をしようと思います。こちらで解説するのは逆強化学習の中で基礎的かつメジャーな手法であるMaximum Entropy IRLになります。こちらの手法はQiitaの記事や書籍にも分かりやすい解説がすでにあるので二番煎じ感はありますが、それでもいくつか悩んだところがあったため、改めて解説していきます。
2. 解説するソースコード
「Pythonで学ぶ強化学習」の逆強化学習に関するサンプルコードを使用させて頂いて解説を行います。
3. そもそも逆強化学習(IRL)とは
逆強化学習とは強化学習で使う報酬関数を実軌跡データから推定する問題設定になります。
一般的な強化学習(モデルフリーな)の場合
- エージェントが環境の状態$s_t$を観測する
- 方策$\pi(a_t|s_t)$に従い、行動$a_t$を行う
- 行動の結果変化した環境の状態$s_{t+1}$を観測する
- 報酬関数$R$から状態$s_{t+1}$の際の報酬を獲得し、方策を改善する
という作業を繰り返すことで報酬関数的に適切な方策を獲得します。
状態と行動と報酬関数は設計者が決める必要があります。ここで問題となるのがエージェントに行なって欲しいタスクを報酬関数として適切に表現するのが難しい場合が多い、ということです。そこで活躍するのが逆強化学習となります。

逆強化学習では報酬関数をパラメータで表現し、望ましい軌跡のデータ(エキスパートデータ)$\zeta=\{s_0, a_0, s_1, a_1, \cdots, s_{t-1}, a_{t-1}, s_t\}$から報酬関数のパラメータを推定します。推定された報酬関数を用いて強化学習を行うことで、望ましい軌跡を実現できる方策が獲得できると期待されます。
4. Maximum Entropy IRLの理論
4.1 報酬関数
まずMaximum Entropy IRLの概要について説明します。
こちらの手法では報酬関数を以下のようにパラメータの線形関数で定義します。
$$
R(\zeta | \theta) = \theta^{\rm T} \boldsymbol {\rm f}_{\zeta} = \sum_{s \in \zeta} \theta^{\rm T} \boldsymbol {\rm f}_{s}
$$
ここで$\theta$はパラメータの列ベクトル、$\textbf{f}_\zeta$は特徴ベクトルの列ベクトルであり、報酬関数$R(\zeta)$はそれらの内積(線形和)をとったものになります。また、$\Sigma$の下の$s \in \zeta$は望ましい軌跡のデータ$\zeta$に含まれる全ての状態$s$.という意味になります。
この報酬関数のパラメータをある条件を満たすよう推定します。
4.2 特徴ベクトル
今回解説するコードで扱う環境は以下の16マスのグリッドワールドになります。ここでマスの番号が状態の番号、緑色が報酬1、赤色が報酬-1を意味しています。
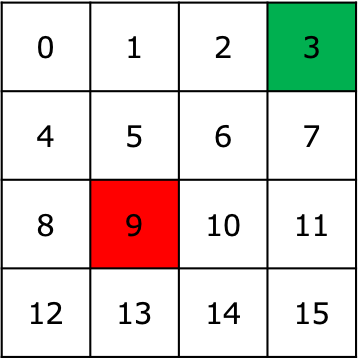
こちらの環境の場合、特徴ベクトル$\textbf{f}_\zeta$は16次元の列ベクトルで表し、各対応する要素は1
、それ以外の要素は0で表現します。
例えば状態6(マスの番号6)の特徴ベクトルは
$$\textbf{f}_{s=6}=[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]^{\rm T}$$
となります。
ここで、軌跡データ$\zeta=\{s_0=12, s_1=13, s_2=12, s_3=8, s_4=4, s_5=0, s_6=1, s_7=2, s_8=3 \}$の場合、この軌跡の特徴ベクトルは
$$
\boldsymbol {\mathrm f}_{\zeta}=\boldsymbol {\mathrm f}_{s_0} + \boldsymbol {\mathrm f}_{s_1} + \boldsymbol {\mathrm f}_{s_2} + \dots + \boldsymbol {\mathrm f}_{s_8} = [1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0]^{\rm T}
$$
となります。
こちらの例では軌跡データは1つですが、実際は軌跡データは複数個用いますのでご注意ください。
4.3 推定した報酬関数が満たすべき条件
報酬関数のパラメータを推定するにあたっての方針としては、推定された報酬関数から獲得した方策による軌跡の特徴ベクトルとエキスパート軌跡の特徴ベクトルを出来るだけ近づくようにすることです。

式で書くと以下のように、軌跡の期待値を一致させることになります。
$$
\mathbb{E}[f_\zeta] = \mathbb{E}[f_{\zeta-expert}]
$$
ここで、推定した報酬関数を用いて獲得した方策によって取得できる軌跡の分布を$P(\zeta)$として導入します。こちらは尤度とも呼ばれます。尤度$P(\zeta)$は推定した報酬関数から獲得されるため、パラメータ$\theta$に依存しますので、$P(\zeta | \theta)$とも書けます。ここからは報酬関数$R(\zeta|\theta)$を推定する代わりに$P(\zeta | \theta)$を推定することで$\theta$を決定していくことになります。
上式の軌跡の期待値を一致させる$P(\zeta | \theta)$はいくつも存在しますので、さらに制約条件を追加します。その制約条件というのが$P(\zeta | \theta)$のエントロピー最大化であり、手法のタイトルの由来になります。
ここでエントロピーとは情報量の大小を表す値で、エントロピーが大きいとは情報量が大きいこと、エントロピーが小さいとは情報量が小さいことを意味します。情報量というのは予測が難しい事柄について知った場合は情報量が大きくなります。
例えば①梅雨時期に明日が雨という情報を得る場合、②梅雨時期以外に明日が雨という情報を得る場合、を比較すると梅雨時期以外の方が雨が降る確率が低く予測が難しいため
$$
①のエントロピー < ②のエントロピー
$$
となります。
離散分布の場合は均一分布(サイコロの目の確率のような)がエントロピー最大となります。
話を戻して$P(\zeta | \theta)$のエントロピー最大化というのはエキスパートデータからわかる情報以外については情報がないため、出来るだけ均等に発生するようにしよう、というものです。「出来るだけ均等に」と言うのはエントロピー最大化を目指すと言うことになります。これを式で書くと以下のようになります。ここで$Z=\{\zeta_0, \zeta_1, \dots\}$であり、軌跡の集合になります。
$$
max \sum_{\zeta \in Z} P(\zeta|\theta) {\mathrm log} P(\zeta|\theta)
$$
制約条件としては
①軌跡の期待値が一致
$$
\sum_{\zeta \in Z} P(\zeta|\theta) {\mathrm f_\zeta} = \mathbb{E}[f_\zeta]
$$
②$P(\zeta | \theta)$は確率分布
$$
\sum_{\zeta \in Z} P(\zeta|\theta) = 1
$$
であり、これを考慮してラグランジュの未定乗数を用いて解くと
$$
P(\zeta|\theta) = \frac{{\rm exp}(R(\zeta|\theta))}{\sum_{\zeta \in Z} {\rm exp}(R(\zeta|\theta))}
$$
という報酬関数$R(\zeta)$のsoftmax関数の形となり、軌跡の発生確率が報酬に指数比例しています。
4.4 パラメータの推定
$P(\zeta | \theta)$の式形状を決めることが出来たので、最尤推定法を用いてパラメータを推定します。ここではエキスパートの軌跡データはM個としています。
\begin{eqnarray}
\theta^* &=& {\rm arg~max}_{\theta} \sum_{i=1}^M \log P(\zeta_i|\theta) \\
&=& {\rm arg~max}_{\theta} \frac{1}{M} \sum_{i=1}^M \log P(\zeta_i|\theta) \\
&=& {\rm arg~max}_{\theta} \frac{1}{M} \sum_{i=1}^M \log \frac{{\rm exp}(R(\zeta_i|\theta))}{\sum_{j=1}^M {\rm exp}(R(\zeta_j|\theta))} \\
&=& {\rm arg~max}_{\theta} \biggl( \frac{1}{M} \sum_{i=1}^M R(\zeta_i|\theta) - \log \sum_{i=1}^M \exp R(\zeta_i|\theta) \biggr) \\
&=& {\rm arg~max}_{\theta} \biggl( \frac{1}{M} \sum_{i=1}^M \theta^{\rm T}{\rm f_{\zeta_i}} - \log \sum_{i=1}^M \exp \theta^{\rm T}{\rm f_{\zeta_i}} \biggr) \\
&=& {\rm arg~max}_{\theta} \biggl( L(\theta) \biggr)
\end{eqnarray}
こちらの式の最適値を解析的に求めるのが難しいため、勾配法を用いてパラメータを推定します。上式のカッコ内の$L(\theta)$を最大化するパラメータを求めたい為、以下の勾配を計算します。
\begin{eqnarray}
\frac{\partial L(\theta)}{\partial \theta} &=& \frac{\partial}{\partial \theta} \biggl( \frac{1}{M} \sum_{i=1}^M \theta^{\rm T}{\rm f_{\zeta_i}} - \log \sum_{i=1}^M \exp \theta^{\rm T}{\rm f_{\zeta_i}} \biggr) \\
&=& \frac{1}{M} \sum_{i=1}^M {\rm f_{\zeta_i}} - \frac{1}{\sum_{i=1}^M \exp \theta^{\rm T}{\rm f_{\zeta_i}}} \frac{\partial}{\partial \theta} \sum_{i=1}^M \exp \theta^{\rm T}{\rm f_{\zeta_i}} \\
&=& \frac{1}{M} \sum_{i=1}^M {\rm f_{\zeta_i}} - \sum_{i=1}^M \frac{\exp \theta^{\rm T}{\rm f_{\zeta_i}}}{\sum_{j=1}^M \exp \theta^{\rm T}{\rm f_{\zeta_j}}} {\rm f_{\zeta_i}} \\
&=& \frac{1}{M} \sum_{i=1}^M {\rm f_{\zeta_i}} - \sum_{i=1}^M P(\zeta_i|\theta) {\rm f_{\zeta_i}} \\
\end{eqnarray}
ここで軌跡$\zeta$は状態$s$の状態列なので、上式を以下のように$s$を用いて書き換えることができます。
\begin{eqnarray}
\frac{\partial L(\theta)}{\partial \theta} &=& \frac{1}{M} \sum_{i=1} {\rm f_{s_i}} - \sum_{i=1} P(s_i|\theta) {\rm f_{s_i}}
\end{eqnarray}
この式はエキスパート軌跡の特徴ベクトルの平均値と推定したパラメータによる尤度を用いた期待値を近づけることでパラメータが最適化されることを意味しています。言い換えるとエキスパートが各状態を訪れる確率と推定したパラメータによる尤度により各状態を訪れる確率の差を計算すれば良いということです。各状態にいる頻度を表す16次元の列ベクトルを$\mu$とします。
そうすると上式の代わりに
\begin{eqnarray}
\frac{\partial L(\theta)}{\partial \theta} &=& \mu_{export} - \mu(\theta)
\end{eqnarray}
で勾配を計算できます。ここで$\mu(\theta)$は状態遷移確率とパラメータから推定された方策から計算できます。
$\mu(\theta)$のs行目を$\mu(s|\theta)$として、あるtステップ目に状態sに訪れる頻度を$\mu_t(s|\theta)$とすると、
$$
\mu_t(s|\theta) = \sum_{a \in A} \sum_{s' \in S} \mu_{t-1}(s'| \theta) \pi(a|s', \theta)P(s|a, s')
$$
となります。
5. ソースコード
処理手順は以下の通りです。
- パラメータの初期化
- エキスパートデータから特徴ベクトルを計算
- パラメータを用いて報酬関数を計算
- 計算した報酬関数から方策を計算
- 計算した方策で特徴ベクトルを取得
- 勾配を計算してパラメータを更新
- 3~6を指定したエポック繰り返す
以下にソースコードを示します。
import numpy as np
from planner import PolicyIterationPlanner
from tqdm import tqdm
class MaxEntIRL():
def __init__(self, env):
self.env = env
self.planner = PolicyIterationPlanner(env)
def estimate(self, trajectories, epoch=20, learning_rate=0.01, gamma=0.9):
# 特徴量行列 F
# 16×16の単位行列
state_features = np.vstack([self.env.state_to_feature(s)
for s in self.env.states])
# 1. パラメータθを初期化
theta = np.random.uniform(size=state_features.shape[1])
# 2. エキスパートデータから特徴ベクトルに変換
teacher_features = self.calculate_expected_feature(trajectories)
for e in tqdm(range(epoch)):
# Estimate reward.
# 3. 状態ごとの報酬関数 R(s) = θ・F
rewards = state_features.dot(theta.T)
# 現時点のパラメータによる報酬関数を設定
self.planner.reward_func = lambda s: rewards[s]
# 4. 現時点の報酬関数に対して、方策を計算
self.planner.plan(gamma=gamma)
# 5. 計算した方策で特徴ベクトルを取得
features = self.expected_features_under_policy(
self.planner.policy, trajectories)
# 6. 勾配を計算
# μ_expert - μ(θ)
update = teacher_features - features.dot(state_features)
theta += learning_rate * update
estimated = state_features.dot(theta.T)
estimated = estimated.reshape(self.env.shape)
return estimated
def calculate_expected_feature(self, trajectories):
'''
エキスパートデータから特徴ベクトルを作成する関数
:param trajectories: エキスパートの軌跡データ
:return: 特徴ベクトル
'''
features = np.zeros(self.env.observation_space.n)
for t in trajectories:
for s in t:
features[s] += 1
features /= len(trajectories)
return features
def expected_features_under_policy(self, policy, trajectories):
'''
パラメータによる報酬関数から獲得される方策による特徴ベクトルの取得
:param policy: 方策
:param trajectories: エキスパート軌跡 軌跡数×状態のリスト
:return: 各状態の発生確率 16次元のリスト
'''
# エキスパート軌跡の数, このコードではt_size=20
t_size = len(trajectories)
states = self.env.states
# 状態遷移確率 軌跡の数×状態数
transition_probs = np.zeros((t_size, len(states)))
# 状態の発生確率(各状態の到達頻度)
initial_state_probs = np.zeros(len(states))
# 各軌跡データの初期状態を取得して、数をカウント
# 今回の場合は初期状態は12の為、transition_probs[12]=20でそれ以外は0
for t in trajectories:
initial_state_probs[t[0]] += 1
# 回数を頻度に変換するためにt_sizeで割る
initial_state_probs /= t_size
# 状態遷移確率の初期行に初期状態の配列を代入
transition_probs[0] = initial_state_probs
# 環境の状態遷移確率にしたがって,t_size-1回状態遷移を繰り返して状態の発生確率を計算
# 疑問なのが、なぜ繰り返すステップ数がt_sizeで良いのか?
for t in range(1, t_size):
# 1ステップ前の状態prev_sが状態0~15の場合をそれぞれ計算
# 1ステップ前の状態の発生確率と状態遷移確率を掛けて全て足すことで今ステップの状態発生確率を計算
# μ_t(s') = P(s'|s, a) * Σμ_t-1(s)
for prev_s in states:
# 1ステップ前に状態prev_sにいる確率を計算
prev_prob = transition_probs[t - 1][prev_s]
# 1ステップ前の状態prev_sで行う行動を方策から決定
a = self.planner.act(prev_s)
# 状態遷移確率に従い、各状態への遷移確率を取得. probsは16次元のリスト.
probs = self.env.transit_func(prev_s, a)
# 1ステップ前の発生確率と状態遷移確率を掛ける
for s in probs:
transition_probs[t][s] += prev_prob * probs[s]
# t_sizeステップ分の発生確率を平均して、各状態の発生確率を計算
total = np.mean(transition_probs, axis=0)
return total
if __name__ == "__main__":
def test_estimate():
# 環境の設定
from environment import GridWorldEnv
env = GridWorldEnv(grid=[
[0, 0, 0, 1],
[0, 0, 0, 0],
[0, -1, 0, 0],
[0, 0, 0, 0],
])
# エキスパートデータの収集
teacher = PolicyIterationPlanner(env)
teacher.plan()
trajectories = []
print("Gather demonstrations of teacher.")
for i in range(20):
s = env.reset()
done = False
steps = [s]
while not done:
a = teacher.act(s)
n_s, r, done, _ = env.step(a)
steps.append(n_s)
s = n_s
trajectories.append(steps)
# 逆強化学習を実行
print("Estimate reward.")
irl = MaxEntIRL(env)
rewards = irl.estimate(trajectories, epoch=100)
print(rewards)
env.plot_on_grid(rewards)
test_estimate()
6. Maxmum Entropy IRLの注意点
- 離散状態の必要がある
状態を訪れる頻度から特徴ベクトルを計算する為、基本的には離散状態を前提としています
- モデルベースの手法(状態遷移確率が必要)
状態を訪れる頻度$\mu$を計算する際に状態遷移確率が必要な為、基本的にはモデルベースの手法となります。