逆強化学習
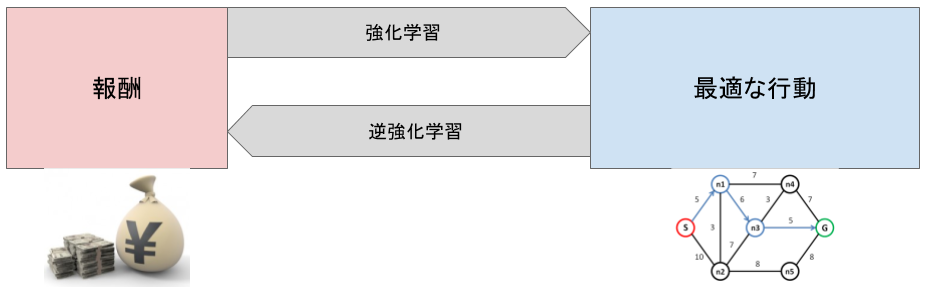
一般的な強化学習では、エージェントが環境からの報酬を得ることで最適な行動を獲得します。しかし現実の問題においては、この報酬を設計することが困難な場合があります。
例えば運転技術を獲得する場合、うまい運転というのはただ目的地に速く着くだけでなく、急発進・急ブレーキしない、混んでなさそうな道を選ぶなど実際の報酬関数として考慮しづらい要素が存在します。 逆強化学習ではエキスパートによる行動から報酬を推定する ことによって、このような表現しにくい報酬を求めることができます。
逆強化学習の手法
この記事では逆強化学習の手法としてよく取り上げられる手法の中で以下の3つについて解説したいと思います。
- 線形計画法を用いた逆強化学習
- Maximum Entropy IRL
- Maximum Entropy Deep IRL
マルコフ決定過程(MDP)
逆強化学習に入る前にまずMDPについて説明します。
マルコフ決定過程は簡単には $(S, A, T, R)$ の組みからなる確率的な過程を示します。
- $S(=1,2,...,M) $ : 有限状態空間
- $A$ : 状態$i \in S $でとり得るアクションの有限集合
- $T$ : 状態$i$で行動$a \in A $をとったとき、つぎの時刻で状態$j \in S $に遷移する確率
- $R$ : 状態$i$で行動$a$をとったときの期待即時コスト
今回はMDPとしてよく使われるGrid Worldを環境として使用します。OpenAI Gymを使ったものがすでに存在するのでこれを使います。
インポートして実行すると以下のように動きます。実行結果のxがエージェントの現在位置を示しています。
import gridworld
env = gridworld.GridworldEnv()
env.render()
env.step(gridworld.UP)
env.render()
env.step(gridworld.LEFT)
env.render()
実行結果
T o o o
o o o o
o x o o
o o o T
T o o o
o x o o
o o o o
o o o T
T o o o
x o o o
o o o o
o o o T
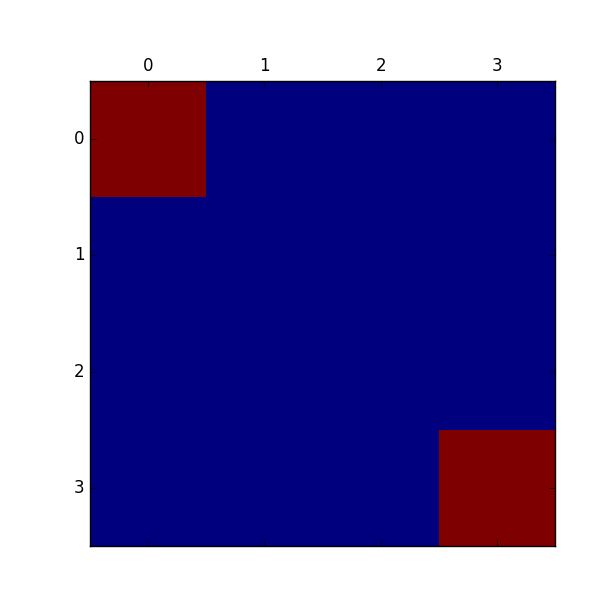
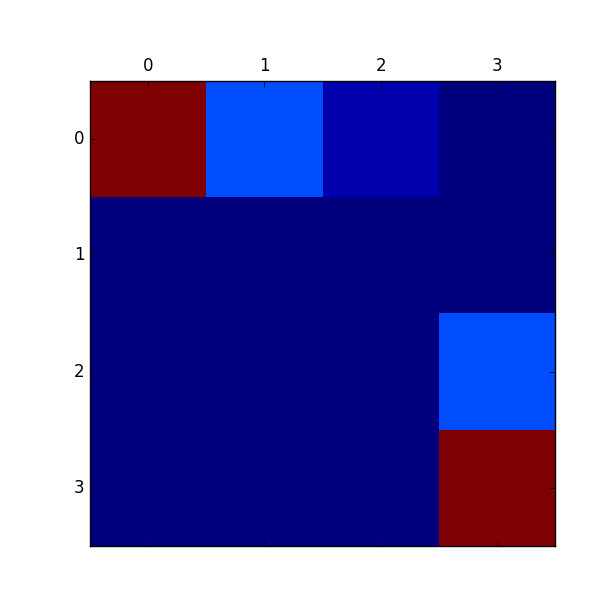
また報酬のマップは以下のようになります。赤が報酬が高い、青が報酬が低いところです。
価値反復法
MDPにおいて最適な価値関数$V^*(s)$を求めるベルマンの最適方程式は以下のように書けます。
V^*(s)=\max_a \Bigl( R(s,a) + \gamma \sum_{s'} P(s'|s,a)V^*(s') \Bigr)
今回は報酬関数を状態のみの関数にしようと思っているので、以下のように$\max$が後ろの項にのみかかります。
V^*(s)= R(s) + \gamma \max_a \Bigl( \sum_{s'} P(s'|s,a)V^*(s') \Bigr)
この式を上で作成したGrid環境に適応し、全状態の最適な価値を求められる関数は以下のようになります。
def value_iteration(trans_probs, reward, gamma=0.9, epsilon=0.001):
"""Solving an MDP by value iteration."""
n_states, n_actions, _ = trans_probs.shape
U1 = {s: 0 for s in range(n_states)}
while True:
U = U1.copy()
delta = 0
for s in range(n_states):
Rs = reward[s]
U1[s] = Rs + gamma * max([sum([p * U[s1] for s1, p in enumerate(trans_probs[s, a, :])])
for a in range(n_actions)])
delta = max(delta, abs(U1[s] - U[s]))
if delta < epsilon * (1 - gamma) / gamma:
return U
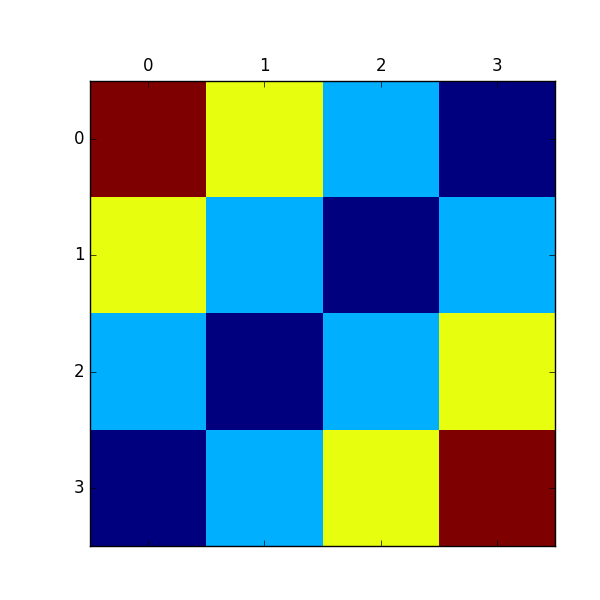
この関数を用いて、各状態での価値を描画したものが下図になります。
次に求めた価値関数から最適な方策を求めます。最適な価値$V^*$を用いて求める方策の式は以下のようになります。
\pi (s) = arg \max_{a \in A} \sum_{s'} P(s'|s,a)V^*(s')
コードは以下のようになります。
def expected_utility(a, s, U, trans_probs):
"""The expected utility of doing a in state s, according to the MDP and U."""
return sum([p * U[s1] for s1, p in enumerate(trans_probs[s, a, :])])
def best_policy(trans_probs, U):
"""
Given an MDP and a utility function U, determine the best policy,
as a mapping from state to action.
"""
n_states, n_actions, _ = trans_probs.shape
pi = {}
for s in range(n_states):
pi[s] = max(range(n_actions), key=lambda a: expected_utility(a, s, U, trans_probs))
return pi
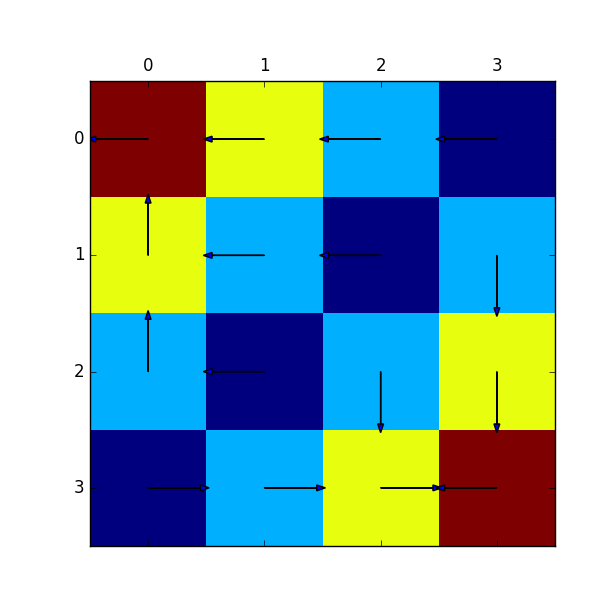
これを用いて実際に各状態での最適な方策を描画したものが下図になります。ゴールの矢印は初期値のままなので無視してもらって、それ以外は実際にゴールに向かうように矢印が流れているのが分かると思います。
線形計画法を用いた逆強化学習
まず最初にNgらによる線形計画法を用いた逆強化学習について説明します。
ここでは逆強化学習では各状態$s_i(i=1,2,...,M)$における最適な行動$a_1$(上で計算した方策)が既知であるとします。このとき各状態における報酬を表したベクトル$R$を求めます。これは以下のような最適化を解く問題になります。
\begin{equation}
\begin{split}
maximize:& \sum_{i \in S} \min_{a \in A \setminus a_1} \Bigl\{ \bigl(P_{a_1}(i) - P_a(i) \bigr) {\bigl(I - \gamma P_{a_1}(i) \bigr)}^{-1} R \Bigr\} - \lambda ||R||_1 \\
subject:& \bigl(P_{a_1}(i) - P_a(i) \bigr) {\bigl(I - \gamma P_{a_1}(i) \bigr)}^{-1} R \geq 0 \\
& |R_i| \leq R_{max}
\end{split}
\end{equation}
この式の意味について少し考えてみます。
この式の中で重要なのは$\bigl(P_{a_1}(i) - P_a(i) \bigr) {\bigl(I - \gamma P_{a_1}(i) \bigr)}^{-1} R$の部分になります。
これは最適な行動$a_1$とそれ以外の行動の期待報酬の差を求めています。つまりこの 目的関数は$a_1$との期待報酬の差が最も小さい行動(2番めに良い行動)との期待報酬の差を最も大きくするような報酬ベクトル を求めていることになります。
上の式はこの状態では線形計画問題として扱うことができないので、新たに$t_i, u_i$という変数を用意し以下のように変換します。
\begin{equation}
\begin{split}
maximize:& \sum_{i \in S} \bigl\{ t_i - \lambda u_i \bigr\} \\
subject:& \bigl(P_{a_1}(i) - P_a(i) \bigr) {\bigl(I - \gamma P_{a_1}(i) \bigr)}^{-1} R \geq t_i \\
& \bigl(P_{a_1}(i) - P_a(i) \bigr) {\bigl(I - \gamma P_{a_1}(i) \bigr)}^{-1} R \geq 0 \\
& -u \leq R \leq u \\
& |R_i| \leq R_{max}
\end{split}
\end{equation}
これをコード化してみます。
import numpy as np
from scipy.optimize import linprog
def lp_irl(trans_probs, policy, gamma=0.2, l1=1.5, Rmax=5.0):
"""
Solve Linear programming for Inverse Reinforcement Learning
"""
n_states, n_actions, _ = trans_probs.shape
A = set(range(n_actions))
tp = np.transpose(trans_probs, (1, 0, 2))
ones_s = np.ones(n_states)
eye_ss = np.eye(n_states)
zero_s = np.zeros(n_states)
zero_ss = np.zeros((n_states, n_states))
T = lambda a, s: np.dot(tp[policy[s], s] - tp[a, s], np.linalg.inv(eye_ss - gamma * tp[policy[s]]))
c = -np.r_[zero_s, ones_s, -l1 * ones_s]
zero_stack = np.zeros((n_states * (n_actions - 1), n_states))
T_stack = np.vstack([-T(a, s) for s in range(n_states) for a in A - {policy[s]}])
I_stack = np.vstack([np.eye(1, n_states, s) for s in range(n_states) for a in A - {policy[s]}])
A_ub = np.bmat([[T_stack, I_stack, zero_stack], # -TR <= t
[T_stack, zero_stack, zero_stack], # -TR <= 0
[-eye_ss, zero_ss, -eye_ss], # -R <= u
[eye_ss, zero_ss, -eye_ss], # R <= u
[-eye_ss, zero_ss, zero_ss], # -R <= Rmax
[eye_ss, zero_ss, zero_ss]]) # R <= Rmax
b = np.vstack([np.zeros((n_states * (n_actions-1) * 2 + 2 * n_states, 1)),
Rmax * np.ones((2 * n_states, 1))])
results = linprog(c, A_ub, b)
return results["x"][:n_states]
この関数を使って、線形計画法によって得られる報酬マップを求めてみます。関数の引数trans_probsは状態遷移確率を示しておりGrid環境内にあるメンバ変数Pから求めることができます。policyは上の価値反復法から求めた最適方策を用います。
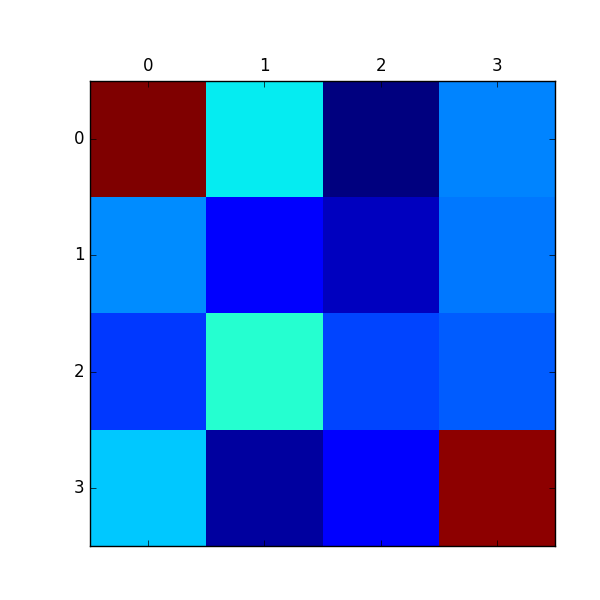
実際に推定した結果を描画したものが下図になります。正解は上の報酬マップのように左上と右下のみに色が付けば良いですが、それなりに推定できているようです。
Maximum Entropy IRL
Maximum Entropy IRLでは報酬関数$r(s)$をパラメタ$\theta$を用いて以下のような線形関数で近似します。
r_{\theta}(s) = {\theta}^T\phi(s)
ここで$\phi(s) \in R^{|S|}$は特徴ベクトルといって、状態$s$を表現する特徴量です。今回は単純にone-hotベクトルを用います。
このときMaximum Entropy IRLでは熟練者は以下のような確率で経路$\zeta=[(s_0, a_0),(s_1, a_1),...,(s_T, a_T)]$を選択していると仮定します。
P(\zeta |\theta ) = \frac{\exp{(R_{\theta}(\zeta ))}}{Z}
ここで、
R_{\theta}(\zeta ) = \sum_t r_{\theta}(s_t) \\
Z=\sum_{\zeta} \exp{(R_{\theta}(\zeta ))}
上式を用いて最適な$N$個の行動列$D=[ {\zeta}^{(0)} , {\zeta}^{(1)} ,..., {\zeta}^{(N)} ]$が与えられた際に、以下の対数尤度関数$L(\theta)$を最大にする$\theta$を求めることで報酬関数を推定します。
L(\theta) = -\sum_i \log P({\zeta}^{(i)}| \theta )
尤度最大化を行うために$L(\theta)$の勾配を求めます。
L(\theta) = -\sum_i \log \frac{\exp{(R_{\theta}({\zeta}^{(i)} ))}}{Z} = \sum_i R_{\theta}({\zeta}^{(i)} ) - N \log{Z} = \sum_i R_{\theta}({\zeta}^{(i)} ) - N \log \sum_i \exp{(R_{\theta}({\zeta}^{(i)}))} \\
\begin{eqnarray}
{\nabla}_{\theta} L(\theta) &=& \sum_i \frac{dR_{\theta}({\zeta}^{(i)} )}{d\theta} - N \frac{1}{\sum_i \exp{(R_{\theta}({\zeta}^{(i)}))}} \sum_i \exp{(R_{\theta}({\zeta}^{(i)}))} \frac{dR_{\theta}({\zeta}^{(i)})}{d\theta} \\
&=& \sum_i \frac{dR_{\theta}({\zeta}^{(i)} )}{d\theta} - N \sum_i \frac{\exp{(R_{\theta}({\zeta}^{(i)}))}}{\sum_i \exp{(R_{\theta}({\zeta}^{(i)}))}} \frac{dR_{\theta}({\zeta}^{(i)})}{d\theta} \\
&=& \sum_i \frac{dR_{\theta}({\zeta}^{(i)} )}{d\theta} - N \sum_i P({\zeta}^{(i)}| \theta ) \frac{dR_{\theta}({\zeta}^{(i)})}{d\theta} \\
&=& \sum_s \frac{dr_{\theta}(s)}{d\theta} -N \sum_s p(s | \theta ) \frac{dr_{\theta}(s)}{d\theta}
\end{eqnarray}
ここで$p(s | \theta )$はstate visitation freqencyと呼ばれており、状態$s$を訪れた頻度を表しています。
これらを踏まえて、Maximum Entropy IRLのコードは以下のようになります。
import numpy as np
from value_iteration import *
def expected_svf(trans_probs, trajs, policy):
n_states, n_actions, _ = trans_probs.shape
n_t = len(trajs[0])
mu = np.zeros((n_states, n_t))
for traj in trajs:
mu[traj[0][0], 0] += 1
mu[:, 0] = mu[:, 0] / len(trajs)
for t in range(1, n_t):
for s in range(n_states):
mu[s, t] = sum([mu[pre_s, t - 1] * trans_probs[pre_s, policy[pre_s], s] for pre_s in range(n_states)])
return np.sum(mu, 1)
def max_ent_irl(feature_matrix, trans_probs, trajs,
gamma=0.9, n_epoch=20, alpha=0.5):
n_states, d_states = feature_matrix.shape
_, n_actions, _ = trans_probs.shape
feature_exp = np.zeros((d_states))
for episode in trajs:
for step in episode:
feature_exp += feature_matrix[step[0], :]
feature_exp = feature_exp / len(trajs)
theta = np.random.uniform(size=(d_states,))
for _ in range(n_epoch):
r = feature_matrix.dot(theta)
v = value_iteration(trans_probs, r, gamma)
pi = best_policy(trans_probs, v)
exp_svf = expected_svf(trans_probs, trajs, pi)
grad = feature_exp - feature_matrix.T.dot(exp_svf)
theta += alpha * grad
return feature_matrix.dot(theta)
Maximum Entropy IRLでは熟練者の経路が必要であり、上の関数の引数trajsがそれに当たります。
熟練者による経路は最適方策を用いて以下のように計算するようにしました。
def generate_demons(env, policy, n_trajs=100, len_traj=5):
trajs = []
for _ in range(n_trajs):
episode = []
env.reset()
for i in range(len_traj):
cur_s = env.s
state, reward, done, _ = env.step(policy[cur_s])
episode.append((cur_s, policy[cur_s], state))
if done:
for _ in range(i + 1, len_traj):
episode.append((state, 0, state))
break
trajs.append(episode)
return trajs
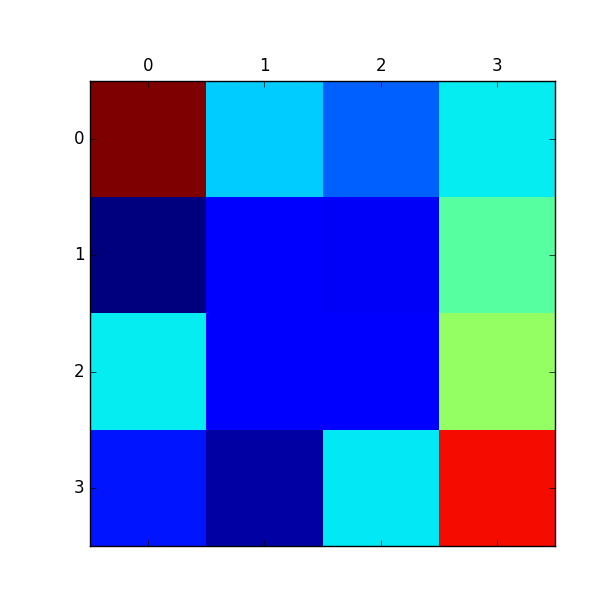
生成した経路を用いてMaximum Entropy IRLによって報酬を推定した結果が以下になります。
こちらもまあまあ推定できています。LPを使った方法と違って、 実際の最適な方策まで分かってなくても熟練者からの軌道列のみを用いて推定できる のがメリットと言えます。
Maximum Entropy Deep IRL
Maximum Entropy IRLと深層学習を組み合わせた手法がこれになります。通常のMaximum Entropy IRLでは線形関数によって報酬関数$r(s)$を近似しましたが、これをニューラルネットで表現したものに置き換えます。
ネットワークの更新のために、最適化を行う尤度関数を以下のように熟練者の経路による項と正則化項に分離します。
L(\theta)=\log P(D, \theta|r) = \underbrace{\log P(D|r)}_{L_D} + \underbrace{\log P(\theta)}_{L_{\theta}}
この尤度関数の$L_D=\log P(D|r)$のパラメタ微分を求めて式変形することで、楽に勾配を求めることができます。
式変形を少し端折りますが、実際には以下のような勾配を求めることになります。
\frac{\partial L_D(\theta)}{\partial \theta} = (\mu_D - E[\mu]) \frac{\partial r_{\theta}(s)}{\partial \theta}
ここで、上式の$\mu_D$は熟練者の経路から求めた状態頻度で、$E[\mu]$は状態頻度の期待値を表します。
コードはほぼMaximum Entropy IRLと同じ形になります。報酬関数がニューラルネットに変更され、それに伴いパラメタ更新のところなどが変わっています。今回、深層学習部分の実装にはChainerを用いています。
import numpy as np
import chainer
import chainer.links as L
import chainer.functions as F
from chainer import optimizers
from value_iteration import *
from max_ent_irl import *
class Reward(chainer.Chain):
def __init__(self, n_input, n_hidden):
super(Reward, self).__init__(
l1=L.Linear(n_input, n_hidden),
l2=L.Linear(n_hidden, n_hidden),
l3=L.Linear(n_hidden, 1)
)
def __call__(self, x):
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
return self.l3(h2)
def max_ent_deep_irl(feature_matrix, trans_probs, trajs,
gamma=0.9, n_epoch=30):
n_states, d_states = feature_matrix.shape
_, n_actions, _ = trans_probs.shape
reward_func = Reward(d_states, 64)
optimizer = optimizers.AdaGrad(lr=0.01)
optimizer.setup(reward_func)
optimizer.add_hook(chainer.optimizer.WeightDecay(1e-4))
optimizer.add_hook(chainer.optimizer.GradientClipping(100.0))
feature_exp = np.zeros((d_states))
for episode in trajs:
for step in episode:
feature_exp += feature_matrix[step[0], :]
feature_exp = feature_exp / len(trajs)
fmat = chainer.Variable(feature_matrix.astype(np.float32))
for _ in range(n_epoch):
reward_func.zerograds()
r = reward_func(fmat)
v = value_iteration(trans_probs, r.data.reshape((n_states,)), gamma)
pi = best_policy(trans_probs, v)
exp_svf = expected_svf(trans_probs, trajs, pi)
grad_r = feature_exp - exp_svf
r.grad = -grad_r.reshape((n_states, 1)).astype(np.float32)
r.backward()
optimizer.update()
return reward_func(fmat).data.reshape((n_states,))
本来は尤度関数に正則化項を足す必要があるのですが、同じような効果があるWeight Decayに置き換えています。
いろいろとチューニングしてみて思ったのは、最適化はAdamのほうが安定している気がしましたが、論文に基づいて今回はAdaGradのままで最適化しています。
こちらも報酬マップが推定できているのがわかります。
感想
深層学習を使えば簡単に精度よく推定できるのかと思いましたが、それなりにチューニングは必要でした。
論文だともっと複雑な報酬マップに対して、深層学習を使った手法だけが格段に推定できているので、今回の環境よりももっと複雑な環境でやってみると明らかな差が出るのかなと思いました。
発展・応用
GANとの関連やロボットに応用したGuided Cost Learningなどの発展的内容にも注目していきたいです。
- A Connection between Generative Adversarial Networks, Inverse Reinforcement Learning, and Energy-Based Models
- Guided Cost Learning
使用したコード
今回使用したコードはすべてgithubにあげています。
https://github.com/neka-nat/inv_rl
参考文献
- TensorFlowで逆強化学習
- これからの強化学習
- Algorithm for Inverse Reinforcement Learning
- Maximum Entropy Inverse Reinforcement Learning
- Maximum Entropy Deep Inverse Reinforcement Learning
- 自然言語処理における逆強化学習・模倣学習の適用
- Inverse Reinforcement Learning
- https://github.com/stormmax/irl-imitation
- https://github.com/MatthewJA/Inverse-Reinforcement-Learning