1. はじめに
本記事ではこの論文で提案されている逆強化学習の基礎的な手法であるMaximum Entropy IRLを解説していきます。逆強化学習は強化学習をベースにしており、理解するためには強化学習の基礎知識が必要です。強化学習の基礎部分に不安がある方は、必要な基礎知識を前の記事でまとめましたのでよろしければそちらをご覧ください。
2. 逆強化学習とは
逆強化学習の目的は、優秀なエージェント(エキスパート)の行動軌跡$\zeta$から、報酬関数$R(s)$を求めることです。エキスパートはあるタスクを達成できるエージェントです。行動軌跡とは、エキスパートの一連の行動を表す状態と行動のペアの系列のことです。式で次のように表すことができます。
$$
\zeta = \{(s_1,a_1),(s_2,a_2),\cdots,(s_t,a_t),\cdots,(s_T,a_T)\}
$$
$s$は状態、$a$は行動を表し、エキスパートは$T$回行動を取ったことになります。報酬関数は、ある状態$s$が与えられるとその良さを返す関数です。逆強化学習では、エキスパートの行動系列をいくつかサンプルし、そのサンプルから報酬関数$R(s)$を求めます。
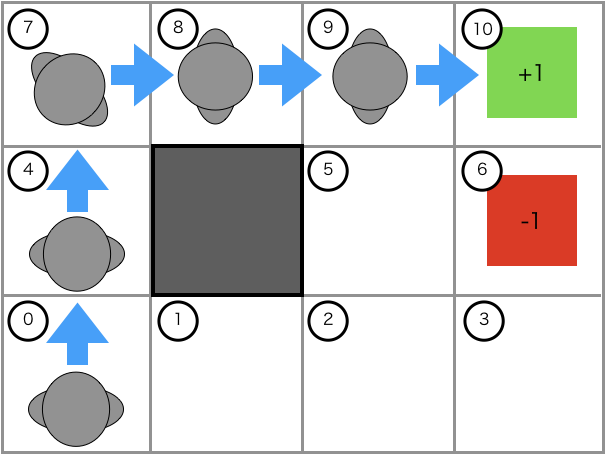
逆強化学習を下図の迷路を例に考えてみます。
図中の番号は状態を表し、エージェントが選択可能な行動は(↑、↓、←、→)であるとします。青い線で表されたエキスパートの行動軌跡$\zeta$は、
$$
\zeta = \{(0,↑),(4,↑),(7,→),(8,→),(9,→)\}
$$
となります。エキスパートのスタート地点を変えるなどして、行動軌跡をいくつかサンプルします。$M$個サンプルしたとすると、次のようになります。
$$
{\rm examples} = \{\zeta_1,\zeta_2,\cdots,\zeta_i,\cdots,\zeta_M \}
$$
$M$個のサンプルから報酬関数が次のように求まれば、逆強化学習の目的を達成したことになります。
$$
\begin{eqnarray}
R(s) =
\begin{cases}
1 & {\rm if}\ s=10 \
-1 & {\rm if}\ s=6 \
0 & {\rm otherwise}
\end{cases}
\end{eqnarray}
$$
この報酬関数はエージェントの状態が、10のとき$+1$、6のとき$-1$、それ以外のとき$0$の報酬を返します。上の図に対応させると、緑のブロックで$+1$、赤のブロックで$-1$、それ以外のブロックで$0$の報酬が得られることを表します。
3. Maximum Entropy IRLの理論
3.1 最大エントロピー原理
最大エントロピー原理は、観測されたデータからある制約条件のもとで、エントロピーが最大となるように確率分布を推定する手法です。エントロピーとは情報の不確実性を表しており、高ければ情報がより不確実であることを表します。天気を例として考えます。明日の天気が晴れか雨か全くわからない時、すなわち不確実性が最も高い場合、晴れと雨の確率はそれぞれ$1/5$になります。このときのエントロピーは
$$
H=- \frac{1}{5} \log \frac{1}{5} - \frac{1}{5} \log \frac{1}{5} = 0.69
$$
となります。逆に天気が晴れとわかっている時、すなわち不確実性が最も低い場合、エントロピーは、
$$
H = - 1 \times \log 1 = 0
$$
となります。
エントロピーを最大化するのは、観測されなかった事象に対しては極力一様に確率を割り振るためです。観測データは、すべての事象を含んでいるとは限らないので、当然観測されなかったデータもあるはずです。観測されなかった事象は、不確実性が高いので、エントロピーは高くなります。すなわち観測されなかった事象に対して、一様に確率を割り振ることになります。
3.2 報酬関数の推定
エキスパートの行動軌跡から、報酬関数を推定する手法であるMaximum Entropy IRLでは求める報酬関数を
$$
R(\zeta) = \theta^{\rm T} \boldsymbol {\rm f}_{\zeta} = \sum_{s \in \zeta} \theta^{\rm T} \boldsymbol {\rm f}_{s}
$$
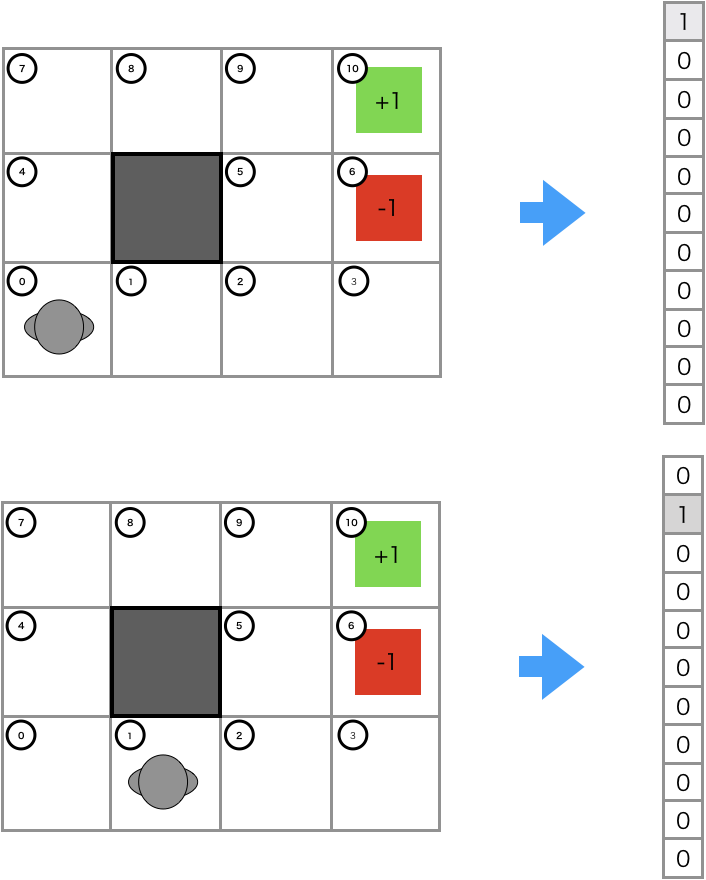
と定義します。エキスパートの行動履歴の特徴量$\boldsymbol {\mathrm f}_{\zeta}$と、パラメータ$\theta$の内積により、報酬関数を表しています。$\theta$は逆強化学習の手法によって最適化するパラメータで、$\boldsymbol {\rm f}_{\zeta}$は行動軌跡の特徴量、$\boldsymbol {\rm f}_s$は状態$s$の特徴量です。状態$s$の特徴量を図で表すと以下のようになります。
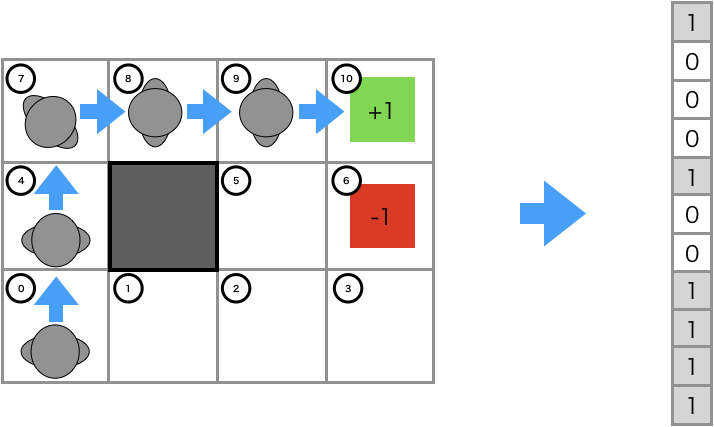
図の上段で示したのは、状態0での特徴量で$\boldsymbol {\mathrm f}_0=(1,0,0,0,0,0,0,0,0,0,0)^{\mathrm T}$です。状態の番号に該当する要素の値が1、それ以外は0になっています。いわゆるone-hotベクトルです。 行動軌跡の特徴量は下図のようになります。
各状態の特徴量ベクトルを要素ごとに足し合わせたベクトルになっていることがわかります。数式で表すと、
$$
\boldsymbol {\mathrm f}_{\zeta}=\boldsymbol {\mathrm f}_{s_1} + \boldsymbol {\mathrm f}_{s_2} + \cdots + \boldsymbol {\mathrm f}_{s_j} + \cdots + \boldsymbol {\mathrm f}_{s_T}=\sum_{s_j \in \zeta} \boldsymbol {\mathrm f}_{s_j}
$$
となります。
エキスパートの行動軌跡の尤度$P(\zeta)$は、得られる報酬に指数比例すると考えます。数式で表すと次のようになります。
$$
P(\zeta) \propto \exp R(\zeta)
$$
つまり、ある行動軌跡で得られる報酬が大きいほど、その行動軌跡がエキスパートのものである確率が指数関数的に高くなるということです。
Maximum Entropy IRLでは、$P(\zeta|\theta)$による行動軌跡$\zeta$の特徴量の期待値と、観測した行動軌跡$\zeta$の特徴量の期待値が一致するように、報酬関数を推定します。観測した行動軌跡が$M$個とすると、
$$
\sum_{i=1}^M P(\zeta_i|\theta) \boldsymbol {\rm f}_{\zeta_i} = \frac{1}{M} \sum_{i=1}^M \boldsymbol {\rm f}_{\zeta_i}
$$
となります。$P(\zeta|\theta)$がこの式を満たすように、$\theta$を最適化します。
エキスパートのすべての行動軌跡をサンプルするのは現実的でないので、最大エントロピー原理に従って、観測されなかった行動軌跡の$P(\zeta|\theta)$に対して、一様な確率を割り当てます。最大エントロピー原理による最適な$\theta$は、
$$
\theta^* = {\rm arg~max}_{\theta} \sum_{i=1}^M \log P(\zeta_i|\theta)
$$
と与えられます。この式を次のように変形します(途中計算1)。
$$
\theta^* = {\rm arg~max}_{\theta} \bigg\{ \frac{1}{M} \sum_{i=1}^M \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i} - \log \sum_{i=1}^M \exp \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i} \bigg\}
$$
最適な$\theta$を求めるために、対数尤度$L(\theta)$の勾配を計算します(途中計算2)。
$$
\nabla L(\theta) = \frac{1}{M} \sum_{i=1} \boldsymbol {\rm f}_{s_i} - \sum_{i=1} P(s_i|\theta) \boldsymbol {\rm f}_{s_i}
$$
変形できます。この式は、行動軌跡の特徴量の平均値($\frac{1}{M} \sum_{i=1} \boldsymbol {\rm f}_{s_i}$)と、$P(s_i|\theta)$による行動軌跡の特徴量の期待値を近づけることを意味しています。$\nabla L$がわかったので、勾配法により$\theta$を最適化することができます。よって、報酬関数$R(s_i|\theta)$が求まります。
4. Maximum Entropy IRLの実装
4.1 アルゴリズム
Maximum Entropy IRLで実装するアルゴリズムは以下のようになります。
- 報酬関数$R(s|\theta)$による方策$\pi(s|\theta)$の計算
- 方策$\pi(s|\theta)$による勾配$\nabla L(\theta)$の計算
- $\nabla L(\theta)$によるパラメータ$\theta$の更新
1はValue Iterationの報酬部分を報酬関数$R(s|\theta)$に置き換えることで計算できます。
2の$\nabla L(\theta)$は以下のように計算できました。
$$
\nabla L(\theta) = \frac{1}{M} \sum_{i=1} \boldsymbol {\rm f}_{s_i} - \sum_{i=1} P(s_i|\theta) \boldsymbol {\rm f}_{s_i}
$$
$P(s_i|\theta)$が未知なので、計算をする必要があることがわかります。$P(s_i)$はエキスパートが状態$s_i$を訪れる頻度で、state vistation frequency (SVF)と呼ばれています。
直接$P(s_i)$を求めることはできないので、 あるステップ$t$でエキスパートが状態$s_i$を訪れる頻度$\mu_t(s_i)$を考えます。$P(s_i)$は$\mu_t(s_i)$を使うと、
$$
P(s_i) = \sum_{t=1}^T \mu_t(s_i)
$$
となります。さらに$\mu_t(s)$は次のように計算できます。
$$
\mu_t(s) = \sum_{a \in \cal A} \sum_{s' \in \cal S} \mu_{t-1}(s')\pi(a|s')P(s|a,s')
$$
$\mu_t(s)$はある時点$t$で、エージェントが状態$s$にいる頻度なので、1つ前の時点$t-1$の各状態から状態$s$に遷移する頻度を求め、すべての状態の頻度を足し合わせることで計算されます。$\mu_t(s_i)$が計算できたので、勾配$\nabla L(\theta)$が計算できます。
3のパラメータ$\theta$の更新式は、学習率を$\alpha$とすると
$$
\theta_{\rm new} := \theta_{\rm old} - \alpha \nabla L(\theta)
$$
となります。$\nabla L(\theta)$は計算できたので、学習率を掛けて、パラメータを更新します。
4.2 実装の解説
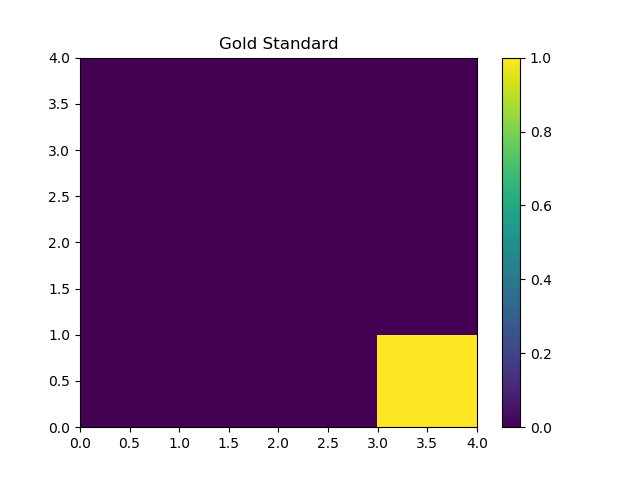
理解しやすくするため、報酬関数が既知でタスクとして簡単なOpenAI GymのFrozenLakeを扱います。求めたい報酬関数は下図のようになります。
Maximum Entropy IRLの実装には、アルゴリズムに対応した3つの処理があります。
- 報酬関数$R(s|\theta)$から方策$\pi(s|\theta)$を計算
- 1の方策$\pi(s|\theta)$から$P(\zeta)$を計算
- 2の$P(\zeta)$から勾配$\nabla L(\theta)$を計算し、$\theta$を更新
1の処理の実装は、次のようになります。
def __call__(self, gamma, epslion, reward_function=None):
probs = self.probs
n_states = self.n_states
n_actions = self.n_actions
V = np.zeros(n_states)
def compute_action_value(state):
A = np.zeros(self.n_actions)
for action in range(n_actions):
for prob, next_state, reward, done in probs[state][action]:
reward = reward if reward_function is None else reward_function(state)
A[action] += prob * (reward + gamma * V[next_state])
return A
while True:
delta = 0
for state in range(n_states):
A = compute_action_value(state)
best_action_value = A.max()
delta = max(delta, np.abs(best_action_value - V[state]))
V[state] = best_action_value
if delta < epslion:
break
policy = np.zeros([n_states, n_actions])
for state in range(n_states):
A = compute_action_value(state)
policy[state] = A
policy -= policy.max(axis=1, keepdims=True)
max_values = np.broadcast_to(policy.max(axis=1, keepdims=True), policy.shape)
policy = np.where(policy == max_values, policy, np.NINF)
policy = np.exp(policy) / np.exp(policy).sum(axis=1, keepdims=True)
return V, policy
- 報酬関数$R(s|\theta)$を受け取り:
$def __call__(self, gamma, epslion, reward_function=None): - 報酬関数$R(s|\theta)$が定義されていれば、報酬関数から報酬を計算:
$reward = reward if reward_function is None else reward_function(state)
これによって、報酬関数$R(s|\theta)$を使って、Value Iterationを実行し、方策$\pi(s|\theta)$を計算できます。
2の処理の実装は、次のようになります。
def __call__(self, policy, trajectories):
n_states = self.n_states
n_actions = self.n_actions
probs = self.probs
n_trajectories, n_steps = trajectories.shape
mu = np.zeros((n_steps, n_states))
for trajectory in trajectories:
mu[0, trajectory[0]] += 1
mu /= n_trajectories
for t in range(1, n_steps):
for action in range(n_actions):
for state in range(n_states):
for prob, next_state, _, _ in probs[state][action]:
mu[t][next_state] += mu[t-1][state] * policy[state][action] * prob
return mu.sum(axis=0)
- 初期化の処理として、
for trajectory in trajectories:のループ内部で、$\mu_0(s_0)$を計算 -
for t in range(1, n_steps):のループで、$\mu_t(s) = \sum_{a \in \cal A} \sum_{s' \in \cal S} \mu_{t-1}(s')\pi(a|s')P(s|a,s')$の計算 -
mu.sum(axis=0)で$P(s_i)$を計算
$P(s_i)$を計算することができました。
3の処理の実装は、次のようになります。
for i in range(n_epochs):
V, policy = value_iteration(gamma, epsilon, reward_function)
mu = svf(policy, trajectories)
grad = experts_feature - feature_matrix.T.dot(mu)
reward_function.update(learning_rate * grad)
1.報酬関数から方策を計算:V, policy = value_iteration(gamma, epsilon, reward_function)
2. 方策から$P(\zeta)$を計算: mu = svf(policy, trajectories)
3. 勾配を計算: grad = experts_feature - feature_matrix.T.dot(mu)
4. 報酬関数のパラメータを更新: reward_function.update(learning_rate * grad)
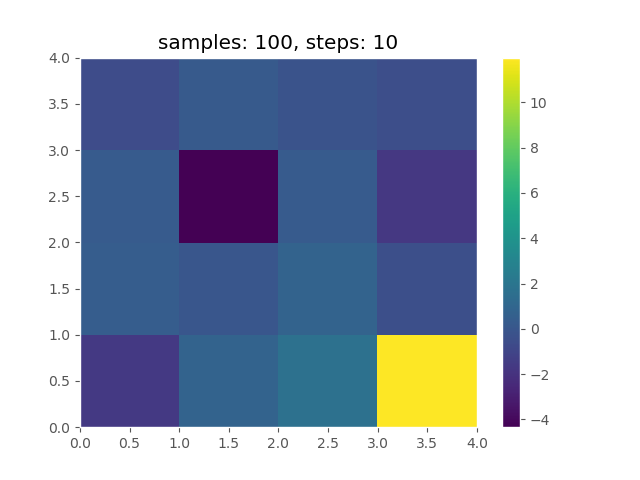
コードを実行して、報酬関数を求めると以下のようになります。
おおよそ正しく復元できていることがわかります。
参考
論文 & Webページ
- 海鳥の経路予測のための逆強化学習
- Maximum Entropy Inverse Reinforcement Learning (Original Paper)
- Inverse Reinforcement Learning pt. I
- Revisit Maximum Entropy Inverse Reinforcement Learning
- Modeling Purposeful Adaptive Behavior with the Principle of Maximum Causal Entropy
実装
補足1
$$
\begin{eqnarray}
\theta^* &=& {\rm arg~max}_{\theta} \sum_{i=1}^M \log P(\zeta_i|\theta) \
&=& {\rm arg~max}_{\theta} \frac{1}{M} \sum_{i=1}^M \log
P(\zeta_i|\theta) \
&=& {\rm arg~max}_{\theta} \frac{1}{M} \sum_{i=1}^M \log
\frac{\exp R(\zeta_i)}{Z} \
&=& {\rm arg~max}_{\theta} \bigg\{ \frac{1}{M} \sum_{i=1}^M R(\zeta_i) - \log Z \bigg\}
\end{eqnarray}
$$
ここで$Z$は分配関数であるので、$Z=\sum_{i=1}^M \exp R(\zeta_i)$となります。この式を代入すると、
$$
\begin{eqnarray}
\theta^* &=& {\rm arg~max}_{\theta} \bigg\{ \frac{1}{M} \sum_{i=1}^M R(\zeta_i) - \log \sum_{i=1}^M \exp R(\zeta_i) \bigg\} \
&=& {\rm arg~max}_{\theta} \bigg\{ \frac{1}{M} \sum_{i=1}^M \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i} - \log \sum_{i=1}^M \exp \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i} \bigg\}
\end{eqnarray}
$$
補足2
$$
\begin{eqnarray}
\nabla L(\theta) &=& \frac{\partial}{\partial \theta} \bigg\{ \frac{1}{M} \sum_{i=1}^M \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i} - \log \sum_{i=1}^M \exp \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i} \bigg\} \
&=& \frac{1}{M}\sum_{i=1}^M \boldsymbol {\rm f}_{\zeta_i} - \frac{1}{\sum_{i=1}^M \exp \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i}} \frac{\partial}{\partial \theta} \sum_{i=1}^M \exp \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i} \
&=& \frac{1}{M}\sum_{i=1}^M \boldsymbol {\rm f}_{\zeta_i} - \sum_{i=1}^M \frac{\exp \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_i}}{\sum_{j=1}^M \exp \theta^{\rm T} \boldsymbol {\rm f}_{\zeta_j}} \boldsymbol {\rm f}_{\zeta_i} \
&=& \frac{1}{M} \sum_{i=1}^M \boldsymbol {\rm f}_{\zeta_i} - \sum_{i=1}^M P(\zeta_i|\theta) \boldsymbol {\rm f}_{\zeta_i}
\end{eqnarray}
$$
行動軌跡は、エキスパートの行動した状態列なので、
$$
\nabla L(\theta) = \frac{1}{M} \sum_{i=1} \boldsymbol {\rm f}_{s_i} - \sum_{i=1} P(s_i|\theta) \boldsymbol {\rm f}_{s_i}
$$