OpenCVでスプライトを半透明にする #1 ～おばけを出現させる～

はじめに

あるアプリを作っている中で画像の加工が必要となった。
加工自体はそれほど苦労せずにできたが、あとになって考えるとそれは以前悩みに悩み、結局できなかった難題だった。
それがいつの間にかできるようになっていたとは。これは記録に残さねば。自分のために。

目次

OpenCVでスプライトを半透明にする #1　～おばけを出現させる～　←今ここ
OpenCVでスプライトを半透明にする #2　～グラデーションな半透明を作る～

関連記事

OpenCVで透過画像を扱う　～スプライトを舞わせる～
OpenCVでスプライトを回転させる
OpenCVでスプライトを回転させる #2　～cv2.warpAffine()を使いこなす～
OpenCVでスプライトを回転させる #3　～人任せにせず自分で計算せよ～

復習と予習

numpy配列の計算

numpyではスカラーと配列（行列）という次元の異なるものに対してうまい具合に次元変換して演算をしてくれる。これをブロードキャストという。
変数だとスカラーと行列の違いがわかりづらいのでここでは行列の計算として例を示す。
「自分で違いがわかるような変数の名付け方をすればいいじゃないか」ですって？ それはごもっとも。

スカラーと行列の加減算

スカラーと行列の加減算ではスカラーは全要素がその値の行列として扱われる。
数学では全要素が1の行列に特に記号は与えられていないんですかね。単位行列のIやEみたいな感じで。

\begin{align} 
k + A &= 
\begin{pmatrix}
k & k \\
k & k \\
\end{pmatrix}
 + \begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{pmatrix} \\
&= \begin{pmatrix}
k + a_{11} & k + a_{11}  \\
k + a_{21} & k + a_{22}  \\
\end{pmatrix}
\end{align}

行列の要素ごとの乗算（アダマール積）

行列の要素ごとの積をアダマール積というが、numpyではA*Bと乗算記号*を使う。

\begin{align} 
A \otimes B &= 
\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{pmatrix}
 \otimes
\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22} \\
\end{pmatrix} \\
&= \begin{pmatrix}
a_{11}b_{11} & a_{12}b_{12}  \\
a_{21}b_{21} & a_{22}b_{22}  \\
\end{pmatrix}
\end{align}

スカラーと行列の乗算

スカラーと行列の乗算は普通に行列の各要素をスカラー倍する。
numpyでは当然、k*Aと乗算記号*を使う。
アダマール積の演算子が*であることに違和感があったが、このスカラー倍はスカラーを行列にブロードキャストして行列同士でアダマール積を計算していると解釈することができる。だから*で問題ない。

\begin{align} 
kA &= 
 \begin{pmatrix}
ka_{11} & ka_{12} \\
ka_{21} & ka_{22} \\
\end{pmatrix}
\end{align}

ビット演算

bitwise_and() / bitwise_or()

行列の各要素について ビット演算 をする。

ある値、たとえば 89 rgb(89,0,0) について、輝度0 rgb(0,0,0) と輝度255 rgb(255,0,0) 、さらに中途半端な数値203 rgb(203,0,0) とのbitwise_andとbitwise_orを取ってみる。

	0 rgb(0,0,0)	255 rgb(255,0,0)	203 rgb(203,0,0)
bitwise_and	89 : 0b01011001 and 0 : 0b00000000 = 0 : 0b00000000 rgb(0,0,0)	89 : 0b01011001 and 255 : 0b11111111 = 89 : 0b01011001 rgb(89,0,0)	89 : 0b01011001 and 203 : 0b11001011 = 73 : 0b01001001 rgb(73,0,0)
bitwise_or	89 : 0b01011001 or 0 : 0b00000000 = 89 : 0b01011001 rgb(89,0,0)	89 : 0b01011001 or 255 : 0b11111111 = 255 : 0b11111111 rgb(255,0,0)	89 : 0b01011001 or 203 : 0b11001011 = 219 : 0b11011011 rgb(219,0,0)

これが以前の記事で書いた
　　x(任意の色) and 255(白) = x(任意の色)
　　x(任意の色) and 0(黒) = 0(黒)
　　x(任意の色) or 255(白) = 255(白)
　　x(任意の色) or 0(黒) = x(任意の色)
というマスクの詳細だ。
さらに、0と255以外の値でビット演算すると想定外の値が出てきてしまうことも示している。

bitwise_and / bitwise_orはOpenCVだけでなくnumpyにもあり、基本的には同じだが細かいところで微妙に違うので注意が必要だ。

# スカラー値のビット演算　numpy
print(np.bitwise_and(6, 5))
4       # スカラーが返った

# スカラー値のビット演算　cv2
print(cv2.bitwise_and(6, 5))
[[4.]
 [0.]
 [0.]
 [0.]]
# ↑ float64の2次元numpy配列が返った


# スカラーとリストのビット演算　numpy
print(np.bitwise_and(6, [5]))
[4]     # リストが返った　ブロードキャストしてくれたのだろう

# スカラーとリストのビット演算　cv2
print(cv2.bitwise_and(6, [5])) 
# 使えるのはスカラーかnumpy配列に限られるのでエラー

重み付きの合成

cv2.addWeighted()

OpenCVではcv2.addWeighted()で二つの画像を重みを指定して合成することができる。
もちろん二つの画像はサイズおよびチャンネル数が同一である必要がある。

dst = cv2.addWeighted(src1, alpha, src2, beta, gamma)

• src1, src2　　画像。行列
• appha, beta　重み。スカラー値
• gamma　　　各計算結果に足されるスカラー値

これで dst = alpha * src1 + beta * src2 + gamma という結果が得られる。
行列で書けば

\begin{align} 
\alpha A + \beta B + \gamma &= 
\alpha \begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{pmatrix}
 + \beta\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22} \\
\end{pmatrix}
 + \gamma\begin{pmatrix}
1 & 1 \\
1 & 1 \\
\end{pmatrix} \\
&= \begin{pmatrix}
\alpha a_{11} + \beta b_{11} + \gamma & \alpha a_{12} + \beta b_{12} + \gamma \\
\alpha a_{21} + \beta b_{21} + \gamma & \alpha a_{22} + \beta b_{22} + \gamma \\
\end{pmatrix}
\end{align}

ということ。行列のスカラー倍および行列同士の和を計算しているだけだからnumpyでもできなくはないが、この関数のほうがnumpyより約2倍速いらしい。

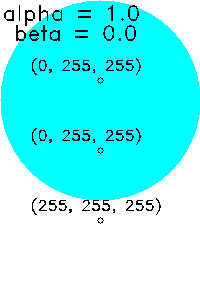
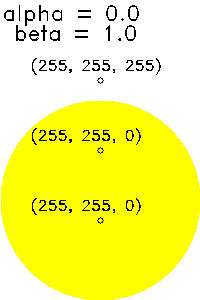
(α, β)=(1.0, 0.0)		(α, β)=(0.0, 1.0)
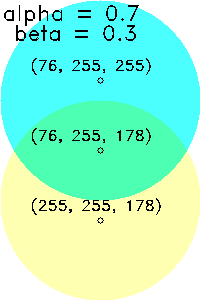
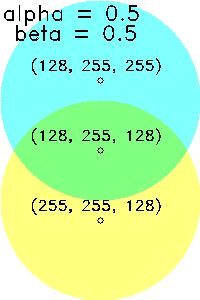
(α, β)=(0.7, 0.3)	(α, β)=(0.5, 0.5)	(α, β)=(0.2, 0.8)

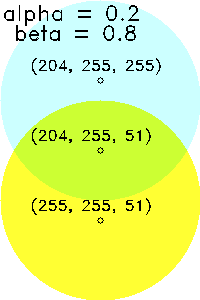alpha と beta は合計が1となるようにするのが普通だ。1でなくてもエラーにはならないが、計算を理解していれば結果は推測できる。全体的に暗くなったり明るくなったりしてしまうのだ。
gammaを有効的に利用している例は見たことがない。
行列がnp.uint8のnumpy配列の場合、計算により0～255の範囲を超えてしまったときは0や255に収まるように調整される。

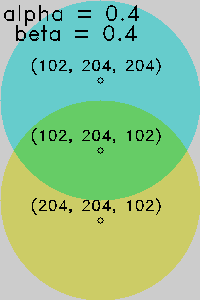
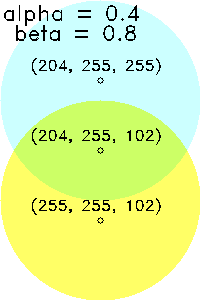
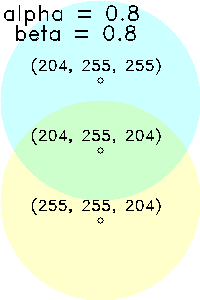
(α, β)=(0.4, 0.4) 計0.8	(α, β)=(0.4, 0.8) 計1.2	(α, β)=(0.8, 0.8) 計1.6

半透明スプライトへの挑戦

ここからが本番。
cv2.addWeighted()を使って半透明スプライトを実装することはできないだろうか。

いらすとやの「ハロウィンのキャラクター（おばけ）」（を縮小したもの）で考えてみよう。背景は「ハロウィンの背景素材（オレンジ）」の一部を前景と同じサイズにトリミングしたもの。

前景 RGBA画像	背景（の一部） RGB画像	→	期待する結果
		→

RGBAとして合成してみる

RGBA画像とRGB画像を合成することはできないので、cv2.cvtColor()で背景を全体的に不透明なRGBA画像に変換してからalpha=0.5, beta=0.5で合成してみる。

前景 RGBA画像	背景 RGBAに変換	→	合成結果 RGBA画像
		→

合成はできたが、RGBAのA要素まで合成されているので、右上のピクセルは
　0.5 * rgba(0,0,0,0) + 0.5 * rgba(239,130,0,255) = rgba(120,65,0,128)
となってしまっている。
この透過画像をあらためてRGBに変換したところで rgba(120,65,0,128) が rgb(120,65,0) になるだけで、背景のオレンジ色 rgb(239,130,0) が保持されるわけではない。

RGBとして合成してみる

次に前景画像をRGBにして合成してみる。透明な部分rgba(0,0,0,0)のA要素を除くとrgb(0,0,0) になるので、透明部分は黒として表示される。
結果はRGBAを合成してからRGBに変換したものと同じだ。

前景 RGBに変換	背景 RGB画像	→	合成結果 RGB画像
		→

一部のみ半透明にする

前景画像の不透明な部分は背景と合成して半透明にし、前景画像の透明な部分は背景のみとする。そんな都合のよい関数は存在しないので自分で作る必要がある。
どうやって？
どうやってって、今自分で書いただろ、仕様を。その通りにやればいいんだよ。
肝は、スプライト関数の記事でも使ったマスク処理にある。

合成した部分のみを切り出す

さっき作った全体を合成した画像（前景の黒地も合成されてしまっている）にマスク処理をおこなって必要な合成部分を取り出す。
これで前景画像の不透明な部分は背景と合成して半透明で背景部分が黒な画像ができる。

全体を合成	前景を残し 背景を消すマスク	→	前景部分は合成 背景部分は黒
		→

背景のみを切り出す

それとは別に前景画像の透明な部分は背景のみで前景画像の不透明な部分は黒の画像を作る。

背景のみ	前景を消し 背景を残すマスク	→	前景部分は黒 背景部分はそのまま
		→

両者を合体する

そして二つの中間画像を合体すれば求める画像を作ることができる。
ここで言う合体は重みのある合成ではない。alpha=1かつbeta=1での合成といえなくもないが、とにかく単なる足し算だ。背景部分と前景部分の少なくともどちらかが rgb(0,0,0)なので、わざわざcv2.addWeighted()を使わずとも255を超えて変な色になってしまうことはない。

前景部分は合成 背景部分は黒	前景部分は黒 背景部分はそのまま	→	完成形
		→

ソース

スプライト関数の記事では背景画像からはみ出したときの処理が最初から実装されておりやや読みづらかったので、ここでは最小限のコードを示す。

sprite_alpha.py

import cv2

def sprite_alpha(back, front4, alpha):
    front = front4[:, :, :3]                        # RGB（3ch）
    mask = front4[:, :, 3]                          # A要素（1ch）
    mask = cv2.merge((mask, mask, mask))            # 3chにする

    # 全体を合成
    compo = cv2.addWeighted(front, alpha, back, 1-alpha, 0)
    # マスク処理
    compo_with_mask = cv2.bitwise_and(compo, mask)
    back_with_mask = cv2.bitwise_and(back, 255-mask)

    # 必要に応じて有効化してください
    # cv2.imshow("compo", compo)
    # cv2.imshow("mask", mask)
    # cv2.imshow("255-mask", 255-mask)
    # cv2.imshow("compo_with_mask", compo_with_mask)
    # cv2.imshow("back_with_mask", back_with_mask)

    # 完成形
    result = compo_with_mask + back_with_mask
    return result

def main():
    front_RGBA = cv2.imread("ghost.png", -1)        # 前景　RGBA画像
    back_origin = cv2.imread("background.png")      # 背景　RGB画像
    height, width = front_RGBA.shape[:2]            # 前景のサイズ
    x, y = 200, 200                                 # トリミング左上座標
    back = back_origin[y:y+height, x:x+width]       # 背景をトリミング
    alpha = 0.5                                     # アルファ値
    image = sprite_alpha(back, front_RGBA, alpha)
    cv2.imshow("image", image)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

if __name__ == "__main__":
    main()

255-maskが不自然と感じる人がいるかもしれないが、すでに説明している。

\begin{align} 
255 - A &= 
 \begin{pmatrix}
255 & 255 \\
255 & 255 \\
\end{pmatrix}
 - \begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{pmatrix}
 \\
&= \begin{pmatrix}
255-a_{11} & 255-a_{12} \\
255-a_{21} & 255-a_{22} \\
\end{pmatrix}
\end{align}

で、もとの行列をネガポジ反転しているわけだ。

現段階ではスプライトとしては甚だ不十分で、最初の大きな背景から前景がはみ出すような座標を設定するとエラーになってしまうし、そもそも大きな背景の上に前景を合成する仕様にはなっていない。
しばらくはこのかたちでお付き合いください。

ギャラリー

アルファ値を変更すればさまざまな半透明を作ることができる。ソースは略。

現れたり消えたり

終わりに

今回、行列にこだわって記事を書いた。それは自分の理解を深めるためと、OpenCVの関数を使わず行列の計算で対応できないか試してみたかったため。
そして今回の半透明処理は大きく汎用化できることに気づいたのであった。

つづく