LoginSignup
4
3

More than 5 years have passed since last update.

@mckeeeen(mckeeeen)

【第2章】pythonで「経済・ファイナンスデータの計量時系列分析」の章末問題を解く

Last updated at Posted at 2018-02-11

自分の勉強用に、沖本竜義「経済・ファイナンスデータの計量経済分析」の章末問題をpythonで解いてみました。
jupyter notebook上で記述したものをほぼそのまま載せてあります。
ソースコードの細かい説明は省いてありますが、今後余裕があれば説明を加えようと思います。

こちらの記事は第2章の章末問題を解いたものになります。
第1章、第4章、第5章、第6章、第7章も公開しています。

各種設定・モジュールのインポート

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import chi2
from statsmodels.tsa.stattools import acf
from statsmodels.tsa.stattools import pacf
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.arima_model import ARMA

import matplotlib as mpl
font = {"family":"IPAexGothic"}
mpl.rc('font', **font)
plt.rcParams["font.size"] = 12

2.5

(1)

ファイルをインポートする

eco = pd.read_csv('./input/economicdata.csv')
print(eco.shape)
eco.head()

(364, 7)
date topix exrate indprod cpi saunemp intrate
0 Jan-75 276.09 29.13 47.33 52.625 1.7 12.67
1 Feb-75 299.81 29.70 46.86 52.723 1.8 13.00
2 Mar-75 313.50 29.98 46.24 53.114 1.8 12.92
3 Apr-75 320.57 29.80 47.33 54.092 1.8 12.02
4 May-75 329.65 29.79 47.33 54.385 1.8 11.06

対数差分系列を計算する

eco['indprod_dlog'] = np.log(eco.indprod).diff()
eco.head()
date topix exrate indprod cpi saunemp intrate indprod_dlog
0 Jan-75 276.09 29.13 47.33 52.625 1.7 12.67 NaN
1 Feb-75 299.81 29.70 46.86 52.723 1.8 13.00 -0.009980
2 Mar-75 313.50 29.98 46.24 53.114 1.8 12.92 -0.013319
3 Apr-75 320.57 29.80 47.33 54.092 1.8 12.02 0.023299
4 May-75 329.65 29.79 47.33 54.385 1.8 11.06 0.000000

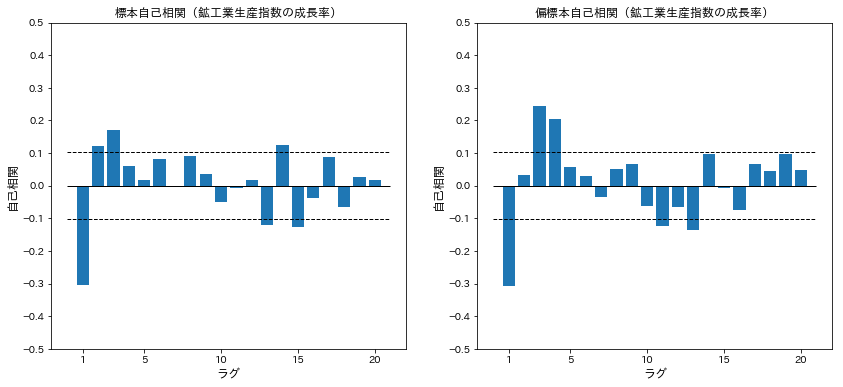
標本自己相関関数と標本偏自己相関関数を計算する
ただし、標本偏自己相関関数はOLS係数推定量として求める（教科書に沿った形です）

acf_ind=acf(eco.indprod_dlog[1:]) 
pacf_ind=pacf(eco.indprod_dlog[1:],method='ols') 
lag=range(41)

プロットする

y=[acf_ind,pacf_ind]
fig,ax=plt.subplots(1,2,figsize=[14,6])
for i in range(2):   
    ax[i].bar(lag[1:21],y[i][1:21])
    ax[i].set_ylim(-0.5,0.5)
    ax[i].set_xticks([1,5,10,15,20])
    ax[i].set_yticks(np.asarray(range(-5,6))*0.1)
    ax[i].hlines(0,0,21,linewidth=1)
    ax[i].hlines([1.96/np.sqrt(eco.shape[0]-1),-1.96/np.sqrt(eco.shape[0]-1)],0,21,linestyles='dashed',linewidth=1)
    ax[i].set_xlabel('ラグ',fontsize=12)
    ax[i].set_ylabel('自己相関',fontsize=12)
ax[0].set_title('標本自己相関（鉱工業生産指数の成長率）')
ax[1].set_title('偏標本自己相関（鉱工業生産指数の成長率）')

plt.show()

output_10_0.png

AR(4),MA(3),ARMA(1,1),ARMA(2,1),ARMA(1,2),ARMA(2,2)でモデル化する
ただし、statsmodelsにはMAモデルのクラスが見当たらなかったのでARMAモデルのAR成分を0にすることで対応
今回は、ARモデルもARMAモデルのMA成分を0にすることで対応してみる
参考: http://www.blackarbs.com/blog/time-series-analysis-in-python-linear-models-to-garch/11/1/2016#AR

ar_4=ARMA(eco.indprod_dlog[1:].values,[4,0]).fit()
ma_3=ARMA(eco.indprod_dlog[1:].values,[0,3]).fit()
arma_1_1=ARMA(eco.indprod_dlog[1:].values,[1,1]).fit()
arma_2_1=ARMA(eco.indprod_dlog[1:].values,[2,1]).fit()
arma_1_2=ARMA(eco.indprod_dlog[1:].values,[1,2]).fit()
arma_2_2=ARMA(eco.indprod_dlog[1:].values,[2,2]).fit()

各モデルのAIC,SICを計算する
教科書の値と異なる値となったが、選択されるモデルは同じ

model=[ar_4,ma_3,arma_1_1,arma_2_1,arma_1_2,arma_2_2]
aic=[]
sic=[]
T=eco.indprod_dlog[1:].shape[0]
for i in range(len(model)):
    aic.append(model[i].aic/T)
    sic.append(model[i].bic/T)
model_sel=pd.DataFrame({'AIC':aic,'SIC':sic},index=['AR(4)','MA(3)','ARMA(1,1)','ARMA(2,1)','ARMA(1,2)','ARMA(2,2)'])
model_sel.T
AR(4) MA(3) ARMA(1,1) ARMA(2,1) ARMA(1,2) ARMA(2,2)
AIC -5.969405 -5.961817 -5.876225 -5.923565 -5.968149 -5.954818
SIC -5.905035 -5.908175 -5.833311 -5.869923 -5.914507 -5.890448

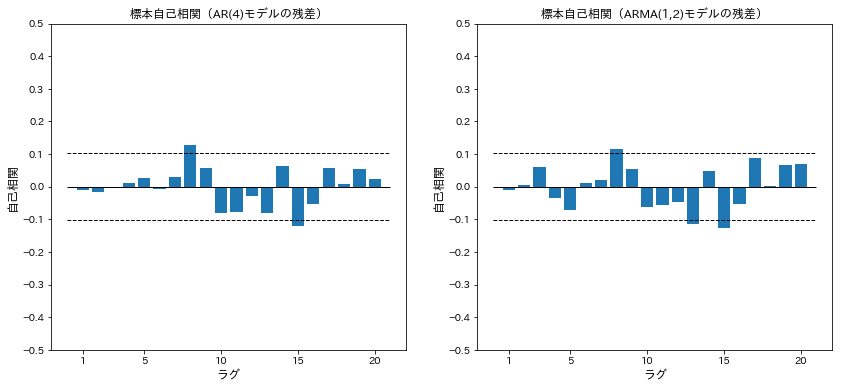
AR(4)モデルとARMA(1,2)モデルの残差を計算し、標本自己相関関数を計算する

acf_ar_4=acf(ar_4.resid)
acf_arma_1_2=acf(arma_1_2.resid)

プロットする

y=[acf_ar_4,acf_arma_1_2]
fig,ax=plt.subplots(1,2,figsize=[14,6])
for i in range(2):   
    ax[i].bar(lag[1:21],y[i][1:21])
    ax[i].set_ylim(-0.5,0.5)
    ax[i].set_xticks([1,5,10,15,20])
    ax[i].set_yticks(np.asarray(range(-5,6))*0.1)
    ax[i].hlines(0,0,21,linewidth=1)
    ax[i].set_xlabel('ラグ',fontsize=12)
    ax[i].set_ylabel('自己相関',fontsize=12)
ax[0].hlines([1.96/np.sqrt(ar_4.resid.shape[0]),-1.96/np.sqrt(ar_4.resid.shape[0])],0,21,linestyles='dashed',linewidth=1)
ax[1].hlines([1.96/np.sqrt(arma_1_2.resid.shape[0]),-1.96/np.sqrt(arma_1_2.resid.shape[0])],0,21,linestyles='dashed',linewidth=1)
ax[0].set_title('標本自己相関（AR(4)モデルの残差）')
ax[1].set_title('標本自己相関（ARMA(1,2)モデルの残差）')

plt.show()

output_18_0.png

(2)

AR(4)モデルの残差について自己相関検定を行う

Q(m)やP値が教科書と異なるのは、学習に用いたmethodが異なるからだと考えられる（残差も正確には教科書と異なっている）

結果、AR(4)モデルの残差が自己相関を持つとは言えない（適切なモデルであると言える）

q_m_ar_4=acorr_ljungbox(ar_4.resid)[0]
p_value_ar_4=chi2.sf(q_m_ar_4,6)
lag=range(1,41)
test_ar_4=pd.DataFrame({'lag':lag,'autocorr':acf_ar_4[1:],'Q(m)':q_m_ar_4,'P_value':p_value_ar_4})
test_ar_4[['lag','autocorr','Q(m)','P_value']].iloc[0:10,:].T
0 1 2 3 4 5 6 7 8 9
lag 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000
autocorr -0.009783 -0.017589 -0.004028 0.012414 0.027854 -0.007964 0.031076 0.127591 0.058008 -0.080286
Q(m) 0.035029 0.148575 0.154546 0.211425 0.498562 0.522104 0.881525 6.957480 8.216885 10.636289
P_value 0.999999 0.999935 0.999927 0.999818 0.997856 0.997559 0.989708 0.324797 0.222641 0.100289

ARMA(1,2)モデルの残差について自己相関検定を行う
Q(m)やP値が教科書と異なるのは、学習に用いたmethodが異なるからだと考えられる（残差も正確には教科書と異なっている）
結果、AR(4)モデルの残差が自己相関を持つとは言えない（適切なモデルであると言える）

q_m_arma_1_2=acorr_ljungbox(arma_1_2.resid)[0]
p_value_arma_1_2=chi2.sf(q_m_arma_1_2,7)
lag=range(1,41)
test_arma_1_2=pd.DataFrame({'lag':lag,'autocorr':acf_arma_1_2[1:],'Q(m)':q_m_arma_1_2,'P_value':p_value_arma_1_2})
test_arma_1_2[['lag','autocorr','Q(m)','P_value']].iloc[0:10,:].T
0 1 2 3 4 5 6 7 8 9
lag 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000
autocorr -0.011002 0.005265 0.060629 -0.034401 -0.070794 0.010740 0.020772 0.116308 0.054963 -0.062463
Q(m) 0.044306 0.054481 1.407365 1.844126 3.698984 3.741790 3.902374 8.951175 10.081840 11.546259
P_value 1.000000 1.000000 0.985345 0.967962 0.813722 0.808991 0.790951 0.256181 0.183983 0.116503

2.6

(1)

ファイルをインポートする

arma = pd.read_csv('./input/arma.csv')
print(arma.shape)
arma.head()

(300, 3)
y1 y2 y3
0 -0.091682 0.104645 -1.350264
1 0.533702 1.253242 -0.324967
2 -0.501343 0.189352 0.291934
3 0.486156 -0.189821 -1.472085
4 0.489030 0.451640 -1.335709

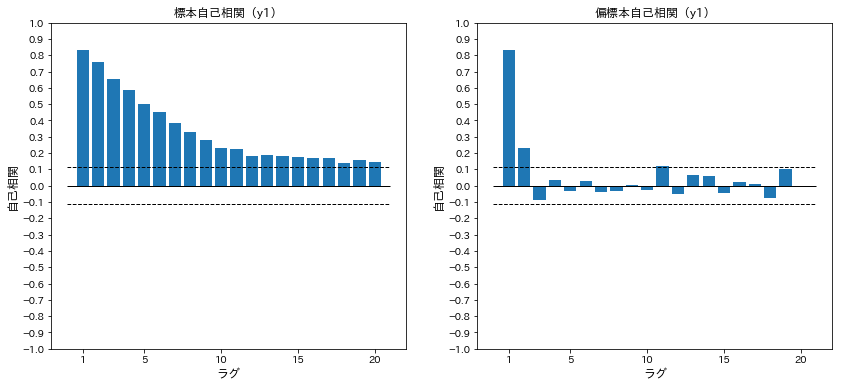
y1の標本自己相関関数と標本偏自己相関関数を計算する

acf_y1=acf(arma.y1)
pacf_y1=pacf(arma.y1)

プロットする

y=[acf_y1,pacf_y1]
fig,ax=plt.subplots(1,2,figsize=[14,6])
for i in range(2):   
    ax[i].bar(range(1,21),y[i][1:21])
    ax[i].set_ylim(-1,1)
    ax[i].set_xticks([1,5,10,15,20])
    ax[i].set_yticks(np.asarray(range(-10,11))*0.1)
    ax[i].hlines(0,0,21,linewidth=1)
    ax[i].hlines([1.96/np.sqrt(arma.shape[0]),-1.96/np.sqrt(arma.shape[0])],0,21,linestyles='dashed',linewidth=1)
    ax[i].set_xlabel('ラグ',fontsize=12)
    ax[i].set_ylabel('自己相関',fontsize=12)
ax[0].set_title('標本自己相関（y1）')
ax[1].set_title('偏標本自己相関（y1）')

plt.show()

output_30_0.png

(2)

上記プロットの結果から、AR(2)が最有力で、ARMAの可能性もある
AR(2)、ARMA(1,1)、ARMA(2,1)、ARMA(1,2)をモデル候補とする（ARMA(2,2)は定常性の過程が成り立たないとして却下された）

ar_2=ARMA(arma.y1.values,[2,0]).fit()
arma_1_1=ARMA(arma.y1.values,[1,1]).fit()
arma_2_1=ARMA(arma.y1.values,[2,1]).fit()
arma_1_2=ARMA(arma.y1.values,[1,2]).fit()
# arma_2_2=ARMA(arma.y1.values,[2,2]).fit()

model=[ar_2,arma_1_1,arma_2_1,arma_1_2]
aic=[]
sic=[]
T=eco.indprod_dlog[1:].shape[0]
for i in range(len(model)):
    aic.append(model[i].aic/T)
    sic.append(model[i].bic/T)
model_sel=pd.DataFrame({'AIC':aic,'SIC':sic},index=['AR(2)','ARMA(1,1)','ARMA(2,1)','ARMA(1,2)'])
model_sel.T
AR(2) ARMA(1,1) ARMA(2,1) ARMA(1,2)
AIC 2.499130 2.507680 2.497055 2.503431
SIC 2.539943 2.548493 2.548072 2.554448

(4)

AICではARMA(2,1)、SICではAR(2)が選択される

まず、ARMA(2,1)モデルの残差について自己相関検定を行う（ただし、m=10とする）

結果、ARMA(2,1)モデルの残差が自己相関を持つとは言えない（適切なモデルであると言える）

q_m_arma_2_1=acorr_ljungbox(arma_2_1.resid)[0]
p_value_arma_2_1=chi2.sf(q_m_arma_2_1,7)
lag=range(1,41)
test_arma_2_1=pd.DataFrame({'lag':lag,'autocorr':acf_y1[1:],'Q(m)':q_m_arma_2_1,'P_value':p_value_arma_2_1})
test_arma_2_1[['lag','autocorr','Q(m)','P_value']].iloc[0:10,:].T
0 1 2 3 4 5 6 7 8 9
lag 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000
autocorr 0.830991 0.761174 0.652177 0.584840 0.503205 0.450812 0.383598 0.328185 0.278296 0.229232
Q(m) 0.002502 0.036143 0.112850 0.128471 0.190753 0.915685 0.920768 0.941598 1.040412 3.827893
P_value 1.000000 1.000000 0.999996 0.999995 0.999979 0.996076 0.996007 0.995716 0.994150 0.799374

次に、AR(2)モデルの残差について自己相関検定を行う（ただし、m=10とする）

結果、AR(2)モデルの残差が自己相関を持つとは言えない（適切なモデルであると言える）

q_m_ar_2=acorr_ljungbox(ar_2.resid)[0]
p_value_ar_2=chi2.sf(q_m_ar_2,8)
lag=range(1,41)
test_ar_2=pd.DataFrame({'lag':lag,'autocorr':acf_y1[1:],'Q(m)':q_m_ar_2,'P_value':p_value_ar_2})
test_ar_2[['lag','autocorr','Q(m)','P_value']].iloc[0:10,:].T
0 1 2 3 4 5 6 7 8 9
lag 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000
autocorr 0.830991 0.761174 0.652177 0.584840 0.503205 0.450812 0.383598 0.328185 0.278296 0.229232
Q(m) 0.138707 1.082496 2.001496 2.244934 2.769646 3.477106 3.482886 3.487488 3.695579 6.845535
P_value 0.999999 0.997672 0.980966 0.972567 0.947971 0.900959 0.900514 0.900159 0.883492 0.553386

(5)

まず、y2に関して同様の分析を行う

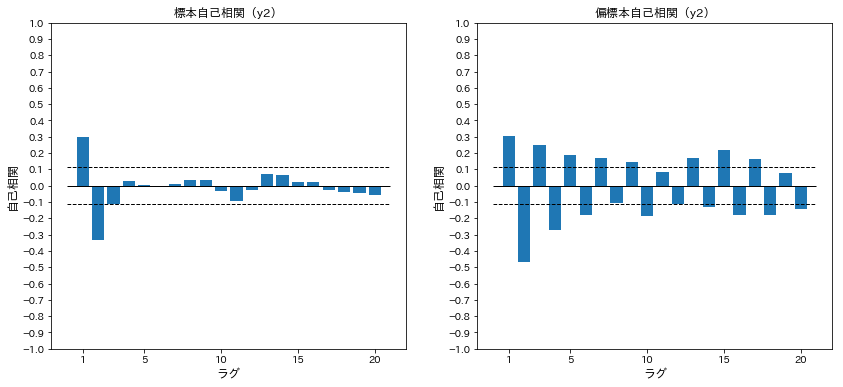
y2の標本自己相関関数と標本偏自己相関関数を計算する

acf_y2=acf(arma.y2)
pacf_y2=pacf(arma.y2)

プロットする

y=[acf_y2,pacf_y2]
fig,ax=plt.subplots(1,2,figsize=[14,6])
for i in range(2):   
    ax[i].bar(range(1,21),y[i][1:21])
    ax[i].set_ylim(-1,1)
    ax[i].set_xticks([1,5,10,15,20])
    ax[i].set_yticks(np.asarray(range(-10,11))*0.1)
    ax[i].hlines(0,0,21,linewidth=1)
    ax[i].hlines([1.96/np.sqrt(arma.shape[0]),-1.96/np.sqrt(arma.shape[0])],0,21,linestyles='dashed',linewidth=1)
    ax[i].set_xlabel('ラグ',fontsize=12)
    ax[i].set_ylabel('自己相関',fontsize=12)
ax[0].set_title('標本自己相関（y2）')
ax[1].set_title('偏標本自己相関（y2）')

plt.show()

output_45_0.png

上記プロットの結果から、MA(2)、MA(3)が有力で、ARMAの可能性もある
季節性が残っているようにも見える
MA(2)、ARMA(2,1)、ARMA(2,2)、ARMA(2,3)、ARMA(3,1)、ARMA(3,2)、ARMA(3,3)をモデル候補とする（MA(3)、ARMA(1,1)、ARMA(1,2)、ARMA(1,3)は定常性の過程が成り立たないとして却下された）

ma_2=ARMA(arma.y2.values,[0,2]).fit()
# ma_3=ARMA(arma.y2.values,[0,3]).fit()
# arma_1_1=ARMA(arma.y2.values,[1,1]).fit()
# arma_1_2=ARMA(arma.y2.values,[1,2]).fit()
# arma_1_3=ARMA(arma.y2.values,[1,3]).fit()
arma_2_1=ARMA(arma.y2.values,[2,1]).fit()
arma_2_2=ARMA(arma.y2.values,[2,2]).fit()
arma_2_3=ARMA(arma.y2.values,[2,3]).fit()
arma_3_1=ARMA(arma.y2.values,[3,1]).fit()
arma_3_2=ARMA(arma.y2.values,[3,2]).fit()
arma_3_3=ARMA(arma.y2.values,[3,3]).fit()

model=[ma_2,arma_2_1,arma_2_2,arma_2_3,arma_3_1,arma_3_2,arma_3_3]
aic=[]
sic=[]
T=eco.indprod_dlog[1:].shape[0]
for i in range(len(model)):
    aic.append(model[i].aic/T)
    sic.append(model[i].bic/T)
model_sel=pd.DataFrame({'AIC':aic,'SIC':sic},index=['MA(2)','ARMA(2,1)','ARMA(2,2)','ARMA(2,3)','ARMA(3,1)','ARMA(3,2)','ARMA(3,3)'])
model_sel.T
MA(2) ARMA(2,1) ARMA(2,2) ARMA(2,3) ARMA(3,1) ARMA(3,2) ARMA(3,3)
AIC 2.356034 2.293800 2.298995 2.296927 2.29918 2.302264 2.302285
SIC 2.396847 2.344816 2.360215 2.368350 2.36040 2.373687 2.383911

AICとSICどちらでもARMA(2,1)が選択される
ARMA(2,1)モデルの残差について自己相関検定を行う（ただし、m=10とする）

結果、ARMA(2,1)モデルの残差が自己相関を持つとは言えない（適切なモデルであると言える）

q_m_arma_2_1=acorr_ljungbox(arma_2_1.resid)[0]
p_value_arma_2_1=chi2.sf(q_m_arma_2_1,7)
lag=range(1,41)
test_arma_2_1=pd.DataFrame({'lag':lag,'autocorr':acf_y2[1:],'Q(m)':q_m_arma_2_1,'P_value':p_value_arma_2_1})
test_arma_2_1[['lag','autocorr','Q(m)','P_value']].iloc[0:10,:].T
0 1 2 3 4 5 6 7 8 9
lag 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000
autocorr 0.301309 -0.330950 -0.110256 0.026641 0.001279 -0.001494 0.013197 0.035491 0.036527 -0.034517
Q(m) 0.000551 0.236224 0.296538 2.742206 2.891474 2.917825 3.211499 3.232176 3.393568 3.562742
P_value 1.000000 0.999956 0.999904 0.907783 0.894857 0.892499 0.864772 0.862726 0.846367 0.828536

y3の標本自己相関関数と標本偏自己相関関数を計算する

acf_y3=acf(arma.y3)
pacf_y3=pacf(arma.y3)

プロットする

y=[acf_y3,pacf_y3]
fig,ax=plt.subplots(1,2,figsize=[14,6])
for i in range(2):   
    ax[i].bar(range(1,21),y[i][1:21])
    ax[i].set_ylim(-1,1)
    ax[i].set_xticks([1,5,10,15,20])
    ax[i].set_yticks(np.asarray(range(-10,11))*0.1)
    ax[i].hlines(0,0,21,linewidth=1)
    ax[i].hlines([1.96/np.sqrt(arma.shape[0]),-1.96/np.sqrt(arma.shape[0])],0,21,linestyles='dashed',linewidth=1)
    ax[i].set_xlabel('ラグ',fontsize=12)
    ax[i].set_ylabel('自己相関',fontsize=12)
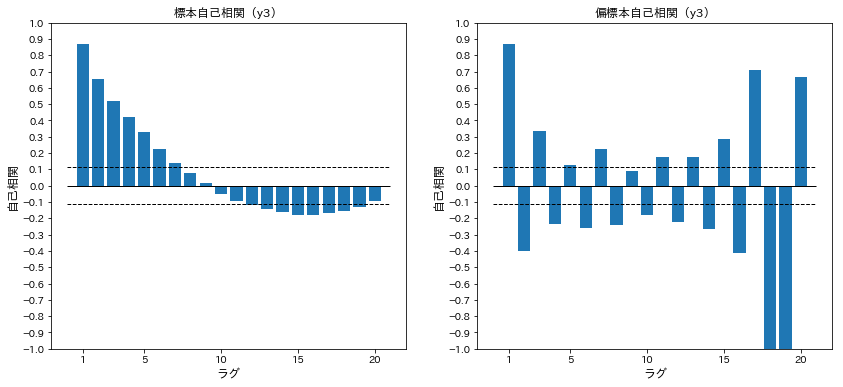
ax[0].set_title('標本自己相関（y3）')
ax[1].set_title('偏標本自己相関（y3）')

plt.show()

output_54_0.png

上記プロットの結果から、季節性があり、ARMAは当てはまらなさそう
ARMA(1,1)、ARMA(1,2)、ARMA(1,3)、ARMA(1,4)、ARMA(2,1)、ARMA(2,2)、ARMA(2,3)、ARMA(2,4)、ARMA(3,1)、ARMA(3,2)、ARMA(3,3)、ARMA(3,4)、ARMA(4,1)、ARMA(4,2)、ARMA(4,3)、ARMA(4,4)をモデル候補とする

arma_1_1=ARMA(arma.y3.values,[1,1]).fit()
arma_1_2=ARMA(arma.y3.values,[1,2]).fit()
arma_1_3=ARMA(arma.y3.values,[1,3]).fit()
arma_1_4=ARMA(arma.y3.values,[1,4]).fit()
arma_2_1=ARMA(arma.y3.values,[2,1]).fit()
arma_2_2=ARMA(arma.y3.values,[2,2]).fit()
arma_2_3=ARMA(arma.y3.values,[2,3]).fit()
arma_2_4=ARMA(arma.y3.values,[2,4]).fit()
arma_3_1=ARMA(arma.y3.values,[3,1]).fit()
arma_3_2=ARMA(arma.y3.values,[3,2]).fit()
arma_3_3=ARMA(arma.y3.values,[3,3]).fit()
arma_3_4=ARMA(arma.y3.values,[3,4]).fit()
arma_4_1=ARMA(arma.y3.values,[4,1]).fit()
arma_4_2=ARMA(arma.y3.values,[4,2]).fit()
arma_4_3=ARMA(arma.y3.values,[4,3]).fit()
arma_4_4=ARMA(arma.y3.values,[4,4]).fit()

model=[arma_1_1,arma_1_2,arma_1_3,arma_1_4,arma_2_1,arma_2_2,arma_2_3,arma_2_4,arma_3_1,arma_3_2,arma_3_3,arma_3_4,arma_4_1,arma_4_2,arma_4_3,arma_4_4]
aic=[]
sic=[]
T=eco.indprod_dlog[1:].shape[0]
for i in range(len(model)):
    aic.append(model[i].aic/T)
    sic.append(model[i].bic/T)
model_sel=pd.DataFrame({'AIC':aic,'SIC':sic},index=['ARMA(1,1)','ARMA(1,2)','ARMA(1,3)','ARMA(1,4)','ARMA(2,1)','ARMA(2,2)','ARMA(2,3)','ARMA(2,4)','ARMA(3,1)','ARMA(3,2)','ARMA(3,3)','ARMA(4,4)','ARMA(4,1)','ARMA(4,2)','ARMA(4,3)','ARMA(4,4)'])
model_sel.T
ARMA(1,1) ARMA(1,2) ARMA(1,3) ARMA(1,4) ARMA(2,1) ARMA(2,2) ARMA(2,3) ARMA(2,4) ARMA(3,1) ARMA(3,2) ARMA(3,3) ARMA(4,4) ARMA(4,1) ARMA(4,2) ARMA(4,3) ARMA(4,4)
AIC 2.537023 2.533205 2.538552 2.543976 2.533802 2.538541 2.531302 2.535771 2.538775 2.544050 2.533076 2.545031 2.543609 2.536865 2.540552 2.546328
SIC 2.577836 2.584221 2.599771 2.615399 2.584818 2.599761 2.602725 2.617397 2.599994 2.615473 2.614702 2.636860 2.615032 2.618491 2.632381 2.648361

AICではARMA(2,3)、SICではARMA(1,1)が選択される
ARMA(2,3)モデルの残差について自己相関検定を行う（ただし、m=10とする）

結果、ARMA(2,3)モデルの残差が自己相関を持つとは言えない（適切なモデルであると言える）

q_m_arma_2_3=acorr_ljungbox(arma_2_3.resid)[0]
p_value_arma_2_3=chi2.sf(q_m_arma_2_3,5)
lag=range(1,41)
test_arma_2_3=pd.DataFrame({'lag':lag,'autocorr':acf_y3[1:],'Q(m)':q_m_arma_2_3,'P_value':p_value_arma_2_3})
test_arma_2_3[['lag','autocorr','Q(m)','P_value']].iloc[0:10,:].T
0 1 2 3 4 5 6 7 8 9
lag 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000
autocorr 0.867000 0.655612 0.519535 0.419404 0.327677 0.223622 0.136581 0.079381 0.017358 -0.049272
Q(m) 0.012603 0.163411 0.333079 0.397876 2.769192 2.770274 4.432651 5.903803 5.942976 6.232675
P_value 0.999999 0.999458 0.996974 0.995388 0.735517 0.735351 0.488945 0.315692 0.311807 0.284232

ARMA(1,1)モデルの残差について自己相関検定を行う（ただし、m=10とする）
結果、ARMA(1,1)モデルの残差が自己相関を持つとは言えない（適切なモデルであると言える）

q_m_arma_1_1=acorr_ljungbox(arma_1_1.resid)[0]
p_value_arma_1_1=chi2.sf(q_m_arma_1_1,8)
lag=range(1,41)
test_arma_1_1=pd.DataFrame({'lag':lag,'autocorr':acf_y3[1:],'Q(m)':q_m_arma_1_1,'P_value':p_value_arma_1_1})
test_arma_1_1[['lag','autocorr','Q(m)','P_value']].iloc[0:10,:].T
0 1 2 3 4 5 6 7 8 9
lag 1.000000 2.000000 3.000000 4.000000 5.000000 6.000000 7.000000 8.000000 9.000000 10.000000
autocorr 0.867000 0.655612 0.519535 0.419404 0.327677 0.223622 0.136581 0.079381 0.017358 -0.049272
Q(m) 1.293730 1.472988 2.071876 2.197028 6.618453 6.624761 7.779293 8.929929 8.950020 9.727831
P_value 0.995627 0.993147 0.978729 0.974368 0.578301 0.577605 0.455321 0.348242 0.346530 0.284651

参考サイト

4
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
3