【第6章】pythonで「経済・ファイナンスデータの計量時系列分析」の章末問題を解く

自分の勉強用に、沖本竜義「経済・ファイナンスデータの計量経済分析」の章末問題をpythonで解いてみました。
jupyter notebook上で記述したものをほぼそのまま載せてあります。
ソースコードの細かい説明は省いてありますが、今後余裕があれば説明を加えようと思います。

こちらの記事は第6章の章末問題を解いたものになります。
第1章、第2章、第4章、第5章、第7章も公開しています。

今回、VECMや共和分検定あたりでpythonの限界を感じましたが、何とかモジュールを用いて解答しています。
Rではなくpythonで時系列分析に取り組んでいる方の参考になれば幸いです。
また、所々かなり怪しい部分があるので、間違っているぞ、もっとうまいやり方があるぞ、というご指摘があれば是非お願いします。

各種設定・モジュールのインポート

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.regression.linear_model import OLS
from statsmodels.tools.tools import add_constant
from arch.unitroot import ADF
from statsmodels.tsa.vector_ar.vecm import VECM
from statsmodels.tsa.vector_ar.vecm import select_coint_rank

import matplotlib as mpl
font = {"family":"IPAexGothic"}
mpl.rc('font', **font)
plt.rcParams["font.size"] = 12

6.4

(1)

ファイルをインポートする

msci = pd.read_csv('./input/msci_day.csv')
print(msci.shape)
msci.head()

(1391, 8)

	Date	ca	fr	ge	it	jp	uk	us
0	2003/1/1	560.099	902.081	724.932	290.187	1593.175	791.076	824.583
1	2003/1/2	574.701	927.206	768.150	296.963	1578.214	797.813	852.219
2	2003/1/3	580.212	929.297	768.411	298.757	1578.411	800.175	851.935
3	2003/1/6	589.619	943.002	788.164	303.273	1619.700	803.966	871.515
4	2003/1/7	585.822	923.785	774.054	297.892	1590.951	793.625	865.992

Date列をdatetime型に変換してecoのDatetimeIndexとする

msci.index=pd.to_datetime(msci.Date.values)
msci.drop('Date',axis=1,inplace=True)
msci.head()

	ca	fr	ge	it	jp	uk	us
2003-01-01	560.099	902.081	724.932	290.187	1593.175	791.076	824.583
2003-01-02	574.701	927.206	768.150	296.963	1578.214	797.813	852.219
2003-01-03	580.212	929.297	768.411	298.757	1578.411	800.175	851.935
2003-01-06	589.619	943.002	788.164	303.273	1619.700	803.966	871.515
2003-01-07	585.822	923.785	774.054	297.892	1590.951	793.625	865.992

欠損データ(e.g. 2005-01-01)があるので、グラフの目盛用にその年で1番最初の日かどうかをカラムに加える

msci['is_year_start']=[msci.index[i].year!=msci.index[i-1].year for i in range(msci.shape[0])]

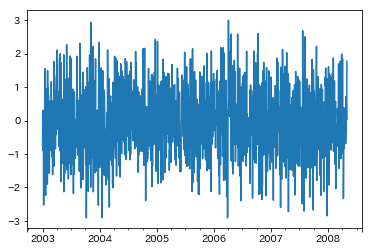
正規ホワイトノイズを生成して追加する

msci['wn']=np.random.randn(msci.shape[0])

プロットする

msci['wn'].plot()
plt.show()

(2)

対数系列を追加する

title=['ca','fr','ge','it','jp','uk','us']
for i in range(len(title)):
    msci['%s_log'%title[i]]=np.log(msci[title[i]])

各国のMSCIの対数系列を正規ホワイトノイズに回帰する

ols=[]
for i in range(len(title)):
    ols.append(OLS(msci['%s_log'%title[i]],add_constant(msci['wn'])).fit())

結果を表示する

beta=[]
pvalue=[]
rsquared=[]
for i in range(len(title)):
    beta.append(ols[i].params[1].round(3))
    pvalue.append(ols[i].pvalues[1].round(3))
    rsquared.append(ols[i].rsquared.round(3))
table=pd.DataFrame({'beta':beta,'Pvalue':pvalue,'R^2':rsquared},index=title,columns=['beta','Pvalue','R^2'])
table

	beta	Pvalue	R^2
ca	-0.003	0.772	0.0
fr	-0.004	0.617	0.0
ge	-0.005	0.596	0.0
it	-0.003	0.696	0.0
jp	0.000	0.993	0.0
uk	-0.003	0.662	0.0
us	-0.002	0.623	0.0

P値は軒並み0.05以上であり、見せかけの回帰は生じていないと考えられる

(3)

ランダムウォークを作成して追加する

rw=[0]
for i in range(msci.shape[0]):
    rw.append(rw[i]+np.random.randn())
msci['rw']=rw[1:]

(4)

各国のMSCIの対数系列をランダムウォークに回帰する

ols=[]
for i in range(len(title)):
    ols.append(OLS(msci['%s_log'%title[i]],add_constant(msci['rw'])).fit())

結果を表示する

beta=[]
pvalue=[]
rsquared=[]
for i in range(len(title)):
    beta.append(ols[i].params[1].round(3))
    pvalue.append(ols[i].pvalues[1].round(3))
    rsquared.append(ols[i].rsquared.round(3))
table=pd.DataFrame({'beta':beta,'Pvalue':pvalue,'R^2':rsquared},index=title,columns=['beta','Pvalue','R^2'])
table

	beta	Pvalue	R^2
ca	0.005	0.000	0.017
fr	0.004	0.000	0.015
ge	0.001	0.175	0.001
it	0.005	0.000	0.034
jp	0.009	0.000	0.097
uk	0.004	0.000	0.023
us	0.002	0.000	0.018

P値は軒並み0.05未満であり、見せかけの回帰が生じていると考えられる

(5)

各国のMSCIの対数系列をランダムウォークとその1期前の値、対数系列の1期前の値に回帰する

ols=[]
for i in range(len(title)):
    X=pd.DataFrame({'rw_t':msci['rw'][1:],'rw_t-1':msci['rw'].shift(1)[1:],'%s_log_t-1'%title[i]:msci['%s_log'%title[i]].shift(1)[1:]},columns=['rw_t','rw_t-1','%s_log_t-1'%title[i]])
    ols.append(OLS(msci['%s_log'%title[i]][1:],add_constant(X)).fit())

結果を表示する

beta=[]
pvalue=[]
rsquared=[]
for i in range(len(title)):
    beta.append(ols[i].params[1].round(3))
    pvalue.append(ols[i].pvalues[1].round(3))
    rsquared.append(ols[i].rsquared.round(3))
table=pd.DataFrame({'beta':beta,'Pvalue':pvalue,'R^2':rsquared},index=title,columns=['beta','Pvalue','R^2'])
table

	beta	Pvalue	R^2
ca	0.0	0.488	0.999
fr	0.0	0.689	0.998
ge	-0.0	0.974	0.999
it	0.0	0.727	0.998
jp	0.0	0.766	0.997
uk	0.0	0.943	0.998
us	-0.0	0.630	0.997

P値は軒並み0.05以上であり、見せかけの回帰は生じていないと考えられる
これは、VARモデルが見せかけの回帰の問題を生じさせないことに起因する（教科書より）

6.5

(1)

ファイルをインポートする

ppp=pd.read_csv('./input/ppp.csv')
print(ppp.shape)
ppp.head()

(396, 8)

	date	cpica	cpijp	cpiuk	cpius	exca	exjp	exuk
0	197401	25.884	44.800	14.861	36.030	0.988	299.00	0.439174
1	197402	26.147	46.267	15.154	36.880	0.969	287.60	0.433651
2	197403	26.410	46.560	15.272	37.035	0.972	276.00	0.417711
3	197404	26.607	47.734	15.800	37.267	0.960	279.75	0.411015
4	197405	27.045	47.930	16.035	37.601	0.962	281.90	0.417885

date列をdatetime型に変換して、pppのDatetimeIndexとする

ppp.index=pd.to_datetime(ppp.date.values,format='%Y%m')
ppp.drop('date',axis=1,inplace=True)
ppp.head()

	cpica	cpijp	cpiuk	cpius	exca	exjp	exuk
1974-01-01	25.884	44.800	14.861	36.030	0.988	299.00	0.439174
1974-02-01	26.147	46.267	15.154	36.880	0.969	287.60	0.433651
1974-03-01	26.410	46.560	15.272	37.035	0.972	276.00	0.417711
1974-04-01	26.607	47.734	15.800	37.267	0.960	279.75	0.411015
1974-05-01	27.045	47.930	16.035	37.601	0.962	281.90	0.417885

対数系列を作成して追加する

for i in range(len(ppp.columns)):
    ppp['l%s'%ppp.columns[i]]=np.log(ppp[ppp.columns[i]])
ppp.head()

	cpica	cpijp	cpiuk	cpius	exca	exjp	exuk	lcpica	lcpijp	lcpiuk	lcpius	lexca	lexjp	lexuk
1974-01-01	25.884	44.800	14.861	36.030	0.988	299.00	0.439174	3.253625	3.802208	2.698740	3.584352	-0.012073	5.700444	-0.822859
1974-02-01	26.147	46.267	15.154	36.880	0.969	287.60	0.433651	3.263734	3.834429	2.718265	3.607669	-0.031491	5.661571	-0.835514
1974-03-01	26.410	46.560	15.272	37.035	0.972	276.00	0.417711	3.273743	3.840742	2.726021	3.611863	-0.028399	5.620401	-0.872966
1974-04-01	26.607	47.734	15.800	37.267	0.960	279.75	0.411015	3.281174	3.865644	2.760010	3.618108	-0.040822	5.633896	-0.889125
1974-05-01	27.045	47.930	16.035	37.601	0.962	281.90	0.417885	3.297502	3.869742	2.774774	3.627031	-0.038741	5.641552	-0.872548

(2)

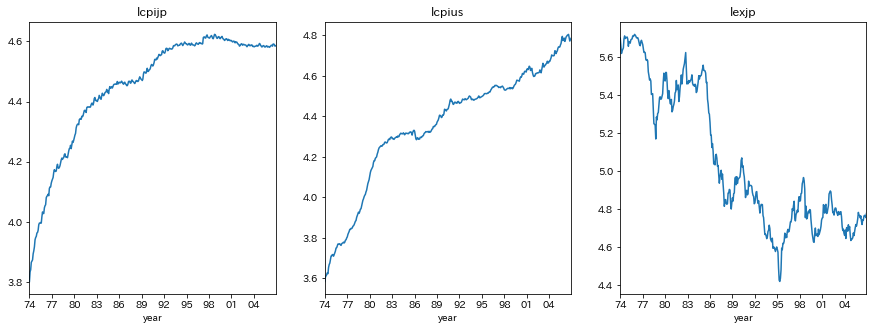
プロットする

title=['lcpijp','lcpius','lexjp']

fig,ax = plt.subplots(nrows=1,ncols=3,figsize=[15,5])
for i in range(3):
    ax[i].plot(ppp[title[i]])
    ax[i].set_title(title[i])
    ax[i].set_xlim(ppp.index[0],ppp.index[-1])
    ax[i].set_xticks(ppp.index[ppp.index.is_year_start][::3])
    ax[i].set_xticklabels(ppp.index[ppp.index.is_year_start][::3].strftime('%y'))
    ax[i].set_xlabel('year')

plt.subplots_adjust(wspace=0.2,hspace=0.3)
plt.show()

5.2の解答に従い、lexjpは場合2、lcpijp,lcpiusは場合3を仮定する
* 場合1...トレンドがなく、期待値が0
* 場合2...トレンドがなく、期待値が0ではない
* 場合3...トレンドがある

trend=['ct','ct','c']
adf=[]
for i in range(len(title)):
    adf.append(ADF(ppp[title[i]],trend=trend[i],max_lags=10,method='AIC'))

ADF検定の結果を表示する

for i in range(len(title)):
    print(title[i])
    print(adf[i])
    print('')

lcpijp
   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -4.417
P-value                         0.002
Lags                               10
-------------------------------------

Trend: Constant and Linear Time Trend
Critical Values: -3.98 (1%), -3.42 (5%), -3.13 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

lcpius
   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -2.170
P-value                         0.507
Lags                                9
-------------------------------------

Trend: Constant and Linear Time Trend
Critical Values: -3.98 (1%), -3.42 (5%), -3.13 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

lexjp
   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -1.507
P-value                         0.530
Lags                                1
-------------------------------------

Trend: Constant
Critical Values: -3.45 (1%), -2.87 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

ADF検定の結果、lcpijpの単位根の帰無仮説は棄却され、lcpius,lexjpの単位根の帰無仮説は採択された
つまり、lcpijpは定常過程であり、lcpius,lexjpは和分過程であることが示唆された

（差分系列のADF検定を行い、単位根過程であることを確定する必要があるが、ここでは省略する）

(3)

lrexjpを作成して追加する

ppp['lrexjp']=ppp['lcpijp']-ppp['lcpius']-ppp['lexjp']

(4)

PPP仮説はlrexjpが定常過程に従うことを示唆する

(5)

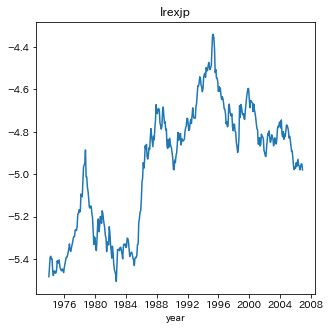
プロットする

fig,ax=plt.subplots(nrows=1,ncols=1,figsize=[5,5])
ax.plot(ppp['lrexjp'])
ax.set_title('lrexjp')
ax.set_xlabel('year')
plt.show()

場合2を仮定する
* 場合1...トレンドがなく、期待値が0
* 場合2...トレンドがなく、期待値が0ではない
* 場合3...トレンドがある

adf=ADF(ppp['lrexjp'],trend='c',max_lags=10,method='AIC')

ADF検定の結果を表示する

print(adf)

   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -1.766
P-value                         0.398
Lags                                1
-------------------------------------

Trend: Constant
Critical Values: -3.45 (1%), -2.87 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

単位根の帰無仮説が採択された
つまり、PPP仮説を支持していない

(6)

PPP仮説を検定する場合共和分ランクは1と仮定するが、ここでは練習も兼ねてトレース検定と最大固有値検定で共和分ランクを決定してみる
モジュールは、pipやcondaではまだ入っていないstatsmodels.tsa.vector_ar.vecmをgithubから直接ダウンロードした

尚、共和分関係は定数を含まず、データは線形トレンドを持つ（VECMが定数項を含める）と仮定した

trace=select_coint_rank(ppp[['lcpijp','lcpius','lexjp']],det_order=-1,k_ar_diff=6,method='trace',signif=0.05)
maxeig=select_coint_rank(ppp[['lcpijp','lcpius','lexjp']],det_order=-1,k_ar_diff=6,method='maxeig',signif=0.05)

トレース検定の結果を表示する

trace.summary()

Johansen cointegration test using trace test statistic with 5% significance level

r_0	r_1	test statistic	critical value
0	3	53.17	24.28
1	3	9.575	12.32

最大固有値検定の結果を表示する

maxeig.summary()

Johansen cointegration test using maximum eigenvalue test statistic with 5% significance level

r_0	r_1	test statistic	critical value
0	1	43.60	17.80
1	2	9.540	11.22

トレース検定と最大固有値検定により、共和分ランクが1であることが示唆された

pythonで「共和分ベクトルが(1,-1,-1)に等しいという制約を課して」VECMを推定する方法が分からなかった（Webで探しましたが見当たりませんでした...どなたか詳しい方ご教授くださると有り難いです...）
そこで、statsmodels.tsa.vector_ar.vecmの共和分ベクトルの推定値beta_tildeを(1,-1,-1)に書き換えることで制約を実現した（このやり方が100%正しい自信はありません）

vecm=VECM(ppp[['lcpijp','lcpius','lexjp']],k_ar_diff=6,coint_rank=1,deterministic='co').fit()

VECMの推定結果を表示する

vecm.summary()

Det. terms outside the coint. relation & lagged endog. parameters for equation lcpijp

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0189	0.005	-3.588	0.000	-0.029	-0.009
L1.lcpijp	0.0950	0.051	1.872	0.061	-0.004	0.195
L1.lcpius	-0.0874	0.039	-2.222	0.026	-0.164	-0.010
L1.lexjp	-0.0123	0.008	-1.615	0.106	-0.027	0.003
L2.lcpijp	-0.2557	0.050	-5.104	0.000	-0.354	-0.158
L2.lcpius	0.1332	0.041	3.238	0.001	0.053	0.214
L2.lexjp	0.0151	0.008	1.991	0.046	0.000	0.030
L3.lcpijp	-0.0331	0.052	-0.642	0.521	-0.134	0.068
L3.lcpius	0.0963	0.042	2.273	0.023	0.013	0.179
L3.lexjp	0.0035	0.008	0.460	0.646	-0.011	0.018
L4.lcpijp	0.0044	0.050	0.087	0.930	-0.094	0.103
L4.lcpius	0.0006	0.043	0.015	0.988	-0.084	0.085
L4.lexjp	0.0120	0.008	1.582	0.114	-0.003	0.027
L5.lcpijp	0.1451	0.049	2.983	0.003	0.050	0.240
L5.lcpius	0.0400	0.042	0.946	0.344	-0.043	0.123
L5.lexjp	-0.0030	0.008	-0.397	0.691	-0.018	0.012
L6.lcpijp	0.1874	0.047	3.978	0.000	0.095	0.280
L6.lcpius	0.0253	0.041	0.623	0.533	-0.054	0.105
L6.lexjp	0.0093	0.008	1.227	0.220	-0.006	0.024

Det. terms outside the coint. relation & lagged endog. parameters for equation lcpius

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0019	0.007	-0.269	0.788	-0.015	0.012
L1.lcpijp	0.1146	0.066	1.729	0.084	-0.015	0.245
L1.lcpius	0.3024	0.051	5.888	0.000	0.202	0.403
L1.lexjp	-0.0004	0.010	-0.040	0.968	-0.020	0.019
L2.lcpijp	-0.0798	0.065	-1.220	0.223	-0.208	0.048
L2.lcpius	-0.1552	0.054	-2.888	0.004	-0.260	-0.050
L2.lexjp	0.0090	0.010	0.903	0.367	-0.010	0.028
L3.lcpijp	0.0471	0.067	0.698	0.485	-0.085	0.179
L3.lcpius	0.2000	0.055	3.614	0.000	0.092	0.308
L3.lexjp	-0.0048	0.010	-0.482	0.630	-0.024	0.015
L4.lcpijp	-0.0291	0.066	-0.444	0.657	-0.158	0.099
L4.lcpius	-0.0749	0.056	-1.334	0.182	-0.185	0.035
L4.lexjp	0.0020	0.010	0.200	0.841	-0.017	0.021
L5.lcpijp	0.0489	0.064	0.770	0.441	-0.076	0.173
L5.lcpius	0.0875	0.055	1.584	0.113	-0.021	0.196
L5.lexjp	0.0192	0.010	1.926	0.054	-0.000	0.039
L6.lcpijp	0.0035	0.062	0.057	0.955	-0.117	0.124
L6.lcpius	0.0315	0.053	0.593	0.553	-0.073	0.136
L6.lexjp	-0.0017	0.010	-0.167	0.868	-0.021	0.018

Det. terms outside the coint. relation & lagged endog. parameters for equation lexjp

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.0356	0.035	1.021	0.307	-0.033	0.104
L1.lcpijp	-0.1846	0.336	-0.550	0.583	-0.843	0.474
L1.lcpius	0.3070	0.260	1.180	0.238	-0.203	0.817
L1.lexjp	0.0646	0.050	1.287	0.198	-0.034	0.163
L2.lcpijp	0.0093	0.331	0.028	0.978	-0.640	0.659
L2.lcpius	0.1640	0.272	0.603	0.547	-0.369	0.697
L2.lexjp	0.0494	0.050	0.984	0.325	-0.049	0.148
L3.lcpijp	-0.2545	0.341	-0.746	0.456	-0.923	0.414
L3.lcpius	-0.1665	0.280	-0.594	0.553	-0.716	0.383
L3.lexjp	0.0996	0.050	1.974	0.048	0.001	0.199
L4.lcpijp	0.5763	0.332	1.737	0.082	-0.074	1.227
L4.lcpius	-0.0397	0.284	-0.140	0.889	-0.597	0.518
L4.lexjp	-0.0298	0.050	-0.592	0.554	-0.128	0.069
L5.lcpijp	-0.3362	0.322	-1.045	0.296	-0.967	0.294
L5.lcpius	0.4754	0.280	1.700	0.089	-0.073	1.024
L5.lexjp	-0.0179	0.050	-0.356	0.722	-0.117	0.081
L6.lcpijp	-0.2922	0.312	-0.938	0.348	-0.903	0.318
L6.lcpius	0.1107	0.269	0.412	0.681	-0.416	0.638
L6.lexjp	-0.1166	0.050	-2.323	0.020	-0.215	-0.018

Loading coefficients (alpha) for equation lcpijp

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	-0.0040	0.001	-3.681	0.000	-0.006	-0.002

Loading coefficients (alpha) for equation lcpius

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	-0.0007	0.001	-0.489	0.625	-0.003	0.002

Loading coefficients (alpha) for equation lexjp

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	0.0080	0.007	1.110	0.267	-0.006	0.022

Cointegration relations for loading-coefficients-column 1

	coef	std err	z	P>|z|	[0.025	0.975]
beta.1	1.0000	0	0	0.000	1.000	1.000
beta.2	-1.0000	0.477	-2.098	0.036	-1.934	-0.066
beta.3	-1.0000	0.318	-3.148	0.002	-1.623	-0.377

共和分ベクトルの値が全て有意である、つまりPPP仮説を支持する
（しかし、前提としてlcpijpが単位根過程ではないため、この結果は意味を持たない）

(7)

まず、各系列に対してADF検定を行い、単位根過程かどうかを確認する

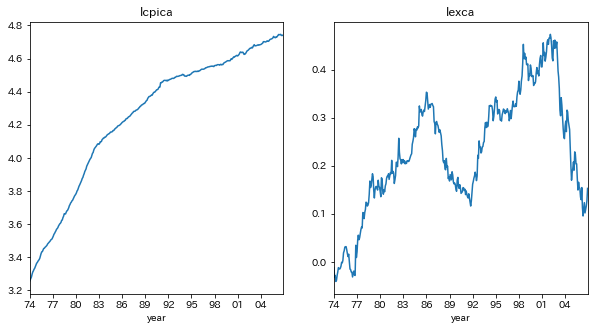
カナダについてプロットする

title=['lcpica','lexca']

fig,ax = plt.subplots(nrows=1,ncols=2,figsize=[10,5])
for i in range(len(title)):
    ax[i].plot(ppp[title[i]])
    ax[i].set_title(title[i])
    ax[i].set_xlim(ppp.index[0],ppp.index[-1])
    ax[i].set_xticks(ppp.index[ppp.index.is_year_start][::3])
    ax[i].set_xticklabels(ppp.index[ppp.index.is_year_start][::3].strftime('%y'))
    ax[i].set_xlabel('year')

plt.subplots_adjust(wspace=0.2,hspace=0.3)
plt.show()

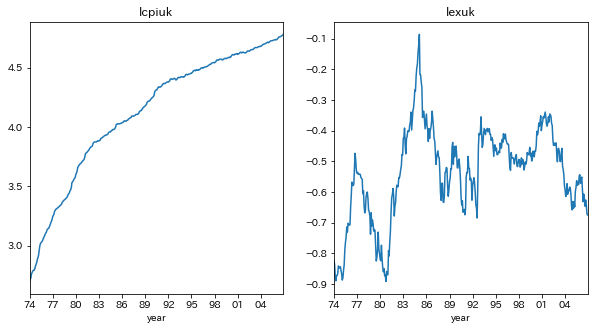
イギリスについてプロットする

title=['lcpiuk','lexuk']

fig,ax = plt.subplots(nrows=1,ncols=2,figsize=[10,5])
for i in range(len(title)):
    ax[i].plot(ppp[title[i]])
    ax[i].set_title(title[i])
    ax[i].set_xlim(ppp.index[0],ppp.index[-1])
    ax[i].set_xticks(ppp.index[ppp.index.is_year_start][::3])
    ax[i].set_xticklabels(ppp.index[ppp.index.is_year_start][::3].strftime('%y'))
    ax[i].set_xlabel('year')

plt.subplots_adjust(wspace=0.2,hspace=0.3)
plt.show()

5.2の解答に従い、lexca,lexukは場合2、lcpica,lcpiukは場合3を仮定する
* 場合1...トレンドがなく、期待値が0
* 場合2...トレンドがなく、期待値が0ではない
* 場合3...トレンドがある

title=['lcpica','lexca','lcpiuk','lexuk']
trend=['ct','c','ct','c']
adf=[]
for i in range(len(title)):
    adf.append(ADF(ppp[title[i]],trend=trend[i],max_lags=10,method='AIC'))

ADF検定の結果を表示する

for i in range(len(title)):
    print(title[i])
    print(adf[i])
    print('')

lcpica
   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -2.523
P-value                         0.316
Lags                                4
-------------------------------------

Trend: Constant and Linear Time Trend
Critical Values: -3.98 (1%), -3.42 (5%), -3.13 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

lexca
   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -1.934
P-value                         0.316
Lags                                0
-------------------------------------

Trend: Constant
Critical Values: -3.45 (1%), -2.87 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

lcpiuk
   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -5.057
P-value                         0.000
Lags                                8
-------------------------------------

Trend: Constant and Linear Time Trend
Critical Values: -3.98 (1%), -3.42 (5%), -3.13 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

lexuk
   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -2.541
P-value                         0.106
Lags                                1
-------------------------------------

Trend: Constant
Critical Values: -3.45 (1%), -2.87 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

ADF検定の結果、lcpiukの単位根の帰無仮説は棄却され、lcpica,lexca,lexukの単位根の帰無仮説は採択された
つまり、lcpiukは定常過程であり、lcpica,lexca,lexukは和分過程であることが示唆された

（差分系列のADF検定を行い、単位根過程であることを確定する必要があるが、ここでは省略する）

カナダとアメリカ、イギリスとアメリカの間にPPP仮説が成立していることをEngle-Granger共和分検定（=(5)の方法）を用いて検定する

lrexca,lrexukを作成して追加する

ppp['lrexca']=ppp['lcpica']-ppp['lcpius']-ppp['lexca']
ppp['lrexuk']=ppp['lcpiuk']-ppp['lcpius']-ppp['lexuk']

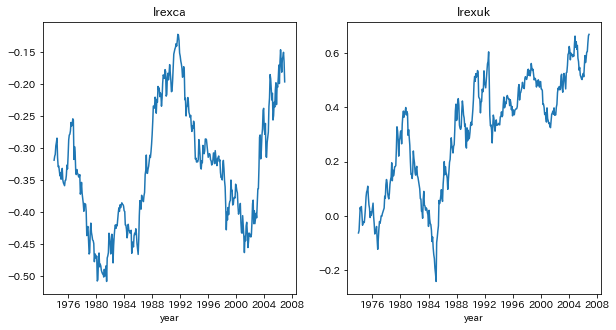
プロットする

title=['lrexca','lrexuk']
fig,ax=plt.subplots(nrows=1,ncols=2,figsize=[10,5])
for i in range(2):
    ax[i].plot(ppp[title[i]])
    ax[i].set_title(title[i])
    ax[i].set_xlabel('year')
plt.show()

場合2を仮定する
* 場合1...トレンドがなく、期待値が0
* 場合2...トレンドがなく、期待値が0ではない
* 場合3...トレンドがある

adf=[]
for i in range(len(title)):
    adf.append(ADF(ppp[title[i]],trend='c',max_lags=10,method='AIC'))

ADF検定の結果を表示する

for i in range(len(title)):
    print(adf[i])
    print('')

   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -1.371
P-value                         0.596
Lags                                0
-------------------------------------

Trend: Constant
Critical Values: -3.45 (1%), -2.87 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

   Augmented Dickey-Fuller Results   
=====================================
Test Statistic                 -1.597
P-value                         0.485
Lags                                1
-------------------------------------

Trend: Constant
Critical Values: -3.45 (1%), -2.87 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.

どちらの場合も、単位根の帰無仮説が採択された
つまり、PPP仮説を支持していない

以上の議論でPPP仮説が成立していないと結論づけられるが、共和分ベクトルが(1,-1,-1)に等しいという制約を課してVECMを推定し、カナダとアメリカ、イギリスとアメリカの間にPPP仮説が成立していることを検定してみる
尚、共和分関係は定数を含まず、データは線形トレンドを持つ（VECMが定数項を含める）と仮定した

トレース検定と最大固有値検定で共和分ランクを決定してみる

country=['ca','uk']
trace=[]
maxeig=[]
for i in range(len(country)): 
    trace.append(select_coint_rank(ppp[['lcpi%s'%country[i],'lcpius','lex%s'%country[i]]],det_order=-1,k_ar_diff=6,method='trace',signif=0.05))
    maxeig.append(select_coint_rank(ppp[['lcpi%s'%country[i],'lcpius','lex%s'%country[i]]],det_order=-1,k_ar_diff=6,method='maxeig',signif=0.05))

カナダとアメリカの結果を表示する

display(trace[0].summary())
display(maxeig[0].summary())

Johansen cointegration test using trace test statistic with 5% significance level

r_0	r_1	test statistic	critical value
0	3	52.24	24.28
1	3	5.263	12.32

Johansen cointegration test using maximum eigenvalue test statistic with 5% significance level

r_0	r_1	test statistic	critical value
0	1	46.98	17.80
1	2	4.069	11.22

カナダとアメリカの共和分ランクは1であることが示唆された

イギリスとアメリカの結果を表示する

display(trace[1].summary())
display(maxeig[1].summary())

Johansen cointegration test using trace test statistic with 5% significance level

r_0	r_1	test statistic	critical value
0	3	54.46	24.28
1	3	15.15	12.32
2	3	1.652	4.130

Johansen cointegration test using maximum eigenvalue test statistic with 5% significance level

r_0	r_1	test statistic	critical value
0	1	39.31	17.80
1	2	13.50	11.22
2	3	1.652	4.130

イギリスとアメリカの共和分ランクは2であることが示唆された
この時点でppp仮説に矛盾するが、以下では共和分ランクが1と仮定して進める

共和分ベクトルが(1,-1,-1)に等しいという制約を課してVECMを推定する

vecm=[]
for i in range(len(country)):
    vecm.append(VECM(ppp[['lcpi%s'%country[i],'lcpius','lex%s'%country[i]]],k_ar_diff=6,coint_rank=1,deterministic='co').fit())

カナダとアメリカの結果を表示する

vecm[0].summary()

Det. terms outside the coint. relation & lagged endog. parameters for equation lcpica

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0005	0.001	-0.882	0.378	-0.002	0.001
L1.lcpica	0.0675	0.053	1.264	0.206	-0.037	0.172
L1.lcpius	0.1558	0.027	5.702	0.000	0.102	0.209
L1.lexca	0.0102	0.011	0.944	0.345	-0.011	0.031
L2.lcpica	0.1464	0.053	2.771	0.006	0.043	0.250
L2.lcpius	-0.1098	0.029	-3.824	0.000	-0.166	-0.054
L2.lexca	0.0274	0.011	2.526	0.012	0.006	0.049
L3.lcpica	0.0917	0.052	1.769	0.077	-0.010	0.193
L3.lcpius	0.0611	0.029	2.102	0.036	0.004	0.118
L3.lexca	0.0040	0.011	0.366	0.714	-0.018	0.026
L4.lcpica	0.2135	0.052	4.140	0.000	0.112	0.315
L4.lcpius	-0.0260	0.029	-0.894	0.371	-0.083	0.031
L4.lexca	-0.0017	0.011	-0.155	0.877	-0.023	0.020
L5.lcpica	0.0317	0.052	0.616	0.538	-0.069	0.133
L5.lcpius	0.0519	0.029	1.793	0.073	-0.005	0.109
L5.lexca	0.0175	0.011	1.583	0.113	-0.004	0.039
L6.lcpica	0.0685	0.051	1.353	0.176	-0.031	0.168
L6.lcpius	-0.0208	0.028	-0.739	0.460	-0.076	0.034
L6.lexca	-0.0285	0.011	-2.583	0.010	-0.050	-0.007

Det. terms outside the coint. relation & lagged endog. parameters for equation lcpius

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.0012	0.001	1.033	0.302	-0.001	0.004
L1.lcpica	-0.0373	0.103	-0.362	0.718	-0.239	0.165
L1.lcpius	0.3372	0.053	6.393	0.000	0.234	0.441
L1.lexca	-0.0012	0.021	-0.060	0.952	-0.042	0.040
L2.lcpica	0.0629	0.102	0.617	0.537	-0.137	0.263
L2.lcpius	-0.2105	0.055	-3.797	0.000	-0.319	-0.102
L2.lexca	-0.0242	0.021	-1.155	0.248	-0.065	0.017
L3.lcpica	0.0346	0.100	0.346	0.729	-0.161	0.231
L3.lcpius	0.2332	0.056	4.155	0.000	0.123	0.343
L3.lexca	0.0343	0.021	1.616	0.106	-0.007	0.076
L4.lcpica	0.2794	0.100	2.807	0.005	0.084	0.474
L4.lcpius	-0.1440	0.056	-2.563	0.010	-0.254	-0.034
L4.lexca	-0.0418	0.021	-1.967	0.049	-0.083	-0.000
L5.lcpica	-0.0911	0.099	-0.916	0.360	-0.286	0.104
L5.lcpius	0.0944	0.056	1.690	0.091	-0.015	0.204
L5.lexca	0.0305	0.021	1.431	0.152	-0.011	0.072
L6.lcpica	0.0267	0.098	0.273	0.785	-0.165	0.218
L6.lcpius	0.0342	0.054	0.628	0.530	-0.072	0.141
L6.lexca	0.0136	0.021	0.637	0.524	-0.028	0.055

Det. terms outside the coint. relation & lagged endog. parameters for equation lexca

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.0013	0.003	0.443	0.658	-0.004	0.007
L1.lcpica	-0.1364	0.252	-0.541	0.589	-0.631	0.358
L1.lcpius	0.1105	0.129	0.856	0.392	-0.143	0.364
L1.lexca	-0.0029	0.051	-0.056	0.955	-0.103	0.097
L2.lcpica	-0.0998	0.250	-0.400	0.689	-0.589	0.389
L2.lcpius	-0.0967	0.136	-0.713	0.476	-0.363	0.169
L2.lexca	-0.0287	0.051	-0.560	0.576	-0.129	0.072
L3.lcpica	-0.0666	0.245	-0.272	0.786	-0.546	0.413
L3.lcpius	-0.0694	0.137	-0.505	0.613	-0.339	0.200
L3.lexca	0.0357	0.052	0.687	0.492	-0.066	0.138
L4.lcpica	0.2033	0.244	0.835	0.404	-0.274	0.681
L4.lcpius	-0.0686	0.138	-0.499	0.618	-0.338	0.201
L4.lexca	0.0362	0.052	0.696	0.486	-0.066	0.138
L5.lcpica	-0.0315	0.243	-0.130	0.897	-0.509	0.445
L5.lcpius	-0.0541	0.137	-0.396	0.692	-0.322	0.214
L5.lexca	0.0204	0.052	0.391	0.696	-0.082	0.123
L6.lcpica	0.3883	0.239	1.624	0.104	-0.080	0.857
L6.lcpius	0.0664	0.133	0.499	0.617	-0.194	0.327
L6.lexca	-0.0389	0.052	-0.747	0.455	-0.141	0.063

Loading coefficients (alpha) for equation lcpica

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	-0.0046	0.002	-2.387	0.017	-0.008	-0.001

Loading coefficients (alpha) for equation lcpius

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	0.0012	0.004	0.311	0.755	-0.006	0.008

Loading coefficients (alpha) for equation lexca

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	0.0046	0.009	0.504	0.615	-0.013	0.022

Cointegration relations for loading-coefficients-column 1

	coef	std err	z	P>|z|	[0.025	0.975]
beta.1	1.0000	0	0	0.000	1.000	1.000
beta.2	-1.0000	0.192	-5.215	0.000	-1.376	-0.624
beta.3	-1.0000	0.375	-2.665	0.008	-1.735	-0.265

共和分ベクトルの値が全て有意である、つまりPPP仮説を支持する
これは、Engle-Granger共和分検定の結果と矛盾する

この矛盾が、vecmモジュールの使い方を間違えただけなのか、本当にEngle-Granger共和分検定と制約付きVECM推定で検定結果が異なっているのか、わかりません...（どなたかご教授くださると幸いです...）

カナダとアメリカの結果を表示する

vecm[1].summary()

Det. terms outside the coint. relation & lagged endog. parameters for equation lcpiuk

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.0026	0.001	3.578	0.000	0.001	0.004
L1.lcpiuk	0.3108	0.049	6.360	0.000	0.215	0.407
L1.lcpius	-0.0034	0.042	-0.081	0.936	-0.086	0.079
L1.lexuk	0.0020	0.009	0.230	0.818	-0.015	0.019
L2.lcpiuk	0.0583	0.052	1.127	0.260	-0.043	0.160
L2.lcpius	0.0008	0.043	0.020	0.984	-0.084	0.085
L2.lexuk	-0.0063	0.009	-0.711	0.477	-0.024	0.011
L3.lcpiuk	-0.0110	0.052	-0.211	0.833	-0.112	0.091
L3.lcpius	0.0604	0.044	1.374	0.169	-0.026	0.147
L3.lexuk	0.0032	0.009	0.360	0.719	-0.014	0.021
L4.lcpiuk	-0.0246	0.051	-0.486	0.627	-0.124	0.075
L4.lcpius	0.0474	0.044	1.069	0.285	-0.039	0.134
L4.lexuk	-0.0070	0.009	-0.789	0.430	-0.024	0.010
L5.lcpiuk	0.0643	0.050	1.282	0.200	-0.034	0.163
L5.lcpius	-0.0222	0.044	-0.505	0.614	-0.108	0.064
L5.lexuk	-0.0022	0.009	-0.253	0.800	-0.020	0.015
L6.lcpiuk	0.1910	0.048	3.949	0.000	0.096	0.286
L6.lcpius	0.1596	0.042	3.807	0.000	0.077	0.242
L6.lexuk	0.0080	0.009	0.905	0.365	-0.009	0.025

Det. terms outside the coint. relation & lagged endog. parameters for equation lcpius

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0011	0.001	-1.298	0.194	-0.003	0.001
L1.lcpiuk	0.1845	0.057	3.249	0.001	0.073	0.296
L1.lcpius	0.2662	0.049	5.444	0.000	0.170	0.362
L1.lexuk	0.0041	0.010	0.395	0.693	-0.016	0.024
L2.lcpiuk	0.0066	0.060	0.110	0.913	-0.111	0.124
L2.lcpius	-0.1982	0.050	-3.954	0.000	-0.297	-0.100
L2.lexuk	-0.0051	0.010	-0.499	0.618	-0.025	0.015
L3.lcpiuk	0.0669	0.060	1.112	0.266	-0.051	0.185
L3.lcpius	0.1860	0.051	3.640	0.000	0.086	0.286
L3.lexuk	-0.0093	0.010	-0.908	0.364	-0.029	0.011
L4.lcpiuk	-0.0235	0.059	-0.400	0.689	-0.139	0.092
L4.lcpius	-0.1080	0.051	-2.099	0.036	-0.209	-0.007
L4.lexuk	0.0026	0.010	0.248	0.804	-0.018	0.023
L5.lcpiuk	-0.0038	0.058	-0.065	0.948	-0.118	0.110
L5.lcpius	0.0347	0.051	0.679	0.497	-0.065	0.135
L5.lexuk	0.0088	0.010	0.859	0.391	-0.011	0.029
L6.lcpiuk	0.2322	0.056	4.133	0.000	0.122	0.342
L6.lcpius	-0.0253	0.049	-0.519	0.603	-0.121	0.070
L6.lexuk	-0.0081	0.010	-0.789	0.430	-0.028	0.012

Det. terms outside the coint. relation & lagged endog. parameters for equation lexuk

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0039	0.004	-0.908	0.364	-0.012	0.004
L1.lcpiuk	0.0767	0.282	0.272	0.786	-0.477	0.630
L1.lcpius	0.2137	0.243	0.879	0.379	-0.263	0.690
L1.lexuk	0.0800	0.051	1.566	0.117	-0.020	0.180
L2.lcpiuk	0.1946	0.299	0.651	0.515	-0.391	0.780
L2.lcpius	-0.1638	0.249	-0.657	0.511	-0.653	0.325
L2.lexuk	0.0171	0.051	0.336	0.737	-0.083	0.117
L3.lcpiuk	-0.0480	0.299	-0.160	0.873	-0.635	0.539
L3.lcpius	-0.2528	0.254	-0.995	0.320	-0.751	0.245
L3.lexuk	-0.0121	0.051	-0.237	0.813	-0.112	0.088
L4.lcpiuk	0.1079	0.292	0.369	0.712	-0.465	0.681
L4.lcpius	-0.2078	0.256	-0.812	0.417	-0.709	0.294
L4.lexuk	0.0321	0.051	0.628	0.530	-0.068	0.132
L5.lcpiuk	0.4523	0.290	1.561	0.118	-0.115	1.020
L5.lcpius	0.3716	0.254	1.464	0.143	-0.126	0.869
L5.lexuk	0.0287	0.051	0.563	0.574	-0.071	0.128
L6.lcpiuk	-0.2310	0.279	-0.827	0.408	-0.779	0.316
L6.lcpius	-0.2250	0.242	-0.929	0.353	-0.700	0.250
L6.lexuk	-0.0676	0.051	-1.328	0.184	-0.167	0.032

Loading coefficients (alpha) for equation lcpiuk

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	-0.0043	0.002	-2.799	0.005	-0.007	-0.001

Loading coefficients (alpha) for equation lcpius

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	0.0038	0.002	2.101	0.036	0.000	0.007

Loading coefficients (alpha) for equation lexuk

	coef	std err	z	P>|z|	[0.025	0.975]
ec1	0.0074	0.009	0.828	0.407	-0.010	0.025

Cointegration relations for loading-coefficients-column 1

	coef	std err	z	P>|z|	[0.025	0.975]
beta.1	1.0000	0	0	0.000	1.000	1.000
beta.2	-1.0000	0.247	-4.046	0.000	-1.484	-0.516
beta.3	-1.0000	0.464	-2.155	0.031	-1.909	-0.091

共和分ベクトルの値が全て有意である、つまりPPP仮説を支持する
（しかし、前提としてlcpijpが単位根過程ではないため、この結果は意味を持たない）

参考サイト

ARCHのドキュメント
: http://arch.readthedocs.io/en/latest/index.html
statsmodels.tsa.vector_ar.vecmのソースコード
:https://github.com/statsmodels/statsmodels/blob/master/statsmodels/tsa/vector_ar/vecm.py