様々な補間法と最小2乗法をPythonで理解する のうち、「Scipy.interpolate を使った様々な補間法」を、実データっぽい模擬データを解析するように書き直したサンプルプログラムです。
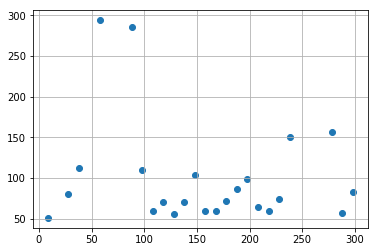
実データっぽい模擬データ
こういうデータを補間したいとしましょう。
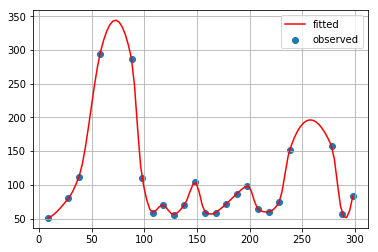
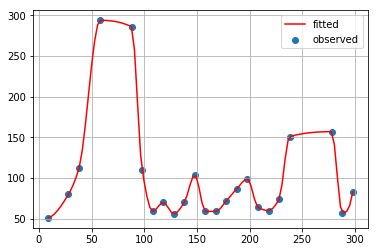
x_observed = [9, 28, 38, 58, 88, 98, 108, 118, 128, 138, 148, 158, 168, 178, 188, 198, 208, 218, 228, 238, 278, 288, 298]
y_observed = [51, 80, 112, 294, 286, 110, 59, 70, 56, 70, 104, 59, 59, 72, 87, 99, 64, 60, 74, 151, 157, 57, 83]
まずはデータの図示
こういうデータですね。
%matplotlib inline
import matplotlib.pyplot as plt
plt.scatter(x_observed, y_observed)
plt.grid()
補間する x 座標を作る
実データの最小値から最大値までの間に等間隔に100ポイント作りました。
import numpy as np
x_latent = np.linspace(min(x_observed), max(x_observed), 100)
Scipy で使用可能な様々な補間法
こんなに使えて便利ですね。
from scipy import interpolate
ip1 = ["最近傍点補間", lambda x, y: interpolate.interp1d(x, y, kind="nearest")]
ip2 = ["線形補間", interpolate.interp1d]
ip3 = ["ラグランジュ補間", interpolate.lagrange]
ip4 = ["重心補間", interpolate.BarycentricInterpolator]
ip5 = ["Krogh補間", interpolate.KroghInterpolator]
ip6 = ["2次スプライン補間", lambda x, y: interpolate.interp1d(x, y, kind="quadratic")]
ip7 = ["3次スプライン補間", lambda x, y: interpolate.interp1d(x, y, kind="cubic")]
ip8 = ["秋間補間", interpolate.Akima1DInterpolator]
ip9 = ["区分的 3 次エルミート補間", interpolate.PchipInterpolator]
補間してみましょう。
補間法の違いによって、結果は様々です。
for method_name, method in [ip1, ip2, ip3, ip4, ip5, ip6, ip7, ip8, ip9]:
print(method_name)
fitted_curve = method(x_observed, y_observed)
plt.scatter(x_observed, y_observed, label="observed")
plt.plot(x_latent, fitted_curve(x_latent), c="red", label="fitted")
plt.grid()
plt.legend()
plt.show()
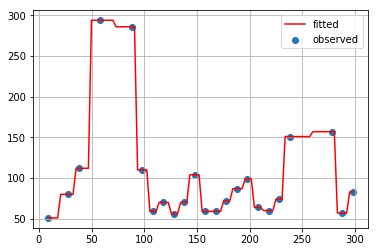
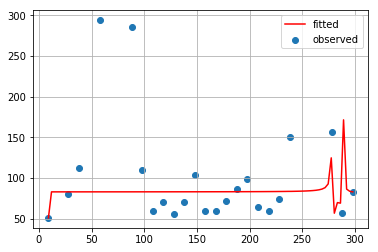
最近傍点補間
線形補間
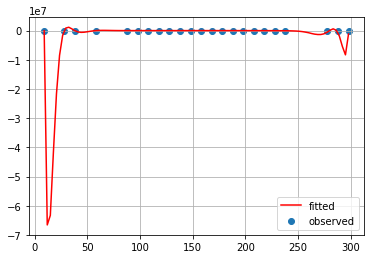
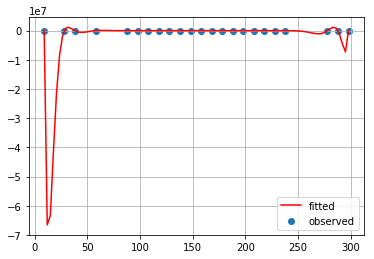
ラグランジュ補間
重心補間
Krogh補間
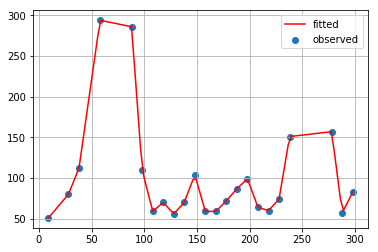
2次スプライン補間
3次スプライン補間
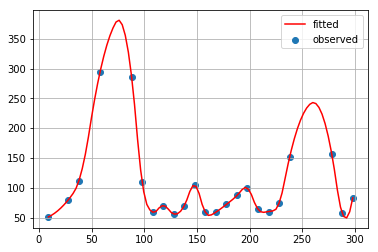
秋間補間
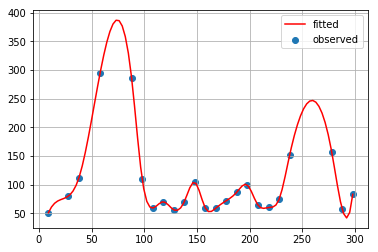
区分的 3 次エルミート補間
参考
Numpy.polyfit を使ったカーブフィッティング もご参考にどうぞ。