強化学習 今日から学習

あなたにはこれから、北海道の札幌から沖縄の那覇まで旅行していただきます。強化学習で。

この日本縦断旅行には、以下の２つの目標があります。

• 目標１：ゴールにたどり着く。 まずはゴールにたどり着かないことにはどうにもなりません。
• 目標２：最短経路を発見する。 ゴールまでの経路を発見したら、その中で最短のものを発見します。

そして、以下のルールを適用したいと思います。

• 一度訪れた都市は二度と訪問しない。間違えて二度同じ都市を訪れたらゲームオーバー。

グラフ探索手法を使えばいいんじゃない？

ええ、その通りです。グラフ探索手法を使えば簡単に求まります。詳しくは

• グラフ理論の基礎
• グラフ理論の基礎をmatplotlibアニメーションで

を見てください。でもここでは、強化学習について今日から学習していただくのが目的です。

日本の県庁所在地データ

グラフ理論の基礎、グラフ理論の基礎をmatplotlibアニメーションでで用いた以下のデータを用います。

県庁所在地の緯度・経度

県庁所在地の緯度・経度データをダウンロードします。

import urllib.request
url = 'https://raw.githubusercontent.com/maskot1977/ipython_notebook/master/toydata/location.txt'
urllib.request.urlretrieve(url, 'location.txt') # データのダウンロード

('location.txt', <http.client.HTTPMessage at 0x110e78ba8>)

ダウンロードしたデータを読み込みます。

import pandas as pd
location = pd.read_csv('location.txt').values
pd.DataFrame(location)

	0	1	2
0	Sapporo	43.0642	141.347
1	Aomori	40.8244	140.74
2	Morioka	39.7036	141.153
3	Sendai	38.2689	140.872
...	...	...	...
44	Miyazaki	31.9111	131.424
45	Kagoshima	31.5603	130.558
46	Naha	26.2125	127.681

47 rows × 3 columns

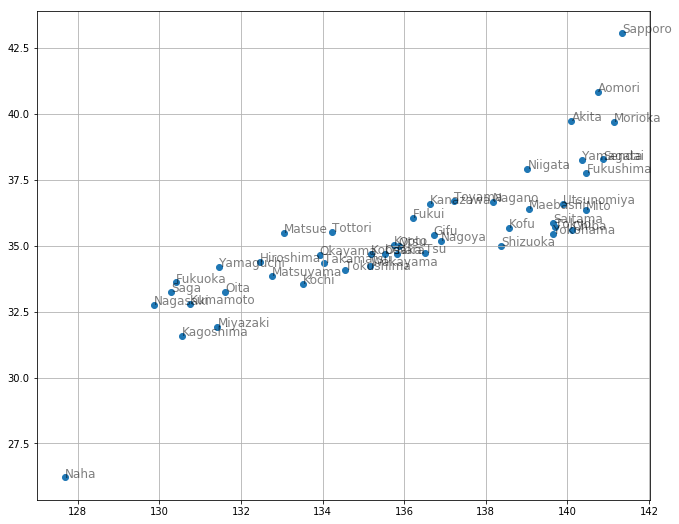
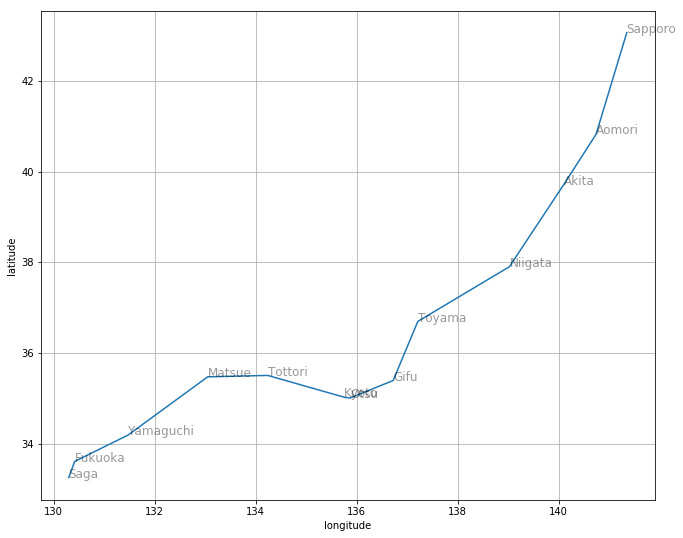
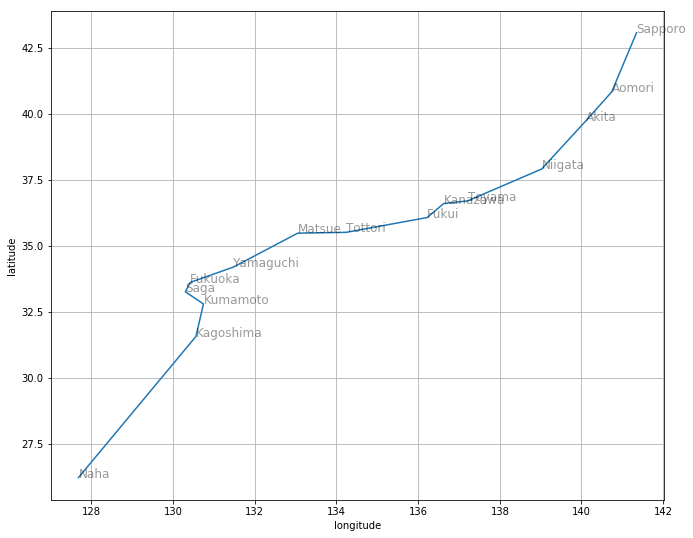
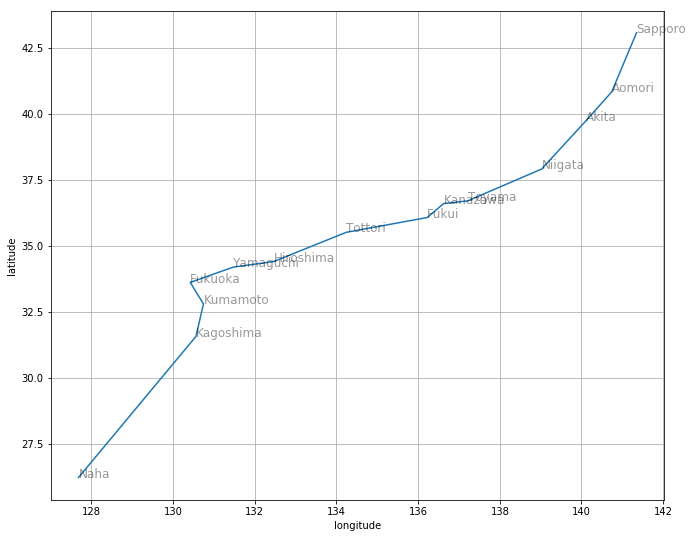
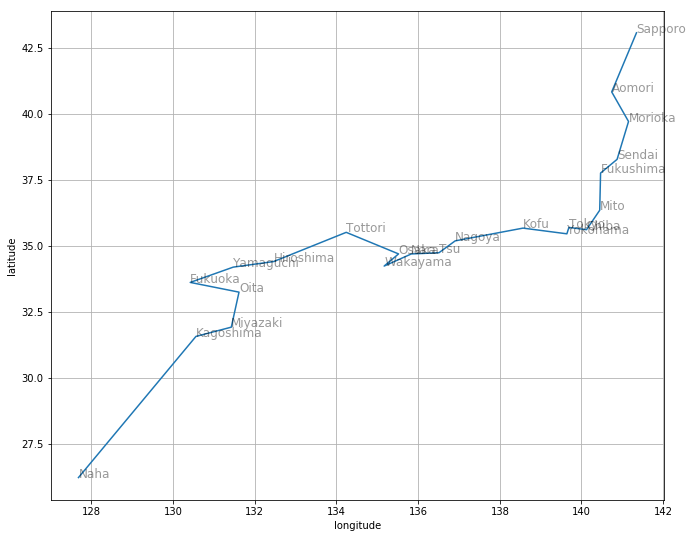
読み込んだデータを可視化しましょう。

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(11, 9))
plt.scatter(location[:, 2], location[:, 1])
for city, y, x in location:
    plt.text(x, y, city, alpha=0.5, size=12)
plt.grid()

県庁所在地間の徒歩移動

県庁所在地間を徒歩で移動すると何時間かかるか、グーグルマップで調べてみたデータがあります（徒歩で移動できない場合はフェリーを使うものとします）。これをダウンロードします。

url = 'https://raw.githubusercontent.com/maskot1977/ipython_notebook/master/toydata/walk.txt'
urllib.request.urlretrieve(url, 'walk.txt')

('walk.txt', <http.client.HTTPMessage at 0x1220b8a58>)

ダウンロードしたデータを読み込みます。

walk = pd.read_csv('walk.txt', sep='\s+')
walk

	Town1	Town2	Hour	Ferry
0	Sapporo	Aomori	55	True
1	Akita	Aomori	36	NaN
2	Akita	Sendai	45	NaN
3	Akita	Niigata	52	NaN
...	...	...	...	...
96	Nagasaki	Kumamoto	18	NaN
97	Nagasaki	Saga	20	NaN
98	Kagoshima	Naha	26	NaN

99 rows × 4 columns

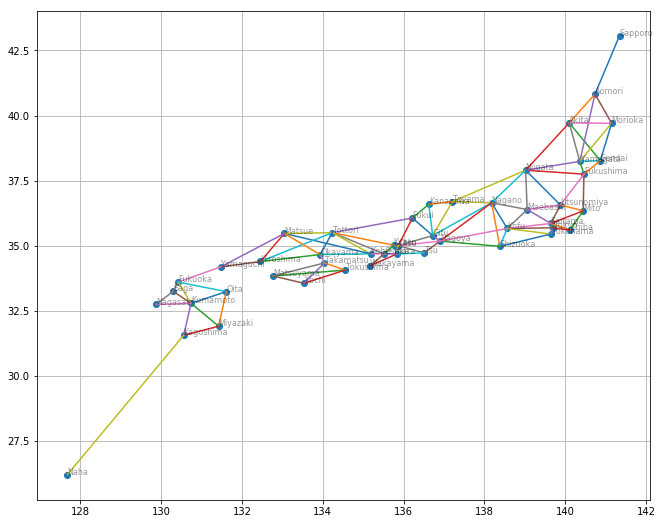
あれ？鹿児島-那覇間がフェリーになってないことに今気づいた...まあいいや、今回のデータ解析に影響はない。ここで得られた都市間の関係を可視化しましょう。

plt.figure(figsize=(11, 9))
for city, y, x in location:
    plt.text(x, y, city, alpha=0.4, size=8)
    
for w in walk.values:
    t1 = np.where(location[:, 0] == w[0])[0][0]
    t2 = np.where(location[:, 0] == w[1])[0][0]
    n1, y1, x1 = location[t1]
    n2, y2, x2 = location[t2]
    plt.plot([x1, x2], [y1, y2])
    
plt.scatter(location[:, 2], location[:, 1])
plt.grid()

この県庁所在地の都市を「頂点」、都市と都市の間の線を「辺」と呼び、頂点と頂点が辺で直接結ばれていることを隣接していると呼ぶことにします。せっかく都市間の徒歩移動時間のデータがあるのですが、解釈を簡単にするため、以降の解析では「辺」の情報は用いますが、徒歩移動時間のデータは使いません。

県庁所在地間の距離行列

県庁所在地の緯度・経度から、県庁所在地間の距離行列を求めましょう。

import numpy as np
from scipy.spatial import distance

dist_mat = distance.cdist(location[:, 1:], location[:, 1:], metric='euclidean') # ユークリッド距離

行列をカラーマップで可視化する関数を作ります。

import pandas as pd
def visualize_matrix(matrix):
    plt.figure(figsize=(12, 10))
    plt.imshow(matrix, interpolation='nearest', cmap=plt.cm.coolwarm)
    plt.colorbar()
    tick_marks = np.arange(len(matrix))
    plt.xticks(tick_marks, matrix.columns, rotation=90)
    plt.yticks(tick_marks, matrix.columns)
    plt.tight_layout()

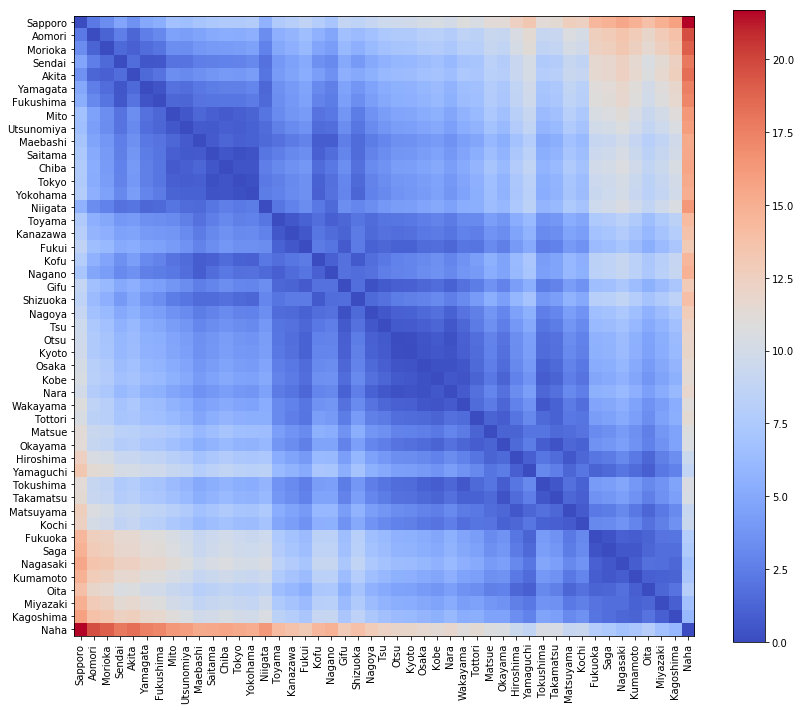
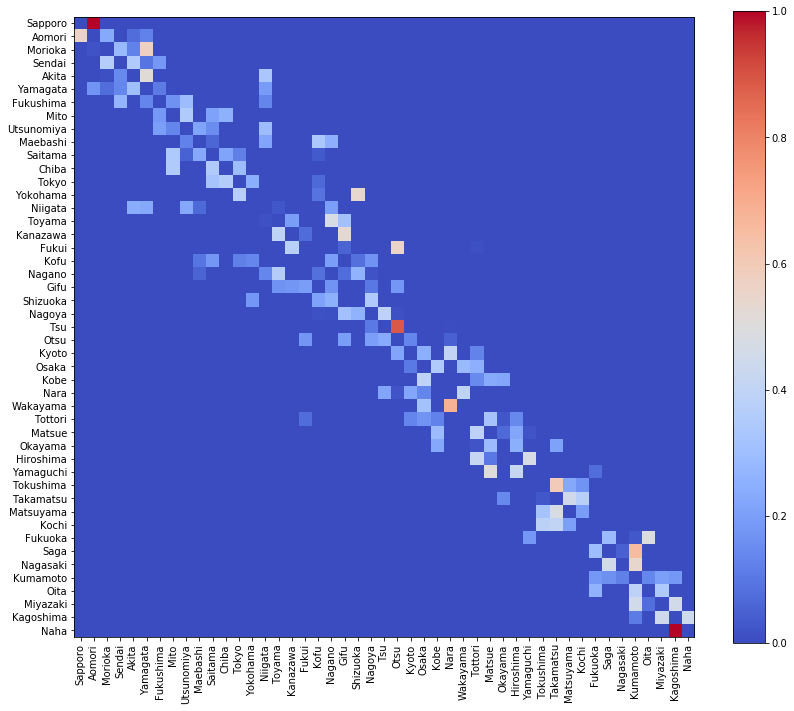
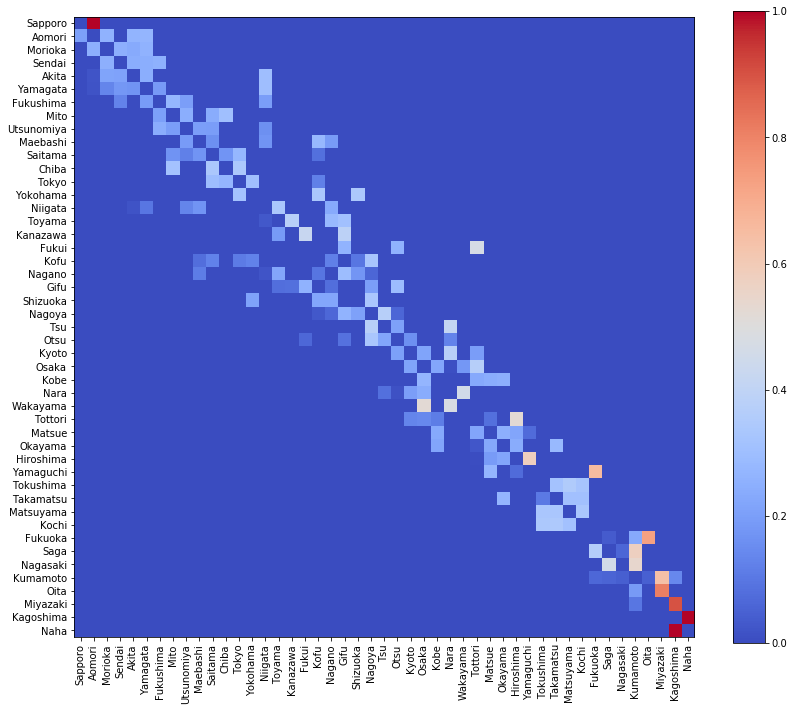
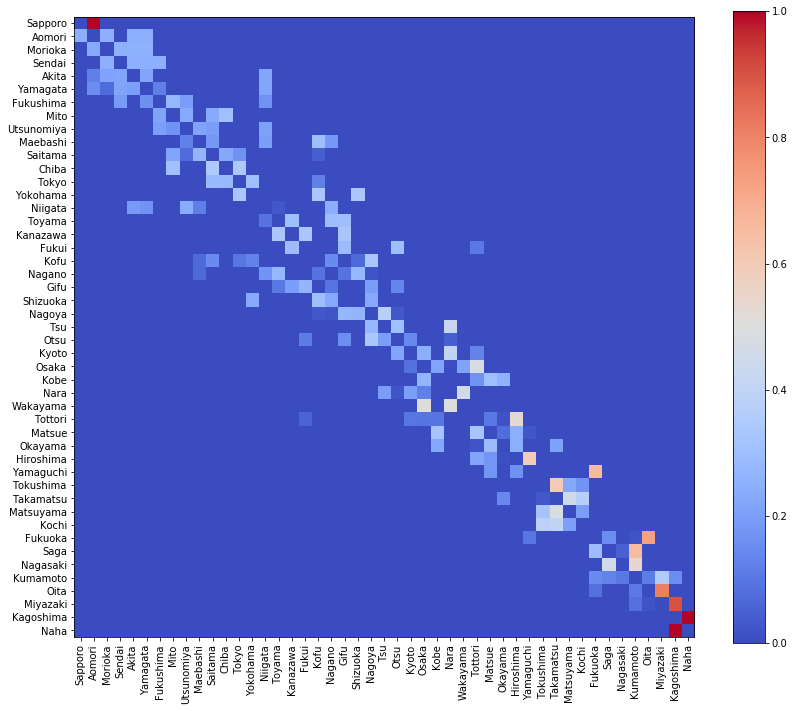
得られた距離行列を可視化すると

visualize_matrix(pd.DataFrame(dist_mat, columns=location[:, 0]))

この距離行列を、今回の解析では、２つの用途に使います。

• ひとつは、現在地から、目的地である那覇までの距離の計算。
• もうひとつは、出発地である札幌から、現在地までの総移動距離の計算。

エージェント

強化学習では、学習する「頭脳」にあたるものを「エージェント」と呼びます。エージェントは、取れる行動の選択肢を把握し、学習を通じて、その行動の判断の重みを調整して行きます。

取れる行動の選択肢シータ

変数シータ（θ, theta）は、そのとき取れる行動の選択肢を表すものとします。グラフ理論で言えば、「辺」（頂点と頂点の接続関係）を表します。計算してみましょう。

import numpy as np
theta_zero = np.full((len(location), len(location)), np.nan)

for w in walk.values:
    i = np.where(location[:, 0] == w[0])[0][0]
    j = np.where(location[:, 0] == w[1])[0][0]
    theta_zero[i, j] = 1
    theta_zero[j, i] = 1

以上のようにすれば、都市 $i$ と隣接している都市の番号は theta_zero[i] で得られます。

取る行動の確率パイ

変数パイ（π, pi）は、そのとき取る行動の確率を表すものとします。グラフ理論で言えば、「辺の重み」を表します。強化学習では、この pi を「ポリシー」（方策）と呼び、これを最適化することになります。

まずは初期値として、選択肢が複数ある場合に、その中から１つを等しい確率でランダムに選択する場合を考えます。

def normalize_pi(theta):
    [m, n] = theta.shape
    pi = np.zeros((m, n))
    for i in range(0, m):
        pi[i, :] = theta[i, :] / np.nansum(theta[i, :])
        
    return np.nan_to_num(pi)

このようにして、 pi の初期値 pi_zero を求めます。

pi_zero = normalize_pi(theta_zero)

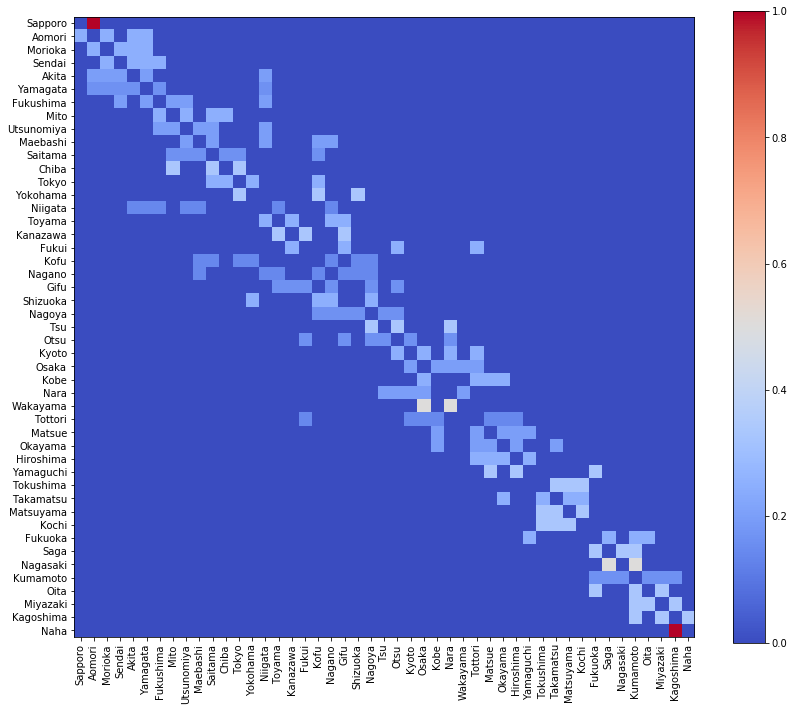
pi_zero を可視化しましょう。

visualize_matrix(pd.DataFrame(pi_zero, columns=location[:, 0]))

ここで注意すべきは、 pi_zero が対称行列ではないことです。たとえば、札幌から青森に向かう辺と、青森から札幌に向かう辺がありますが、その重みは一緒ではありません。なぜなら、このグラフにおいては、札幌から次の都市へ向かう選択肢は１つしかないのに対し、青森から次の都市へ向かう選択肢は複数あるからです。

「行動」と「状態」について

強化学習では、「行動」と「状態」を区別して取り扱います。ある状態において、ある行動を選択した結果、異なる状態へ遷移します。

この記事で取り扱う例は、「行動」と「状態」を区別しなくても良い特殊な例です。つまり、「状態」は「そのときいる都市」を指し、「行動」は「次に行く都市」を指し、それが次の「状態」になります。行動と状態を区別しなくても良い分、コードが簡単になります。

ランダムウォーク

まずは、このポリシー pi が pi_zero のままの状態で日本縦断旅行を試みましょう。ある都市に着いたら、次にどの都市に行くかをランダムに決定するランダムウォークになります。

次の行動を確率的に選ぶ

ポリシー pi が示す確率に従って、次の都市を選ぶ関数を作ります。

def get_next(town, pi):
    return np.random.choice(range(len(pi)), p=pi[town, :])

たとえば、 pi_zero に従って、東京（１２番）の次の都市は次のように求められます。

get_next(12, pi_zero)

13

ランダムに決定しているため、当然、実行のたびに結果は変わります。

ランダムウォークによる探索

それでは、ランダムウォークによる探索を行いましょう。

def explore(pi, start=0, goal=46): # スタートは0（札幌）、ゴールは46（那覇）
    route = [start] # 旅行履歴を入れるリスト
    town = start
    while True:
        next_town = get_next(town, pi) # 次の都市を決定する
        if next_town in route: # 同じ都市を二度訪問したら
            break # ゲームオーバー

        route.append(next_town) # 次の都市を履歴に入れる

        if next_town == goal: # ゴールに到着
            break # おめでとうございます
        else: # まだゴールじゃない
            town = next_town # 「次の都市」を「現在位置」とする

    return route

pi_zero に従ってランダムウォークを開始

route = explore(pi_zero)
route

[0, 1, 2, 3, 4, 5]

ランダムなので、もちろん実行のたびに結果が変わります。都市の番号だけだとイメージしにくい場合は、次のようにして都市名に変換したらイメージしやすいでしょう。

[location[i, 0] for i in route]

['Sapporo', 'Aomori', 'Morioka', 'Sendai', 'Akita', 'Yamagata']

この例では、札幌から山形まで歩いて、その次の行き先で間違えて訪問済みの都市を選んでしまったのでゲームオーバーです。

さて、こんなランダムウォークで、果たして札幌から那覇まで辿り着けるでしょうか？

探索結果の評価指標

探索結果の良し悪しを評価する方法を作りましょう。現在地から目的地（那覇）までの直線距離と、出発地（札幌）から現在地までの総移動距離を計算します。

def evaluate(route, goal=46):
    dist_goal = dist_mat[route[-1], goal]
    len_route = sum([dist_mat[route[i], route[i + 1]] for i in range(len(route) - 1)])
    return [dist_goal, len_route]

dist_goal は「現在地から目的地（那覇）までの直線距離」、 len_route は「出発地（札幌）から現在地までの総移動距離」です。

では、実行例です。

route = explore(pi_zero)
[location[i, 0] for i in route], evaluate(route)

(['Sapporo', 'Aomori'], [19.597025248636594, 2.3205099949149073])

この例では、札幌から青森へ行き、青森から札幌へ戻る道を選択してしまってゲームオーバー。 現在地（青森）から目的地（那覇）までの距離は 19.597025248636594 で、出発地（札幌）から現在地（青森）までの距離は 2.3205099949149073 というわけです。

日本縦断旅行の目標として、この dist_goal がゼロになる経路を探し、その中で len_route が最小のものを探すことになります。 len_route が短ければ良いというものではありません。

今から、札幌から那覇まで移動するゲームを何度もトライしますが、ある結果が得られた時に、これまでの中で最も良いものなのかどうかを判定する関数を作りましょう。

best_dist_goal = 1000000 # ありえないほど大きな値を初期値にする
best_len_route = 1000000 # ありえないほど大きな値を初期値にする

def is_best_ever():
    if best_dist_goal >= dist_goal: # ベスト dist_goal 値と同じかそれより小さいなら
        if best_dist_goal > dist_goal: # 過去のベスト dist_goal 値より小さいなら
            return True # これまでの中で最も良い
        elif best_len_route > len_route: # 過去のベスト len_route 値より小さいなら
            return True # これまでの中で最も良い
        else:
            return False # 最良ではない
    else:
        return False # 最良ではない

探索実行

では、準備は出来上がったので、ランダムウォークによる探索を５万回繰り返します。

%%time # 実行時間を計測
pi = pi_zero.copy() # pi の初期化
theta = theta_zero.copy() # theta の初期化

best_dist_goal = 1000000 # ありえないほど大きな値を初期値にする
best_len_route = 1000000 # ありえないほど大きな値を初期値にする

dist_goal_history0 = [] # dist_goal の履歴
len_route_history0 = [] # len_route の履歴
best_route0 = [] # ベスト経路

for itera in range(50000): # ５万回繰り返す
    route = explore(pi) # 探索
    dist_goal, len_route = evaluate(route) # 評価
    dist_goal_history0.append(dist_goal) # 記録
    len_route_history0.append(len_route) # 記録
    
    if is_best_ever(): # 過去のベストなら
        best_dist_goal = dist_goal # ベスト dist_goal
        best_len_route = len_route # ベスト len_route
        best_route0 = route # ベスト経路

CPU times: user 10 s, sys: 118 ms, total: 10.2 s
Wall time: 11.8 s

探索結果

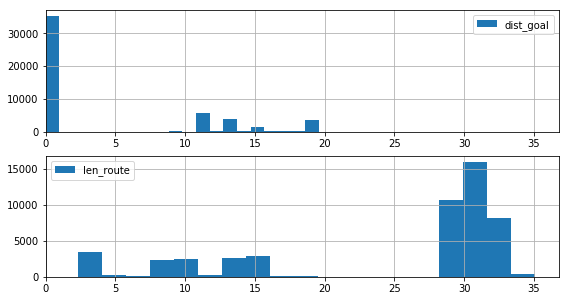
結果を可視化する関数を作ります。まずは、得られた dist_goal len_route の分布を可視化する関数

def draw_histgrams(dist_goal_history, len_route_history):
    plt.figure(figsize=(max(len_route_history) / 4, max(dist_goal_history) / 4))
    x_max = max(dist_goal_history + len_route_history)
    ax = plt.subplot(2,1,1)
    ax.hist(dist_goal_history, label='dist_goal', bins=20)
    ax.set_xlim([0, x_max])
    ax.grid()
    ax.legend()
    ax = plt.subplot(2,1,2)
    ax.hist(len_route_history, label='len_route', bins=20)
    ax.set_xlim([0, x_max])
    ax.grid()
    ax.legend()

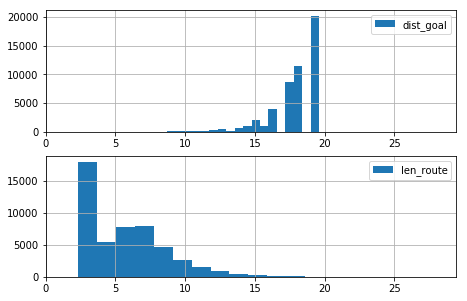
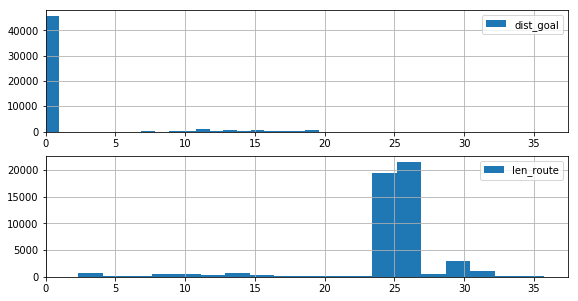
draw_histgrams(dist_goal_history0, len_route_history0)

札幌からスタートして那覇へはなかなかたどり着きません。運が良ければたどり着くことはありますが。探索の初期でゲームオーバーになるケースが多いことが分かります。

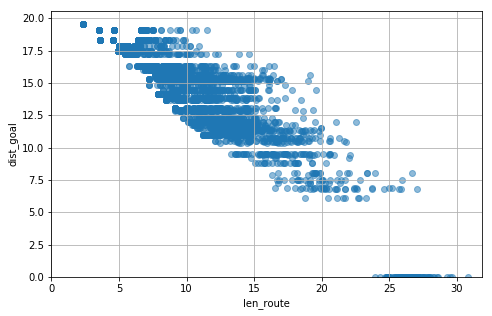
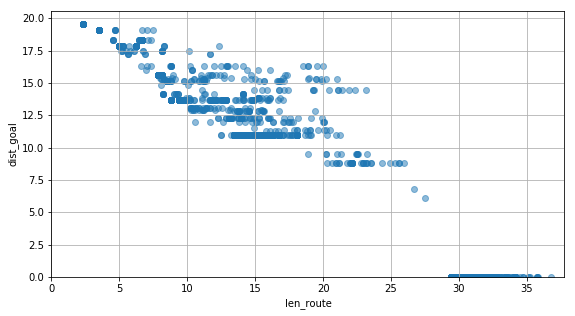
次に、 dist_goal len_route の関係を見てみましょう。

def draw_scatter(dist_goal_history, len_route_history):
    plt.figure(figsize=(max(len_route_history) / 4, max(dist_goal_history) / 4))
    plt.scatter(len_route_history, dist_goal_history, alpha=0.5)
    plt.ylabel('dist_goal')
    plt.xlabel('len_route')
    plt.ylim([0, max(dist_goal_history) + 1])
    plt.xlim([0, max(len_route_history) + 1])
    plt.grid()
    plt.show()

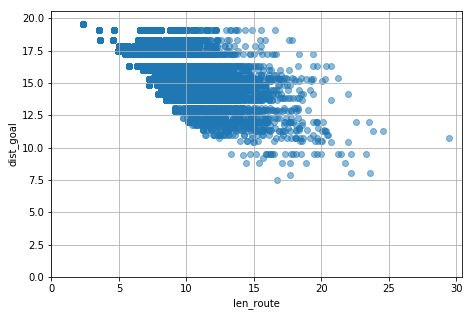
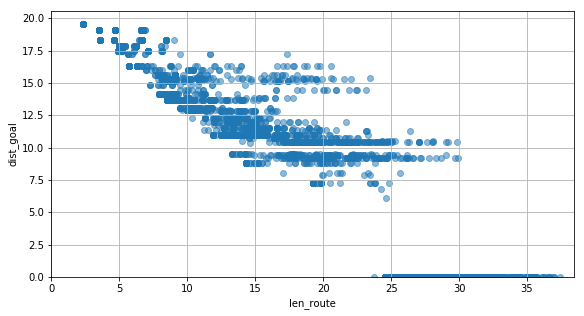
draw_scatter(dist_goal_history0, len_route_history0)

那覇までたどり着けていないこと、そして、ゲームオーバーになった場所が同じでも、そこに至るまでの移動距離には幅がある（いろんな経路を選択している）ことが分かります。

次に、 dist_goal len_route がどのように推移していったか見てみましょう。

def visualize_history(history, interval=50, window=50):
    plt.plot(range(0, len(history), interval),  # 全体の最大値
             [np.array(history)[:i].max() for i in range(len(history)) if (i%interval) == 1], label='max')
    plt.plot(range(window, len(history)+window, interval), 
             [np.array(history)[i:i + window].mean() for i in range(len(history)) if (i%interval) == 1], 
             label='mean(recent)') # 最近 interval 回の平均値
    plt.plot(range(0, len(history), interval), 
             [np.array(history)[:i].mean() for i in range(len(history)) if (i%interval) == 1], label='mean') # 全体の平均値
    plt.plot(range(0, len(history), interval), 
             [np.array(history)[:i].min() for i in range(len(history)) if (i%interval) == 1], label='min') # 全体の最小値
    plt.legend()
    plt.grid()
    plt.show()

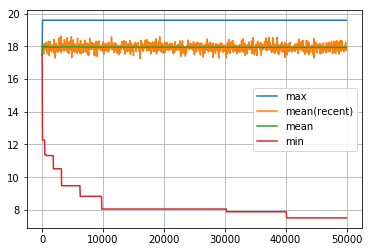
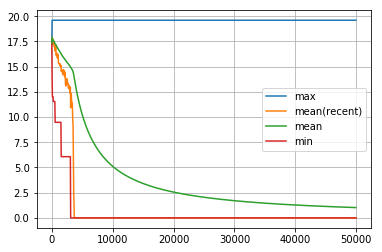
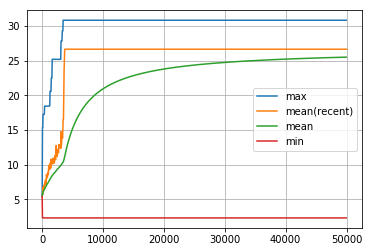
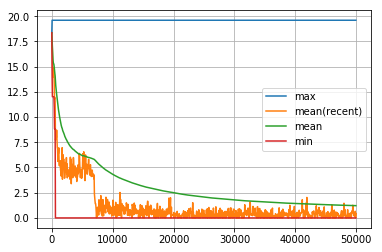
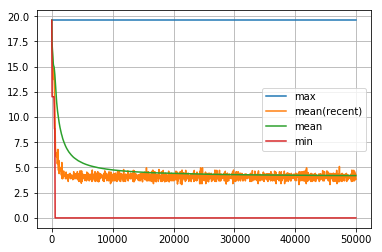
visualize_history(dist_goal_history0)

dist_goal は、たまに最小値を更新することはありますが、那覇まではたどり着かず。そして、何度探索を繰り返しても、その平均値が改善されることはありません。何も学習していないから当然です。

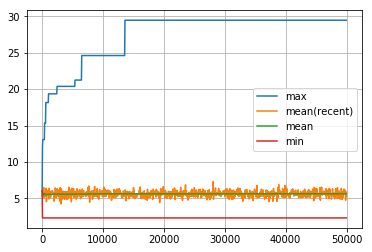
visualize_history(len_route_history0)

同様に len_route も、たまに最大値を更新することはありますが、那覇まではたどり着かず、何度探索を繰り返しても、その平均値が改善されることはありません。何も学習していないから当然です。

では最後に、このランダムウォークで見出したベストな経路を表示してみましょう。

def draw_route(route):
    plt.figure(figsize=(11, 9))
    for i in route:
        plt.text(location[i, 2], location[i, 1], location[i, 0], alpha=0.4, size=12)
    plt.grid()
    plt.plot([location[i][2] for i in route], [location[i][1] for i in route])
    plt.ylabel('latitude')
    plt.xlabel('longitude')
    plt.show()

draw_route(best_route0)

めっちゃ頑張ったのに、佐賀までしか辿り着けませんでした。運が良ければ、那覇にたどり着くことはあります。でもそれを学習することはありません。

方策勾配法

それでは、いよいよ 強化学習 の開始です。強化学習の手法は大きく 方策勾配法 (Policy gradient method) と 価値反復法 (Value iteration method) の２つに分けられるようです。まずは方策勾配法をやりましょう。

ポリシー pi を更新する

得られた経路 route は、「その経路の終点がゴールにどのくらい近いか」という視点で、良し悪しを評価できます。ゴールまでの距離が小さいほど、今後の探索で、その経路上の辺を選ぶ確率が高くなるように、ポリシー pi を更新しましょう。

def update_pi(pi, route, goal=46, eta=0.1): # イータ（η, eta） は学習率
    new_pi = pi.copy() # numpy array をコピー
    for i in range(len(route) - 1): # 経路上の各辺に対して
        town1 = route[i] # 辺iの起点の都市
        town2 = route[i + 1] # 辺iの終点の都市
        new_pi[town1, town2] +=  eta / (dist_mat[route[-1], goal] + 1)
        # 経路の終点がゴールに近ければ近いほど高い得点が得られるようにする
    
    return normalize_pi(new_pi) # pi を更新する

最後に normalize_pi を用いるのは、行の値の和が 1.0 になるように調整するためです。

探索実行

では、探索を開始しましょう。

%%time
pi = pi_zero.copy()

best_dist_goal = 1000000
best_len_route = 1000000

dist_goal_history1 = []
len_route_history1 = []
best_route1 = []
for itera in range(50000):
    route = explore(pi)
    dist_goal, len_route = evaluate(route)
    dist_goal_history1.append(dist_goal)
    len_route_history1.append(len_route)
        
    pi = update_pi(pi, route)
    
    if is_best_ever():
        best_dist_goal = dist_goal
        best_len_route = len_route
        best_route1 = route

CPU times: user 59.9 s, sys: 340 ms, total: 1min
Wall time: 1min 1s

探索結果

以下が結果の一例です。結果は実行のたびに異なり、場合によっては、５万回学習を繰り返しても目的地の那覇にたどり着かないことがあります。

得られた dist_goal len_route の分布は、ランダムウォークによる分布と大きく異なります。目的地の那覇に到着する回数が圧倒的に多くなりました。

draw_histgrams(dist_goal_history1, len_route_history1)

dist_goal len_route の関係は次のようになりました。

draw_scatter(dist_goal_history1, len_route_history1)

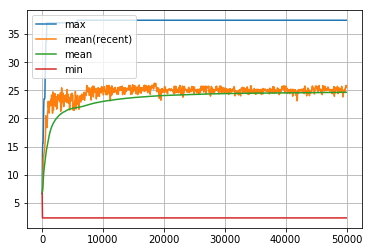
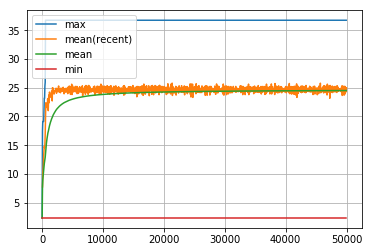
dist_goal の履歴です。ランダムウォークと比べて圧倒的に早い時期に目的地の那覇に到達し、しかも、その後は目的地に簡単に到着できるようになりました。

visualize_history(dist_goal_history1)

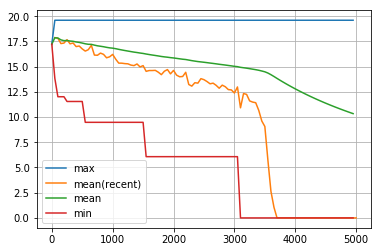
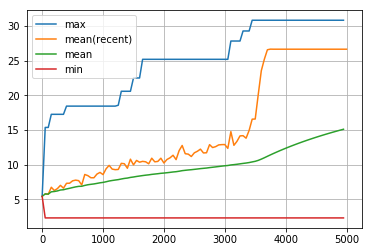
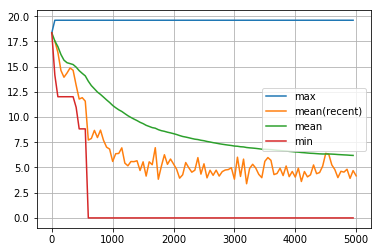
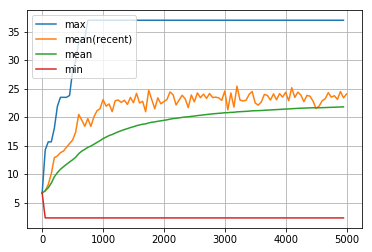
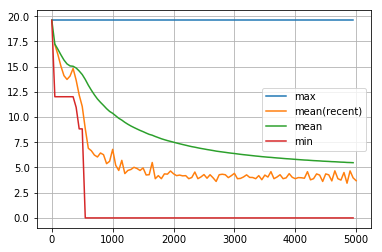
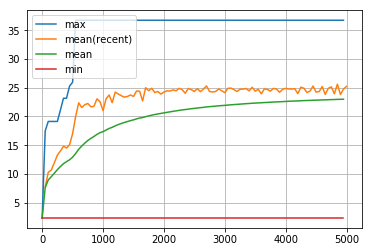
dist_goal の履歴のうち、最初の５０００回です。

visualize_history(dist_goal_history1[:5000])

同様に、len_route の履歴です。

visualize_history(len_route_history1)

len_route の履歴の最初の５０００回です。

visualize_history(len_route_history1[:5000])

ベストの経路として出力されたのがこちらです。最短経路に近いものが選ばれているのが分かります。ひとつだけ、惜しい。福岡から佐賀を経由して熊本に行っています。ここは、佐賀を経由せず、福岡から直接熊本に向かうべきでした。

draw_route(best_route1)

得られたポリシー pi を、別名pi_pgとして保存しておきましょう。

pi_pg = pi.copy()

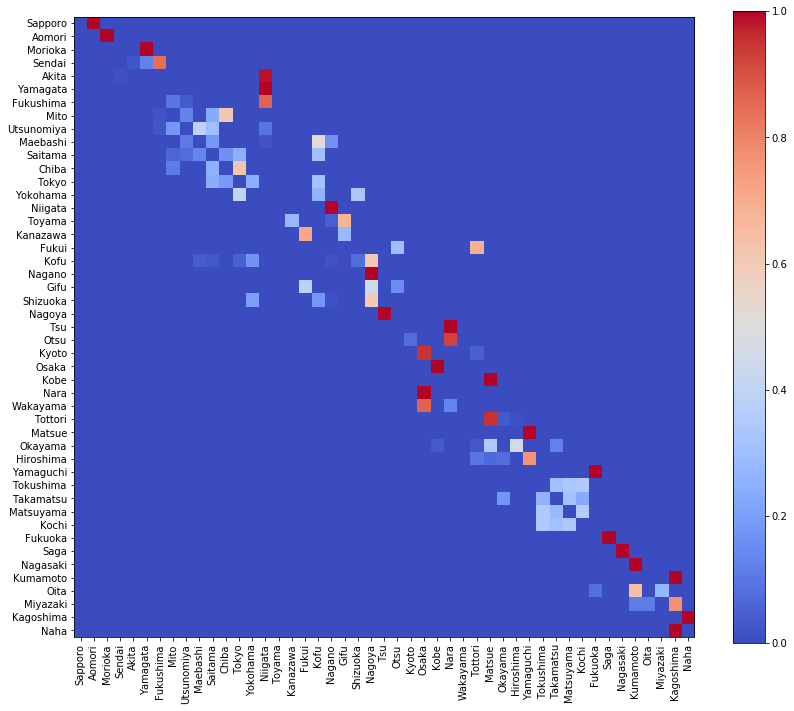
そのポリシーpi_pgを可視化

visualize_matrix(pd.DataFrame(pi_pg, columns=location[:, 0]))

絶対的に重要な経路は赤くなっています。たとえば、鹿児島に到着したら、次は那覇しかあり得ません。それ以外（熊本、宮崎）を選択しては絶対にダメです。それをよく表しています。

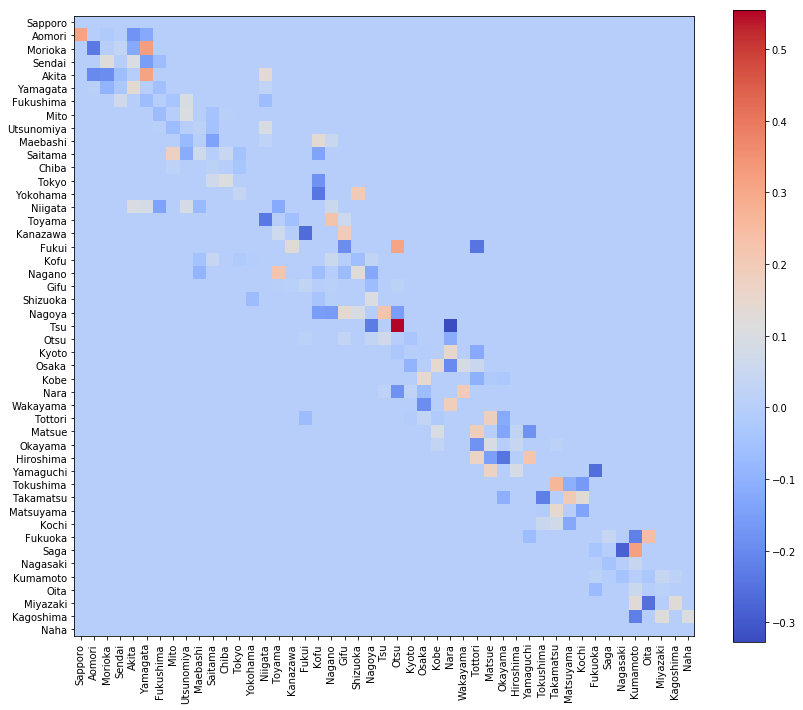
初期値と比べてどう変わったかはこのようにして確認できます。

visualize_matrix(pd.DataFrame(pi_pg - pi_zero, columns=location[:, 0]))

重要ではない場所はほとんど変化していません。たとえば、四国地方や関東地方はあまり重要ではないようです。

Epsilon-Greedy法

上記の「方策勾配法」に対して、ここで紹介するEpsilon-Greedy法 と、その次に紹介するQ学習は「価値反復法」(Value Iteration Method)と呼ばれます。

価値反復法では、ポリシーはなぜか「π」ではなく「Q」と呼ばれるようです。piが完全な均等確率からスタートするのに対し、Qは、均等ではないランダムな確率からスタートします。

ポリシーQ

def generate_Q(theta): # 取れる選択肢 theta から、均等ではないランダム確率を生成
    [m, n] = theta.shape
    Q = np.zeros((m, n))
    rand = np.random.rand(m, n)
    for i in range(m):
        for j in range(n):
            if theta[i, j] == 1:
                Q[i, j] = rand[i, j]
        
    return normalize_pi(Q)

均等ではないポリシーQの初期値Q_zeroを生成します

Q_zero = generate_Q(theta_zero)

生成したQ_zeroを可視化します。

visualize_matrix(pd.DataFrame(Q_zero, columns=location[:, 0]))

Q_zeroとpiの違いはこのようになります。

visualize_matrix(pd.DataFrame(Q_zero - pi_zero, columns=location[:, 0]))

次の行動の選び方

方策勾配法では、次の行動get_nextはポリシーpiの示す確率に従いランダムに選択しました。価値反復法では、次の行動get_nextを次のように書き換えます。

def get_next(town, Q, epsilon=0.1):
    if np.random.rand() < epsilon:
        return np.random.choice(range(len(Q)), p=Q[town, :])
    else:
        return np.nanargmax(Q[town, :])

つまり、新たなパラメータepsilonを導入し、ポリシーQの示す確率に従いランダムに行動を選択する場合と、ポリシーQが最大値をとる行動を選択する場合とを生じさせるのです。最初はepsilonは大きめの値を設定します。つまり、ランダムな選択をする機会を多くします。その後、次第にepsilonを小さくし、ランダムな選択をする機会を少なくしていきます。

報酬

「報酬」(reward)という概念も導入し、目的を達成したら（ゴールに着いたら）１点、失敗したら（同じ都市を二度訪問しゲームオーバーになったら）-１点、途中経過は０点とします。

次に示す sarsa という方法では、ある行動（経路上の辺）に対するQ値を更新する際に、その次の行動（経路上の次の辺）のQ値も参照しながら更新します。このとき、時間割引率gammaをかけます。

def sarsa(town, Q, prev_t, next_t, reward, eta=0.1, gamma=0.9, goal=46):
    if reward == 1: #dist_mat[town, goal] == 0:
        Q[prev_t, town] = Q[prev_t, town] + eta * (reward - Q[prev_t, town])
    elif reward >= 0:
        Q[prev_t, town] = Q[prev_t, town] + eta * (reward - Q[prev_t, town] + gamma * Q[town, next_t])
    else:
        Q[prev_t, town] = Q[prev_t, town] - eta * Q[prev_t, town]
        
    return normalize_pi(Q)

このようにすることで、目的地で得られた報酬が、目的地の手前のほうの行動の選択に影響を及ぼすようにします。ゲームオーバーになったときの「負の報酬」も、そこに到るまでの過去の行動の選択に負の影響を及ぼすようにします。

def explore_epsilon_greedy(Q, epsilon=0.1, eta=0.1, gamma=0.9, start=0, goal=46, min_epsilon=0.01):
    epsilon = max(epsilon, min_epsilon)
    route = [start]
    town = get_next(start, Q, epsilon)
    prev_t = start
    while True:
        if town in route:
            reward = -1
            Q = sarsa(town, Q, prev_t, next_t, reward, eta, gamma)
            break
        elif town == goal:
            reward = 1
            route.append(town)
            Q = sarsa(town, Q, prev_t, next_t, reward, eta, gamma)
            break
        else:
            reward = 0
            route.append(town)
            next_t = get_next(town, Q, epsilon)
            Q = sarsa(town, Q, prev_t, next_t, reward, eta, gamma)
            prev_t = town
            town = next_t
    
    return [route, Q]

探索実行

では、探索を開始しましょう。

%%time
eta = 0.1 # 学習率
gamma = 0.9 # 時間割引率
epsilon = 0.5
Q = Q_zero.copy()

best_dist_goal = 1000000
best_len_route = 1000000

best_route2 = []
dist_goal_history2 = []
len_route_history2 = []
for itera in range(50000):
    epsilon = epsilon * 0.99
    route, Q = explore_epsilon_greedy(Q, epsilon, eta, gamma)
    dist_goal, len_route = evaluate(route)
    dist_goal_history2.append(dist_goal)
    len_route_history2.append(len_route)

    if is_best_ever():
        best_dist_goal = dist_goal
        best_len_route = len_route
        best_route2 = route

CPU times: user 7min 50s, sys: 948 ms, total: 7min 50s
Wall time: 7min 53s

探索結果

Epsilon-Greedy法による探索結果の一例です。実は、結果はあまり安定せず、実行するたびに結果がけっこう大きく変わります（試してみてください）。

まずはdist_goalとlen_routeの分布

draw_histgrams(dist_goal_history2, len_route_history2)

dist_goalとlen_routeの関係

draw_scatter(dist_goal_history2, len_route_history2) 

dist_goalの履歴

学習率 eta を大きくすると収束が早くなりますが、局所解に陥る可能性が高くなります。小さくすると、収束は遅くなりますが、局所解に陥る可能性は低くなります。

visualize_history(dist_goal_history2)

dist_goalの履歴の最初の５０００回

visualize_history(dist_goal_history2[:5000])

len_routeの履歴

visualize_history(len_route_history2)

len_routeの履歴の最初の５０００回

visualize_history(len_route_history2[:5000])

Epsilon-Greedy法により得られた最短経路

ここでも、真の最短経路とは少し違う、惜しい結果になりました。方策勾配法で得られた結果と比べてみてください。

draw_route(best_route2)

方策勾配法では、目的地である那覇までの距離をpi値の更新に用いていたため、「目標１：ゴールにたどり着く」と「目標２：最短経路を発見する」を同時に満たす経路を学習していました。このため、何度実行しても、最短経路に近い結果が得られます。

今回のEpsilon-Greedy法では、与えた「報酬」は「ゴールにたどり着いたかどうか」と「ゲームオーバーになったか（同じ都市を二度訪問してしまったか）」だけを反映しています。そのため、「目標１：ゴールにたどり着く」ための方法は学習しますが、「目標２：最短経路を発見する」ための学習はしません。このため、最短経路に近い結果がたまたま得られることはありますが、最短経路とは程遠い結果に収束することも実は多いのです（試してみてください）。

「目標２：最短経路を発見する」ための学習もEpsilon-Greedy法で行えるようにはどうすればよいか、ぜひ考えてみましょう（ここでは取り扱いません）。

Epsilon-Greedy法で学習後のQ値をQ_egとして保存します。

Q_eg = Q.copy()

その値は次のようになります。

visualize_matrix(pd.DataFrame(Q_eg, columns=location[:, 0]))

方策勾配法により得られたpi_pgと比較してみましょう。

Q学習

価値反復法のもうひとつの方法として、「Q学習」(Q-learning)が有名です。基本的には Epsilon-Greedy 法と似ていますが、大きな違いは、「次の行動」を選択するときに生じるランダム性が入らないことです。その分、収束が早くなると言われています。

ですが、私が以下のコードを何度か実行した限りでは、収束が早くなることはありますが必ずそうなるわけでもなく、局所解に陥る（目的地である那覇にたどり着けない）ことが多くなってしまう印象があります。

def Q_learning(town, Q, prev_t, reward, eta=0.1, gamma=0.9, goal=46):
    if reward == 1: #dist_mat[town, goal] == 0:
        Q[prev_t, town] = Q[prev_t, town] + eta * (reward - Q[prev_t, town])
    elif reward >= 0:
        Q[prev_t, town] = Q[prev_t, town] + eta * (reward - Q[prev_t, town] + gamma * np.nanmax(Q[town, :]))
    else:
        Q[prev_t, town] = Q[prev_t, town] - eta * Q[prev_t, town]
        
    return normalize_pi(Q)

def explore_Q_learning(Q, epsilon=0.1, eta=0.1, gamma=0.9, start=0, goal=46):
    prev_t = start
    route = [start]
    town = get_next(start, Q, epsilon)
    while True:
        if town in route:
            reward = -1
            Q = Q_learning(town, Q, prev_t, reward, eta, gamma)
            break
        elif town == goal:
            reward = 1 
            route.append(town)
            Q = Q_learning(town, Q, prev_t, reward, eta, gamma)
            break
        else:
            reward = 0
            dist_goal, len_route = evaluate(route)
            if best_dist_goal > dist_goal:
                reward = 1
            route.append(town)
            next_t = get_next(town, Q, epsilon)
            Q = Q_learning(town, Q, prev_t, reward, eta, gamma)
            prev_t = town
            town = next_t
    
    return [route, Q]

探索実行

%%time
eta = 0.1 # 学習率
gamma = 0.9 # 時間割引率
epsilon = 0.5
Q = Q_zero.copy()

best_dist_goal = 1000000
best_len_route = 1000000

best_route3 = []
dist_goal_history3 = []
len_route_history3 = []
for itera in range(50000):
    epsilon = epsilon * 0.99
    route, Q = explore_Q_learning(Q, epsilon, eta, gamma)
    dist_goal, len_route = evaluate(route)
    dist_goal_history3.append(dist_goal)
    len_route_history3.append(len_route)

    if is_best_ever():
        best_dist_goal = dist_goal
        best_len_route = len_route
        best_route3 = route

CPU times: user 9min 50s, sys: 1.41 s, total: 9min 52s
Wall time: 9min 54s

探索結果

Q学習による探索結果の一例です。Epsilon-Greedy法と同様、結果はあまり安定せず、実行するたびに結果がけっこう大きく変わります（試してみてください）。

dist_goal と len_route の分布

draw_histgrams(dist_goal_history3, len_route_history3)

dist_goal と len_route の関係

draw_scatter(dist_goal_history3, len_route_history3) 

dist_goalの履歴

visualize_history(dist_goal_history3)

dist_goalの履歴の最初の５０００回

visualize_history(dist_goal_history3[:5000])

len_routeの履歴

visualize_history(len_route_history3)

len_routeの履歴の最初の５０００回

visualize_history(len_route_history3[:5000])

Q学習によりにより得られた最短経路

draw_route(best_route3)

この計算例ではっきり分かるように、これは真の最短経路とは異なります。理由は、Epsilon-Greedy法の時に述べたのと同様、「報酬」の設計の問題上、「目標１：ゴールにたどり着く」ための学習は行なっているが、「目標２：最短経路を発見する」ための学習は行なっていないためです。

また上に述べたように、私の観測範囲内において、Q学習は収束が早くなることはあるかも知れませんが、５万回計算しても目的地の那覇にたどり着かないことも多く、「Q学習により得られた最短経路」は「Epsilon-Greedy法により得られた最短経路」より長くなってしまう傾向があるように思います。理由は、「次の行動」を選択するときのランダム性を抑えてあるため、たまたま選んだ経路でゴールまでたどり着いた場合、その経路が長いものであっても、それが変更される機会がEpsilon-Greedy法と比べて少なくなってしまうからではないかと思います。

Q_qlearn = Q.copy()

visualize_matrix(pd.DataFrame(Q_qlearn, columns=location[:, 0]))

と、いうわけで。強化学習については以上です。いやあ、沖縄は遠い。

これに深層学習をミックスした深層強化学習というものがありますが、それはまた別の機会に。チャオ。