CNTK 2.2 Python API 解説 (4) - GAN, DCGAN 画像生成モデルの実装

#CNTK 2.2 Python API 解説 (4) - GAN, DCGAN 画像生成モデルの実装

##0. はじめに

◆ CNTK ( Microsoft Cognitive Toolkit ) 2.2 の Python API 解説第４弾です。
GAN, DCGAN 画像生成モデルを CNTK で実装します。題材は MNIST と Fashion-MNIST を利用します。

生成モデルは この OpenAI ブログ投稿 のように深層学習コミュニティにおいて多くの注意を引いてきました。
現実世界の観測を模倣する現実的なコンテンツ (画像、音 etc.) を生成可能なモデルを作成することは挑戦的な課題ですが、
Generative Adversarial Network (GAN) - 敵対的生成ネットワーク - は有望なアプローチの一つです。
ご存知のように、Yann LeCun からの Quora の引用 は GAN とそのバリエーションを最近 10 年で最も重要なアイデアとしてサマライズされています。

オリジナルのアイデアが Generative Adversarial Nets (Goodfellow et al at NIPS 2014) として発表された後、様々なバリエーションが公開されてきましたが、その中では特に Deep Convolutional Generative Adversarial Network (DCGAN) が推奨される開始点ともなっています。

本記事ではこれらのオリジナルの GAN と DCGAN モデルを CNTK で忠実に実装しています。

本記事の内容 :

1. 動作環境と Jupyter Notebook について
2. 基本 GAN
3. Fashion-MNIST データセットの利用
4. DCGAN

本記事は以下の CNTK チュートリアルを参考にしています :

• CNTK 206: Part A - Basic GAN with MNIST data
• CNTK 206: Part B - Deep Convolutional GAN with MNIST data
• CNTK 103: Part A - MNIST Data Loader

1. 動作環境と Jupyter Notebook について

動作環境

動作環境の構築が必要な場合には、Cognitive Toolkit 2.2 を Azure Linux GPU 仮想マシンにインストール を参考にしてください。Azure ポータルと Ubuntu Linux にある程度慣れていれば、30 分程度で以下のような環境が構築できるかと思います :

• Azure NC 仮想マシン with NVIDIA Tesla® K80 GPU
• Ubuntu 16.04 LTS
• NVIDIA CUDA 8.0 & cuDNN 6.0
• Anaconda 3 4.1.1
• CNTK 2.2 (for GPU)

Jupyter Notebook

また、本記事でも CNTK チュートリアルでも Jupyter Notebook を多用します。
Jupyter Notebook の利用方法については「CNTK 2.2 Python API 入門 (2)」の記事中の Jupyter Notebook の活用 を参照してください。

##2. 基本 GAN

###2-1 概要

生成モデル (Generative models) は この OpenAI ブログ投稿 のように深層学習コミュニティにおいて多くの注意を引いてきました。そして伝統的に半教師 (= semi-supervised) ありと教師なし学習のための識別モデル (Discriminative models) を活用してきました。

生成モデリングの基本的なアイデアは (写真、音声、単語 etc.のような) 興味あるドメインの大量のデータを集めて
そのような現実世界のデータセットを生成するような訓練されたモデルを見出すことです。
これはトレーニングをスケールアップするためのメカニズムを必要とし巨大なデータセットを持つような研究の活発なエリアです。
上のブログ記事でも述べられているように、そのようなアプローチはコンピュータ支援アート生成を遂行するためや、
"make my smile wider" のような何某かの単語による説明へ画像のモーフィングを行なうために使用されるかもしれません。
このアプローチは、画像ノイズ除去、画像修復、超解像技術 (= super-resolution)、構造化予測 (= structured prediction), 強化学習における探索、そしてラベルデータが高価であるような場合のニューラルネットワーク事前トレーニングにおける活用を見出しました。

現実世界の観測を模倣する現実的なコンテンツ (画像、音 etc.) を生成可能なモデルを生成することは挑戦的な課題です。
Generative Adversarial Network (GAN) - 敵対的生成ネットワークは有望なアプローチの一つです。
Yann LeCun からの Quora の引用 によれば、GAN とそのバリエーションを最近 10 年で最も重要なアイデアとして要約しています。
元のアイデアは Generative Adversarial Nets (Goodfellow et al) at NIPS 2014 で提案されています。

◆ 本記事では、合成の MNIST 数字を生成するための基本的な GAN ネットワークを作成するために CNTK をどのように使用するかを示します。

最初に必要なコンポーネントをインポートしましょう。

※ Jupyter Notebook の利用を想定しています。新しい Notebook を作成してください。

In_[1]==>

from IPython.display import Image

In_[2]==>

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os

import cntk as C
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env() # (only needed for our build system)
C.cntk_py.set_fixed_random_seed(1) # fix a random seed for CNTK components

%matplotlib inline

便宜上、２つの実行モードがあります :

• Fast モード: isFast を True に設定します。デフォルト・モードで、より少ない反復で訓練するか限定されたデータで訓練/テストすることを意味します。これは機能的な正当性という意味では確かなものですが、生成されたモデルは完全な訓練によって生成されたものからはかけ離れています。

• Slow モード: 実装に精通した後、異なるパラメータ等でより長い時間、訓練を実行することで洞察を得ることを望むのであれば、このフラグを False に設定してください。

In_[3]==>

isFast = True

※ Azure NC 仮想マシンのように、NVIDIA Tesla K80 GPU 装備であれば Slow モードでもさほど時間はかかりません。

###2-2 データ・リーディング

GAN への入力はランダム数のベクトルです。
また、トレーニングの最後に、GAN は MNIST データベース から描かれた手書き数字の画像を生成することを "学習" します。

以下の記事で生成された CTF フォーマットの MNIST データセットを使用します :

CNTK 2.2 Python API 入門 (3) - MNIST 総集編
2. MNIST データセットを CNTK CTF フォーマットでセーブする

データフォーマットやリーディング方法の詳細は上の記事で見つかりますが、
本記事の目的のためには create_reader 関数が、MNIST データセットから画像を生成するために使用されるオブジェクトを返すことを知っていれば十分です。
教師なしモデルを構築していますので、features を読み込むことだけが必要で、labels は無視されます。

In_[4]==>

# 訓練データが生成されて利用可能であることを確認します。

data_found = False
for data_dir in [os.path.join("..", "Examples", "Image", "DataSets", "MNIST"),
                 os.path.join("data", "MNIST")]:
    train_file = os.path.join(data_dir, "Train-28x28_cntk_text.txt")
    if os.path.isfile(train_file):
        data_found = True
        break
        
if not data_found:
    raise ValueError("Please generate the data by completing CNTK 103 Part A")
    
print("Data directory is {0}".format(data_dir))

Data directory is data/MNIST

リーダーを作成する create_reader() を定義します :

In_[5]==>

def create_reader(path, is_training, input_dim, label_dim):
    deserializer = C.io.CTFDeserializer(
        filename = path,
        streams = C.io.StreamDefs(
            labels_unused = C.io.StreamDef(field = 'labels', shape = label_dim, is_sparse = False),
            features = C.io.StreamDef(field = 'features', shape = input_dim, is_sparse = False
            )
        )
    )
    return C.io.MinibatchSource(
        deserializers = deserializer,
        randomize = is_training,
        max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1
    )

GAN をトレーニングするために使用されるランダム・ノイズは、
区間 [-1, 1] 内の一様分布分布からのランダム・ノイズ・サンプルを生成するための noise_sample 関数で提供されます :

In_[6]==>

np.random.seed(123)
def noise_sample(num_samples):
    return np.random.uniform(
        low = -1.0,
        high = 1.0,
        size = [num_samples, g_input_dim]        
    ).astype(np.float32)

###2-3 モデル作成

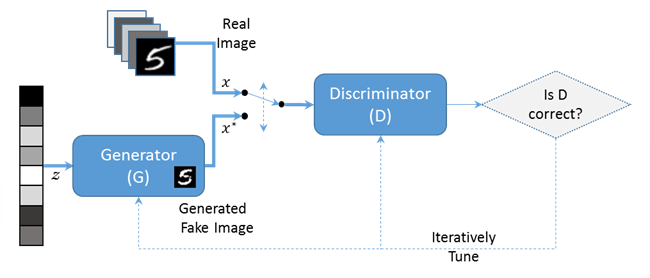
GAN ネットワークは２つのサブネットワークで構成されています、一つは Generator ($G$) と呼ばれ、他方は Discriminator ($D$) です。
※ Generator、Discriminator の訳語としてはそれぞれ生成器、識別器 (or 判別器) が考えられますが、
必ずしも定着しているとは言えませんので英語の術語のままで通すことにします。

• Generator は入力としてランダムノイズ・ベクトル ($z$) を取り、
  そして MNIST データセットからの本物の (= real) 画像 ($x$) と見分けがつかないような偽物 (= fake) 画像 ($x^*$) を出力しようとします。

• Discriminator は本物画像 ($x$) と偽物画像 ($x^*$) の間を識別しようとします。

In_[7]==>

Image(url="https://www.cntk.ai/jup/GAN_basic_flow.png")

各トレーニング反復において、Generator はより本物に近い (= realistic) 偽物画像を生成します。
換言すれば、本物と生成された対照物の間の違いを 最小化 します。

そしてまた Discriminator は (訓練セットからの) 本物のサンプルと生成された偽物の両者に正しいラベル (real vs. fake) を割り当てる確率を 最大化 します。

サブネットワーク ($G$ と $D$) 間の２つの相反する目的(群)は GAN ネットワークを (訓練されたときに) 均衡に収束することへ導きます。そこでは Generator は本物に見える偽物の MNIST 画像を生成して、Discriminator は画像が本物か偽物かを推測できます (生成画像がベストケースでは無作為になるでしょう)。
そして訓練された結果としての Generator モデルは、ランダム数である入力から本物らしく見える MNIST 画像を生成します。

####モデリング

モデルのための計算グラフを構築します、generator と discriminator 各々のために一つです。
最初に、モデルのアーキテクチャ的なそして訓練用のハイパーパラメータの幾つかを設定します。

Generator

• generator ネットワークは単一の隠れ層を持つ完全結合ネットワークです。つまり２つの Dense 層で単純なモデル化をします。

• 入力として 100-次元のランダムベクトルを取ります。

• 出力は 784 次元ベクトルで、これは偽物の 28 x 28 (合成) 画像 ($x^*$) の平坦化されたバージョンに相当します。

• generator 関数の出力が区間 [-1, 1] に収まるように最終層で tanh 活性化を使用します。
  これは必須で、何故ならば MNIST 画像もまたこの区間にスケールされているからです。

Discriminator

• discriminator もまた単一の隠れ層を持つ完全結合ネットワークで、２つの Dense 層でモデル化します。

• 入力として generator の 784 次元出力か本物の MNIST 画像を取ります。

• 出力は単一のスカラーで、これは入力画像が本物の MNIST 画像であると見積もられた確率です。

• 最終層は確率を生成するための sigmoid 活性です。

In_[8]==>

# architectural parameters
g_input_dim = 100
g_hidden_dim = 128
g_output_dim = d_input_dim = 784
d_hidden_dim = 128
d_output_dim = 1

In_[9]==>

def generator(z):
    with C.layers.default_options(init = C.xavier()):
        h1 = C.layers.Dense(g_hidden_dim, activation = C.relu)(z)
        return C.layers.Dense(g_output_dim, activation = C.tanh)(h1)

In_[10]==>

def discriminator(x):
    with C.layers.default_options(init = C.xavier()):
        h1 = C.layers.Dense(d_hidden_dim, activation = C.relu)(x)
        return C.layers.Dense(d_output_dim, activation = C.sigmoid)(h1)

◆ トレーニングのために、ミニバッチサイズ 1024 と固定された学習率 0.0005 を使用します。
また、Fast モードでは 300 反復のみで機能的な正当性を検証することになります :

In_[11]==>

# training config
minibatch_size = 1024
num_minibatches = 300 if isFast else 40000
lr = 0.00005

※ isFast フラグは num_minibatches の設定値を切り替えるだけです。GPU 環境によって num_minibatches を加減しましょう。

###2-4 グラフを構築する

計算グラフの残りの殆どは、訓練アルゴリズムとパラメータ更新をコーディネートするためのものです。
それは GAN に関連する 2, 3 の理由のために幾分トリッキーです :

• 第一に、discriminator は本物の MNIST 画像と generator 関数で生成された偽物の画像の両者の上で使用されなければなりません。計算グラフでこれを表わす一つの方法は、代替入力だけを別に使用して discriminator 関数の出力のクローンを作成することです。
  clone 関数で method=share を設定すれば、discriminator モデルを通した両者のパスがパラメータの同じセットを使用することを保証します。

• ２番目に、generator と discriminator モデルのために異なる損失関数からの勾配を使用して別々にパラメータを更新する必要があります。
  グラフの Function のためのパラメータを parameters 属性で得ることができます。
  けれども、モデルパラメータを更新するとき、それぞれのモデルのパラメータだけを更新します。その一方で他方のパラメータは変更されないまま保持されます。換言すれば、generator を更新するとき $G$ 関数のパラメータだけを更新します。その一方で $D$ 関数のパラメータは固定されたまま保持します。そして反対もまた同様です。

In_[12]==>

def build_graph(noise_shape, image_shape,
                G_progress_printer, D_progress_printer):
    input_dynamic_axes = [C.Axis.default_batch_axis()]
    Z = C.input_variable(noise_shape, dynamic_axes=input_dynamic_axes)
    X_real = C.input_variable(image_shape, dynamic_axes=input_dynamic_axes)
    X_real_scaled = 2*(X_real / 255.0) - 1.0

    # generator と discriminator モデルのためのモデル関数を作成します。
    X_fake = generator(Z)
    D_real = discriminator(X_real_scaled)
    # discriminator のクローンを作成します。
    D_fake = D_real.clone(
        method = 'share',
        substitutions = {X_real_scaled.output: X_fake.output}
    )

    # 損失関数を作成して最適化アルゴリズムを構成します。
    G_loss = 1.0 - C.log(D_fake)
    D_loss = -(C.log(D_real) + C.log(1.0 - D_fake))

    G_learner = C.fsadagrad(
        parameters = X_fake.parameters,
        lr = C.learning_rate_schedule(lr, C.UnitType.sample),
        momentum = C.momentum_as_time_constant_schedule(700)
    )
    D_learner = C.fsadagrad(
        parameters = D_real.parameters,
        lr = C.learning_rate_schedule(lr, C.UnitType.sample),
        momentum = C.momentum_as_time_constant_schedule(700)
    )

    # trainer をインスタンス化します。
    G_trainer = C.Trainer(
        X_fake,
        (G_loss, None),
        G_learner,
        G_progress_printer
    )
    D_trainer = C.Trainer(
        D_real,
        (D_loss, None),
        D_learner,
        D_progress_printer
    )

    return X_real, X_fake, Z, G_trainer, D_trainer

###2-5 モデルをトレーニングする

GAN のトレーニングのためのコードは NIPS 2014 原論文 で表された時のアルゴリズムを極めて忠実にフォローしています。
この実装では、トレーニング・サンプルと $G$ からのサンプルの両者に正しいラベル (fake vs. real) を割り当てる確率を最大化するために $D$ をトレーニングします。
換言すれば、$D$ と $G$ は次の価値関数 (= value function) $V(G,D)$ を持つ２人プレーヤーのミニマックス・ゲームをプレーします :

\min_G \max_D V(D,G)= \mathbb{E}_{x}[ log D(x) ] + \mathbb{E}_{z}[ log(1 - D(G(z))) ]

このゲームの最適点 (= optimal point) では、generator は本物に見えるデータを生成し、
その一方で discriminator は生成された画像がまさに 0.5 の確率で偽物であることを予測するでしょう。

原論文 からの以下のアルゴリズムが実装されています :

In_[13]==>

Image(url="https://www.cntk.ai/jup/GAN_goodfellow_NIPS2014.png", width = 500)

定義された価値関数で GAN モデルをトレーニングすることを進めます :

In_[14]==>

def train(reader_train):
    k = 2
    
    # print out loss for each model for upto 50 times
    print_frequency_mbsize = num_minibatches // 50
    pp_G = C.logging.ProgressPrinter(print_frequency_mbsize)
    pp_D = C.logging.ProgressPrinter(print_frequency_mbsize * k)

    X_real, X_fake, Z, G_trainer, D_trainer = \
        build_graph(g_input_dim, d_input_dim, pp_G, pp_D)
    
    input_map = {X_real: reader_train.streams.features}
    for train_step in range(num_minibatches):

        # k steps のために discriminator モデルをトレーニングします。
        for gen_train_step in range(k):
            Z_data = noise_sample(minibatch_size)
            X_data = reader_train.next_minibatch(minibatch_size, input_map)
            if X_data[X_real].num_samples == Z_data.shape[0]:
                batch_inputs = {X_real: X_data[X_real].data, 
                                Z: Z_data}
                D_trainer.train_minibatch(batch_inputs)

        # 単一のステップのために generator モデルをトレーニングします。
        Z_data = noise_sample(minibatch_size)
        batch_inputs = {Z: Z_data}
        G_trainer.train_minibatch(batch_inputs)

        G_trainer_loss = G_trainer.previous_minibatch_loss_average

    return Z, X_fake, G_trainer_loss

◆ トレーニングを実行します :

In_[15]==>

%%time
reader_train = create_reader(train_file, True, d_input_dim, label_dim=10)

G_input, G_output, G_trainer_loss = train(reader_train)

Learning rate per 1 samples: 5e-05
Learning rate per 1 samples: 5e-05
 Minibatch[   1-  12]: loss = 0.462199 * 12288, metric = 0.00% * 12288;
 Minibatch[   1-   6]: loss = 2.740121 * 6144, metric = 0.00% * 6144;
 Minibatch[  13-  24]: loss = 0.496172 * 12288, metric = 0.00% * 12288;
 Minibatch[   7-  12]: loss = 2.405166 * 6144, metric = 0.00% * 6144;
 Minibatch[  25-  36]: loss = 0.467010 * 12288, metric = 0.00% * 12288;
 Minibatch[  13-  18]: loss = 2.497321 * 6144, metric = 0.00% * 6144;
 Minibatch[  37-  48]: loss = 0.578210 * 12288, metric = 0.00% * 12288;
 Minibatch[  19-  24]: loss = 2.668613 * 6144, metric = 0.00% * 6144;
 Minibatch[  49-  60]: loss = 1.253507 * 12288, metric = 0.00% * 12288;
 Minibatch[  25-  30]: loss = 2.147166 * 6144, metric = 0.00% * 6144;
 Minibatch[  61-  72]: loss = 1.200059 * 12288, metric = 0.00% * 12288;
 Minibatch[  31-  36]: loss = 1.767957 * 6144, metric = 0.00% * 6144;
 Minibatch[  73-  84]: loss = 1.000537 * 12288, metric = 0.00% * 12288;
 Minibatch[  37-  42]: loss = 1.953677 * 6144, metric = 0.00% * 6144;
 Minibatch[  85-  96]: loss = 0.992998 * 12288, metric = 0.00% * 12288;
 Minibatch[  43-  48]: loss = 1.907767 * 6144, metric = 0.00% * 6144;
 Minibatch[  97- 108]: loss = 1.095865 * 12288, metric = 0.00% * 12288;
 Minibatch[  49-  54]: loss = 1.885712 * 6144, metric = 0.00% * 6144;
 Minibatch[ 109- 120]: loss = 0.914263 * 12288, metric = 0.00% * 12288;
 Minibatch[  55-  60]: loss = 2.034668 * 6144, metric = 0.00% * 6144;
 Minibatch[ 121- 132]: loss = 0.981053 * 12288, metric = 0.00% * 12288;
 Minibatch[  61-  66]: loss = 1.681572 * 6144, metric = 0.00% * 6144;
 Minibatch[ 133- 144]: loss = 0.986912 * 12288, metric = 0.00% * 12288;
 Minibatch[  67-  72]: loss = 2.140551 * 6144, metric = 0.00% * 6144;
 Minibatch[ 145- 156]: loss = 1.029776 * 12288, metric = 0.00% * 12288;
 Minibatch[  73-  78]: loss = 2.222153 * 6144, metric = 0.00% * 6144;
 Minibatch[ 157- 168]: loss = 1.074163 * 12288, metric = 0.00% * 12288;
 Minibatch[  79-  84]: loss = 1.874583 * 6144, metric = 0.00% * 6144;
 Minibatch[ 169- 180]: loss = 1.012319 * 12288, metric = 0.00% * 12288;
 Minibatch[  85-  90]: loss = 2.160492 * 6144, metric = 0.00% * 6144;
 Minibatch[ 181- 192]: loss = 1.046508 * 12288, metric = 0.00% * 12288;
 Minibatch[  91-  96]: loss = 2.145467 * 6144, metric = 0.00% * 6144;
 Minibatch[ 193- 204]: loss = 0.998191 * 12288, metric = 0.00% * 12288;
 Minibatch[  97- 102]: loss = 1.971995 * 6144, metric = 0.00% * 6144;
 Minibatch[ 205- 216]: loss = 0.871338 * 12288, metric = 0.00% * 12288;
 Minibatch[ 103- 108]: loss = 2.242180 * 6144, metric = 0.00% * 6144;
 Minibatch[ 217- 228]: loss = 0.886368 * 12288, metric = 0.00% * 12288;
 Minibatch[ 109- 114]: loss = 1.999341 * 6144, metric = 0.00% * 6144;
 Minibatch[ 229- 240]: loss = 0.765167 * 12288, metric = 0.00% * 12288;
 Minibatch[ 115- 120]: loss = 1.963046 * 6144, metric = 0.00% * 6144;
 Minibatch[ 241- 252]: loss = 0.701160 * 12288, metric = 0.00% * 12288;
 Minibatch[ 121- 126]: loss = 2.017092 * 6144, metric = 0.00% * 6144;
 Minibatch[ 253- 264]: loss = 0.599012 * 12288, metric = 0.00% * 12288;
 Minibatch[ 127- 132]: loss = 2.145289 * 6144, metric = 0.00% * 6144;
 Minibatch[ 265- 276]: loss = 0.583949 * 12288, metric = 0.00% * 12288;
 Minibatch[ 133- 138]: loss = 2.203003 * 6144, metric = 0.00% * 6144;
 Minibatch[ 277- 288]: loss = 0.540344 * 12288, metric = 0.00% * 12288;
 Minibatch[ 139- 144]: loss = 2.300390 * 6144, metric = 0.00% * 6144;
 Minibatch[ 289- 300]: loss = 0.572188 * 12288, metric = 0.00% * 12288;
 Minibatch[ 145- 150]: loss = 2.235377 * 6144, metric = 0.00% * 6144;
 Minibatch[ 301- 312]: loss = 0.670872 * 12288, metric = 0.00% * 12288;
 Minibatch[ 151- 156]: loss = 2.105199 * 6144, metric = 0.00% * 6144;
 Minibatch[ 313- 324]: loss = 0.771057 * 12288, metric = 0.00% * 12288;
 Minibatch[ 157- 162]: loss = 2.048172 * 6144, metric = 0.00% * 6144;
 Minibatch[ 325- 336]: loss = 0.729266 * 12288, metric = 0.00% * 12288;
 Minibatch[ 163- 168]: loss = 2.099406 * 6144, metric = 0.00% * 6144;
 Minibatch[ 337- 348]: loss = 0.730148 * 12288, metric = 0.00% * 12288;
 Minibatch[ 169- 174]: loss = 2.083410 * 6144, metric = 0.00% * 6144;
 Minibatch[ 349- 360]: loss = 0.725876 * 12288, metric = 0.00% * 12288;
 Minibatch[ 175- 180]: loss = 2.090485 * 6144, metric = 0.00% * 6144;
 Minibatch[ 361- 372]: loss = 0.656270 * 12288, metric = 0.00% * 12288;
 Minibatch[ 181- 186]: loss = 2.146983 * 6144, metric = 0.00% * 6144;
 Minibatch[ 373- 384]: loss = 0.794894 * 12288, metric = 0.00% * 12288;
 Minibatch[ 187- 192]: loss = 2.045507 * 6144, metric = 0.00% * 6144;
 Minibatch[ 385- 396]: loss = 0.780113 * 12288, metric = 0.00% * 12288;
 Minibatch[ 193- 198]: loss = 2.102519 * 6144, metric = 0.00% * 6144;
 Minibatch[ 397- 408]: loss = 0.855189 * 12288, metric = 0.00% * 12288;
 Minibatch[ 199- 204]: loss = 1.906804 * 6144, metric = 0.00% * 6144;
 Minibatch[ 409- 420]: loss = 0.899531 * 12288, metric = 0.00% * 12288;
 Minibatch[ 205- 210]: loss = 1.869400 * 6144, metric = 0.00% * 6144;
 Minibatch[ 421- 432]: loss = 0.839877 * 12288, metric = 0.00% * 12288;
 Minibatch[ 211- 216]: loss = 1.996490 * 6144, metric = 0.00% * 6144;
 Minibatch[ 433- 444]: loss = 0.892059 * 12288, metric = 0.00% * 12288;
 Minibatch[ 217- 222]: loss = 1.855209 * 6144, metric = 0.00% * 6144;
 Minibatch[ 445- 456]: loss = 0.937429 * 12288, metric = 0.00% * 12288;
 Minibatch[ 223- 228]: loss = 1.925410 * 6144, metric = 0.00% * 6144;
 Minibatch[ 457- 468]: loss = 0.804530 * 12288, metric = 0.00% * 12288;
 Minibatch[ 229- 234]: loss = 2.007807 * 6144, metric = 0.00% * 6144;
 Minibatch[ 469- 480]: loss = 0.807353 * 12288, metric = 0.00% * 12288;
 Minibatch[ 235- 240]: loss = 1.913325 * 6144, metric = 0.00% * 6144;
 Minibatch[ 481- 492]: loss = 0.843374 * 12288, metric = 0.00% * 12288;
 Minibatch[ 241- 246]: loss = 2.056712 * 6144, metric = 0.00% * 6144;
 Minibatch[ 493- 504]: loss = 0.750913 * 12288, metric = 0.00% * 12288;
 Minibatch[ 247- 252]: loss = 2.096425 * 6144, metric = 0.00% * 6144;
 Minibatch[ 505- 516]: loss = 0.785370 * 12288, metric = 0.00% * 12288;
 Minibatch[ 253- 258]: loss = 1.928477 * 6144, metric = 0.00% * 6144;
 Minibatch[ 517- 528]: loss = 0.754743 * 12288, metric = 0.00% * 12288;
 Minibatch[ 259- 264]: loss = 2.090953 * 6144, metric = 0.00% * 6144;
 Minibatch[ 529- 540]: loss = 0.822744 * 12288, metric = 0.00% * 12288;
 Minibatch[ 265- 270]: loss = 1.943075 * 6144, metric = 0.00% * 6144;
 Minibatch[ 541- 552]: loss = 0.773524 * 12288, metric = 0.00% * 12288;
 Minibatch[ 271- 276]: loss = 2.073863 * 6144, metric = 0.00% * 6144;
 Minibatch[ 553- 564]: loss = 0.777265 * 12288, metric = 0.00% * 12288;
 Minibatch[ 277- 282]: loss = 1.996480 * 6144, metric = 0.00% * 6144;
 Minibatch[ 565- 576]: loss = 0.748617 * 12288, metric = 0.00% * 12288;
 Minibatch[ 283- 288]: loss = 2.033824 * 6144, metric = 0.00% * 6144;
 Minibatch[ 577- 588]: loss = 0.727727 * 12288, metric = 0.00% * 12288;
 Minibatch[ 289- 294]: loss = 2.043813 * 6144, metric = 0.00% * 6144;
 Minibatch[ 589- 600]: loss = 0.727470 * 12288, metric = 0.00% * 12288;
 Minibatch[ 295- 300]: loss = 1.993225 * 6144, metric = 0.00% * 6144;
CPU times: user 6.1 s, sys: 4.52 s, total: 10.6 s
Wall time: 9.4 s

In_[16]==>

# generator 損失を表示出力します。
print("Training loss of the generator is: {0:.2f}".format(G_trainer_loss))

Training loss of the generator is: 1.87

偽物の (合成) 画像を生成する

モデルのトレーニングが完了したので、generator にランダム・ノイズを供給しすることにより、偽物の画像を作成できます。
サンプルの新しいセットを取得するためには、セルを再実行すれば良いです :

In_[17]==>

def plot_images(images, subplot_shape):
    plt.style.use('ggplot')
    fig, axes = plt.subplots(*subplot_shape)
    for image, ax in zip(images, axes.flatten()):
        ax.imshow(image.reshape(28, 28), vmin = 0, vmax = 1.0, cmap = 'gray')
        ax.axis('off')
    plt.show()
    
noise = noise_sample(36)
images = G_output.eval({G_input: noise})
plot_images(images, subplot_shape =[6, 6])

上のサンプル画像は、Fast モードでトレーニングしたモデルを使用しています。トレーニングが不足しているようです。

より大きな反復数はより本物に見える MNIST 画像を生成するでしょう。そのようにして生成された画像の例は以下で示されます :

In_[18]==>

Image(url="http://www.cntk.ai/jup/GAN_basic_slowmode.jpg")

##3. Fashion-MNIST データセットの利用

次に、MNIST よりも難易度が高い Fashion-MNIST で基本 GAN を試してみましょう。
以下の記事で作成したデータセットをそのまま再利用します :

CNTK 2.2 Python API 入門 (6) - <総集編> Fashion-MNIST データセットの活用
2. Fashion-MNIST データセットとは / 前処理 (CTF ファイルへセーブ)

インポートから始めます。Jupyter Notebook の新しいノートを作成してください :

In_[1]==>

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os

import cntk as C
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env() # (only needed for our build system)
C.cntk_py.set_fixed_random_seed(1) # fix a random seed for CNTK components

%matplotlib inline

Fashion-MNIST の場合には Fast モードではトレーニングが不十分となりますので、Slow モードを選択します :

In_[2]==>

isFast = False
#isFast = True

データセットの存在を確認します :

In_[3]==>

# 訓練データが生成されて利用可能であることを確認します。

data_found = False
for data_dir in [os.path.join("data", "FASHION")]:
    train_file = os.path.join(data_dir, "Train-28x28_cntk_text.fashion.txt")
    if os.path.isfile(train_file):
        data_found = True
        break

if not data_found:
    raise ValueError("Please generate the data by completing CNTK 103 Part A")

print("Data directory is {0}".format(data_dir))

Data directory is data/FASHION

データリーダーを作成します :

In_[4]==>

def create_reader(path, is_training, input_dim, label_dim):
    deserializer = C.io.CTFDeserializer(
        filename = path,
        streams = C.io.StreamDefs(
            labels_unused = C.io.StreamDef(field = 'labels', shape = label_dim, is_sparse = False),
            features = C.io.StreamDef(field = 'features', shape = input_dim, is_sparse = False
            )
        )
    )
    return C.io.MinibatchSource(
        deserializers = deserializer,
        randomize = is_training,
        max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1
    )

In_[5]==>

np.random.seed(123)
def noise_sample(num_samples):
    return np.random.uniform(
        low = -1.0,
        high = 1.0,
        size = [num_samples, g_input_dim]        
    ).astype(np.float32)

前章と完全に同一なモデルを使用します :

In_[6]==>

# architectural parameters
g_input_dim = 100
g_hidden_dim = 128
g_output_dim = d_input_dim = 784
d_hidden_dim = 128
d_output_dim = 1

def generator(z):
    with C.layers.default_options(init = C.xavier()):
        h1 = C.layers.Dense(g_hidden_dim, activation = C.relu)(z)
        return C.layers.Dense(g_output_dim, activation = C.tanh)(h1)

def discriminator(x):
    with C.layers.default_options(init = C.xavier()):
        h1 = C.layers.Dense(d_hidden_dim, activation = C.relu)(x)
        return C.layers.Dense(d_output_dim, activation = C.sigmoid)(h1)

In_[7]==>

# training config
minibatch_size = 1024
num_minibatches = 300 if isFast else 40000
lr = 0.00005

In_[8]==>

def build_graph(noise_shape, image_shape,
                G_progress_printer, D_progress_printer):
    input_dynamic_axes = [C.Axis.default_batch_axis()]
    Z = C.input_variable(noise_shape, dynamic_axes=input_dynamic_axes)
    X_real = C.input_variable(image_shape, dynamic_axes=input_dynamic_axes)
    X_real_scaled = 2*(X_real / 255.0) - 1.0

    # generator と discriminator モデルのためのモデル関数を作成します。
    X_fake = generator(Z)
    D_real = discriminator(X_real_scaled)
    # discriminator のクローンを作成します。
    D_fake = D_real.clone(
        method = 'share',
        substitutions = {X_real_scaled.output: X_fake.output}
    )

    # 損失関数を作成して最適化アルゴリズムを構成します。
    G_loss = 1.0 - C.log(D_fake)
    D_loss = -(C.log(D_real) + C.log(1.0 - D_fake))

    G_learner = C.fsadagrad(
        parameters = X_fake.parameters,
        lr = C.learning_rate_schedule(lr, C.UnitType.sample),
        momentum = C.momentum_as_time_constant_schedule(700)
    )
    D_learner = C.fsadagrad(
        parameters = D_real.parameters,
        lr = C.learning_rate_schedule(lr, C.UnitType.sample),
        momentum = C.momentum_as_time_constant_schedule(700)
    )

    # trainer をインスタンス化します。
    G_trainer = C.Trainer(
        X_fake,
        (G_loss, None),
        G_learner,
        G_progress_printer
    )
    D_trainer = C.Trainer(
        D_real,
        (D_loss, None),
        D_learner,
        D_progress_printer
    )

    return X_real, X_fake, Z, G_trainer, D_trainer

トレーニング関数もまったく同じです :

In_[9]==>

def train(reader_train):
    k = 2

    # print out loss for each model for upto 50 times
    print_frequency_mbsize = num_minibatches // 50
    pp_G = C.logging.ProgressPrinter(print_frequency_mbsize)
    pp_D = C.logging.ProgressPrinter(print_frequency_mbsize * k)

    X_real, X_fake, Z, G_trainer, D_trainer = \
        build_graph(g_input_dim, d_input_dim, pp_G, pp_D)

    input_map = {X_real: reader_train.streams.features}
    for train_step in range(num_minibatches):

        # train the discriminator model for k steps
        for gen_train_step in range(k):
            Z_data = noise_sample(minibatch_size)
            X_data = reader_train.next_minibatch(minibatch_size, input_map)
            if X_data[X_real].num_samples == Z_data.shape[0]:
                batch_inputs = {X_real: X_data[X_real].data, 
                                Z: Z_data}
                D_trainer.train_minibatch(batch_inputs)

        # train the generator model for a single step
        Z_data = noise_sample(minibatch_size)
        batch_inputs = {Z: Z_data}
        G_trainer.train_minibatch(batch_inputs)

        G_trainer_loss = G_trainer.previous_minibatch_loss_average

    return Z, X_fake, G_trainer_loss

◆ トレーニングを実行します。Tesla K-80 で 30 分ほどかかります :

In_[10]==>

%%time
reader_train = create_reader(train_file, True, d_input_dim, label_dim=10)

G_input, G_output, G_trainer_loss = train(reader_train)

Learning rate per 1 samples: 5e-05
Learning rate per 1 samples: 5e-05
 Minibatch[   1-1600]: loss = 0.690872 * 1638400, metric = 0.00% * 1638400;
 Minibatch[   1- 800]: loss = 2.377356 * 819200, metric = 0.00% * 819200;
 Minibatch[1601-3200]: loss = 0.764004 * 1638400, metric = 0.00% * 1638400;
 Minibatch[ 801-1600]: loss = 2.481912 * 819200, metric = 0.00% * 819200;
 Minibatch[3201-4800]: loss = 0.823704 * 1638400, metric = 0.00% * 1638400;
 Minibatch[1601-2400]: loss = 2.416702 * 819200, metric = 0.00% * 819200;
 Minibatch[4801-6400]: loss = 0.879532 * 1638400, metric = 0.00% * 1638400;
 Minibatch[2401-3200]: loss = 2.343907 * 819200, metric = 0.00% * 819200;
 Minibatch[6401-8000]: loss = 0.897595 * 1638400, metric = 0.00% * 1638400;
 Minibatch[3201-4000]: loss = 2.326105 * 819200, metric = 0.00% * 819200;
 Minibatch[8001-9600]: loss = 0.918796 * 1638400, metric = 0.00% * 1638400;
 Minibatch[4001-4800]: loss = 2.294905 * 819200, metric = 0.00% * 819200;
 Minibatch[9601-11200]: loss = 0.937824 * 1638400, metric = 0.00% * 1638400;
 Minibatch[4801-5600]: loss = 2.267324 * 819200, metric = 0.00% * 819200;
 Minibatch[11201-12800]: loss = 0.954942 * 1638400, metric = 0.00% * 1638400;
 Minibatch[5601-6400]: loss = 2.254395 * 819200, metric = 0.00% * 819200;
 Minibatch[12801-14400]: loss = 0.946076 * 1638400, metric = 0.00% * 1638400;
 Minibatch[6401-7200]: loss = 2.262751 * 819200, metric = 0.00% * 819200;
 Minibatch[14401-16000]: loss = 0.956516 * 1638400, metric = 0.00% * 1638400;
 Minibatch[7201-8000]: loss = 2.261199 * 819200, metric = 0.00% * 819200;
 Minibatch[16001-17600]: loss = 0.977333 * 1638400, metric = 0.00% * 1638400;
 Minibatch[8001-8800]: loss = 2.226609 * 819200, metric = 0.00% * 819200;
 Minibatch[17601-19200]: loss = 0.982728 * 1638400, metric = 0.00% * 1638400;
 Minibatch[8801-9600]: loss = 2.211472 * 819200, metric = 0.00% * 819200;
 Minibatch[19201-20800]: loss = 0.989845 * 1638400, metric = 0.00% * 1638400;
 Minibatch[9601-10400]: loss = 2.206333 * 819200, metric = 0.00% * 819200;
 Minibatch[20801-22400]: loss = 0.995975 * 1638400, metric = 0.00% * 1638400;
 Minibatch[10401-11200]: loss = 2.206384 * 819200, metric = 0.00% * 819200;
 Minibatch[22401-24000]: loss = 1.000618 * 1638400, metric = 0.00% * 1638400;
 Minibatch[11201-12000]: loss = 2.191179 * 819200, metric = 0.00% * 819200;
 Minibatch[24001-25600]: loss = 1.000966 * 1638400, metric = 0.00% * 1638400;
 Minibatch[12001-12800]: loss = 2.197861 * 819200, metric = 0.00% * 819200;
 Minibatch[25601-27200]: loss = 1.014229 * 1638400, metric = 0.00% * 1638400;
 Minibatch[12801-13600]: loss = 2.169543 * 819200, metric = 0.00% * 819200;
 Minibatch[27201-28800]: loss = 1.019569 * 1638400, metric = 0.00% * 1638400;
 Minibatch[13601-14400]: loss = 2.165371 * 819200, metric = 0.00% * 819200;
 Minibatch[28801-30400]: loss = 1.020371 * 1638400, metric = 0.00% * 1638400;
 Minibatch[14401-15200]: loss = 2.163823 * 819200, metric = 0.00% * 819200;
 Minibatch[30401-32000]: loss = 1.015515 * 1638400, metric = 0.00% * 1638400;
 Minibatch[15201-16000]: loss = 2.167529 * 819200, metric = 0.00% * 819200;
 Minibatch[32001-33600]: loss = 1.011313 * 1638400, metric = 0.00% * 1638400;
 Minibatch[16001-16800]: loss = 2.174614 * 819200, metric = 0.00% * 819200;
 Minibatch[33601-35200]: loss = 1.009371 * 1638400, metric = 0.00% * 1638400;
 Minibatch[16801-17600]: loss = 2.175625 * 819200, metric = 0.00% * 819200;
 Minibatch[35201-36800]: loss = 1.003196 * 1638400, metric = 0.00% * 1638400;
 Minibatch[17601-18400]: loss = 2.188569 * 819200, metric = 0.00% * 819200;
 Minibatch[36801-38400]: loss = 1.012786 * 1638400, metric = 0.00% * 1638400;
 Minibatch[18401-19200]: loss = 2.175386 * 819200, metric = 0.00% * 819200;
 Minibatch[38401-40000]: loss = 1.010688 * 1638400, metric = 0.00% * 1638400;
 Minibatch[19201-20000]: loss = 2.170737 * 819200, metric = 0.00% * 819200;
 Minibatch[40001-41600]: loss = 1.016777 * 1638400, metric = 0.00% * 1638400;
 Minibatch[20001-20800]: loss = 2.163667 * 819200, metric = 0.00% * 819200;
 Minibatch[41601-43200]: loss = 1.020867 * 1638400, metric = 0.00% * 1638400;
 Minibatch[20801-21600]: loss = 2.162554 * 819200, metric = 0.00% * 819200;
 Minibatch[43201-44800]: loss = 1.020186 * 1638400, metric = 0.00% * 1638400;
 Minibatch[21601-22400]: loss = 2.151719 * 819200, metric = 0.00% * 819200;
 Minibatch[44801-46400]: loss = 1.020530 * 1638400, metric = 0.00% * 1638400;
 Minibatch[22401-23200]: loss = 2.151675 * 819200, metric = 0.00% * 819200;
 Minibatch[46401-48000]: loss = 1.026887 * 1638400, metric = 0.00% * 1638400;
 Minibatch[23201-24000]: loss = 2.152085 * 819200, metric = 0.00% * 819200;
 Minibatch[48001-49600]: loss = 1.020540 * 1638400, metric = 0.00% * 1638400;
 Minibatch[24001-24800]: loss = 2.154365 * 819200, metric = 0.00% * 819200;
 Minibatch[49601-51200]: loss = 1.014448 * 1638400, metric = 0.00% * 1638400;
 Minibatch[24801-25600]: loss = 2.165005 * 819200, metric = 0.00% * 819200;
 Minibatch[51201-52800]: loss = 1.015693 * 1638400, metric = 0.00% * 1638400;
 Minibatch[25601-26400]: loss = 2.163726 * 819200, metric = 0.00% * 819200;
 Minibatch[52801-54400]: loss = 1.013967 * 1638400, metric = 0.00% * 1638400;
 Minibatch[26401-27200]: loss = 2.167246 * 819200, metric = 0.00% * 819200;
 Minibatch[54401-56000]: loss = 1.017556 * 1638400, metric = 0.00% * 1638400;
 Minibatch[27201-28000]: loss = 2.157505 * 819200, metric = 0.00% * 819200;
 Minibatch[56001-57600]: loss = 1.015674 * 1638400, metric = 0.00% * 1638400;
 Minibatch[28001-28800]: loss = 2.162871 * 819200, metric = 0.00% * 819200;
 Minibatch[57601-59200]: loss = 1.012131 * 1638400, metric = 0.00% * 1638400;
 Minibatch[28801-29600]: loss = 2.160371 * 819200, metric = 0.00% * 819200;
 Minibatch[59201-60800]: loss = 1.012878 * 1638400, metric = 0.00% * 1638400;
 Minibatch[29601-30400]: loss = 2.167373 * 819200, metric = 0.00% * 819200;
 Minibatch[60801-62400]: loss = 1.012546 * 1638400, metric = 0.00% * 1638400;
 Minibatch[30401-31200]: loss = 2.164482 * 819200, metric = 0.00% * 819200;
 Minibatch[62401-64000]: loss = 1.014312 * 1638400, metric = 0.00% * 1638400;
 Minibatch[31201-32000]: loss = 2.177949 * 819200, metric = 0.00% * 819200;
 Minibatch[64001-65600]: loss = 1.012102 * 1638400, metric = 0.00% * 1638400;
 Minibatch[32001-32800]: loss = 2.171475 * 819200, metric = 0.00% * 819200;
 Minibatch[65601-67200]: loss = 1.004551 * 1638400, metric = 0.00% * 1638400;
 Minibatch[32801-33600]: loss = 2.176348 * 819200, metric = 0.00% * 819200;
 Minibatch[67201-68800]: loss = 1.002266 * 1638400, metric = 0.00% * 1638400;
 Minibatch[33601-34400]: loss = 2.187627 * 819200, metric = 0.00% * 819200;
 Minibatch[68801-70400]: loss = 1.002441 * 1638400, metric = 0.00% * 1638400;
 Minibatch[34401-35200]: loss = 2.182393 * 819200, metric = 0.00% * 819200;
 Minibatch[70401-72000]: loss = 0.997563 * 1638400, metric = 0.00% * 1638400;
 Minibatch[35201-36000]: loss = 2.189648 * 819200, metric = 0.00% * 819200;
 Minibatch[72001-73600]: loss = 0.997988 * 1638400, metric = 0.00% * 1638400;
 Minibatch[36001-36800]: loss = 2.199209 * 819200, metric = 0.00% * 819200;
 Minibatch[73601-75200]: loss = 0.992422 * 1638400, metric = 0.00% * 1638400;
 Minibatch[36801-37600]: loss = 2.197578 * 819200, metric = 0.00% * 819200;
 Minibatch[75201-76800]: loss = 0.991016 * 1638400, metric = 0.00% * 1638400;
 Minibatch[37601-38400]: loss = 2.203350 * 819200, metric = 0.00% * 819200;
 Minibatch[76801-78400]: loss = 0.994419 * 1638400, metric = 0.00% * 1638400;
 Minibatch[38401-39200]: loss = 2.200400 * 819200, metric = 0.00% * 819200;
 Minibatch[78401-80000]: loss = 0.988394 * 1638400, metric = 0.00% * 1638400;
 Minibatch[39201-40000]: loss = 2.208857 * 819200, metric = 0.00% * 819200;
CPU times: user 3h 28min 26s, sys: 2min 13s, total: 3h 30min 40s
Wall time: 35min 41s

In_[11]==>

# Print the generator loss 
print("Training loss of the generator is: {0:.2f}".format(G_trainer_loss))

Training loss of the generator is: 2.10

フェイク画像を生成して表示してみます :

In_[12]==>

def plot_images(images, subplot_shape):
    plt.style.use('ggplot')
    fig, axes = plt.subplots(*subplot_shape)
    for image, ax in zip(images, axes.flatten()):
        ax.imshow(image.reshape(28, 28), vmin = 0, vmax = 1.0, cmap = 'gray')
        ax.axis('off')
    plt.show()

noise = noise_sample(36)
images = G_output.eval({G_input: noise})
plot_images(images, subplot_shape =[6, 6])

少し大きめに表示してみます :

In_[13]==>

noise = noise_sample(36)
images = G_output.eval({G_input: noise})
plot_images(images, subplot_shape =[3, 3])

4. DCGAN

###4-1 概要

2 章でオリジナルの GAN 実装 (Goodfellow et al at NIPS 2014) を紹介しました。
この先駆的なワークはその後拡張されて多くのテクニックが公開されましたが、その中でも Deep Convolutional Generative Adversarial Network a.k.a. DCGAN がコミュニティにおける推奨される発射台 (= launch pad) となりました。

この章では、GAN トレーニングにおける安定性を改善するようなアーキテクチャ的な制約を持つ DCGAN の実装を紹介します。
GAN をベースにしていますので共通する項目も多いですが、相違点も多々あります :

• discriminator は strided convolution を、そして generator は fractional-strided convolution(*) を使用します。
• generator と discriminator の両者でバッチ正規化を使用します。
• generator では出力を除く総ての層のために ReLU 活性を使用します。出力層は tanh を使用します。
• discriminator では総ての層のために LeakyReLU 活性を使用します。

※ fractionally strided convolution の CNTK 実装は ConvolutionTranspose になりますが、Deconvolution という呼称の方が通りがよいかもしれません。

◆ インポートから始めます。Jupyter Notebook で新しいノートブックを作成しましょう :

In_[1]==>

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os

import cntk as C
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env() # (only needed for our build system)
C.cntk_py.set_fixed_random_seed(1) # fix a random seed for CNTK components

%matplotlib inline

基本 GAN と同様に２つの実行モード: Fast/Slow モードが用意されています :

In_[2]==>

isFast = True

4-2 データ・リーディング

データ・リーディングについては基本 GAN と同様です。以下の記事で生成された CTF フォーマットの MNIST データセットを使用します :

CNTK 2.2 Python API 入門 (3) - MNIST 総集編
2. MNIST データセットを CNTK CTF フォーマットでセーブする

本記事の目的のためには create_reader 関数が、MNIST データセットから画像を生成するために使用されるオブジェクトを返すことを知っていれば十分です。
教師なしモデルを構築していますので、features を読み込むことだけが必要で、labels は無視されます :

In_[3]==>

# Ensure the training data is generated and available for this tutorial
# We search in two locations in the toolkit for the cached MNIST data set.

data_found = False
for data_dir in [os.path.join("..", "Examples", "Image", "DataSets", "MNIST"),
                 os.path.join("data", "MNIST")]:
    train_file = os.path.join(data_dir, "Train-28x28_cntk_text.txt")
    if os.path.isfile(train_file):
        data_found = True
        break
        
if not data_found:
    raise ValueError("Please generate the data by completing CNTK 103 Part A")
    
print("Data directory is {0}".format(data_dir))

Data directory is data/MNIST

In_[4]==>

def create_reader(path, is_training, input_dim, label_dim):
    deserializer = C.io.CTFDeserializer(
        filename = path,
        streams = C.io.StreamDefs(
            labels_unused = C.io.StreamDef(field = 'labels', shape = label_dim, is_sparse = False),
            features = C.io.StreamDef(field = 'features', shape = input_dim, is_sparse = False
            )
        )
    )
    return C.io.MinibatchSource(
        deserializers = deserializer,
        randomize = is_training,
        max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1
    )

In_[5]==>

np.random.seed(123)
def noise_sample(num_samples):
    return np.random.uniform(
        low = -1.0,
        high = 1.0,
        size = [num_samples, g_input_dim]
    ).astype(np.float32)

###4-3 モデル作成

最初に、モデルのアーキテクチャ的なそして訓練用のハイパーパラメータの幾つかを設定します :

Generator

• generator ネットワークは fractional strided convolutional (ConvolutionTranspose / Deconvolution) ネットワークです。
• 入力は 100-次元ランダムベクトルです。
• 出力は 28 x 28 偽物画像の平坦化されたバージョンです。

Discriminator

• discriminator は strided-convolution ネットワークです。
• 入力として generator の 784 次元出力か本物の MNIST 画像を取り、28 x 28 画像フォーマットに reshape します。
• 出力は単一のスカラー - 入力画像が本物の MNIST 画像であると見積もられた確率です。

モデルのための計算グラフを構築します、generator と discriminator のためにそれぞれ一つずつです。

In_[6]==>

# architectural parameters
img_h, img_w = 28, 28
kernel_h, kernel_w = 5, 5 
stride_h, stride_w = 2, 2

# Generator と Discriminator の入出力パラメータ。
g_input_dim = 100
g_output_dim = d_input_dim = img_h * img_w

# 本記事ではカーネル shape は正方 (= square) であることを想定します。
# そしてストライドは各データ次元に沿って同じ長さであるとします。
if kernel_h == kernel_w:
    gkernel = dkernel = kernel_h
else:
    raise ValueError('This tutorial needs square shaped kernel') 
            
if stride_h == stride_w:
    gstride = dstride = stride_h
else:
    raise ValueError('This tutorial needs same stride in all dims')

In_[7]==>

# ヘルパー関数
def bn_with_relu(x, activation=C.relu):
    h = C.layers.BatchNormalization(map_rank=1)(x)
    return C.relu(h)

# leak=0.2 を使用するために param-relu 関数を使用します。
# 何故ならば Leakly ReLu の CNTK 実装は 0.01 に固定されているからです。
def bn_with_leaky_relu(x, leak=0.2):
    h = C.layers.BatchNormalization(map_rank=1)(x)
    r = C.param_relu(C.constant((np.ones(h.shape)*leak).astype(np.float32)), h)
    return r

Generator

最終層を除いて、fractionally strided convolution を ReLU 活性とともに使用します。
fractionally strided convolution の CNTK 実装は ConvolutionTranspose です。

最終層では generator の出力が区間 [-1, 1] に収まるように tanh 活性を使用します。
ReLU と tanh 活性化関数の使用は fractionally strided convolution の使用に加えて鍵となります :

In_[8]==>

def convolutional_generator(z):
    with C.layers.default_options(init=C.normal(scale=0.02)):
        print('Generator input shape: ', z.shape)

        s_h2, s_w2 = img_h//2, img_w//2 #Input shape (14,14)
        s_h4, s_w4 = img_h//4, img_w//4 # Input shape (7,7)
        gfc_dim = 1024
        gf_dim = 64

        h0 = C.layers.Dense(gfc_dim, activation=None)(z)
        h0 = bn_with_relu(h0)
        print('h0 shape', h0.shape)

        h1 = C.layers.Dense([gf_dim * 2, s_h4,  s_w4], activation=None)(h0)
        h1 = bn_with_relu(h1)
        print('h1 shape', h1.shape)

        h2 = C.layers.ConvolutionTranspose2D(gkernel,
                                  num_filters=gf_dim*2,
                                  strides=gstride,
                                  pad=True,
                                  output_shape=(s_h2, s_w2),
                                  activation=None)(h1)
        h2 = bn_with_relu(h2)
        print('h2 shape', h2.shape)

        h3 = C.layers.ConvolutionTranspose2D(gkernel,
                                  num_filters=1,
                                  strides=gstride,
                                  pad=True,
                                  output_shape=(img_h, img_w),
                                  activation=C.tanh)(h2)
        print('h3 shape :', h3.shape)

        return C.reshape(h3, img_h * img_w)

Discriminator

discriminator は入力 ($x^*$) として generator の 784 次元出力か本物の MNIST 画像を取り、28 x 28 画像フォーマットに reshape します。
出力は入力画像が本物の MNIST 画像であると見積もられた確率です。
ネットワークは最終層を除いて Leaky ReLU 活性を持つ strided convolution を使用してモデル化されます。
最終層では discriminator 出力が [0,1] 区間にあることを保証するために sigmoid 活性を使用します :

In_[9]==>

def convolutional_discriminator(x):
    with C.layers.default_options(init=C.normal(scale=0.02)):

        dfc_dim = 1024
        df_dim = 64

        print('Discriminator convolution input shape', x.shape)
        x = C.reshape(x, (1, img_h, img_w))

        h0 = C.layers.Convolution2D(dkernel, 1, strides=dstride)(x)
        h0 = bn_with_leaky_relu(h0, leak=0.2)
        print('h0 shape :', h0.shape)

        h1 = C.layers.Convolution2D(dkernel, df_dim, strides=dstride)(h0)
        h1 = bn_with_leaky_relu(h1, leak=0.2)
        print('h1 shape :', h1.shape)

        h2 = C.layers.Dense(dfc_dim, activation=None)(h1)
        h2 = bn_with_leaky_relu(h2, leak=0.2)
        print('h2 shape :', h2.shape)

        h3 = C.layers.Dense(1, activation=C.sigmoid)(h2)
        print('h3 shape :', h3.shape)

        return h3

トレーニングのために128 のミニバッチサイズと 0.0002 の固定された学習率を使用します :

In_[10]==>

# training config
minibatch_size = 128
num_minibatches = 5000 if isFast else 10000
lr = 0.0002
momentum = 0.5 #equivalent to beta1

###4-4 グラフを構築する

計算グラフの残りの殆どは、訓練アルゴリズムとパラメータ更新をコーディネートするためのものです。
それは GAN に関連する 2, 3 の理由のために幾分トリッキーです。
GAN は learner とパラメータの選択に過敏です。ここで選択されたパラメータの多くはコミュニティからの多くのレッスンをベースにしています :

• 第一に、discriminator は本物の MNIST 画像と generator 関数で生成された偽物の画像の両者の上で使用されなければなりません。計算グラフでこれを表わす一つの方法は、代替入力だけを別に使用して discriminator 関数の出力のクローンを作成することです。
  clone 関数で method=share を設定すれば、discriminator モデルを通した両者のパスがパラメータの同じセットを使用することを保証します。

• ２番目に、generator と discriminator モデルのために異なる損失関数からの勾配を使用して別々にパラメータを更新する必要があります。
  グラフの Function のためのパラメータを parameters 属性で得ることができます。
  けれども、モデルパラメータを更新するとき、それぞれのモデルのパラメータだけを更新します。その一方で他方のパラメータは変更されないまま保持されます。換言すれば、generator を更新するとき $G$ 関数のパラメータだけを更新します。その一方で $D$ 関数のパラメータは固定されたまま保持します。そして反対もまた同様です。

In_[11]==>

def build_graph(noise_shape, image_shape, generator, discriminator):
    input_dynamic_axes = [C.Axis.default_batch_axis()]
    Z = C.input_variable(noise_shape, dynamic_axes=input_dynamic_axes)
    X_real = C.input_variable(image_shape, dynamic_axes=input_dynamic_axes)
    X_real_scaled = X_real / 255.0

    # Create the model function for the generator and discriminator models
    X_fake = generator(Z)
    D_real = discriminator(X_real_scaled)
    D_fake = D_real.clone(
        method = 'share',
        substitutions = {X_real_scaled.output: X_fake.output}
    )

    # Create loss functions and configure optimazation algorithms
    G_loss = 1.0 - C.log(D_fake)
    D_loss = -(C.log(D_real) + C.log(1.0 - D_fake))

    G_learner = C.adam(
        parameters = X_fake.parameters,
        lr = C.learning_rate_schedule(lr, C.UnitType.sample),
        momentum = C.momentum_schedule(momentum)
    )
    D_learner = C.adam(
        parameters = D_real.parameters,
        lr = C.learning_rate_schedule(lr, C.UnitType.sample),
        momentum = C.momentum_schedule(momentum)
    )

    # Instantiate the trainers
    G_trainer = C.Trainer(X_fake,
                        (G_loss, None),
                        G_learner)
    D_trainer = C.Trainer(D_real,
                        (D_loss, None),
                        D_learner)

    return X_real, X_fake, Z, G_trainer, D_trainer

###4-5 モデルをトレーニングする

train() 関数を定義した後、トレーニングを実行します :

In_[12]==>

def train(reader_train, generator, discriminator):
    X_real, X_fake, Z, G_trainer, D_trainer = \
        build_graph(g_input_dim, d_input_dim, generator, discriminator)

    # print out loss for each model for upto 25 times
    print_frequency_mbsize = num_minibatches // 25
   
    print("First row is Generator loss, second row is Discriminator loss")
    pp_G = C.logging.ProgressPrinter(print_frequency_mbsize)
    pp_D = C.logging.ProgressPrinter(print_frequency_mbsize)

    k = 2

    input_map = {X_real: reader_train.streams.features}
    for train_step in range(num_minibatches):

        # train the discriminator model for k steps
        for gen_train_step in range(k):
            Z_data = noise_sample(minibatch_size)
            X_data = reader_train.next_minibatch(minibatch_size, input_map)
            if X_data[X_real].num_samples == Z_data.shape[0]:
                batch_inputs = {X_real: X_data[X_real].data, Z: Z_data}
                D_trainer.train_minibatch(batch_inputs)

        # train the generator model for a single step
        Z_data = noise_sample(minibatch_size)
        batch_inputs = {Z: Z_data}

        G_trainer.train_minibatch(batch_inputs)
        G_trainer.train_minibatch(batch_inputs)

        pp_G.update_with_trainer(G_trainer)
        pp_D.update_with_trainer(D_trainer)

        G_trainer_loss = G_trainer.previous_minibatch_loss_average

    return Z, X_fake, G_trainer_loss

In_[13]==>

%%time
reader_train = create_reader(train_file, True, d_input_dim, label_dim=10)

# G_input, G_output, G_trainer_loss = train(reader_train, dense_generator, dense_discriminator)
G_input, G_output, G_trainer_loss = train(reader_train,
                                          convolutional_generator,
                                          convolutional_discriminator)

Generator input shape:  (100,)
h0 shape (1024,)
h1 shape (128, 7, 7)
h2 shape (128, 14, 14)
h3 shape : (1, 28, 28)
Discriminator convolution input shape (784,)
h0 shape : (1, 12, 12)
h1 shape : (64, 4, 4)
h2 shape : (1024,)
h3 shape : (1,)
First row is Generator loss, second row is Discriminator loss
 Minibatch[   1- 200]: loss = 1.718012 * 25600;
 Minibatch[   1- 200]: loss = 1.173372 * 25600;
 Minibatch[ 201- 400]: loss = 1.712671 * 25600;
 Minibatch[ 201- 400]: loss = 1.217526 * 25600;
 Minibatch[ 401- 600]: loss = 1.712499 * 25600;
 Minibatch[ 401- 600]: loss = 1.238464 * 25600;
 Minibatch[ 601- 800]: loss = 1.708494 * 25600;
 Minibatch[ 601- 800]: loss = 1.261482 * 25600;
 Minibatch[ 801-1000]: loss = 1.706001 * 25600;
 Minibatch[ 801-1000]: loss = 1.269064 * 25600;
 Minibatch[1001-1200]: loss = 1.704771 * 25600;
 Minibatch[1001-1200]: loss = 1.274227 * 25600;
 Minibatch[1201-1400]: loss = 1.699973 * 25600;
 Minibatch[1201-1400]: loss = 1.283012 * 25600;
 Minibatch[1401-1600]: loss = 1.699864 * 25600;
 Minibatch[1401-1600]: loss = 1.283927 * 25600;
 Minibatch[1601-1800]: loss = 1.698159 * 25600;
 Minibatch[1601-1800]: loss = 1.287939 * 25600;
 Minibatch[1801-2000]: loss = 1.697151 * 25600;
 Minibatch[1801-2000]: loss = 1.289479 * 25600;
 Minibatch[2001-2200]: loss = 1.697747 * 25600;
 Minibatch[2001-2200]: loss = 1.290880 * 25600;
 Minibatch[2201-2400]: loss = 1.695999 * 25600;
 Minibatch[2201-2400]: loss = 1.294857 * 25600;
 Minibatch[2401-2600]: loss = 1.697090 * 25600;
 Minibatch[2401-2600]: loss = 1.293894 * 25600;
 Minibatch[2601-2800]: loss = 1.699475 * 25600;
 Minibatch[2601-2800]: loss = 1.289075 * 25600;
 Minibatch[2801-3000]: loss = 1.700144 * 25600;
 Minibatch[2801-3000]: loss = 1.289171 * 25600;
 Minibatch[3001-3200]: loss = 1.700021 * 25600;
 Minibatch[3001-3200]: loss = 1.288329 * 25600;
 Minibatch[3201-3400]: loss = 1.702100 * 25600;
 Minibatch[3201-3400]: loss = 1.286160 * 25600;
 Minibatch[3401-3600]: loss = 1.697719 * 25600;
 Minibatch[3401-3600]: loss = 1.286854 * 25600;
 Minibatch[3601-3800]: loss = 1.700999 * 25600;
 Minibatch[3601-3800]: loss = 1.285983 * 25600;
 Minibatch[3801-4000]: loss = 1.703385 * 25600;
 Minibatch[3801-4000]: loss = 1.281785 * 25600;
 Minibatch[4001-4200]: loss = 1.702643 * 25600;
 Minibatch[4001-4200]: loss = 1.285194 * 25600;
 Minibatch[4201-4400]: loss = 1.704002 * 25600;
 Minibatch[4201-4400]: loss = 1.276097 * 25600;
 Minibatch[4401-4600]: loss = 1.705799 * 25600;
 Minibatch[4401-4600]: loss = 1.276585 * 25600;
 Minibatch[4601-4800]: loss = 1.708148 * 25600;
 Minibatch[4601-4800]: loss = 1.275044 * 25600;
 Minibatch[4801-5000]: loss = 1.710320 * 25600;
 Minibatch[4801-5000]: loss = 1.272865 * 25600;
CPU times: user 6min 24s, sys: 1min 2s, total: 7min 26s
Wall time: 7min 46s

In_[14]==>

# Print the generator loss 
print("Training loss of the generator is: {0:.2f}".format(G_trainer_loss))

Training loss of the generator is: 1.67

####偽物の (合成) 画像を生成する

モデルのトレーニングが完了したので、generator にランダム・ノイズを供給しすることにより、偽物の画像を作成できます。
サンプルの新しいセットを取得するためには、セルを再実行すれば良いです :

In_[15]==>

def plot_images(images, subplot_shape):
    plt.style.use('ggplot')
    fig, axes = plt.subplots(*subplot_shape)
    for image, ax in zip(images, axes.flatten()):
        ax.imshow(image.reshape(28, 28), vmin=0, vmax=1.0, cmap='gray')
        ax.axis('off')
    plt.show()


noise = noise_sample(36)
images = G_output.eval({G_input: noise})
plot_images(images, subplot_shape=[6, 6])

より大きな反復数はより本物に見える MNIST 画像を生成するでしょう。そのようにして生成された画像の例は以下で示されます :

以上