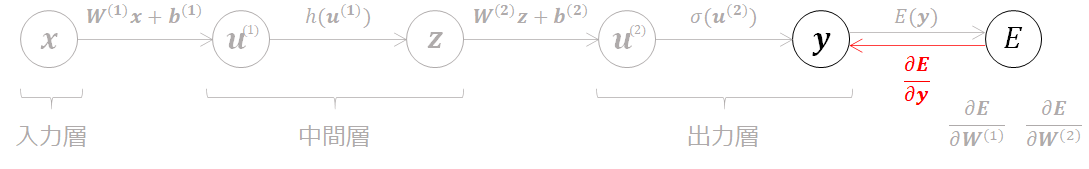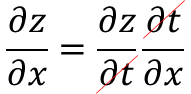本連載記事の概要
本連載記事では、全5回でDeepLearning(深層学習)をゼロから実装し、学ぶことを目的としています。
「深層学習」はなんとなく知っているけど使えない方、Pythonで動かせるけど中身がブラックボックスになっていて理解できていない方が、実際の実装を通してプログラムがどういう仕組みで動いているか理解でき、使いこなせるようになることを目指します。
連載記事目次
第1回:入力層・中間層
第2回:活性化関数
第3回:出力層
第4回:勾配降下法
第5回:誤差逆伝播法(本記事)
目次
1. 誤差勾配の計算
2. 連鎖率
3. 誤差逆伝播法
4. Pythonによる実装
5. おわりに
1. 誤差勾配の計算
ディープラーニングでは、誤差関数(E)を最小化するパラメータ(w)を求めて、精度のよい予測モデルを得ることが最終的な目的で、この誤差関数を最小化するパラメータを求めるためには勾配降下法を用いることが有効であることを第4回で学びました。
w^{(t+1)}=w^{(t)}-\eta\nabla E\\
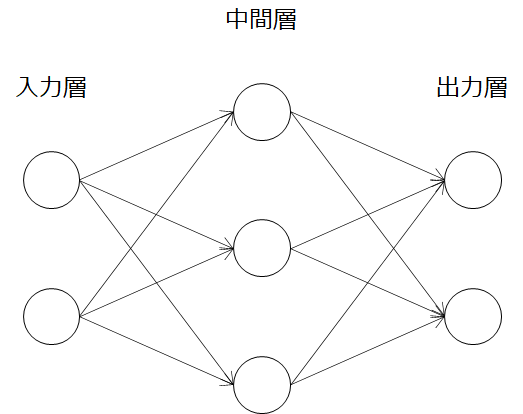
勾配降下法の式は上記の通りで、誤差関数Eの微分値(∇E)に学習率(η)をかけて重み(w)更新していけば求められることがわかります。ここで、2層のニューラルネットワークの例を考えてみましょう。(※重みを持つ層が2層なので2層ニューラルネットワークと呼んでいます。)
前述したとおり今回最適化したいパラメータは、重み(w)になるので誤差関数(E)のwの偏微分(∂E/∂w)を求めればいいわけですね。2層の重みをもつ場合は、
\nabla E=\frac{\partial E}{\partial \boldsymbol{W}}=\frac{\partial E}{\partial {W^{(1)}}}_,\frac{\partial E}{\partial {W^{(2)}}}
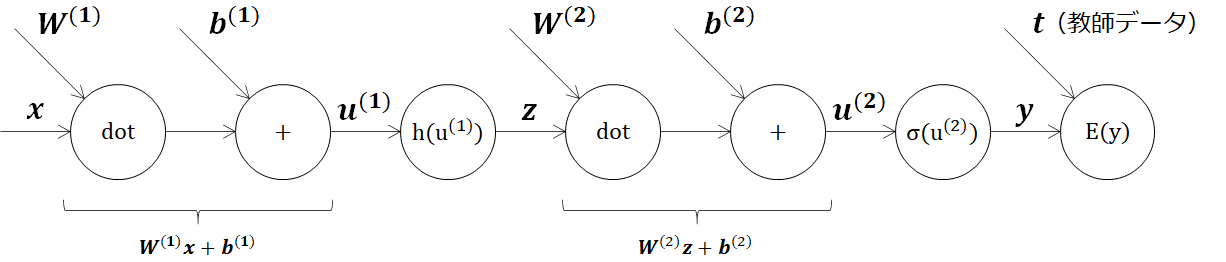
の2つの偏微分値を求めてパラメータの最適化を行えばよいわけです。そこで偏微分値を求めていきたいのですが、まずは第1回~3回で学んだように順伝播を模式的に書いてみましょう。
誤差関数Eはyの関数で、yはu(2)の関数で、・・・といった構造になっています。最終的に得られたEはyの関数なのでyで偏微分すると、
となり、これだけでは所望の勾配が求められていないことが分かります。そこで活躍するのが誤差逆伝播法です。
2. 連鎖率
誤差逆伝播法をみていく前に、誤差逆伝播法の基本原理である連鎖率を学んでいきましょう。理解をしやすくするため、次に示すような簡単な関数で説明します。
z=(x+y)^2
この関数zは、以下のような合成関数と捉えることができます。
z=t^2\\
t=(x+y)^2
計算グラフの導入
以降、誤差逆伝播法で勾配を求めるにあたり、計算グラフを導入します。
<参考になる解説記事>
・計算グラフ
計算グラフでは、ノードに演算の内容を記述し入出力を矢印で表します。
2.1. 合成関数の計算グラフ標記
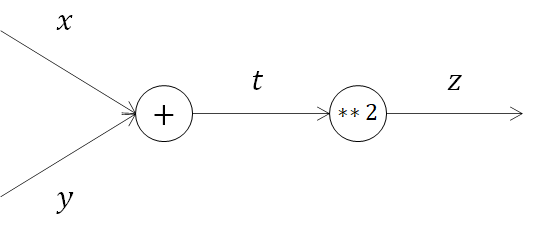
前節で導入した計算グラフを導入し、合成関数を表してみます。
できました。それではこの計算グラフを用いて連鎖率を見ていきましょう。
2.2. 合成関数の微分
連鎖率とは合成関数の微分についての性質で、次のように定義されます。
微分法において連鎖律(れんさりつ、英: chain rule)とは、複数の関数が合成された合成関数を微分するとき、その導関数がそれぞれの導関数の積で与えられるという関係式のこと。(※wikipediaより引用)
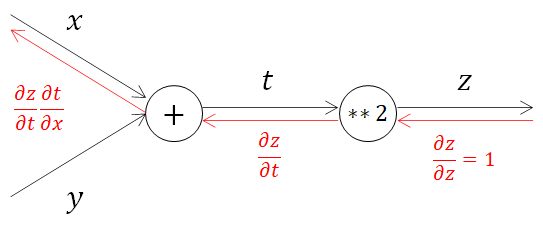
言葉だけで書かれていると分かりづらいですね。式と計算グラフで確認してみます。
\frac{\partial z}{\partial x}=\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}
合成関数の微分は、合成関数を構成するそれぞれの関数の微分の積で表すことができ、これを連鎖率の原理と呼びます。そのため、∂z/∂xは、
\frac{\partial z}{\partial t}=2t\\
\frac{\partial t}{\partial x}=1\\
\frac{\partial z}{\partial x}=2t \cdot 1 = 2(x+y)
連鎖率を使って解くことができました。この連鎖率は、下記のように∂tが互いに打ち消し合っていることも感覚的に分かりやすいですね。
2.3. ニューラルネットワークの計算グラフと連鎖率による微分
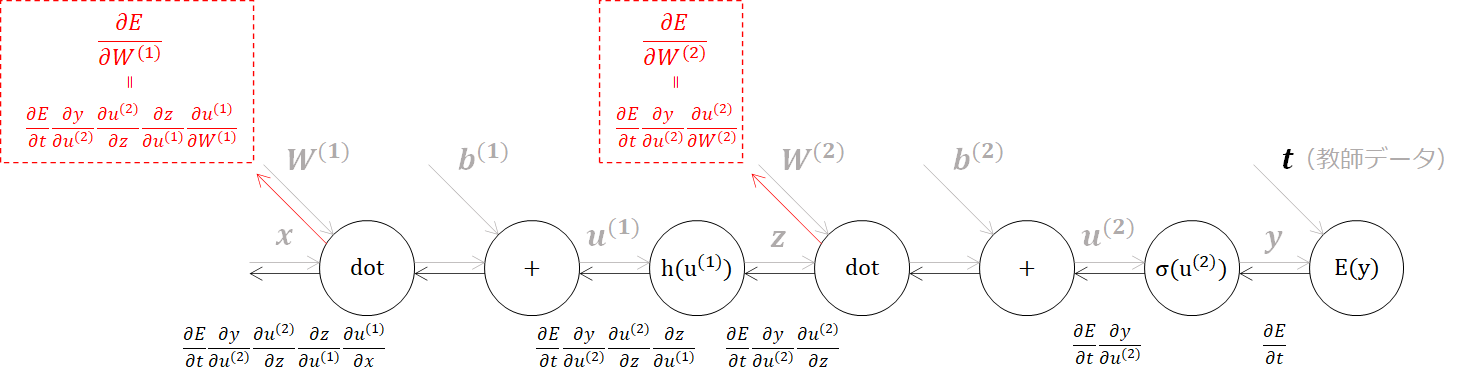
1章で示してきた2層ニューラルネットワークの合成関数を計算グラフで表していきます。活性化関数はまずはそのまま関数としておいています。
この計算グラフをもとに連鎖率を使って、合成関数の微分を解いていきます。
この連鎖率の計算グラフを解いていくと、所望の勾配(∂E/∂w)を求められていることが分かります。
\frac{\partial E}{\partial {W^{(1)}}}_,\frac{\partial E}{\partial {W^{(2)}}}
以上より、順伝播で得られた誤差関数(E)から偏微分を解き、順伝播とは逆向きに流していくことで、勾配降下法に用いる勾配が得られることが分かりました。これを誤差逆伝播法と言います。この誤差逆伝播法を用いることで、数値微分(関数に微小な変化を与えて傾きを調べる方法)をしなくてもよくなり、計算が高速に実行できるようになります。
3. 誤差逆伝播法の計算
誤差逆伝播法を用いて勾配が得られることが理解できたので、実際の計算に移っていきたいと思います。連鎖率の原理を使って合成関数の微分は、各ノードにおける微分の積で得られるので、ノード毎に確認をしていきます。
3.1. 入力層~中間層の逆伝播(Affineレイヤ)
ニューラルネットワークで行う行列の積は、幾何学の分野でアフィン変換と呼ばれます。そのためアフィン変換を行う処理をAffineレイヤという名前で実装していきます。
3.1.1. 内積の逆伝播
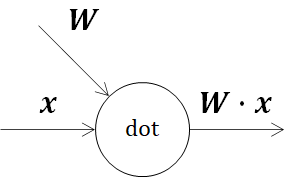
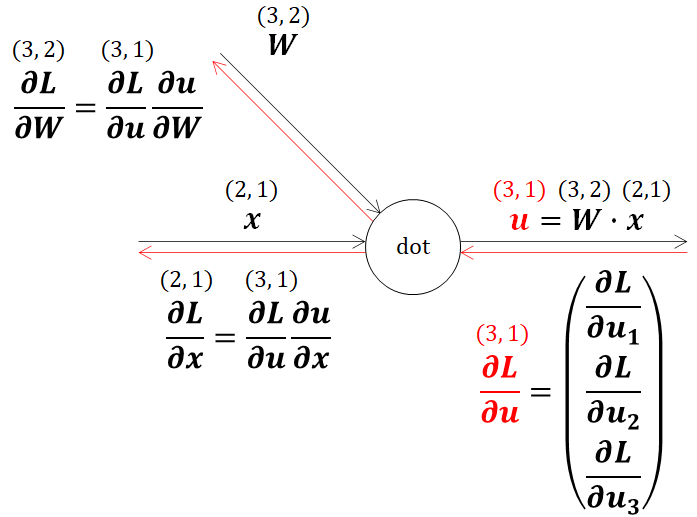
ニューラルネットワークにおいて、一番初めに出てくる内積(dot)の逆伝播を見ていきます。
理解のため、冒頭で示したニューラルネットワークと同様の形状を仮定してWを(3,2)形状、xを(2,1)形状とおくと、W・xは(3,1)形状になります。
\boldsymbol{W}=\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32}
\end{bmatrix} \quad
\boldsymbol{x} =\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix}\\
\boldsymbol{u} = \boldsymbol{W} \boldsymbol{x} =
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix} =
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}
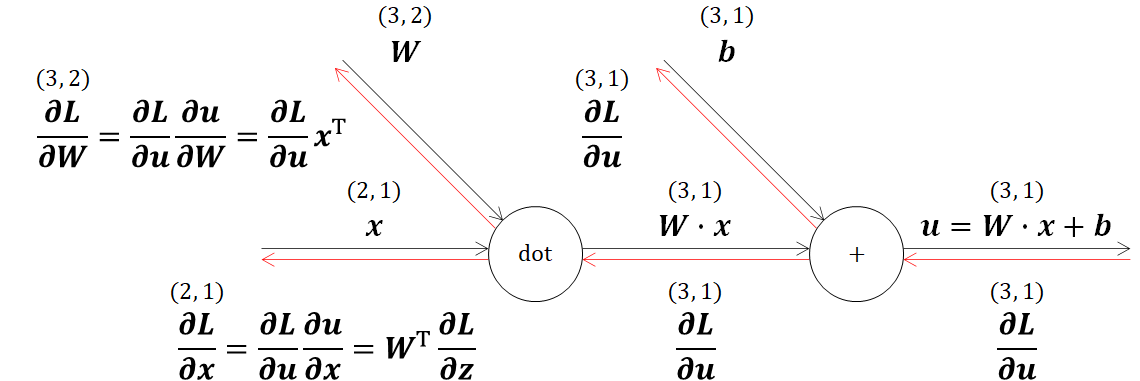
計算グラフに連鎖率の流れと、行列形状を書き加えています。ここで、出力を流れてくる偏微分値(∂L/∂u)の形状は、行列u(3,1)の偏微分値であるため、uと同様の(3,1)になります。
この計算グラフの通り最終的には∂L/∂x、∂L/∂Wを得たいのですが、連鎖率の原理が適用できるのでまずは∂u/∂x、∂u/∂Wを求めていきます。
\begin{align}
\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{x}}
&=\frac{\partial}{\partial \boldsymbol{x}}\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}\\
&=\begin{bmatrix}
\frac{\partial}{\partial x_1}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}\\
\frac{\partial}{\partial x_2}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}\\
\end{bmatrix}\\
&=\begin{bmatrix}
w_{11}&w_{21}&w_{31}\\
w_{12}&w_{22}&w_{32}
\end{bmatrix}
=\boldsymbol{W} ^\top\
\end{align}
\begin{align}
\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{W}}
&=\frac{\partial}{\partial \boldsymbol{W}}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}\\
&=\begin{bmatrix}
\frac{\partial}{\partial w_{11}}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix} &
\frac{\partial}{\partial w_{12}}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}\\
\frac{\partial}{\partial w_{21}}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix} &
\frac{\partial}{\partial w_{22}}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}\\
\frac{\partial}{\partial w_{31}}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix} &
\frac{\partial}{\partial w_{32}}
\begin{bmatrix}
w_{11}x_1 + w_{12}x_2\\
w_{21}x_1 + w_{22}x_2\\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}
\end{bmatrix}\\
&=\begin{bmatrix}
x_1 & x_2
\end{bmatrix}
=\boldsymbol{x} ^\top\
\end{align}
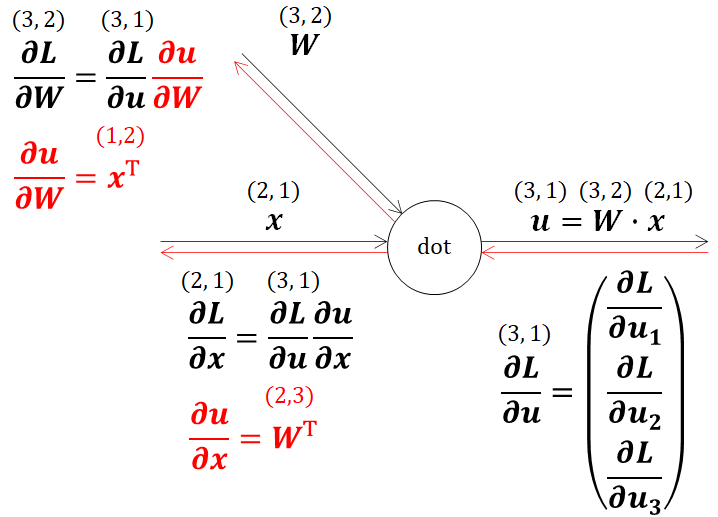
ここで、得られた∂u/∂x、∂u/∂Wの形状を考えると、∂u/∂xはWの転値になるので(2,3)、∂u/∂Wはxの転値になるので(1,2)になることがわかります。計算グラフで確認してみましょう。
得られた偏微分値を連鎖率に代入するときには、行列の掛け算の決まりごとに注意をしなければなりません。
A が n × m 行列で、B が m × p 行列ならば、それらの行列の積 AB が n × p 行列として与えられ、その成分は A の各行の m 個の成分がそれぞれ順番に B の各列の m 個の成分と掛け合わされる形で与えられる
Wikipediaより引用
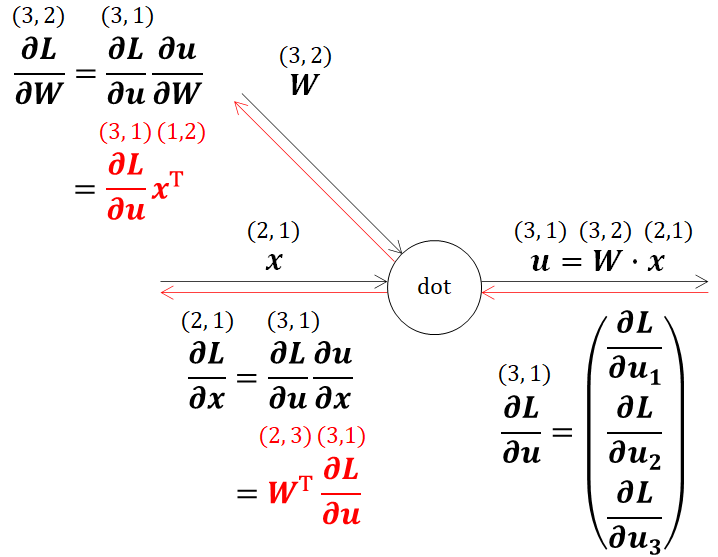
この引用文から、前からかける行列の列(A)と後ろの行列(B)の行が一致していないといけませんでした。この基本原理に基づいて、連鎖率に解いた偏微分値を代入すると、
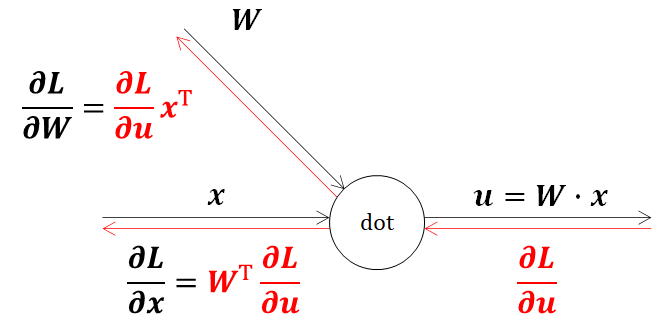
となります。式が色々あって分かりづらいので、最終的な結果だけを以下に示します。
以上で内積の偏微分値が得られました。
3.1.2. 加算の逆伝播
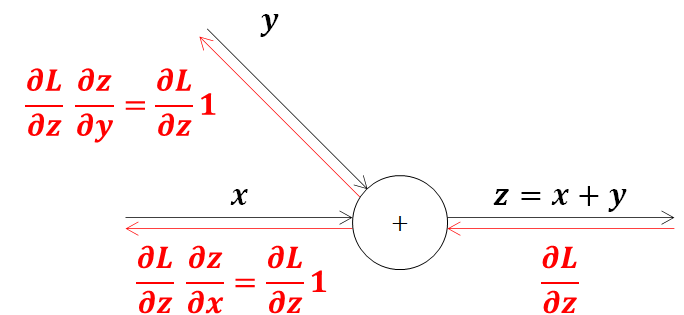
加算の式を単純化して計算グラフで連鎖率を表してみます。z=x+yのような簡単な関数を考えると分かりますが、加算ノードは流れてきた微分値をそのまま流すだけになります。
\frac{\partial z}{\partial x}=\frac{\partial (x+y)}{\partial x}=1\\
\frac{\partial z}{\partial y}=\frac{\partial (x+y)}{\partial y}=1
ここでニューラルネットの入力層~中間層に置き換えて考えてみます。活性化関数に入れる前の出力(u)は、入力(x)と重み(w)の内積に、バイアス(b)を加えた以下の構造になっています。それでは計算グラフにしてみましょう。
以上で、入力層~中間層の逆伝播を理解することができました。
3.2. 中間層の活性化関数の逆伝播
3.2.1. Sigmoid関数の逆伝播(Sigmoidレイヤ)
引き続いてSigmoid関数の逆伝播を考えていきます。Sigmoid関数は以下の式で表されます。
h(x)=\frac{1}{1+\exp(-a)} \
これを計算グラフで表してみましょう。
少し長いですが、表すことができました。逆伝播を順に確認していきます。最初の除算ノードですが、単純化したものを確認すると理解しやすいです。
y=\frac{1}{x}\\
\begin{align}
\frac{\partial y}{\partial x}&=\frac{\partial}{\partial x} (\frac{1}{x})\\
&=-\frac{1}{x^2}\\
&=-y^2\\
\end{align}
これより、Sigmoid関数の計算グラフとしては
除算ノードの次は加算ノードですが、加算ノードはそのまま流すだけでした。
次は指数関数(exp)ノードですが、その微分は次の式で表されます。
y=\exp(x)\\
\frac{\partial y}{\partial x}=exp(x)
そのまま入力の指数関数を返します。そのためSigmoid関数の計算グラフは以下の通りです。
最後に乗算ノードです。乗算の微分を式で表すと、
z=x×y\\
\begin{align}
\frac{\partial z}{\partial x}&=\frac{\partial}{\partial x} (x×y)\\
&=y\\
\frac{\partial z}{\partial y}&=\frac{\partial}{\partial y} (x×y)\\
&=x\\
\end{align}
となります。この乗算の逆伝播は、ちょうど入力信号をひっくり返したようになります。そのため計算グラフは次の通りになります。
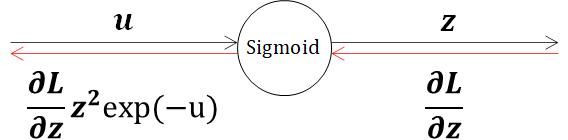
以上でSigmoid関数の逆伝播が完了しました。出力の結果だけ確認すると、
となります。ここで、逆伝播で得られた式を変形していくと、
\begin{align}
\frac{\partial L}{\partial u} z^2 exp(-u)
&=\frac{\partial L}{\partial u} \frac{1}{(1+exp(-u))^2} exp(-u) \\
&=\frac{\partial L}{\partial u} \frac{1}{1+exp(-u)} \frac{exp(-u)}{1+exp(-u)} \\
&=\frac{\partial L}{\partial u} z(1-z)
\end{align}
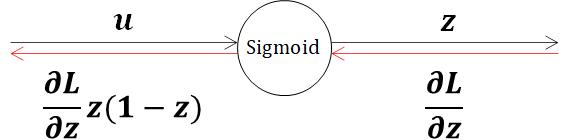
となり、Sigmoid関数の微分はSigmoid関数だけで表現できることがわかります。以上より、最終的には以下の形になります。
3.2.2. ReLU関数の逆伝播(ReLUレイヤ)
活性化関数として使われるReLU(Rectified Linear Unit)は、次の式で表されました。
y=\left\{
\begin{array}
xx & (x > 0) \\
0 & (x \leqq 0)
\end{array}
\right.
この式の微分は、
\frac{\partial y}{\partial x}=\left\{
\begin{array}
x1 & (x > 0) \\
0 & (x \leqq 0)
\end{array}
\right.
3.3. 出力層の逆伝播(Softmax-with-Lossレイヤ)
最後に出力層であるソフトマックス関数と誤差関数をセットでついて説明していきます。
3.3.1. Softmax関数と交差エントロピー誤差の順伝播
Softmax関数は、次の式で表されます。(詳しくは、第3回記事を参照してください。)
y_k(u)=\frac{exp(u_k)}{\sum_{i=1}^{n}exp(u_i)} \
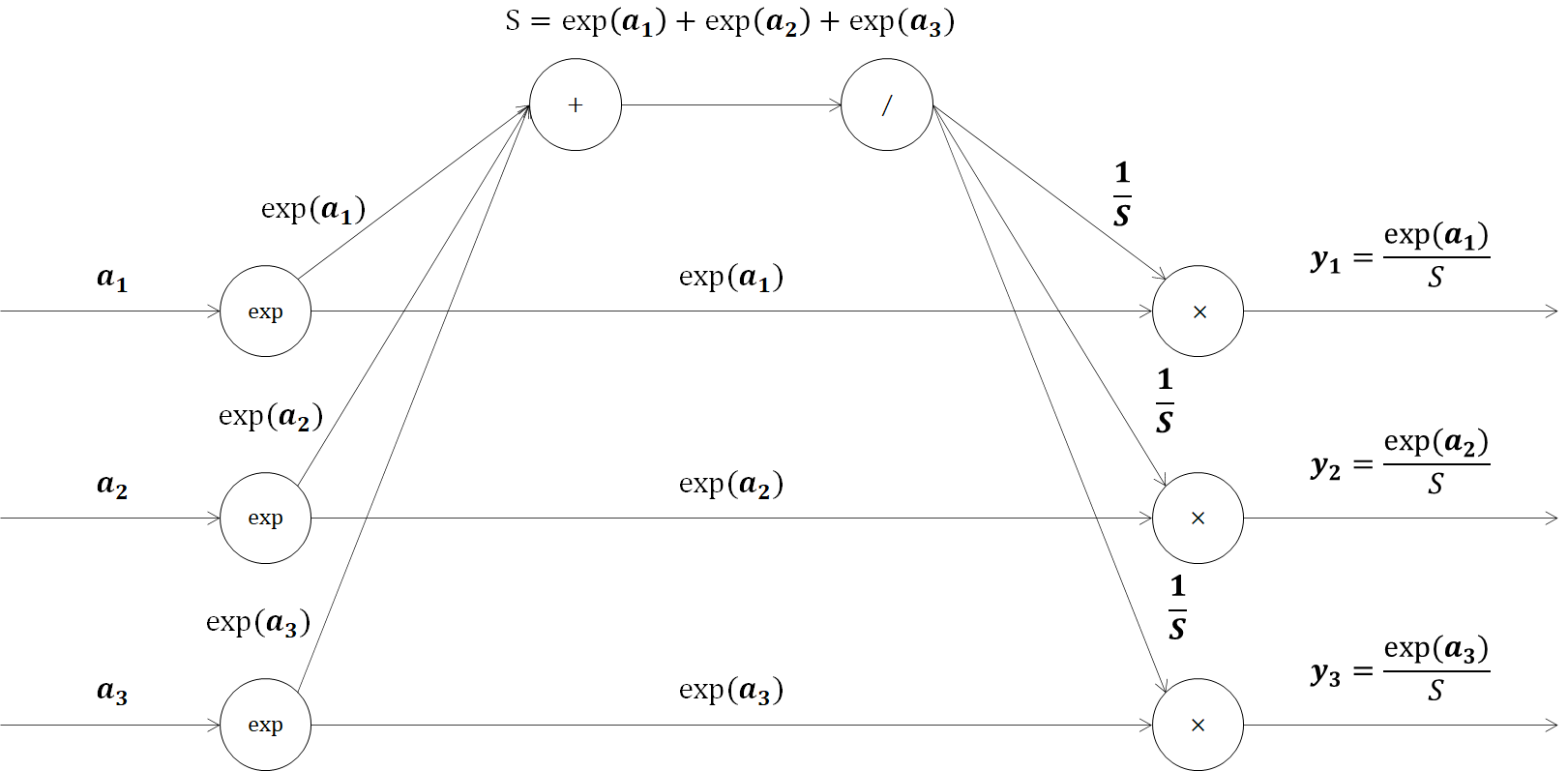
このSoftmax関数の順伝播の計算グラフを表します。
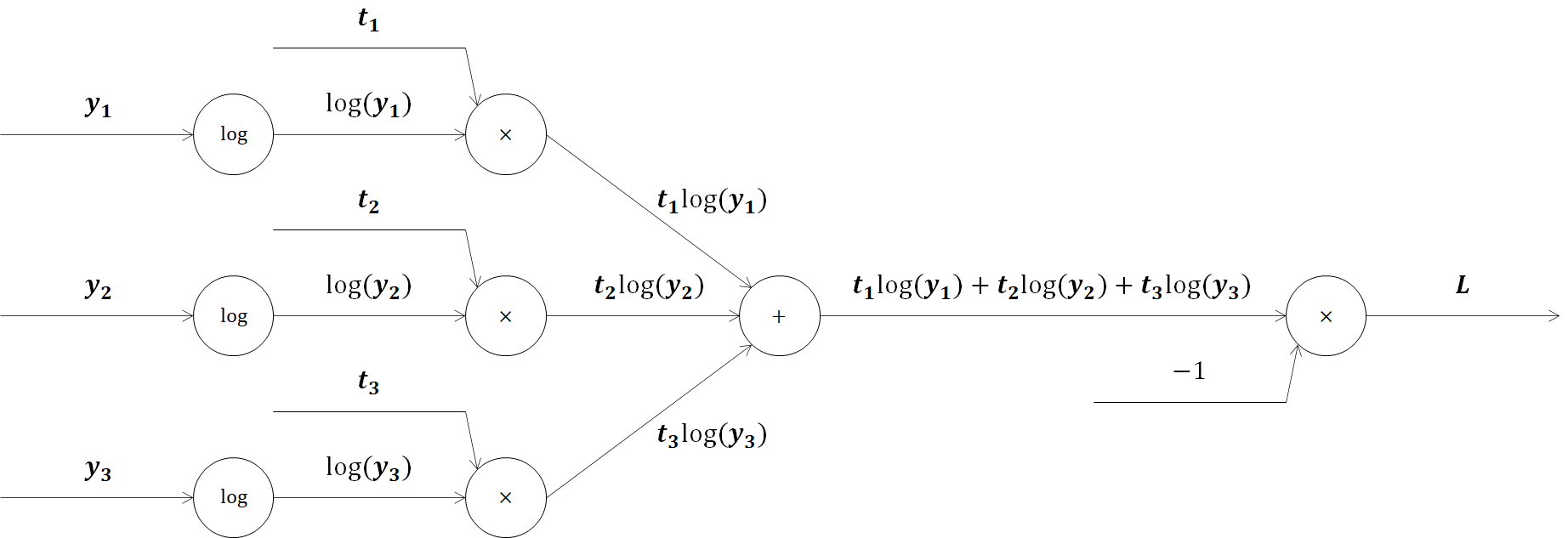
続いて、交差エントロピー誤差を式で表すと、
y_k(u)=-\sum_{k} t_k\log y_k
であるため、計算グラフは
と表されます。これらをセットにして、逆伝播を見ていきましょう。
3.3.2. Softmax関数と交差エントロピー誤差の逆伝播
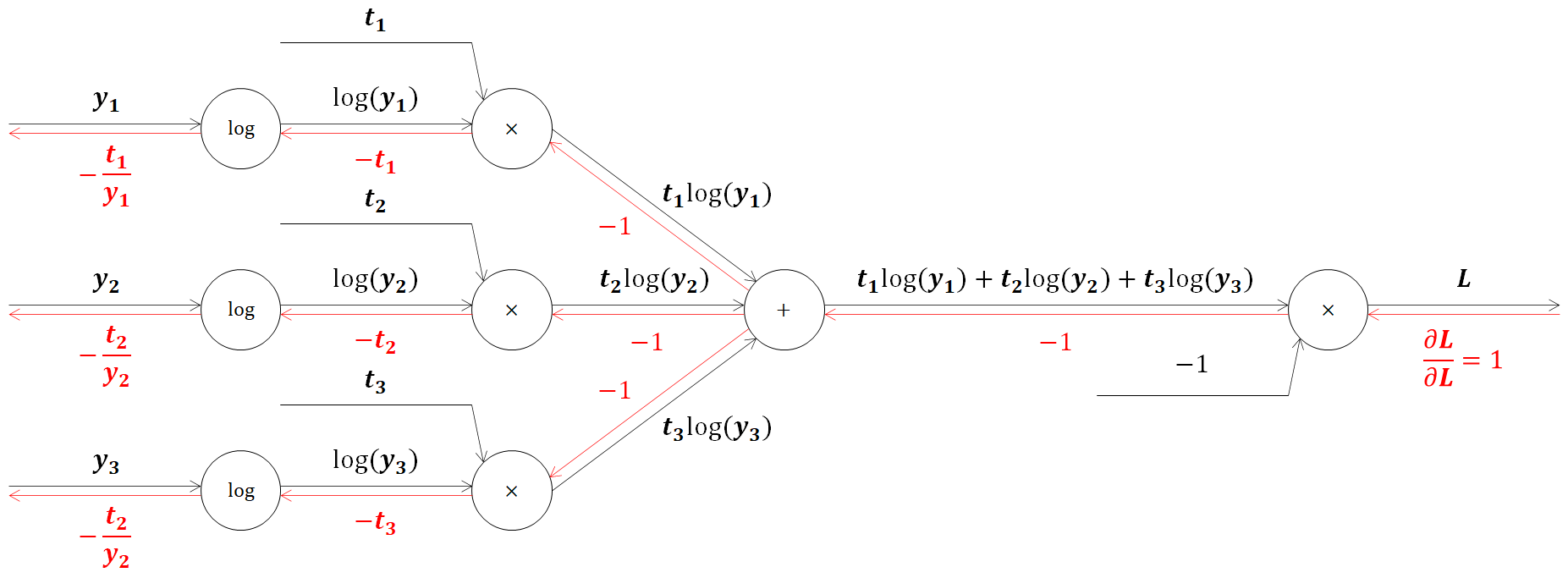
まずは交差エントロピー誤差の逆伝播からです。これまで学んできた乗算、加算ノードを使い、logの微分を下記の通りにすれば簡単に計算グラフを作成することができます。
y = \log x\\
\frac{\partial y}{\partial x}=\frac{1}{x}
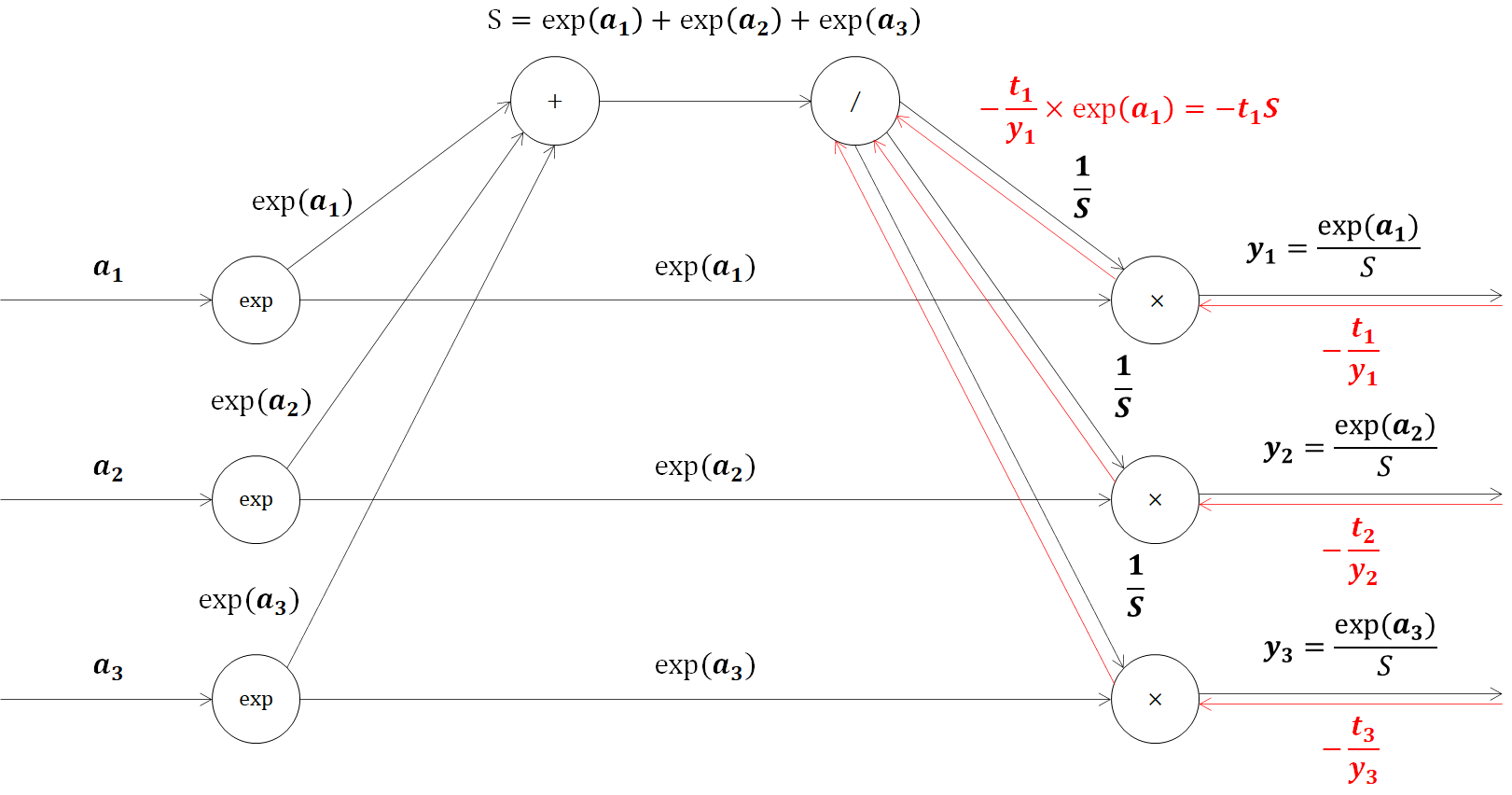
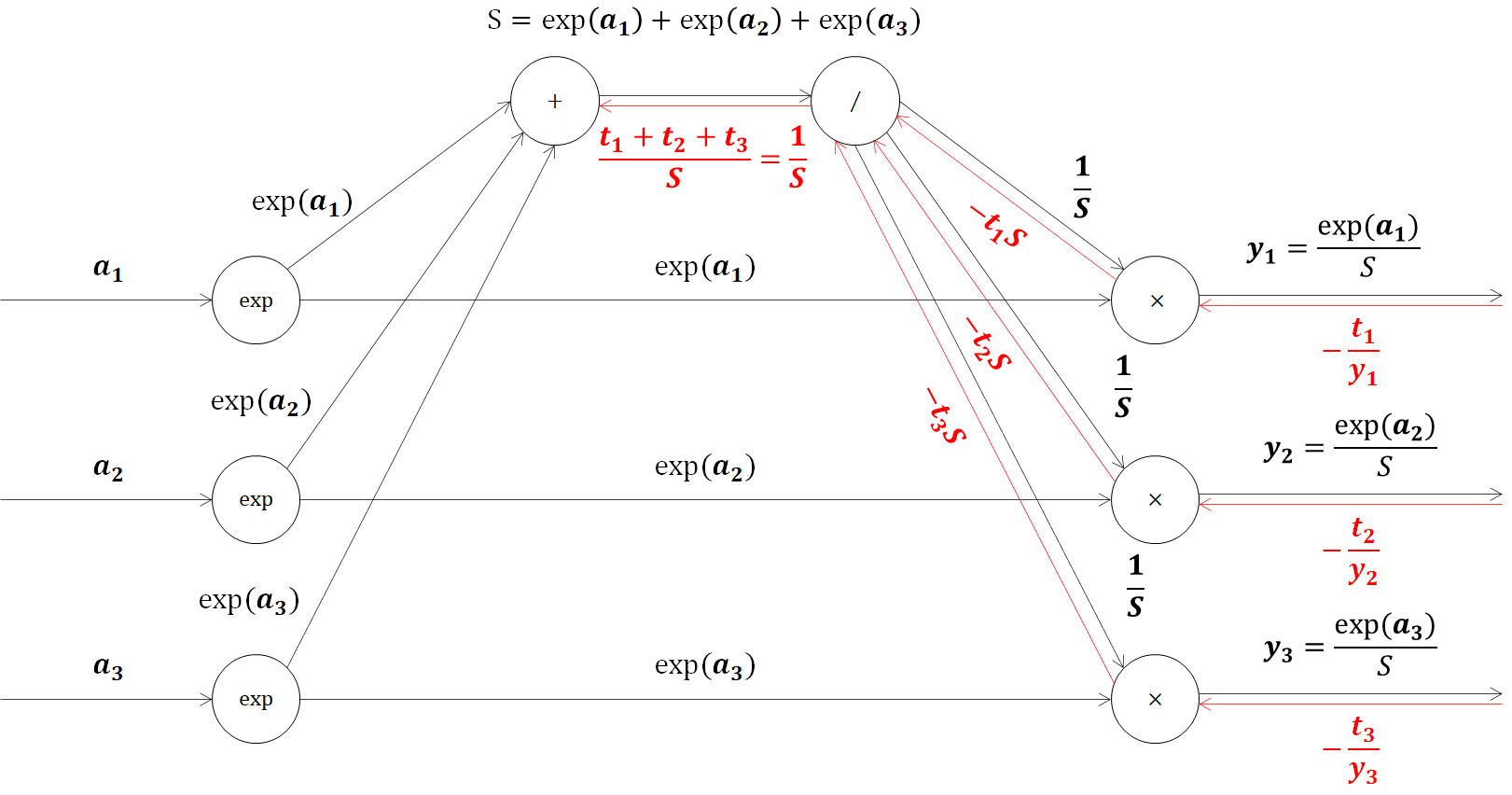
続いてSoftmax関数の逆伝播を見ていきます。最初は交差エントロピー誤差から流れてきた値に、乗算ノードで順伝播の値をひっくり返して乗算します。(※一部記述を省略しています)
ここで、この乗算ノードで得られた値をよくみると、
\begin{align}
-\frac{t_1}{y_1} × \exp(a_1) &= -t_1 × \frac{S}{\exp (a_1)} × \exp(a_1)\\
&=-t_1S
\end{align}
となり、単純化されることがわかりますね。次のステップを確認してみます。除算ノードに-t1S、-t2S、-t3Sまで3つの値が流れるので、この和の微分値を逆伝播します。
ここで、乗算ノードのため、
y = \frac{1}{x}=x^{-1}\\
\begin{align}
\frac{\partial y}{\partial x}&=-x^{-2}\\
&=-\frac{1}{x^2}\\
\end{align}
-(t_1+t_2+t_3)S×(-\frac{1}{S^2}) = \frac{t_1+t_2+t_3}{S}
となります。ここで、t1、t2、t3は教師データで、すべてを足すと1になりそれぞれが確率を意味する値でした。そのため、t1、t2、t3の合計は1になるため、逆伝播の値は以下のように簡単な形で表すことができます。
\frac{t_1+t_2+t_3}{S} = \frac{1}{S}
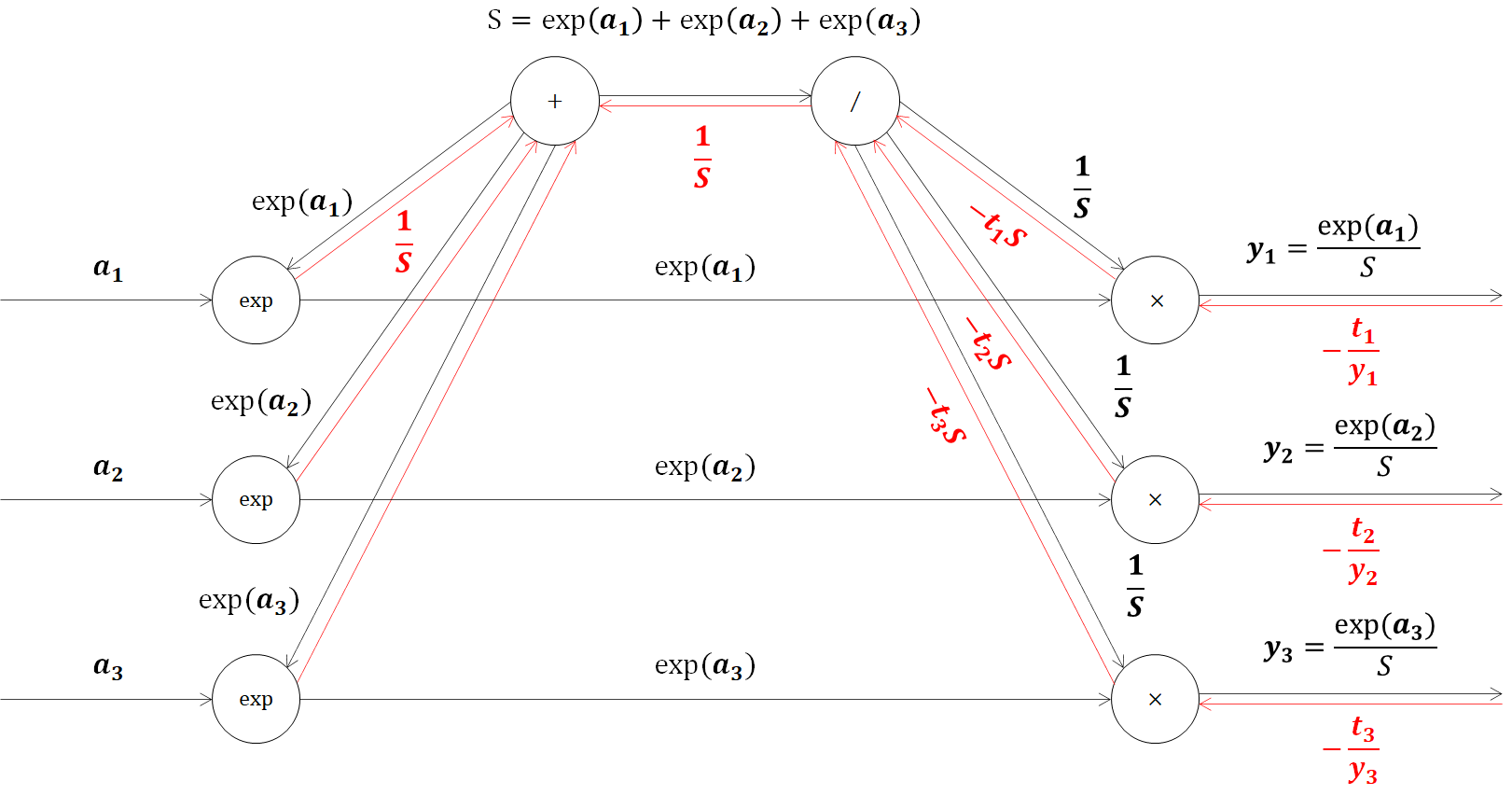
次の加算ノードは、値をそのまま流すだけでした。
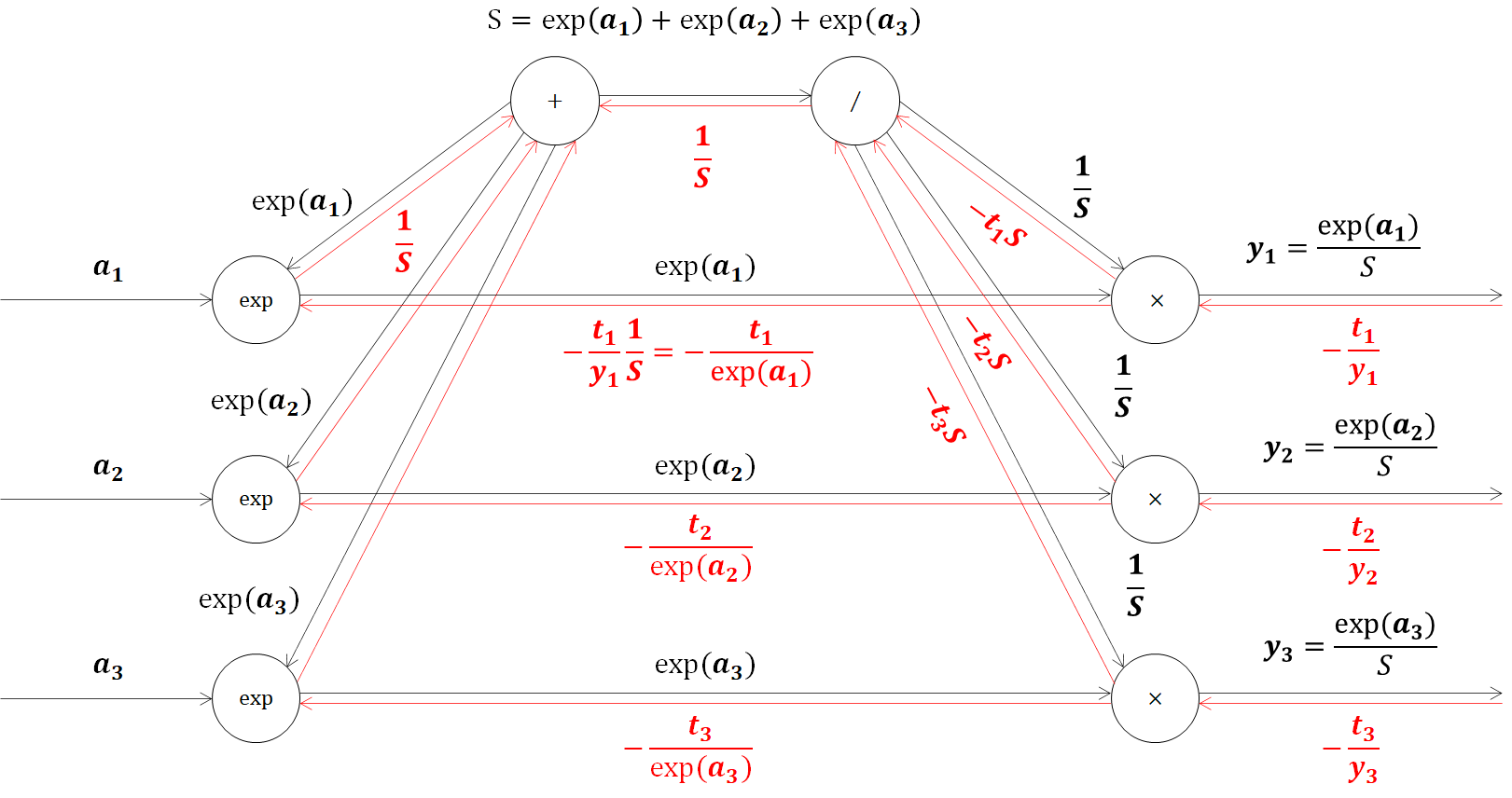
それでは、個別の逆伝播の計算グラフに移ります。乗算ノードなので、ひっくりかえして値を流すと、ここも式を簡単にすることができます。
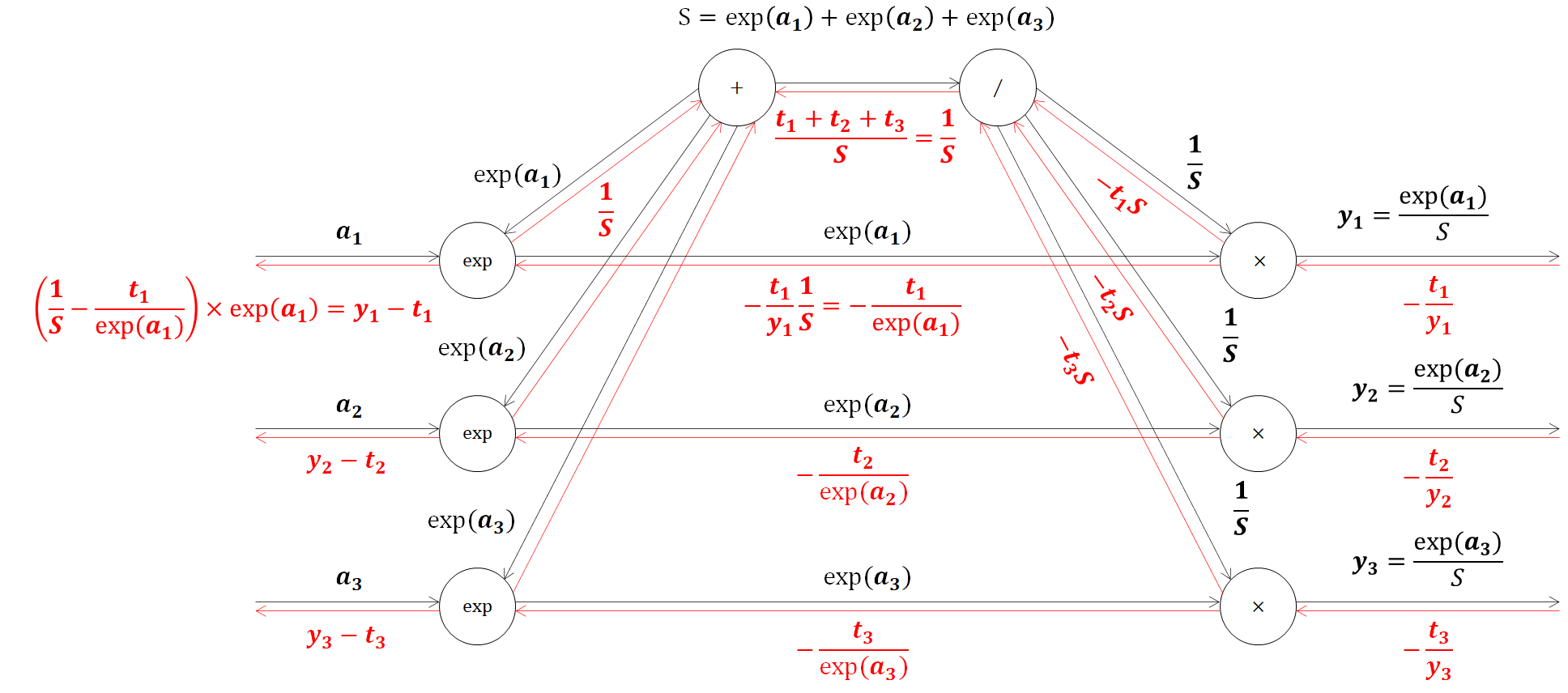
最後に、expノードです。expノードに2つの逆伝播が流れてくるのでこれを足した値に、expノードの微分値をかけて求めることができます。
\begin{align}
(\frac{1}{S}-\frac{t_1}{exp(a_1)}) × exp(a_1) &= \frac{1}{S}\\
&=\frac{exp(a_1)}{S}-t_1\\
&=y_1-t_1
\end{align}
以上で、Softmax関数と交差エントロピー誤差の逆伝播を解くことができました。
4. Pythonでの実装
それでは、ここまで学んできた逆伝播をPythonで実装していきます。2層ニューラルネットワーク(入力層2ノード、中間層3ノード、出力層2ノード)で、中間層の活性化関数はReLU、出力層の活性化関数はソフトマックス関数、誤差関数は交差エントロピー誤差を利用します。
import numpy as np
# 行列をわかりやすく表示するための関数
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
#print("shape: " + str(x.shape))
print("")
# 今回使用する活性化関数、誤差関数の関数を作成(別ファイルで作成して起き、importしてもOK)
# ReLU関数
def relu(x):
return np.maximum(0, x)
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
# クロスエントロピー
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
# 逆伝播用
# ReLU関数の導関数
def d_relu(x):
return np.where( x > 0, 1, 0)
# シグモイドとクロスエントロピーの複合導関数
def d_softmax_with_loss(t, y):
return y - t
# ニューラルネットワークを作成する関数を定義
# ウェイトとバイアスを設定
def init_network():
print("##### ネットワークの初期化 #####")
network = {}
network['W1'] = np.array([
[0.1, 0.3, 0.5],
[0.2, 0.4, 0.6]
])
network['W2'] = np.array([
[0.1, 0.4],
[0.2, 0.5],
[0.3, 0.6]
])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['b2'] = np.array([0.1, 0.2])
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])
return network
# 順伝播
def forward(network, x):
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = relu(u1)
u2 = np.dot(z1, W2) + b2
y = softmax(u2)
# 誤差の算出
loss = cross_entropy_error(t, y)
print_vec("総入力1", u1)
print_vec("中間層出力1", z1)
print_vec("総入力2", u2)
print_vec("出力1", y)
print("出力合計: " + str(np.sum(y)))
print("誤差: " + str(loss))
return y, z1
# 誤差逆伝播
def backward(x, d, z1, y):
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = d_softmax_with_loss(t, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * d_relu(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
少し長いですが、使用する各関数の定義、ニューラルネットワークの初期化、順伝播、逆伝播の関数を作成しました。
それでは実際に動かしていきます。まずは、入力と教師データを準備し、順伝播を流して学習前の誤差をみましょう。
# 訓練データ
x = np.array([[5.0, 1.0]])
# 目標出力
t = np.array([[0, 1]])
# 学習率
learning_rate = 0.01
network = init_network()
y, z1 = forward(network, x)
> ##### ネットワークの初期化 #####
*** 重み1 ***
[[0.1 0.3 0.5]
[0.2 0.4 0.6]]
*** 重み2 ***
[[0.1 0.4]
[0.2 0.5]
[0.3 0.6]]
*** バイアス1 ***
[0.1 0.2 0.3]
*** バイアス2 ***
[0.1 0.2]
*** 総入力1 ***
[[0.8 2.1 3.4]]
*** 中間層出力1 ***
[[0.8 2.1 3.4]]
*** 総入力2 ***
[[1.62 3.61]]
*** 出力1 ***
[[0.12025686 0.87974314]]
出力合計: 1.0
誤差: 0.12812518961618194
求めることができました。出力を見ると分類ラベルはクラス1の確率が88%でクラス1を出力しているため結果は合っていますが、クラス0の確率が10%くらい残されていますね。これを誤差逆伝播を用いて学習させていきます。
iters_num = 100 # 学習を100回更新する
for i in range(iters_num):
grad = backward(x, t, z1, y)
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]
print("##### 結果表示 #####")
print("##### 更新後パラメータ #####")
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])
> ##### 結果表示 #####
##### 更新後パラメータ #####
*** 重み1 ***
[[0.33765368 0.6307148 0.92377592]
[0.24753074 0.46614296 0.68475518]]
*** 重み2 ***
[[ 0.00379451 0.49620549]
[-0.05253941 0.75253941]
[-0.10887333 1.00887333]]
*** バイアス1 ***
[0.14753074 0.26614296 0.38475518]
*** バイアス2 ***
[-0.02025686 0.32025686]
# 学習モデルでの再計算
# 訓練データ
x = np.array([[1.0, 5.0]])
# 目標出力
t = np.array([[0, 1]])
# 順伝播と誤差の計算
y, z1 = forward(network, x)
> *** 総入力1 ***
[[1.72283809 3.22757256 4.73230703]]
*** 中間層出力1 ***
[[1.72283809 3.22757256 4.73230703]]
*** 総入力2 ***
[[-0.69851633 8.3783125 ]]
*** 出力1 ***
[[1.14270386e-04 9.99885730e-01]]
出力合計: 1.0
誤差: 0.00011417690406179714
誤差がかなり小さくなりました。出力もクラス1の確率がほぼ100%ですね。以上で、順伝播から誤差逆伝播までの実装が完了しました。
5. おわりに
本連載では、ニューラルネットワークの入力層から出力層で行われている計算と、誤差を小さくする誤差逆伝播法に触れながら、Pythonでの実装を行い実践的に身に着けて学びました。Pythonライブラリを使えばだれでも使えますが、中身を理解しながら使用するのと、理解せず使用するのでは、見方が大きく変わると思います。
今後も引き続き、ディープラーニング、機械学習に関する記事を書いていくので、参考にしてください。
連載記事目次
第1回:入力層・中間層
第2回:活性化関数
第3回:出力層
第4回:勾配降下法
第5回:誤差逆伝播法(本記事)
参考文献
この記事は以下の情報を参考にして執筆しました。
参考:ゼロから作るDeepLearning, O'REILLY社