本連載記事の概要
本連載記事では、全5回でDeepLearning(深層学習)をゼロから実装し、学ぶことを目的としています。
「深層学習」はなんとなく知っているけど使えない方、Pythonで動かせるけど中身がブラックボックスになっていて理解できていない方が、実際の実装を通してプログラムがどういう仕組みで動いているか理解でき、使いこなせるようになることを目指します。
連載記事目次
第1回:入力層・中間層
第2回:活性化関数(本記事)
第3回:出力層
第4回:勾配降下法
第5回:誤差逆伝播法
目次
1. 活性化関数の概要
2. 中間層の活性化関数
3. ニューラルネットワークの数式化
4. Pythonによる実装
5. おわりに
1. 活性化関数の概要
活性化関数とは、ニューラルネットワークにおける入力から、次の層への出力を決定するための非線形な関数です。入力値の値により、次の層への信号の大きさや、信号を流す/流さないを決める機能を持っています。
本連載の第1回目では入力層・中間層の実装を学びましたが、その中間層出力(u)を次の層に送るときに活用する関数が活性化関数(h)になります。
2. 中間層の活性化関数
それでは活性化関数の具体例を実装しながら学んでいきましょう。本記事では、主に中間層用の活性化関数を確認していきます。
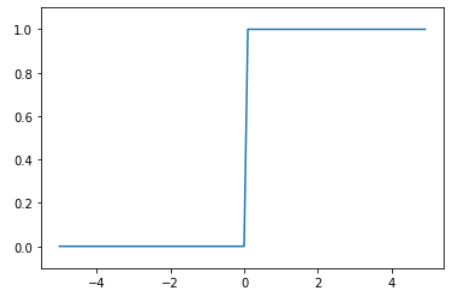
2.1. ステップ関数
ステップ関数は信号を流す(1)/流さない(0)の二値の出力で、パーセプトロンで用いられていた関数です。0、1しか表現できず、線形分離可能なものにしか学習ができません。pythonでの実装し、グラフを示します。
import numpy as np
import matplotlib.pyplot as plt
# ステップ関数
def step_function(x):
y = x > 0
return y.astype(np.int)
# グラフ化
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
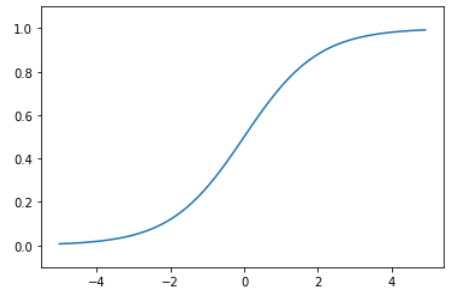
2.2. シグモイド関数
シグモイド関数は0~1の間の数値を取る関数で、信号の強弱を伝えることができます。ニューラルネットワークでの分類をする場合に、各ラベルの予測を確率で示すことができます。
一方で、ディープニューラルネットワークでは勾配が消失してしまう、といった課題があります。
# シグモイド関数
def sigmoid(x):
return 1/(1 + np.exp(-x))
# グラフ化
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
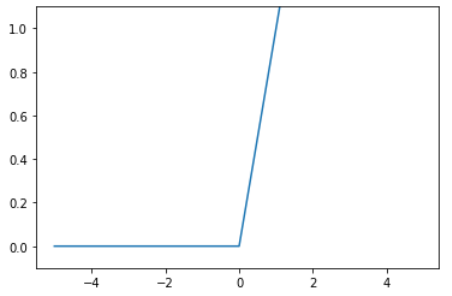
2.3. ReLU関数(Rectified Linear Unit)
シグモイド関数は古くからニューラルネットワークに利用されてきましたが、今最も使われている活性化関数はこのRuLU関数です。0以上は値をそのまま返すので勾配消失の回避と、0以下を0で返すのでスパース化(sparse:疎)に貢献でき、精度が向上しやすい活性化関数です。
# ReLU関数
def relu(x):
return np.maximum(0, x)
# グラフ化
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
3. ニューラルネットワークの数式化
ここまでに活性化関数をいくつか紹介してきました。前回学んだ入力層・出力層と活性化関数を組み合わせて、ニューラルネットワークの順伝播(forward_propagation)を実装していきましょう。
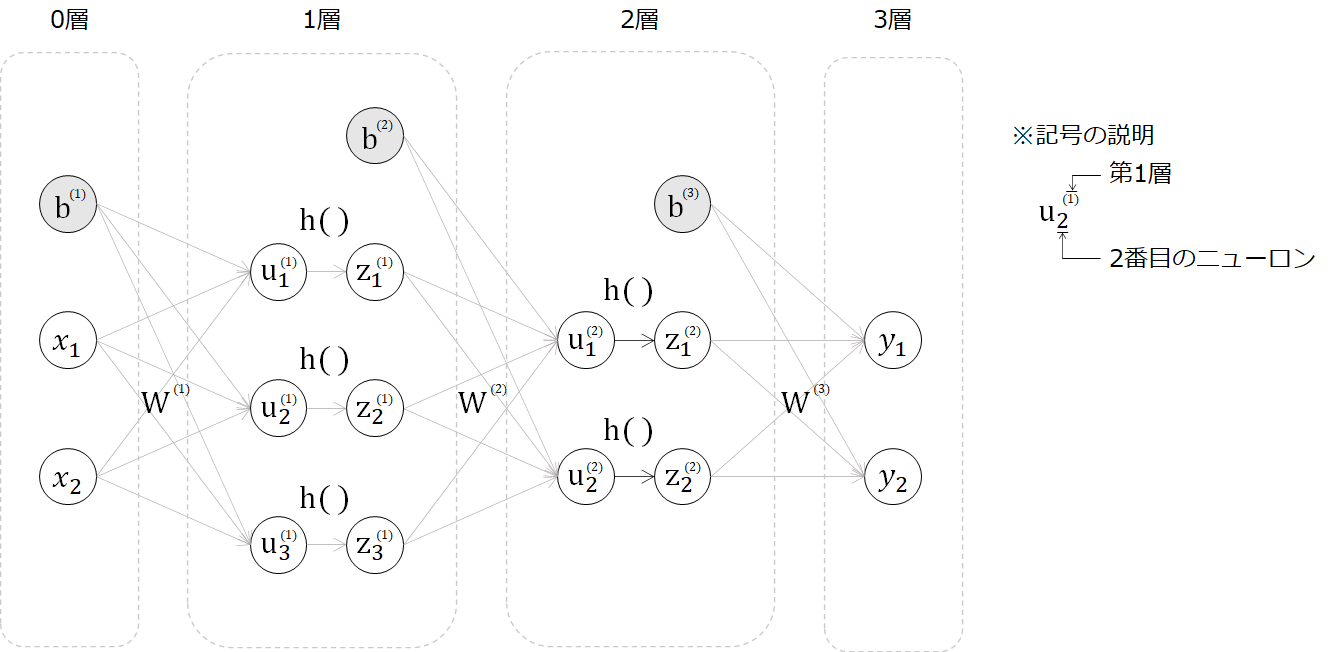
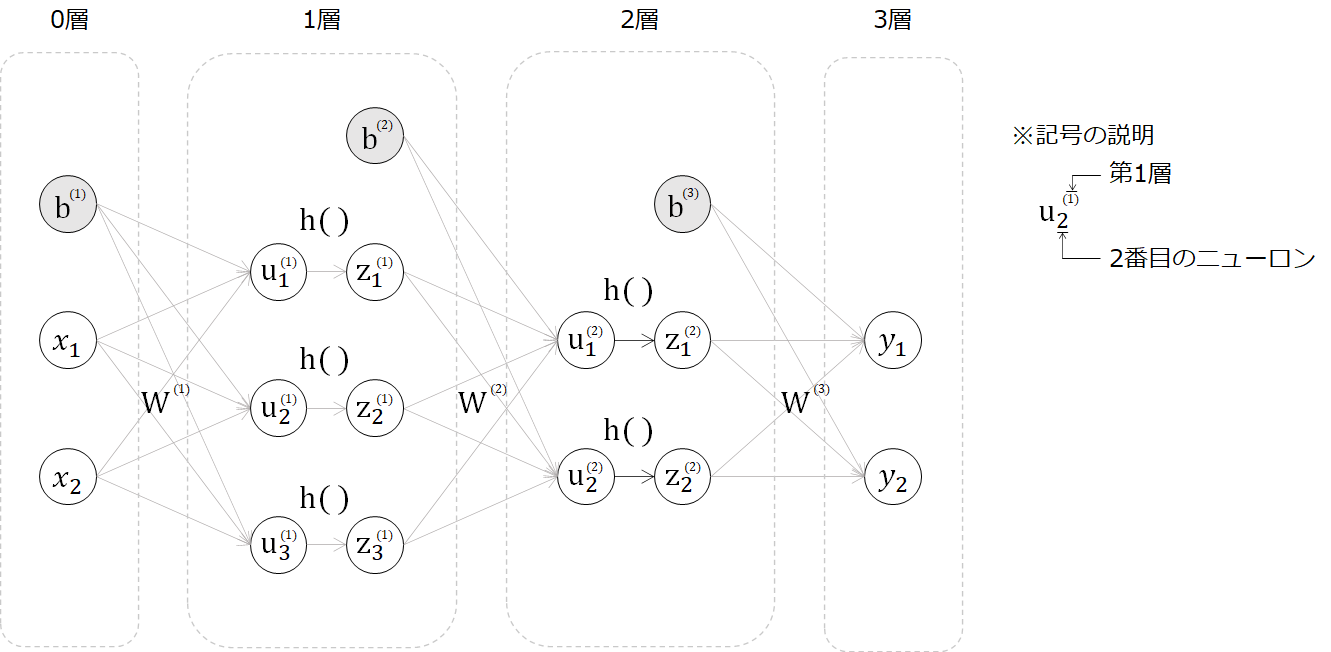
第1回目は、下記図の0~1層の活性化関数(h)前までを実装しましたが、今回は活性化関数で各層をつなげ、3層のニューラルネットワークを作成します。
まずは数式を追っていきます。第1層の入力から中間層は次の通りです(※詳細は第1回目参照)。
\begin{bmatrix}
u^{(1)}_1 \\
u^{(1)}_2 \\
u^{(1)}_3
\end{bmatrix} =
\begin{bmatrix}
w^{(1)}_{11} & w^{(1)}_{12} \\
w^{(1)}_{21} & w^{(1)}_{22} \\
w^{(1)}_{31} & w^{(1)}_{32}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix} +
\begin{bmatrix}
b^{(1)}_1 \\
b^{(1)}_2 \\
b^{(1)}_3
\end{bmatrix}
\boldsymbol{u^{(1)}} = \boldsymbol{W^{(1)}} \boldsymbol{x} + \boldsymbol{b^{(1)}}
この中間層(u)を活性化関数(h, シグモイド関数)に入れます。(※以降は行列表現でのみ記述していきます。)
\boldsymbol{z^{(1)}} = h(\boldsymbol{u^{(1)}})\\
h(x)=\frac{1}{1+\exp(-a)} \
この得られたzに重みとバイアスを加えて2層目の中間層を得て、再び活性化関数に入れます。
\boldsymbol{u^{(2)}} = \boldsymbol{W^{(2)}} \boldsymbol{z^{(1)}} + \boldsymbol{b^{(2)}}\\
\boldsymbol{z^{(2)}} = h(\boldsymbol{u^{(2)}})
最後に今までと同じ処理をして出力を得ます。出力層のyは、出力をそのまま流す恒等写像を想定しています。
\boldsymbol{u^{(3)}} = \boldsymbol{W^{(3)}} \boldsymbol{z^{(2)}} + \boldsymbol{b^{(3)}}\\
\boldsymbol{y} = h(\boldsymbol{u^{(3)}})
4. Pythonによる実装
前章まで扱ってきたニューラルネットワークの順伝播(forward_propagation)を実装していきましょう。
import numpy as np
# シグモイド関数(ロジスティック関数)
def sigmoid(x):
return 1/(1 + np.exp(-x))
# 行列、行列形状の出力用
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
print("shape: " + str(vec.shape))
print("")
# ニューラルネットワークのサイズ設定 入力層:1層(2ノード), 中間層:2層(3ノード・2ノード), 出力層:1層(2ノード)
def init_network():
# ネットワークの初期化
network = {}
input_layer_size = 2
hidden_layer_size_1 = 3
hidden_layer_size_2 = 2
output_layer_size = 2
# ネットワークの初期値設定
network['W1'] = np.array([[0.1,0.2],[0.3,0.4],[0.5,0.6]])
network['W2'] = np.array([[0.1, 0.2, 0.3],[0.4, 0.5, 0.6]])
network['W3'] = np.array([[0.1,0.2],[0.3,0.4]])
network['b1'] = np.array([0.1,0.2,0.3])
network['b2'] = np.array([0.1,0.2])
network['b3'] = np.array([0.1,0.2])
print_vec("重み1", network['W1'] )
print_vec("重み2", network['W2'] )
print_vec("重み3", network['W3'] )
print_vec("バイアス1", network['b1'] )
print_vec("バイアス2", network['b2'] )
print_vec("バイアス3", network['b3'] )
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
# 1層の総入力
u1 = np.dot(W1,x) + b1
# 1層の総出力
z1 = sigmoid(u1)
# 2層の総入力
u2 = np.dot(W2,z1) + b2
# 2層の総出力
z2 = sigmoid(u2)
# 出力層の総入力
u3 = np.dot(W3,z2) + b3
# 出力層の総出力
y = u3
print_vec("総入力1", u1)
print_vec("中間層出力1", z1)
print_vec("総入力2", u2)
print_vec("中間層出力2", z2)
print_vec("出力", y)
return y
# ネットワークのインスタンス化
network = init_network()
x = np.array([1.0,0.5])
y = forward(network, x)
print(y)
> *** 重み1 ***
[[0.1 0.2]
[0.3 0.4]
[0.5 0.6]]
shape: (3, 2)
*** 重み2 ***
[[0.1 0.2 0.3]
[0.4 0.5 0.6]]
shape: (2, 3)
*** 重み3 ***
[[0.1 0.2]
[0.3 0.4]]
shape: (2, 2)
*** バイアス1 ***
[0.1 0.2 0.3]
shape: (3,)
*** バイアス2 ***
[0.1 0.2]
shape: (2,)
*** バイアス3 ***
[0.1 0.2]
shape: (2,)
*** 入力 ***
[1. 0.5]
shape: (2,)
*** 総入力1 ***
[0.3 0.7 1.1]
shape: (3,)
*** 中間層出力1 ***
[0.57444252 0.66818777 0.75026011]
shape: (3,)
*** 総入力2 ***
[0.51615984 1.21402696]
shape: (2,)
*** 中間層出力2 ***
[0.62624937 0.7710107 ]
shape: (2,)
*** 出力 ***
[0.31682708 0.69627909]
shape: (2,)
(array([0.31682708, 0.69627909])
結果が得られました。
5. おわりに
本記事では、ニューラルネットワークの活性化関数の具体例を実装しながら、ニューラルネットワークの順伝播Pythonでの実装を実施しました。
引き続き、連載に沿って深層学習を学んでいきます。
連載記事目次
第1回:入力層・中間層
第2回:活性化関数(本記事)
第3回:出力層
第4回:勾配降下法
第5回:誤差逆伝播法
参考文献
この記事は以下の情報を参考にして執筆しました。
参考:ゼロから作るDeepLearning, O'REILLY社