本連載記事の概要
本連載記事では、全5回でDeepLearning(深層学習)をゼロから実装し、学ぶことを目的としています。
「深層学習」はなんとなく知っているけど使えない方、Pythonで動かせるけど中身がブラックボックスになっていて理解できていない方が、実際の実装を通してプログラムがどういう仕組みで動いているか理解でき、使いこなせるようになることを目指します。
連載記事目次
第1回:入力層・中間層
第2回:活性化関数
第3回:出力層
第4回:勾配降下法(本記事)
第5回:誤差逆伝播法
目次
1. 勾配降下法
2. 勾配降下法における学習率
3. 確率的勾配降下法(SGD)
4. ミニバッチ学習
5. おわりに
1. 勾配降下法
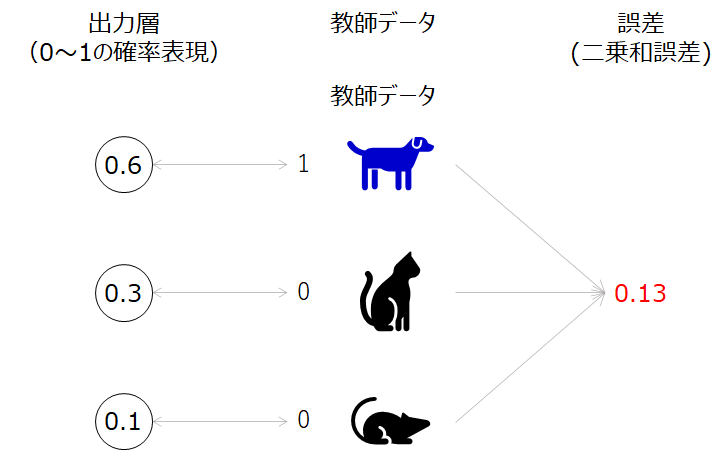
ディープラーニングでは、誤差関数を最小化するパラメータを求めて、精度のよい予測モデルを得ることが最終的な目的でした。この誤差関数は第3回で学んだように、二乗和誤差やクロスエントロピー誤差で求められますが、この誤差の値だけ見ていてもパラメータをどの方向に更新したらこの誤差を小さくできるか見当がつきません。
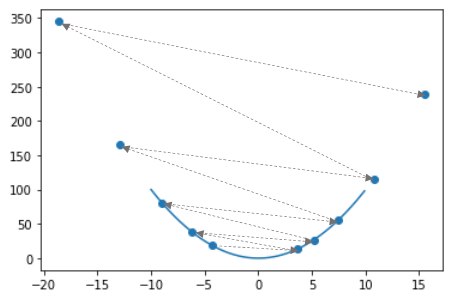
そこで活躍するのが、その点における傾きです。下の図のように傾きが分かれば得られた点からその傾きの方向に進むことで誤差関数の値を最も減らすことができます。
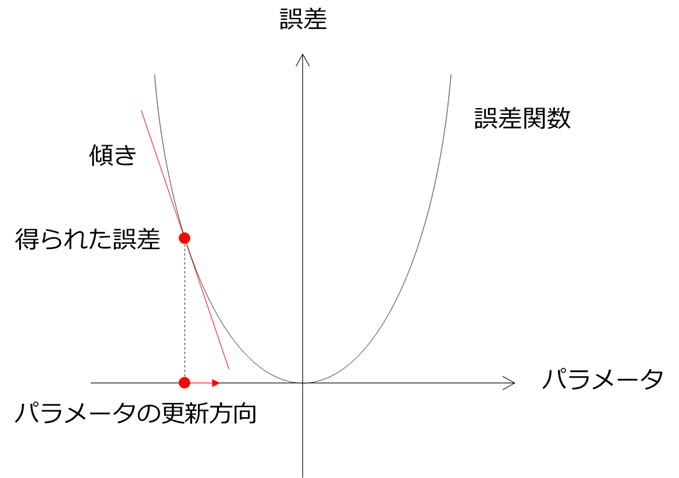
このように傾き(勾配)を利用して誤差関数の値を徐々に減らしていく方法を勾配降下法(gradient method)と呼びます。この勾配降下法は機械学習の最適化手法で非常によく用いられます。この勾配降下法を式で表すと、次の通りです。
w^{(t+1)}=w^{(t)}-\eta\nabla E\\
\nabla E=\frac{\partial E}{\partial \boldsymbol{w}}=\begin{bmatrix}\frac{\partial E}{\partial {w_1}}\cdots\frac{\partial E}{\partial {w_n}}\end{bmatrix}
この式におけるηは更新の量を表し、ニューラルネットワークの学習においては学習率(learning rate)と呼ばれます。1回の学習でどれだけパラメータを更新するか、を決めるのがこの学習率になります。この学習率は大きすぎても小さすぎてもうまく学習できません。このことについて、実例を交えて学んでいきます。
2. 勾配降下法における学習率
二次関数を例にとって考えていきます。
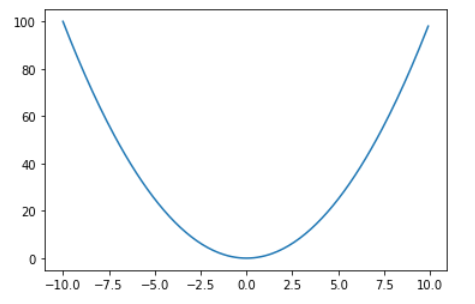
y = x^2
という関数があったとき、そのxとyの関係をグラフにすると次の通りになります。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
y = x**2
plt.plot(x,y)
この関数において、各xの点における傾きは、x^2の微分で求められるので、、
\nabla y=\frac{\partial y}{\partial x}=2x
となりますね。この微分して得られた傾きの式を用いて、xの初期値が与えられたときの学習の推移を見てみます。
def update(x_, lr, step_num):
x_update = []
y_update = []
for i in range(step_num):
grad = 2 * x_
x_ -= lr * grad
y_ = x_ ** 2
x_update.append(x_)
y_update.append(y_)
plt.scatter(x_update,y_update)
plt.plot(x,y)
return
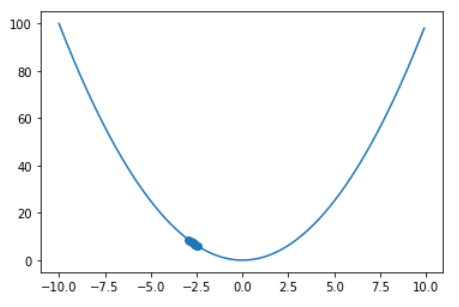
update(x_=-3, lr=0.1, step_num=10)
更新の推移をプロットで示しています。初期値-3から徐々に最小値に近づいていることが分かりますね。
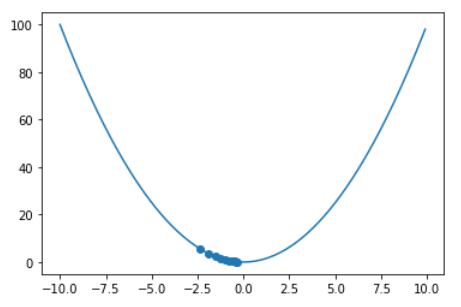
学習率を1/10に小さくしてみましょう。
update(x_=-3, lr=0.01, step_num=10)
先ほどのグラフと比較して、1回の更新量が少なくなってしまい、更新回数10回では最小値に辿り着けていません。
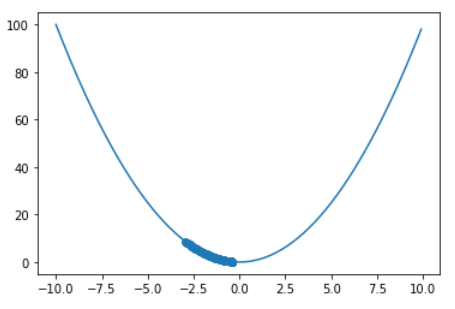
update(x_=-3, lr=0.01, step_num=100)
更新回数を増やせばなんとかなりそうです(=時間がかかるため計算コストが高くなる)。
次に学習率を大きくしてみましょう。
update(x_=-3, lr=1.1, step_num=10)
学習率が大きいと、最小値にたどり着くどころか、大きく発散しています。
ここまで学習率を変えたときの実例を示してきましたが、適切な学習率の設定が重要な問題になるということが分かりました。
3. 確率的勾配降下法(SGD)
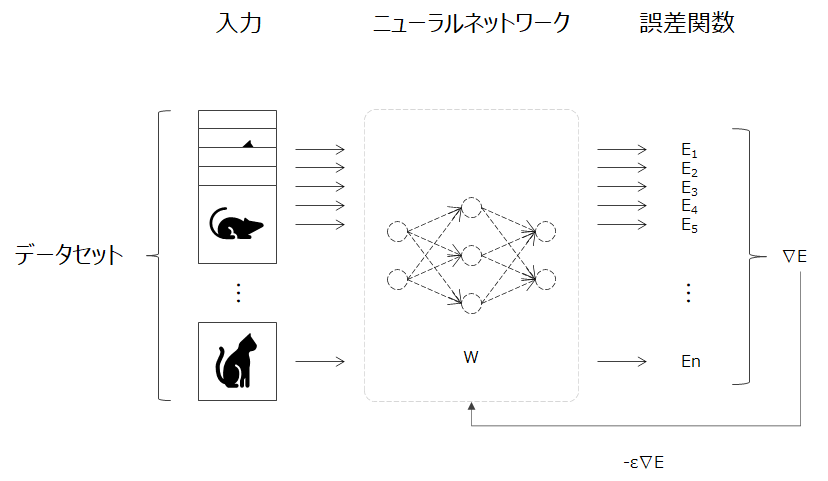
ニューラルネットワークの誤差関数を最小化するパラメータを見つける(最適化と呼ぶ)ために、勾配降下法が有効であることが理解出来ました。この勾配降下法は、全サンプルの勾配を利用しています。
ニューラルネットワークの学習は一般的に大量のデータが用いられるため、1回のパラメータの更新毎に全サンプルの勾配を求めていると計算に時間がかかってしまいます。
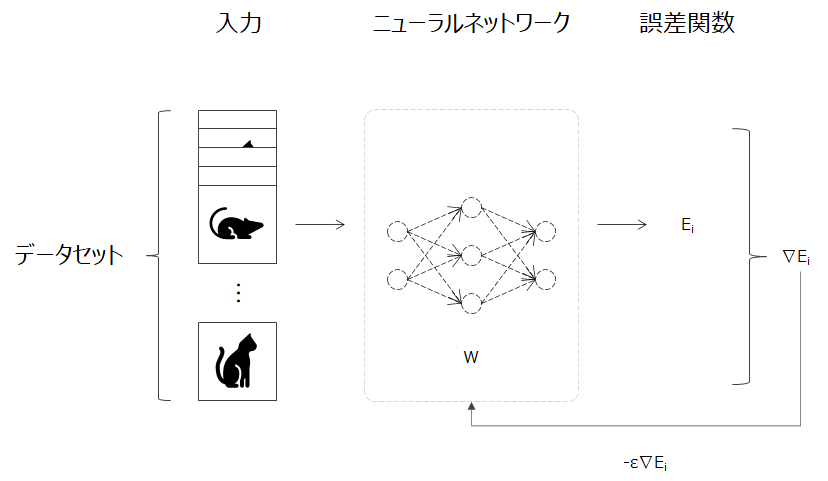
そこで考えられたのが確率的勾配降下法(SGD:Stochastic gradient descent)になります。この確率的勾配降下法では、確率的(ランダム)に抽出したサンプル(i番目)の誤差と勾配を求めパラメータを更新していくことを繰り返します。
この手法により計算コストが軽減されます。それだけでなく、局所極小解に収束するリスクが軽減される、オンライン学習(学習中にも追加のデータが入りパラメータが更新される)にも適用できるなど様々なメリットがあります。
4. ミニバッチ学習
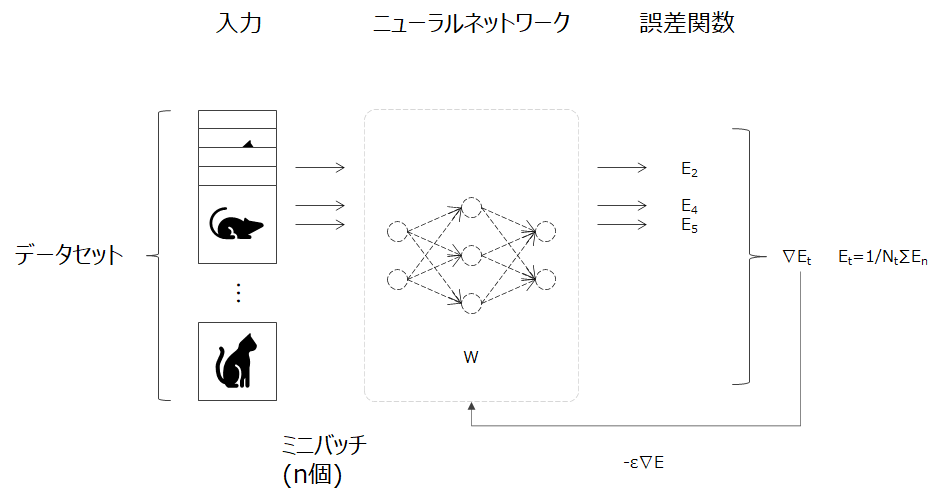
確率的勾配降下法と同様に、効率的なパラメータ更新の手法の一つにミニバッチ学習があります。ミニバッチ学習とは全データの中からミニバッチ(少数のデータのかたまり, n個のデータ)を無作為に選びだし、そのミニバッチに属するデータに対して学習を行います。
このミニバッチ学習で利用されるのは、ミニバッチのデータの平均誤差とその勾配です。式で表すと次のようになります。
w^{(t+1)}=w^{(t)}-\eta\nabla E\\
E_t=\frac{1}{N_t} \sum_{n}E_n\\
このミニバッチ学習を用いることで、確率的勾配降下法と同様に計算コストが軽減されます。加えてミニバッチ化による、並列処理により、コンピュータのリソースを有効活用できるため効率的に学習を進めることができます。
5. おわりに
本記事では、ニューラルネットワークのパラメータ更新に必要な勾配降下法を学びました。最終回では、この勾配降下法に用いた勾配を求める方法を学びニューラルネットワークの学習を完成させていきます。
連載記事目次
第1回:入力層・中間層
第2回:活性化関数
第3回:出力層
第4回:勾配降下法(本記事)
第5回:誤差逆伝播法
参考文献
この記事は以下の情報を参考にして執筆しました。
参考:ゼロから作るDeepLearning, O'REILLY社