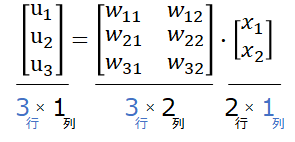本連載記事の概要
本連載記事では、全5回でDeepLearning(深層学習)をゼロから実装し、学ぶことを目的としています。
「深層学習」はなんとなく知っているけど使えない方、Pythonで動かせるけど中身がブラックボックスになっていて理解できていない方が、実際の実装を通してプログラムがどういう仕組みで動いているか理解でき、使いこなせるようになることを目指します。
連載記事目次
第1回:入力層・中間層(本記事)
第2回:活性化関数
第3回:出力層
第4回:勾配降下法
第5回:誤差逆伝播法
目次
1. パーセプトロン
2. ニューラルネットワーク(多層パーセプトロン)
3. 入力層・中間層の数式化
4. バイアスの追加
5. Pythonによる実装
6. おわりに
1. パーセプトロン
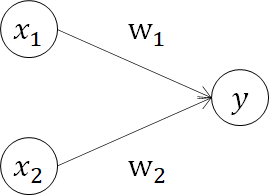
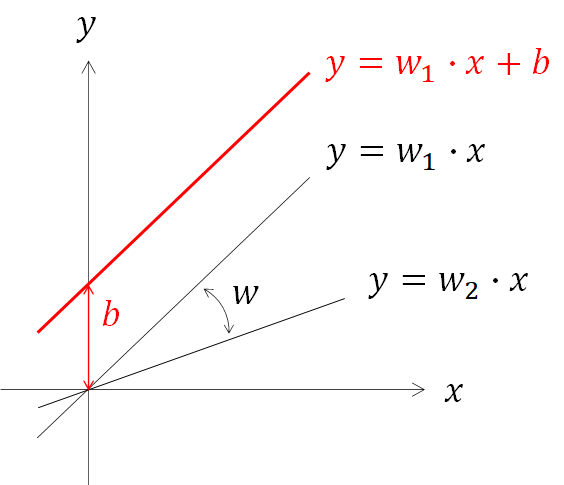
人間の脳内にあるニューロン(神経細胞)の構造モデルを模した最も単純なアルゴリズムをパーセプトロン(人口ニューロン、単純パーセプトロン)と呼び、ある入力(x1, x2)に対して出力(y)を出す機能を持っています。
この出力(y)は、入力信号に対して、発火する(信号を流す, 1)か、発火しない(信号を流さない, 0)の二値です。
ここで、wを重み、θを閾値と呼びます。入力に対して重みをかけて得られた数値で、0、1を判定しているわけですね。この0、1判定を精度よく行うために、パラメータwをチューニングしていくことを学習と呼んでいます。
\begin{equation}
y =
\left\{ \,
\begin{aligned}
& 0 (w_1 \cdot x_1 + w_2 \cdot x_2 ≦ θ) \\
& 1 (w_1 \cdot x_1 + w_2 \cdot x_2 > θ) \\
\end{aligned}
\right.
\end{equation}
但し、このニューロンは構造が単純であるため表現力が乏しく、非線形問題などの複雑な問題を解けないといった問題があります。
2. ニューラルネットワーク(多層パーセプトロン)
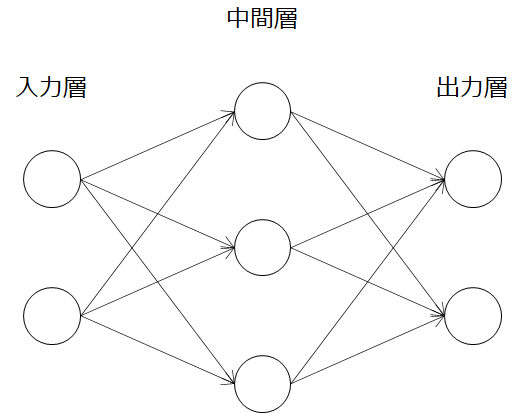
そこで、考えられたのがパーセプトロンを多層にしたニューラルネットワーク(多層パーセプトロン)です。基本的には入力層、中間層(隠れ層)、出力層という構造を持ちます。この図では中間層が1層ですが、より表現力を高めるために何層も重なねられたものをディープニューラルネットワークと呼び、その中の重みを学習させて精度を高めることをディープラーニング(深層学習)と呼んでいます。
本記事では、この入力層と中間層について詳しく見ていきます。
3. 入力層・中間層の数式化
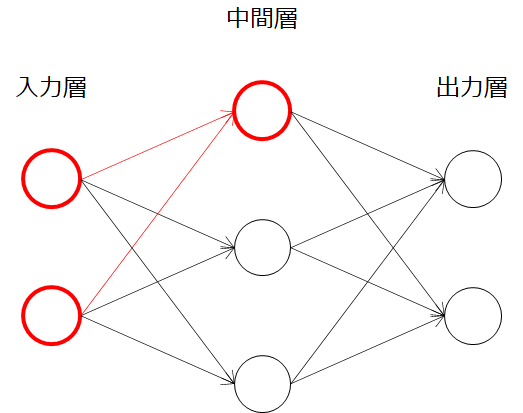
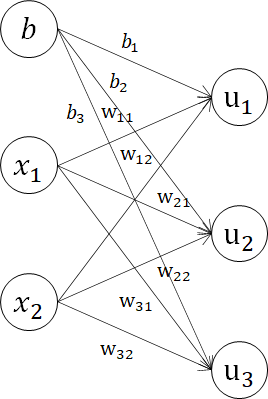
まずは、パーセプトロンの例に倣って、ニューラルネットの構造を数式で表していきましょう。ここで、ニューラルネットワークの入力層、中間層の一部(赤色の部分)を見ると、パーセプトロンの構造に非常によく似ていることが分かります。パーセプトロンの出力yだった部分が、中間層の一つになっているわけですね。
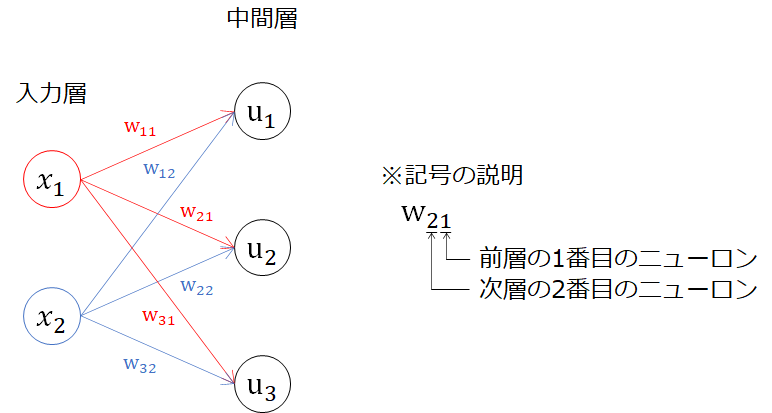
パーセプトロン同様、図に変数を入れていきます。今回は、中間層までですのでyと区別して、uを用いています。
u_1 = w_{11}x_1 + w_{12}x_2 \\
u_2 = w_{21}x_1 + w_{22}x_2 \\
u_3 = w_{31}x_1 + w_{32}x_2 \\
ここで、行列の内積の定義を思い出してみます。※参考:線形代数I/内積
a =
\begin{bmatrix}
a_1 \\
a_2 \\
\vdots \\
a_n
\end{bmatrix},\quad b =
\begin{bmatrix}
b_1 \\
b_2 \\
\vdots \\
b_n
\end{bmatrix}\\
a \cdot b = a_1b_1 + a_2b_2 + \cdots + a_nb_n = \sum_{i=1}^{n} a_ib_i
なんとなく行列の内積と形が似ていることが理解できたでしょうか。例えば、u1をこの行列の内積で表してみると、
u_1 =
\begin{bmatrix}
w_{11} & w_{12}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix} (= w_{11}x_1 + w_{12}x_2)
になります。同様に、u2、u3を行列の内積表現すると、
u_1 =
\begin{bmatrix}
w_{11} & w_{12}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix}\\
u_2 =
\begin{bmatrix}
w_{21} & w_{22}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix}\\
u_3 =
\begin{bmatrix}
w_{31} & w_{32}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix}
です。x1、x2が共通していて、中間層のu、重みwも行列表現が出来そうです。つまり、
\begin{bmatrix}
u_1 \\
u_2 \\
u_3
\end{bmatrix} =
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix}\\
となり、より一般的な形で表すと、
\boldsymbol{u} = \boldsymbol{W} \boldsymbol{x}
と表されます。
行列の積の決まりごとも守られています。ここまで、出力層から中間層は行列の内積で表現できることを確認しました。
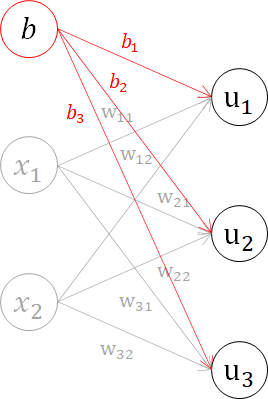
4. バイアスの追加
ここまで、入力層と中間層を数式化しました。次にバイアスを加えていきます。重みwのみで表現だと、原点が固定され傾きの影響しか反映できない一方で、バイアスが存在することで軸方向のずれの影響を持たせることができます。
3章までと同様、数式と行列表現をしてみます。
u_1 = w_{11}x_1 + w_{12}x_2 + b_1 \\
u_2 = w_{21}x_1 + w_{22}x_2 + b_2 \\
u_3 = w_{31}x_1 + w_{32}x_2 + b_3 \\
\begin{bmatrix}
u_1 \\
u_2 \\
u_3
\end{bmatrix} =
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix} +
\begin{bmatrix}
b_1 \\
b_2 \\
b_3
\end{bmatrix}
\boldsymbol{u} = \boldsymbol{W} \boldsymbol{x} + \boldsymbol{b}
ここまで、出力層から中間層までを数式で表現していきました。次にプログラムでの実装に移ります。
5. Pythonによる実装
前章まで扱ってきたニューラルネットワークの入力層~出力層を実装します。取り扱う構造は、以下の単層(入力層~中間層)・複数ユニット(中間層3ノード)のモデルです。
\begin{bmatrix}
u_1 \\
u_2 \\
u_3
\end{bmatrix} =
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32}
\end{bmatrix} \cdot
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix} +
\begin{bmatrix}
b_1 \\
b_2 \\
b_3
\end{bmatrix}
\boldsymbol{u} = \boldsymbol{W} \boldsymbol{x} + \boldsymbol{b}
# 重み
W = np.array([
[0.1, 0.2],
[0.2, 0.3],
[0.3, 0.4],
])
print(W.shape)
> (3, 2)
# バイアス
b = np.array([0.1, 0.2, 0.3])
print(b.shape)
> (3,)
# 入力値
x = np.array([1.0, 5.0])
print(x.shape)
> (2,)
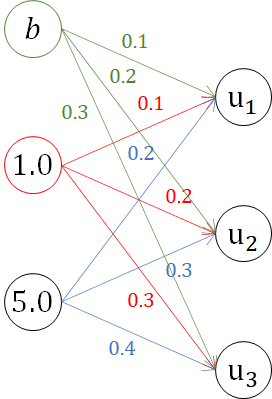
先ほどの図に数字を入れてみるとこんな感じです。
手計算も可能なので、一度計算しておきます。
u_1 = w_{11}x_1 + w_{12}x_2 + b_1 = 0.1*1.0+0.2*5.0+0.1=1.2\\
u_2 = w_{21}x_1 + w_{22}x_2 + b_2 = 0.2*1.0+0.3*5.0+0.2=1.9 \\
u_3 = w_{31}x_1 + w_{32}x_2 + b_3 = 0.3*1.0+0.4*5.0+0.3=2.6 \\
それではプログラムで計算させてみましょう。行列の内積はnumpyのdotメソッドで計算することができます。
u = np.dot(W, x) + b
print(u)
> [1.2 1.9 2.6]
結果が一致しました。
6. おわりに
本記事では、ニューラルネットワークの入力層から中間層の処理を数式で追いながらPythonでの実装を実施しました。
引き続き、連載に沿って深層学習を学んでいきます。
連載記事目次
第1回:入力層・中間層(本記事)
第2回:活性化関数
第3回:出力層
第4回:勾配降下法
第5回:誤差逆伝播法
参考文献
この記事は以下の情報を参考にして執筆しました。
参考:ゼロから作るDeepLearning, O'REILLY社