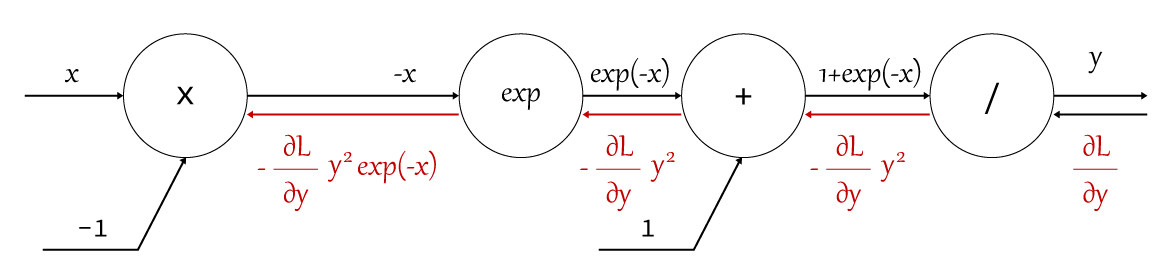概要
最近のもっぱらの興味はディープラーニングです。
UnityにもML Agentというプラグインがあったり、最近見るニュースが猫も杓子もディープラーニングによるものだったりと、機械学習、とりわけディープラーニングについては知らないとならないなというのをヒシヒシと感じています。
ということで、ディープラーニング自体の基礎から学習しようと本を手に取って勉強中です。
勉強には以下の本を熟読させてもらっています。
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
今回はいきなりディープラーニングについて触れるのではなく、本の中で語られている「計算グラフ」についてまとめようと思います。
なぜこれだけをピックアップしたかというと、微分という計算をグラフ化することでとても簡単に行えるという点がまず面白かったところ。
そして(この本の中では)この「計算グラフ」を元に機械学習を進めていくので、そのためのまとめを別にしようと思ったのも理由のひとつです。
ディープラーニング自体については別途記事を書いているので、後日公開予定です。
誤差逆伝播法
計算グラフの説明の前に。
書籍の説明によると、ニューラルネットワークの学習にはその過程において、算出された出力(とある画像になにが描かれているか、などの判定などの出力結果)を「勾配降下法」を用いて最適化していきます。
(この詳細については後日の記事で触れます)
その際、勾配を求めるために微分を行うわけですが、書籍の前半では「数値微分」を用いて実装を行っていました。
(ちなみに、偏微分と勾配の関係は以前記事に書いたので興味があったら読んでみてください→「偏微分(勾配)が法線を表すイメージ」)
しかし計算処理の効率から、時間がかかるという難点があります。
そこでこの「誤差逆伝搬法」を用いることで、効率的かつ高速に計算を行おう(学習を行おう)というのが目的です。
この書籍によると、誤差逆伝搬法を理解するのに、一般的な書籍や文献では「数式」によって話が展開されるそうです。
しかし、この本の著者は「視覚的」にこの手法を捉えることに、つまりくだんの「計算グラフ」を用いることにより理解が進むと考えて解説に採用したそうです。
本記事は前述のように、この「計算グラフ」自体がとても面白かったのでそれだけをまとめた記事になります。
計算グラフ
計算グラフとは
計算グラフとは、(前述のように)計算の過程をグラフで「視覚化」して表したものです。
計算グラフは複数の「ノード」と「エッジ」によって表現されます。
(エッジはノード間をつなぐ直線として表されます)
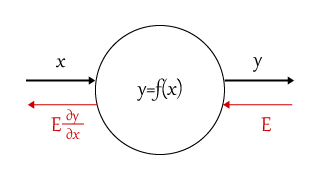
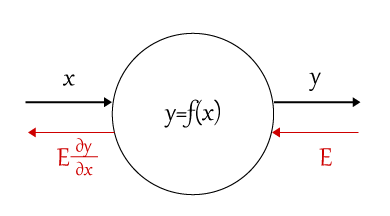
図にすると以下のイメージ。
図の意味は、$x$が入力で$f(x)$という関数を通すと$y$という出力になる、ということを示しています。
また赤字で書かれた部分は(このあと説明する)誤差逆伝搬法による入力と出力の関係を表しています。
(逆と名前がつく通り、入力と出力の方向が逆になっています)
逆伝搬法では$E$が入力、$E\frac{\partial y}{\partial x}$が出力です。(とある関数$f(x)$の微分を行った結果を乗じたものです)
計算グラフで解く
計算グラフとは一体どんなものなのか。
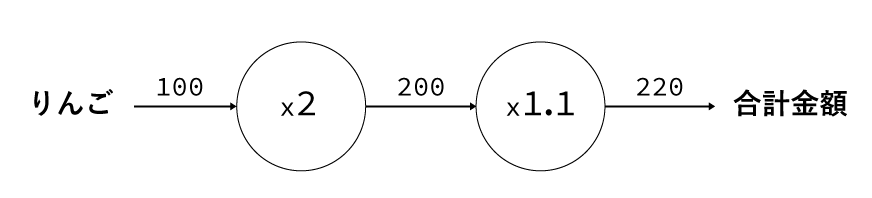
以下の図を見てみてください。内容自体はごく簡単な買い物の計算の例ですが、計算グラフをどう使うのか、というのはイメージしてもらえるかと思います。
上のグラフでは、ひとつ100円のりんごを2つ買い、消費税が10%のときの合計金額を表しています。
グラフの意味としては、x2やx1.1の部分が乗算ノードとなり、入力として100円が渡されます。
そして左から右へと順にデータが流れていくことで最終的な合計金額が算出できる、という具合になっています。
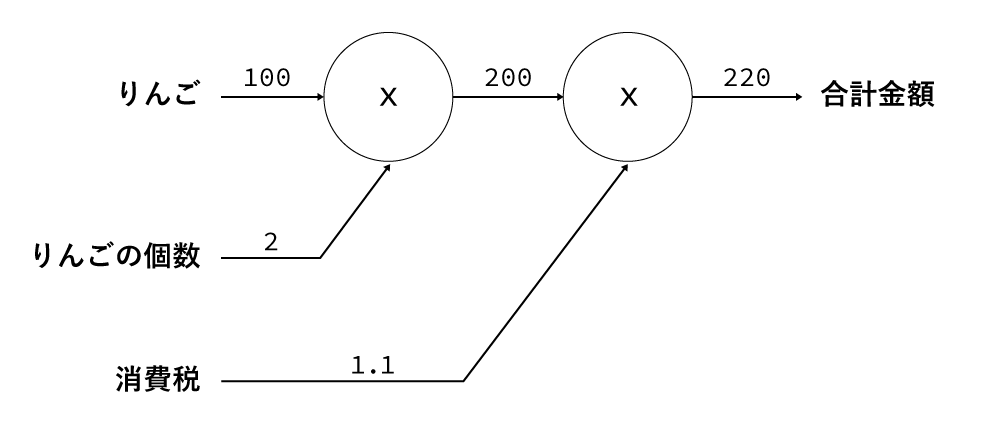
さらに、以下のように「2個」や「1.1」なども入力として扱い、x2ではなくxだけを表すノードとして表現することもできます。
その場合は以下の図のようになります。
さてでは、もう少しだけグラフを複雑にしてみます。
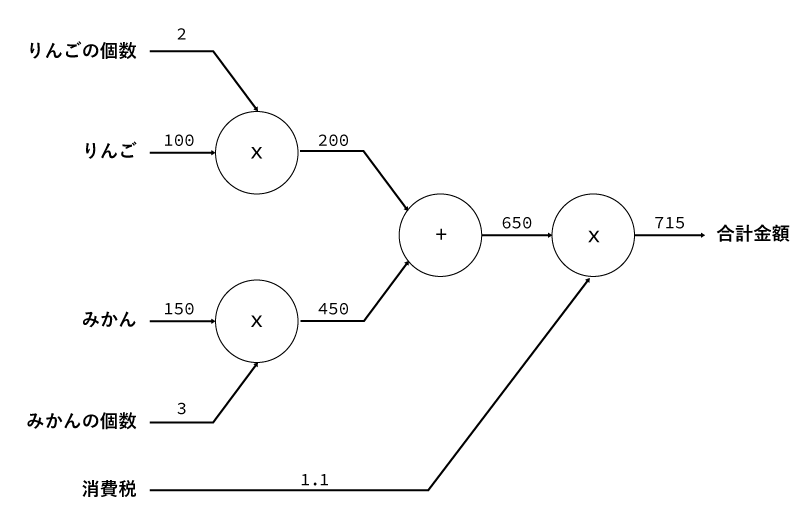
りんごだけではなく、みかんも買ったとしましょう。みかんはひとつ150円で3個買いました。
するとグラフは以下のようになります。
いかがでしょうか。
りんごの数やりんごの値段などが「入力」となり、それを各ノードを「左から右に」流れていくことで計算が行えているのが分かるかと思います。
局所的な計算
計算グラフを用いることのメリットのひとつは「計算の局所性」です。
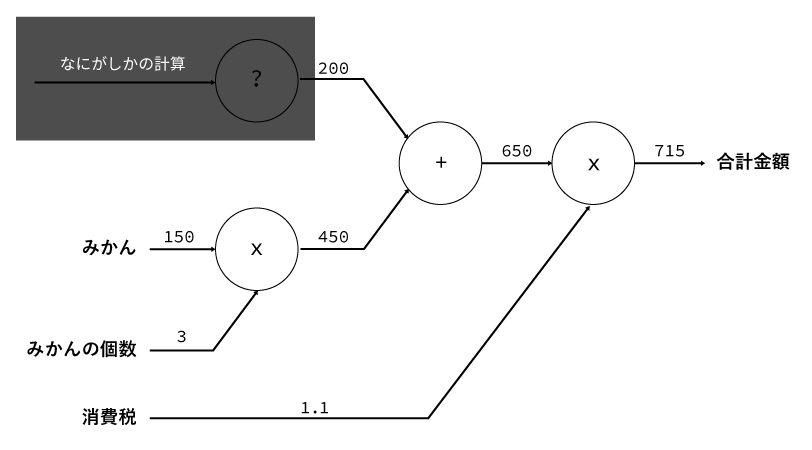
例えば、上の図の例にすると、「りんごの買い物」部分の計算をまるっとブラックボックス化して「なにがしかの計算を行った結果」として200円という結果が渡ってきたとしても計算を行うことができます。
図にすると以下のようになります。
見て分かるように、「りんごの買い物」部分の計算をブラックボックス化しても「みかんの買い物の計算」には影響がないことが分かります。
つまり、「入力に対して計算を行い、出力を行えばいい」という局所性が生まれるのです。
(上の例では、入力された200と450を「足す」だけでいいというわけですね)
上で書いた図のように、複雑な大きな計算がある場合でも、局所的に見ればただの足し算掛け算などのシンプルな計算として表現できます。
そして、その局所的な計算部分だけに絞って逆伝播を計算することで、そしてそれをレイヤー化し局所的に計算できるようにすることで、機械学習の勾配を効率よく計算していく、という手法になります。(と解釈しています)
計算グラフを使う意味
なぜ計算グラフを使うといいのでしょうか。
その答えは前述の「局所性」にあります。
特に、今回達成しようとしていることは「ディープラーニング」を用いて機会に学習をさせることです。
そしてその学習法として「勾配降下法」が用いられるというのは前述した通りです。
さらに勾配を求めるための数値計算(微分)が効率が悪く、それをより効率よく解くというのが目的でした。
つまりこの「勾配を求める」、具体的には「微分を求める」ことを効率的に行いたいわけです。
そしてここに、「逆伝搬法」の「逆」たる所以があるのですが、今見てきた計算は「順方向」の計算です。
これを「逆」にすることで「逆伝搬法」を実現することができるのです。
さてでは具体的にはどういうことなのか。
今、上のグラフで計算したのはりんごとみかんの買い物の合計金額を求めるものでした。
もし仮に、りんごの値段が値上がりした場合、最終的な合計金額にどのように影響するかを見てみることでイメージしてみてください。
ちなみにこの「最終的な金額にどう影響するか」は「りんごの値段に関する支払い額の微分」を求めることに相当します。
記号にすると、りんごの値段を$x$、合計金額を$L$として、
\frac{\partial L}{\partial x}
と表現することができます。
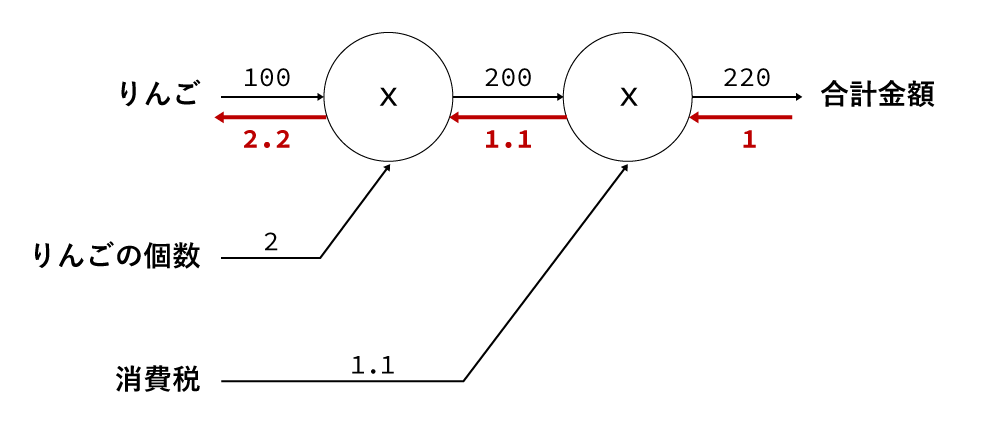
これを実際に図にすると以下のようになります。
上の図で示した通り、逆順の計算については赤文字で表現しました。(冒頭の説明の図を思い出してください)
逆伝搬は「局所的な微分」を逆順にノードに渡していき、最終的な結果を得るものです。
計算の結果から、「りんごの値段」が変わると合計金額に2.2倍の影響があることが示されているわけです。
試しにりんごが100円から200円、つまり100円値上がりしたとしましょう。
すると、上の計算グラフの結果から、合計金額には2.2倍の影響がある、ということがすでに分かっているので、100円の2.2倍、つまり220円値上がりする、というのがすぐに計算できます。
実際にそうなるか計算してみましょう。
100 * 2 * 1.1 = 220
200 * 2 * 1.1 = 440
具体的に計算しなくても最終的な合計金額が220円変化することが分かりました。
また、計算グラフを用いることのメリットは、(今回の例ではりんごの値段だけを対象にしましたが)消費税が変化した場合や買う個数が変化した場合にもどのように変化するかがすでに示されています。
つまり、微分の途中結果を共有することができる、というのも計算グラフを用いるメリットです。(そしてこれが計算効率を高めてくれる理由でもあります)
試しに「りんごの個数」でもやってみましょう。
りんごの個数は合計金額に対して1.1倍の影響があると示されています。
りんごひとつの値段は100なので、3個になった場合は100の1.1倍、つまり110の影響となるわけですね。
なので、2個のときは220なので、3個の場合は110円の値上がりになる、というのが分かります。
上のサンプルは日常でも暗算で行っているような内容なので恩恵をあまり感じられないかもしれませんが、これが例えばたくさんの買い物だったり、ローンの計算だったりなど複雑な計算を重ねた結果をグラフ化したものだった場合はとても有意義なものになることが想像できるかと思います。
念の為これを一般化しておくと、冒頭の図を再掲すると以下のようになります。
右に書かれた$E$が入力で、ノードに応じた微分計算を行い、左に流していくということが示されています。
上の実際の計算グラフと照らし合わせて見てみてください。
計算グラフの逆伝播
順方向への計算はノードをつなぐ演算の種類によって計算を行い、その出力結果を次のノードへと伝播していきました。
やっていることは日常生活で行っているような計算をそのまま次のノードへ伝えるだけなのでイメージしやすかったと思います。
今度はその逆伝播です。
逆伝播では、上記の順方向への計算結果を逆にたどります。
そして順方向での出力は入力になります。
逆伝播では、その入力(順方向の出力)を最初に受け取り、以前のノードグラフの計算方法に基づいた「微分」を計算して(順方向とは逆の)次のノードへと計算結果を渡していきます。
連鎖律
上の図で説明してきたことは、いくつもの計算(関数)を行う場合、それをグラフとして表現し、局所的な計算をノードという単位に分解して行うというものでした。
そしてそれの逆伝搬(微分)を行うことで全体の微分が行えることも示しました。
この伝達する原理は連鎖律によるものです。
Wikipediaから引用させてもらうと以下のように記載されています。
微分法において連鎖律(れんさりつ、英: chain rule)とは、複数の関数が合成された合成関数を微分するとき、その導関数がそれぞれの導関数の積で与えられるという関係式のこと。
このことから、各計算(関数)をノードに分解しそれぞれの微分の積を計算して微分を行おう、というのが計算グラフだと言うことができると思います。
合成関数
合成関数とは複数の関数によって構成される関数のことです。
例えば、$z = (x + y)^2$という式は、
z = t^2 \\
t = x + y
というふうに分解して考えることができます。
前述のように、元の関数の導関数が、複数の関数の導関数の積として求められるわけです。
試しに上記の合成関数の微分の積を考えてみましょう。
z = t^2 \\
\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \frac{\partial t}{\partial x}
やや複雑に見えますが、やっていることはシンプルです。
まず、$t = x + y$の偏微分を表すのが$\frac{\partial t}{\partial x}$ですね。($x$による偏微分)
そして、$z = t^2$の偏微分を表すのが$\frac{\partial z}{\partial t}$です。
これを掛けると$\partial t$が「打ち消し合う」ため、結果として$\frac{\partial z}{\partial x}$が得られる、というわけです。
大本の結果を得るためには(つまり$\frac{\partial z}{\partial x}$を得るためには)、結局の所それぞれの関数の微分を計算しないとなりません。
しかし、この分解こそが重要なのです。
なぜなら、計算グラフで考えた場合に、順方向への計算グラフで得た出力を保持しておき、逆順の場合は保持した出力結果を用いて微分を計算し、次の(順方向のときは前の)ノードへそれを渡すだけでよくなるからです。
前述の局所性ですね。
つまり大局的に計算を見なくとも、自分の見える範囲だけを計算してやればよくなるため、一見複雑に見える関数の微分も比較的簡単に求めることができる、というわけです。
冒頭で書いたように、この性質がとても面白いなと思ったのが計算グラフだけを取り上げた理由です。
ディープラーニングでは色々な関数が登場します。(シグモイド関数とかReLU関数とか)
それを真面目に微分していくととても大変ですが、この「合成関数」という観点から計算をノードに分解、それを元に微分を行うことで目的の微分(出力)を得ることができる、というのが計算グラフを使うメリットです。(と理解しています)
各ノードを「レイヤー」として実装する
さて、実際の実装についての話です。
プログラムで表現する場合、上で説明した各ノードは「レイヤー」という概念で実装を行います。
そしてそれを連結していくことで計算グラフを構築していきます。
ひとつ簡単なコード例を示すと以下のようになります。
(冒頭の書籍から引用させていただきました)
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
"""
順伝搬
引数を乗算し、引数を保持しておく(逆伝搬で利用する)
"""
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
"""
逆伝搬
doutは順方向ノードの出力の微分(d out)
"""
dx = dout * self.y # xとyをひっくり返して返す
dy = dout * self.x
return dx, dy
これらの詳細な内容はぜひ、紹介した書籍を読んでみてください。
非常に分かりやすく、また「ゼロから」の名前の通り、最低限の算術ライブラリ以外はすべてスクラッチで実装されているのでブラックボックスがなく、「ディープラーニングとはなにか」を体感できる良書となっています。
各レイヤーの逆伝搬
計算グラフの内容は以上です。
あとは逆伝搬の計算がどうなるのか、それぞれのレイヤーの逆伝搬についてまとめて終わりにしたいと思います。
加算レイヤーの逆伝搬
加算レイヤー(加算ノード)の式は以下で表されます。
z = x + y
これを偏微分すると以下が得られます。
\frac{\partial z}{\partial x} = 1 \\
\frac{\partial z}{\partial y} = 1
偏微分はそれぞれの変数についてだけ微分を行い、それ以外を定数と見なして微分を行う方法です。
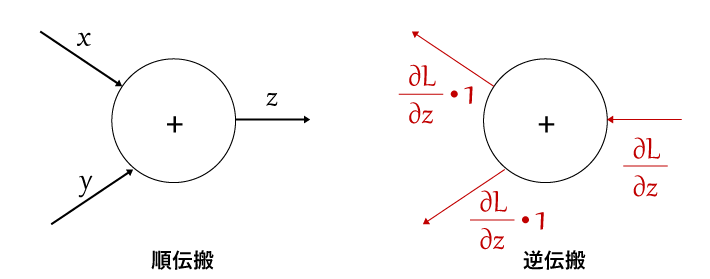
そのため、上記のようにどちらも1になり、結果的に逆伝搬では入力をそのまま伝搬することになります。
逆伝播では入力に対して1を乗算して次のノードに流している様子が分かります。
実際には1の乗算はなにも変化しないので入力をそのまま出力するだけですね。
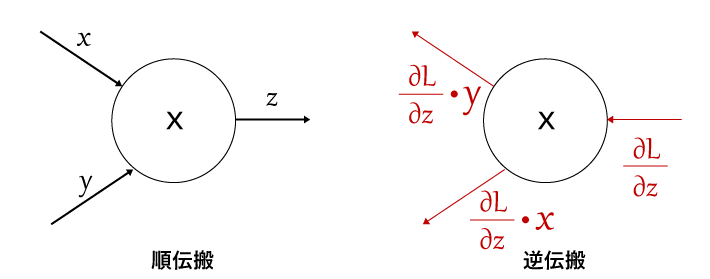
乗算レイヤーの逆伝搬
次は乗算レイヤーの逆伝搬です。
加算と同様、式を先に書くと以下のようになります。
z = x * y
\frac{\partial z}{\partial x} = y \\
\frac{\partial z}{\partial y} = x
これはつまり、逆伝搬の入力に対して$x, y$をひっくり返して乗算したものを出力する、ということです。
乗算レイヤーの場合は入力に対して、(順伝播では)$x$の入力だったほうに$y$を乗算し、$y$の入力だったほうには$x$を乗算して流しているのが分かるかと思います。
シグモイドレイヤーの逆伝搬
シグモイド関数
シグモイドレイヤーは、シグモイド関数を表すレイヤーです。
シグモイド関数とは、ニューラルネットワークにおいて「活性化関数」に使われる関数です。
ざっくりとした説明をすると、各ニューロンを流れた信号が次のニューロンへ出力するかしないかを決めるための関数です。(なので「活性化」関数)
シグモイド関数は以下で表される関数です。
y = \frac{1}{1 + exp(-x)}
ここでの$exp$は自然数$e$を底とする指数関数です。($e^{-x}$)
つまり、$1 + exp(-x)$の逆数が関数の結果となります。
実は計算グラフの中でここが書きたくてこの記事を書いたようなものですw
シグモイド関数をWikipediaから引用させてもらうと、
シグモイド関数は、生物の神経細胞が持つ性質をモデル化したものとして用いられる。
シグモイド (英: sigmoid) とは、シグモイド曲線 (英: sigmoid curve) ともいい、ギリシャ文字のシグマ(語中では σ だがここでは語末形の ς のこと)に似た形と言う意味である。ただし、単にシグモイドまたはシグモイド曲線と言った場合は、シグモイド関数と似た性質を持つς型の関数(累積正規分布関数、ゴンペルツ関数、グーデルマン関数など)を総称するのが普通である。
実際に関数をグラフにプロットしてみるとその意味が分かると思います。
グラフにすると以下のようになります。

記号「ς」に似た形、というのも頷けますね。
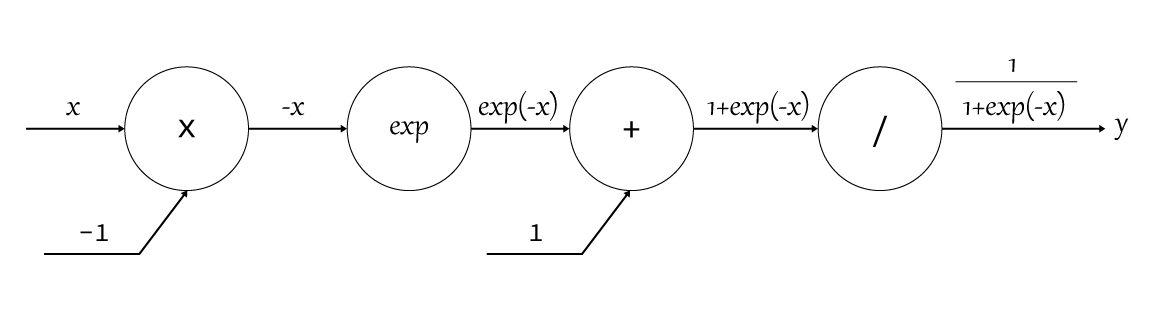
さて、これを計算グラフで表してみると以下のようになります。
「/」ノードと「exp」ノードの微分
新しく、「/」ノードと「exp」ノードが出てきました。
「/」のノードはつまりは$y = \frac{1}{x}$を計算するノードです。
微分の公式から以下のように求めることができます。
\begin{eqnarray}
\frac{\partial y}{\partial x} &=& - \frac{1}{x^2} \\
&=& -y^2
\end{eqnarray}
ここで、$y = \frac{1}{x}$なので、$-\frac{1}{x^2}$は$-y^2$となります。
これはつまり、逆伝搬のときは入力に対して$-y^2$を乗算して次のノードに伝えるという意味になります。
(実際の実装では順伝播の出力$y$を保持しておき、逆伝播のときはそれを2乗してマイナスを掛けたものを入力に乗じて出力とします)
次に「exp」ノードです。
「exp」ノードは$y = exp(x)$を表します。ここでの$exp$は自然数$e$の指数関数です。
そのため、微分しても同じ$exp(x)$となります。(自然数の性質)
つまり、
\frac{\partial y}{\partial x} = exp(x)
となります。
これは、逆伝搬のときは入力に対して$exp(-x)$を掛けて次のノードに渡すことになります。
それを踏まえてグラフに書きあわらしてみると以下のようになります。
一見複雑に見えるシグモイド関数の微分も、計算グラフを用いることで「局所的な計算」の積で表すことができました。
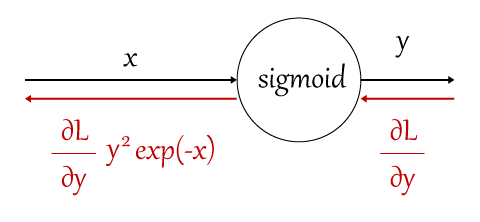
実際に使う場合には以下のように「シグモイドレイヤー」としてグループ化して計算を行うことができます。
ディープラーニング(ニューラルネットワーク)ではこうした微分を使って学習を進めていきます。
計算グラフについては以上です。
ディープラーニング自体については後日公開予定の記事で書こうと思います。
参考記事
以下の記事も計算グラフについて言及しているので合わせて読んでみると理解が深まるかもしれません。