RICAPのパラメーターをコサインカーブでゆらして更に使い倒す #Python

RICAP¹というData Augmentationがあります。これは単体でもかなり効果が高いのですが、パラメーターのベータをコサイン曲線でスケジューリングすると更に精度がよくなるんじゃない？と思って確かめてみました。結果は、1から訓練する場合はほぼ上がることを確認できました。

MobileNetでの転移学習では、コサインカーブの効果は際どかったですが一応上がり、CIFAR-10の精度で95.29%を達成することができました。

RICAPのパラメーター

RICAPとはこのように4枚の画像のパッチをつなぎ合わせて、1枚の画像を作るData Augmentationです。例えば、アニメのキャラの顔の分類をする問題で、通常は初音ミクの画像は初音ミクとして、博麗霊夢の画像は博麗霊夢として訓練させます。

RICAPはちょっと変わったことしていて、まずクラス関係なく4枚の画像を取ってきます。そこからランダムにクロップして²、その4枚をつなぎあわせます。そして、その面積比で新しいラベルを合成します。4枚のクロップの面積比が、例えばミク：霊夢が0.8：0.2なら、合成された画像は「80%ミク、20%霊夢」の画像となります³。

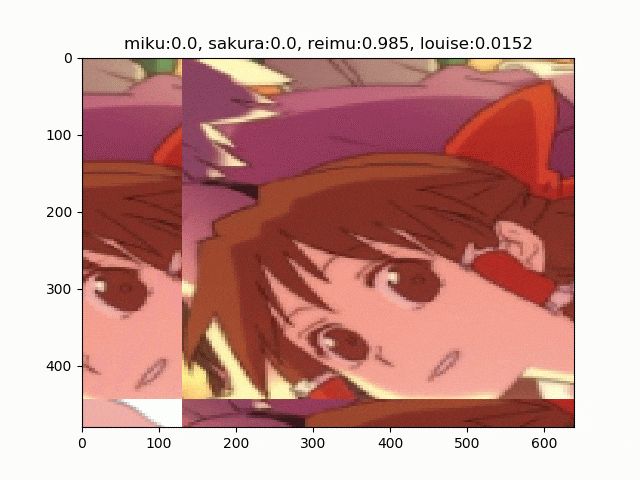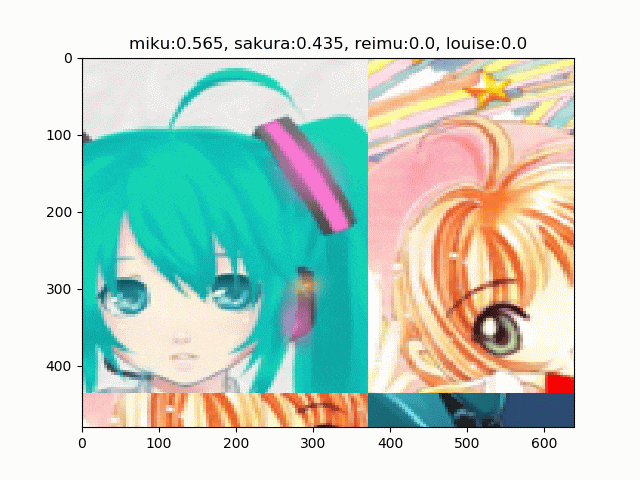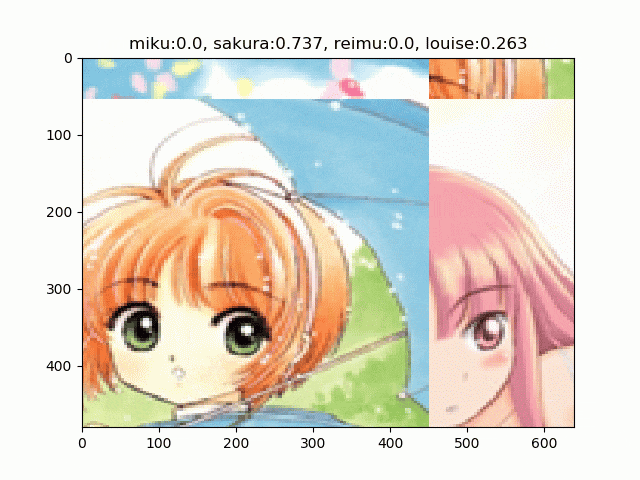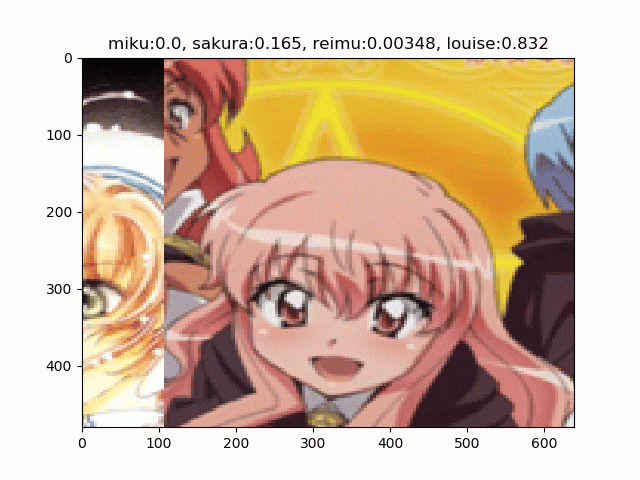
文章で説明するより実物を見たほうが早いのでこちらをどうぞ。初音ミク、木之本桜、博麗霊夢、ルイズの画像をRICAPで合成しています⁴。

RICAPには$\beta$という（ハイパー）パラメーターがあります。これは4つの画像パッチのサイズを決めるのに使われます。

{w = \text{round}(w^{'}I_x), \hspace{5pt}h = \text{round}(h^{'}I_y), \\
w^{'} \sim Beta(\beta,\beta), \hspace{5pt}h^{'} \sim Beta(\beta,\beta)
}

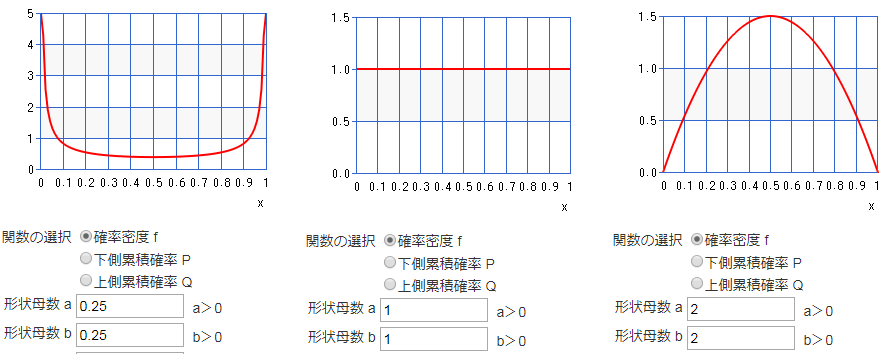
ここで$w, h$は左上のパッチの幅と高さ、$I_x, I_y$は元の画像の幅と高さです。$w', h'$はベータ分布から発生させます。ベータ分布というと仰々しく聞こえますが、xが0～1で一様分布から正規分布に近いような分布、U字型の分布まで表現できる便利な分布です⁵。カシオのとても便利なサイトがあるので、そこでベータ分布を計算してみると、

このように、βが1より小さければU字型の分布、1なら一様分布、1より大きければ山型の分布になります。

これをRICAPで置き換えて考えると、もしβが1e-7とか小さな値だったら、ベータ分布の値はほぼ0か1しか出ないので、RICAPを使っても元の画像と変わらないような画像が出てきます。つまり、βが小さな値だったらRICAPがほとんどないに等しいということができます。

逆にβが1なら、グラフで見たようにベータ分布は一様分布になるので、左上のパッチサイズは0～元画像のサイズ分の一様乱数で選ぶのと等しくなります。ありとあらゆるサイズのパッチができるため、元画像とは全然違う出力になります。つまり、β＝1のときはRICAPが強い作用があるということがわかります。

RICAPの直感的な効果は、「ニューラルネットワークの活性化するニューロンを変えながら訓練する」にあると思います。なぜなら、パッチの合成によって画像の位置が大きく変わるからです。つまり、同じ画像で位置を変えながら訓練することで、より多くのニューロンを訓練し汎化性能を高める、Data Augmentationのベーシックな手法の反転やランダムクロップと本質的には同じだと思います。

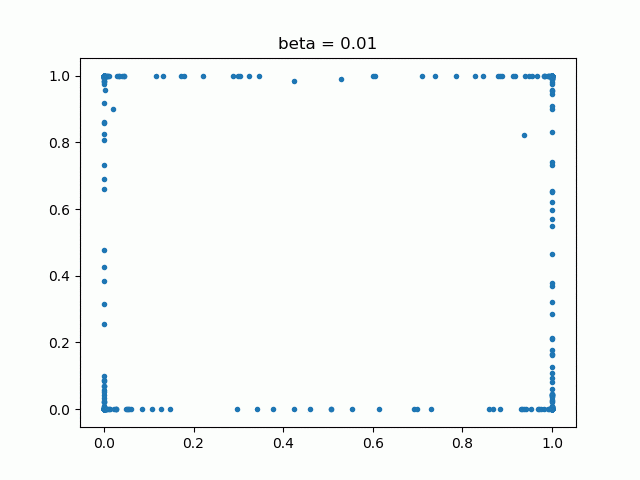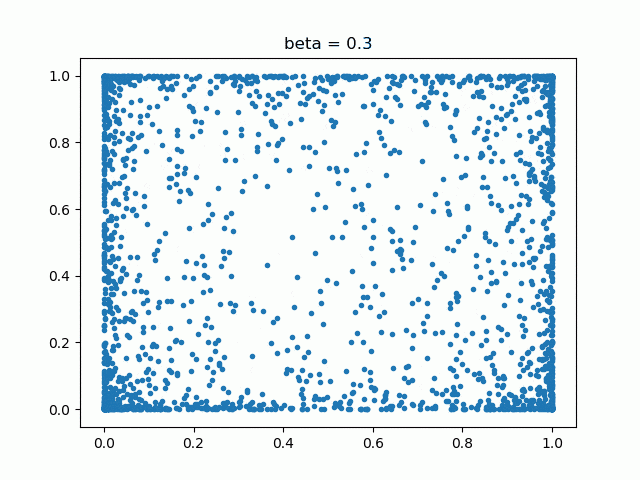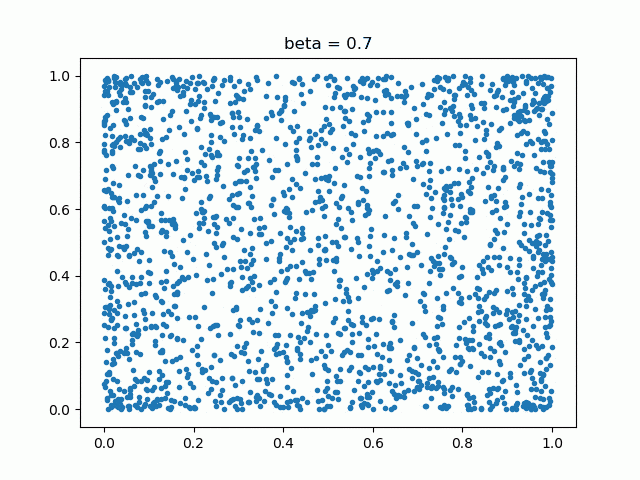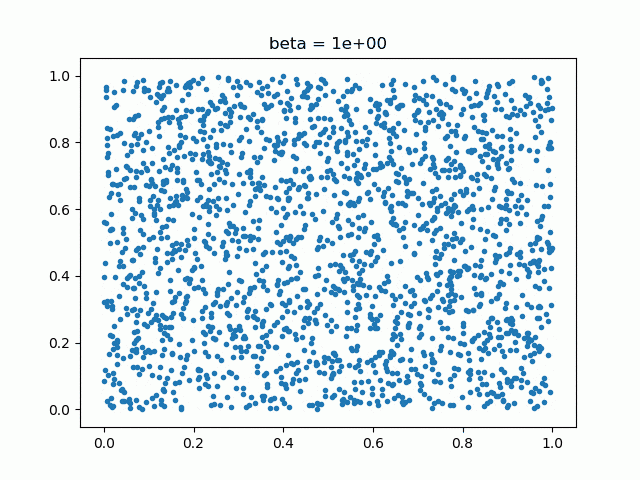
では、RICAPもとい、Data Augmentationが活性化するニューロンの位置を変えながら訓練するというのなら、RICAPのβとどのような関係があるでしょうか。2次元でベータ分布の乱数をプロットしてみました。

βが小さいと四辺に固まっていて、βが大きくなると中央に繰り出してくるというのがわかります。例えばβが小さいと（0.1や0.3）、中央に近い部分のニューロンはなかなか訓練されないのではないでしょうか。しかし、初めから高いβ（1.0）を使うと、訓練が思ったように進まなく精度が下がってしまうそうです。これらを総合して考えると、固定のβよりも「訓練中にβを変化させて、いろんなβで訓練させたほうが良いのではないか」という疑問がわきます。

今回は次の3点を見ていきます。

オリジナルの論文ではRICAPでバッチ単位で固定の乱数を使っているが、これをサンプル単位で別の乱数を使ったらどうか？
さらに訓練中にβの値を変化させたらどうか？
さらにそれを転移学習で使ったらどうか？

内容的には前の記事とかぶりますが、今回はCIFARを使ってもうちょっとちゃんと見ていきます。

バッチ単位で同一の乱数 vs サンプル別に違う乱数

オリジナルの論文では、RICAPで使うベータ分布の乱数をバッチ単位で使いまわしていました。例えば、ベータ分布の乱数を発生させて0.2が出てきたら、ミニバッチ内の全ての画像に対して0.2として計算しています（同一の乱数）。

ただこれだと偏った最適化が行われてしまうので、この使いまわしをやめて、サンプル単位で別々のベータ乱数を出すようにしてみます（異なる乱数）。異なる乱数の場合でもパラメーターβの値は同じですが、乱数なので出てくる値が変わります。

まず、ベースラインとしてRICAPを使わない（β＝0）の例（ベースライン）を確かめ、次に同一の乱数、異なる乱数について「β＝0.1、0.3、0.5、0.75、1」の計10ケース確かめました。全ケース1回のみ試しています。

転移学習は使わないVGGライクなネットワークで、Google ColabのTPUで訓練させ、学習率は0.01のAdam、バッチサイズは2048とし、150エポック訓練させました。時間の都合上高速化させたかったのでバッチサイズを大きくしました。

コードはこちらにあります。
RICAPコード：
https://github.com/koshian2/keras-ricap/blob/master/ricap.py
訓練コード：https://gist.github.com/koshian2/3a7f16c103cb29ceca0726a45b7d821f

以下は最大テスト精度の比較です。

β	同一乱数	異なる乱数
0（RICAPなし）	87.84%	-
0.1	87.56%	88.78%
0.3	88.60%	88.71%
0.5	88.29%	88.75%
0.75	88.37%	88.18%
1	88.18%	88.42%

まずはRICAPの有効性について。β＝0（RICAPなし）の場合は、87.84%だったのに対して、10ケース中9ケースで88%を越えているので、乱数が同一だろうが異なろうがRICAPは効いているということになります。

次に、乱数をバッチ単位で同一か、サンプル単位で違うものにしたほうがいいかということについて。かなり僅差ですが、βの値について5ケース中4ケースで異なる乱数にしたほうが良かったので、サンプル単位で乱数を発生させた（使い回さない）ほうが良いのではないかと思われます。

βを周期的に変化させる

次に、「いろんなβを同時に試したほうがよいのではないか」という点について試してみたいと思います。ここでは、コサインカーブを使ってβの値を周期的に変えてみます。

実はβの調整にコサインカーブを使うというのはクレイジーに聞こえますが、学習率の調整では既に論文があって「SGDR: Stochastic Gradient Descent with Warm Restarts」、こちらではコサインカーブで学習率を上げたり下げたりしています。三角関数ならこういう周期性のある変動得意ですからね。

式もSGDRの式をほぼ使いまわして、以下の式で変動させてみました。

$$\beta_t=\beta_{min}+\frac{1}{2}(\beta_{max}-\beta_{min})(1-\cos(\frac{t}{T_p}\pi)) $$

$t$は現在のエポック数、$\beta_{min}, \beta_{max}$はβの変動させる最小値、最大値を入れています。$\beta_{min}$は0.01で固定します。またSGDRの式から以下の点を変えています。

最初に低いβになるようにする。βを上げると訓練精度が下がるので、最初に大まかに訓練させるには低いβのほうがいい。そのためコサインの項は最初0になって、だんだん大きくなるように調整する。
扱いやすいように、周期$T_p$を固定にした。SGDRには周期を変えていくというのもあるが、今回は扱いやすいように周期を定数にした。もちろん、周期を変動させていくような設定もありだと思う⁶。

乱数は全てサンプル単位で異なる乱数を使うようにしました。その上で、周期$T_p$を「5,10,20,50,100」と変動させ、また$\beta_{max}$を「0.5、1」の計10ケースを試してみました。設定は先程と同じで、バッチサイズ2048、150エポック訓練させています。

コードはこちらにあります：https://gist.github.com/koshian2/aa697ceea8918303edfc0f21a9054c10

結果は以下のとおりです。

周期	βMAX=0.5	βMAX=1.0
5	88.87%	88.45%
10	89.59%	89.27%
20	89.33%	89.25%
50	89.55%	89.42%
100	88.79%	88.90%

参考：ベースライン　RICAPなし＝87.84%
β固定のRICAP最大　固定乱数の場合＝88.60%（β=0.3）、異なる乱数の場合＝88.78%（β＝0.1）

最も良かったのは、$\beta_{max}=0.5, T_p=10$で89.59%でした。コサインカーブでゆらすことで1%近く上がりました。βをコサインカーブで変動させると、かなりのケースでβ固定の場合で到達できなかった89%台に到達することができました。

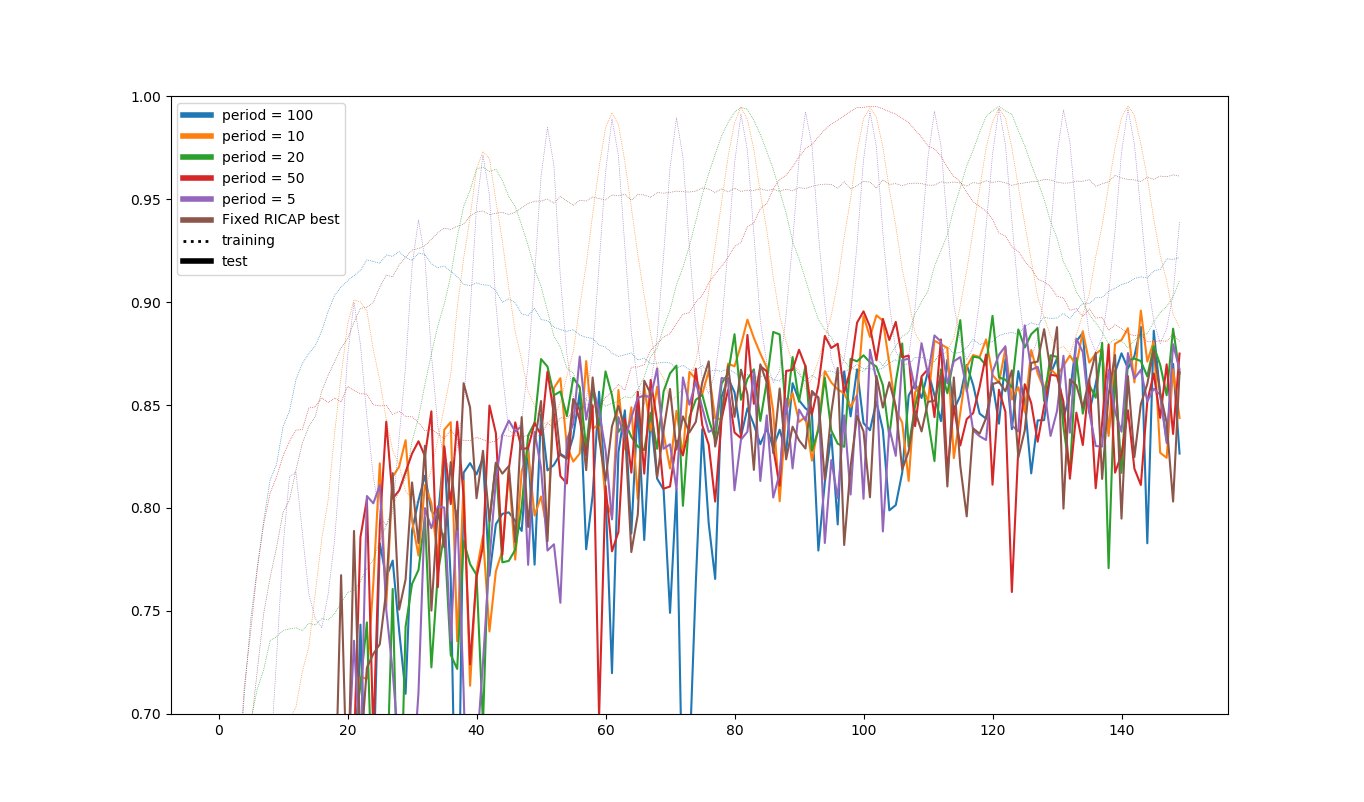
$\beta_{max}=0.5$の場合の、訓練・テスト精度をプロットすると次のようになります（固定の場合：異なる乱数でβ＝0.1の場合も最後に入れました）。かなり面白いプロットです。

これを見ると、訓練精度はβの変動とほぼ連動しているものの、テスト精度はあまり連動していないというのがわかります。また、訓練精度は最後ほぼ行ったり来たりしているだけですが、それでもまだテスト精度側の学習は進んでいるようです（テスト精度は周期性のある右肩上がりのグラフとなっています）。

また、テスト精度の振幅がコサインカーブを入れない場合より大きくなっており、「良い値を出すときは出すんだけど、ダメなときもかなりダメ」という形です。たまたまうまく行ったときのモデルを取りたいときはこれでもいいのではないかな、と思います。どうせコサインカーブ入れないときもある程度周期的な動きをするので。

転移学習でも確かめてみる

今まではまっさらなネットワークを訓練していましたが、今度は転移学習でやってみます。MobileNetを転移学習させます。

1から訓練させる場合とは条件を変えて学習率は1e-4のRMSPropに変え、バッチサイズは1024にしました。100エポック訓練させます。この条件だとData Augmentationを使わなくても93%ぐらいの精度は出ることは前に確認しています。

以下の6条件を調べました。

RICAPなし
RICAPあり、β＝0.3で固定
RICAPあり、β＝0.5で固定
RICAPあり、$\beta_{max}=0.5$で、$T_p=20$のコサインカーブでβを変動させる
RICAPあり、$\beta_{max}=0.5$で、$T_p=50$のコサインカーブでβを変動させる
RICAPあり、$\beta_{max}=0.5$で、$T_p=100$のコサインカーブでβを変動させる

RICAPを使う場合は全てで、サンプル別に異なる乱数を使っています。

コードはこちらにあります：https://gist.github.com/koshian2/f300153f475cd5ac3bb86ff19b919bba

結果は以下の通りです。

case	RICAP	コサインカーブ	βMAX(*1)	周期	テスト精度
1	☓	☓	0	-	93.37%
2	○	☓	0.3	-	95.25%
3	○	☓	0.5	-	95.06%
4	○	○	0.5	20	95.12%
5	○	○	0.5	50	95.04%
6	○	○	0.5	100	95.29%

RICAPを入れなくてもCIFAR-10で93.37%出ますが、RICAPを入れただけで95%台に乗ります。転移学習でもRICAPは明確に効きます。

そしてコサインカーブの影響ですが、これは結構際どくて、入れたほうが0.04%高くなりましたが、もしかしたら転移学習の場合は入れても入れなくても変わらないかもしれません。もしコサインカーブを入れるのだったら、fine-tuningでは大きめの周期を入れるといいかもしれません。

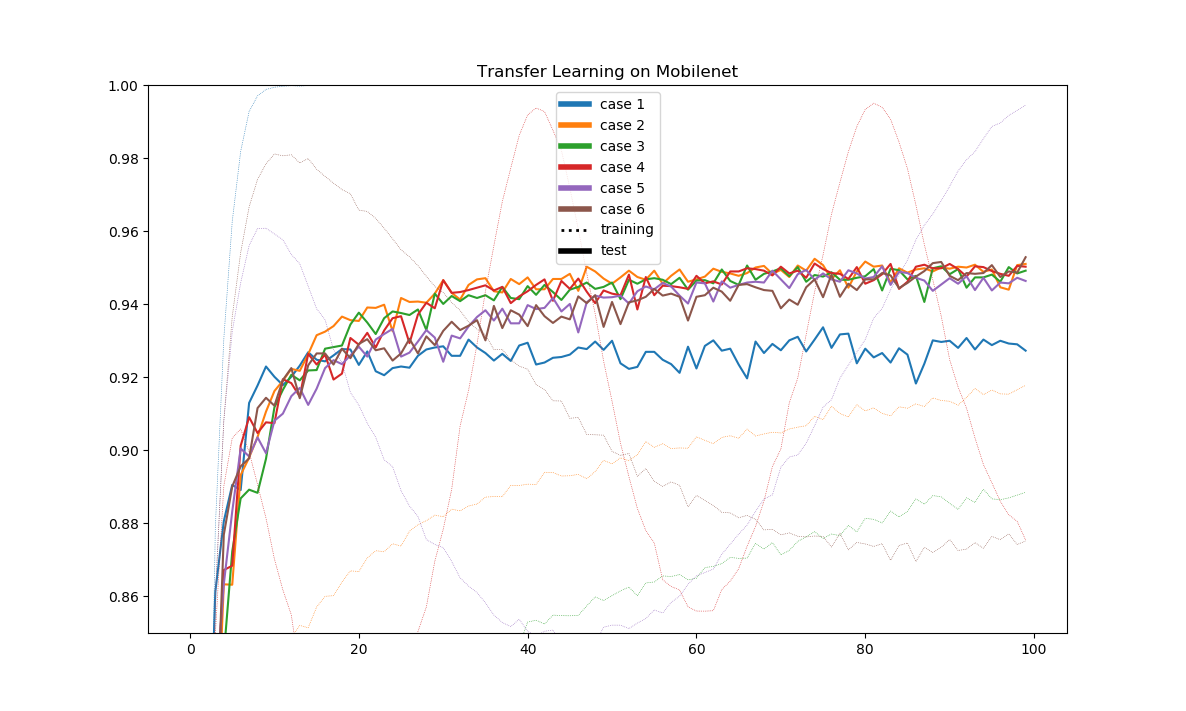
結果はこのとおり。case4～6がコサインカーブありです。最後にcase6がちょびっとまくっていますね。case4のように短い周期では固定のcase2とほぼ変わりませんが、case6のように長い周期ではゆっくりと学習が進んでいるのがわかります。

まとめ

CIFAR-10でVGGライクなモデルで確かめたところ以下のことがわかりました。1から訓練させる場合は、

バッチ間で同一の乱数よりも、サンプル単位で異なる乱数を使ったほうが若干良さそう
βをコサインカーブで変動させるとかなり良くなる

またMobileNetでの転移学習の場合は、

転移学習でもRICAPは効くのは確か
コサインカーブについては、効いているのかどうかよくわからなかったが、もし使うのなら長めの周期が良いのではないか

Data Augmentation using Random Image Cropping and Patching for Deep CNNs　https://arxiv.org/abs/1811.09030 ↩
クロップするサイズは完全ランダムではなく、ちゃんとした計算式はあります。詳しいことはこちらを参照ください　https://qiita.com/4Ui_iUrz1/items/e35e5f9210bbef693d05 ↩
実はこの手法は別に珍しくもなく、MixUPで既に提唱されていて、RICAPはMixUPを変えたものなのです。MixUPの論文を読むと、このようなラベルの合成はGANの安定化に寄与するそうです。Discriminatorで本物、偽物を0,1で訓練させるのではなく、多少混ぜたほうがいいよということだと思います。 ↩
データソース：　http://www.nurs.or.jp/~nagadomi/animeface-character-dataset/ ↩
例えばベイズ統計では、コイン投げで表が出る確率を推定するような問題で、事前分布にベータ分布を仮定します。すると事後分布もベータ分布となり、直接積分を計算することなくパラメーター間の計算でベイズ更新ができます。ベイズ統計ではベータ分布が大活躍します。　http://r-tips.hatenablog.com/entry/beta-distribution ↩
ちゃんと確かめていないので、多分ですが、周期を可変でやる場合は、周期は始め短くしてだんだん長い周期に変えていくのが成功すると思います。大まかに訓練してあとは細かいところを調整していけばいいので。 ↩