最近出たホットなData Augmentation、「RICAP(Data Augmentation using Random Image Cropping and Patching for Deep CNNs)」というのを使ってみました。以前やったアニメ顔のデータセットで試してみたいです1。以前の記事
RICAPを少しいじって、ベータ分布のパラメーターのスケジューリングもやってみました。
RICAPって何?
画像を4枚つなぎ合わせてデータの水増し(Data Augmentation)する手法。MixUpが2枚の画像を全体を組み合わせて足す手法なら、RICAPは4枚の画像をクリッピングして合成するというキメラのような手法。MixUPが効くならRICAPも効くのもなんとなく理解できます。
理論のほうは以下の記事で詳しく解説されているので、ぜひこちらを参考にしてください。自分も実装する際に相当参考にしました。
CIFAR-10でSOTAなエラー率2.19%を達成したdata augmentation手法 RICAP を試してみた
https://qiita.com/4Ui_iUrz1/items/e35e5f9210bbef693d05
この論文の著者は神戸大学の方で、日本人チームです。なかなか面白い手法ですね。
RICAPを確かめる
論文にはPython(PyTorch)のコードが載っていますが、KerasだとNumpyで操作できたほうが楽なのでNumpyベースに書き換えました。ちなみに、論文のコードはベータ分布の乱数が同一ミニバッチ間で共通の値を使っていますが、必ずしもそれが正しいとは自分は思いませんでした。ベータ分布の乱数がミニバッチ間で共通の値を使う例、ベータ分布の乱数をサンプル別に変える例の両方を書いてみました。
import numpy as np
def ricap(image_batch, label_batch, beta=0.3, use_same_random_value_on_batch=True):
# if use_same_random_value_on_batch = True : same as the original papaer
assert image_batch.shape[0] == label_batch.shape[0]
assert image_batch.ndim == 4
batch_size, image_y, image_x = image_batch.shape[:3]
# crop_size w, h from beta distribution
if use_same_random_value_on_batch:
w_dash = np.random.beta(beta, beta) * np.ones(batch_size)
h_dash = np.random.beta(beta, beta) * np.ones(batch_size)
else:
w_dash = np.random.beta(beta, beta, size=(batch_size))
h_dash = np.random.beta(beta, beta, size=(batch_size))
w = np.round(w_dash * image_x).astype(np.int32)
h = np.round(h_dash * image_y).astype(np.int32)
# outputs
output_images = np.zeros(image_batch.shape)
output_labels = np.zeros(label_batch.shape)
def create_masks(start_xs, start_ys, end_xs, end_ys):
mask_x = np.logical_and(np.arange(image_x).reshape(1,1,-1,1) >= start_xs.reshape(-1,1,1,1),
np.arange(image_x).reshape(1,1,-1,1) < end_xs.reshape(-1,1,1,1))
mask_y = np.logical_and(np.arange(image_y).reshape(1,-1,1,1) >= start_ys.reshape(-1,1,1,1),
np.arange(image_y).reshape(1,-1,1,1) < end_ys.reshape(-1,1,1,1))
mask = np.logical_and(mask_y, mask_x)
mask = np.logical_and(mask, np.repeat(True, image_batch.shape[3]).reshape(1,1,1,-1))
return mask
def crop_concatenate(wk, hk, start_x, start_y, end_x, end_y):
nonlocal output_images, output_labels
xk = (np.random.rand(batch_size) * (image_x-wk)).astype(np.int32)
yk = (np.random.rand(batch_size) * (image_y-hk)).astype(np.int32)
target_indices = np.arange(batch_size)
np.random.shuffle(target_indices)
weights = wk * hk / image_x / image_y
dest_mask = create_masks(start_x, start_y, end_x, end_y)
target_mask = create_masks(xk, yk, xk+wk, yk+hk)
output_images[dest_mask] = image_batch[target_indices][target_mask]
output_labels += weights.reshape(-1, 1) * label_batch[target_indices]
# left-top crop
crop_concatenate(w, h,
np.repeat(0, batch_size), np.repeat(0, batch_size),
w, h)
# right-top crop
crop_concatenate(image_x-w, h,
w, np.repeat(0, batch_size),
np.repeat(image_x, batch_size), h)
# left-bottom crop
crop_concatenate(w, image_y-h,
np.repeat(0, batch_size), h,
w, np.repeat(image_y, batch_size))
# right-bottom crop
crop_concatenate(image_x-w, image_y-h,
w, h, np.repeat(image_x, batch_size),
np.repeat(image_y, batch_size))
return output_images, output_labels
「use_same_random_value_on_batch=True」とすれば論文と同じように「ミニバッチ間で共通の乱数を使う例」となります。。また、この値をFalseにすれば、「サンプル間で別々の乱数を使う例」となります。
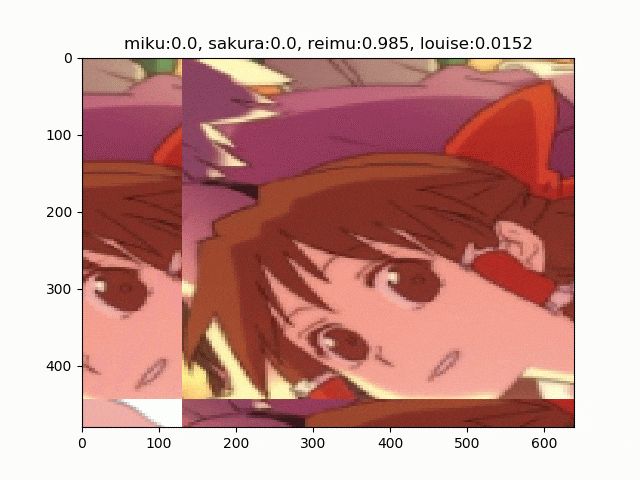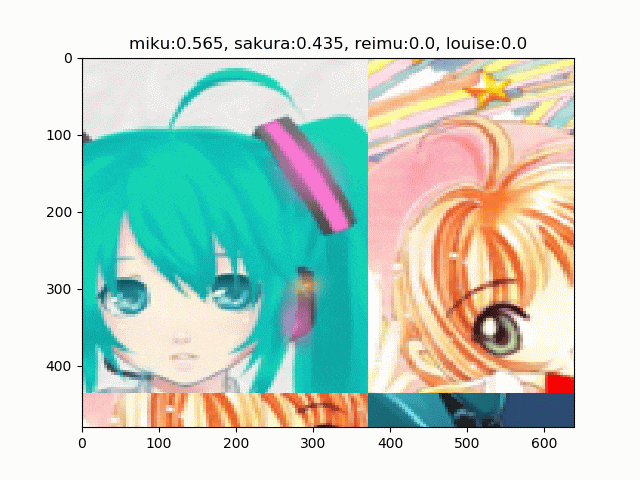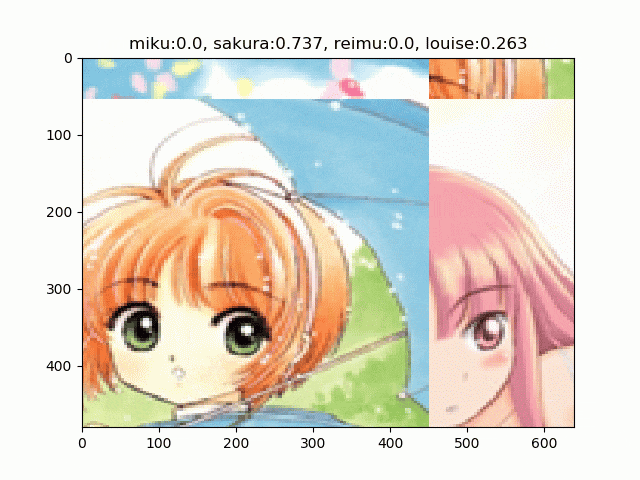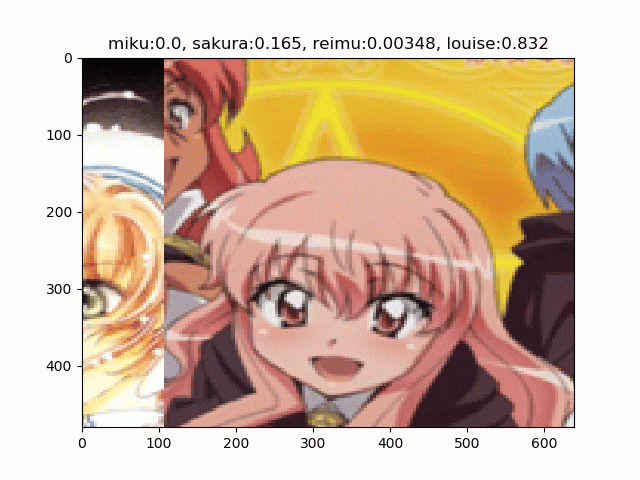
animeface-character-datasetから、「初音ミク」「木之本さくら」「博麗霊夢」「ルイズ」の4人のキャラクターの画像をimagesのフォルダーにコピーしました。これをRICAPでDataAugmentationしてみます。
これをImageDataGeneratorに食わせてループさせます。実際に使うときはImageDataGeneratorを継承して使うと簡単だと思います。
from keras.preprocessing.image import ImageDataGenerator
from ricap import ricap
import numpy as np
import matplotlib.pyplot as plt
def example():
batch_size = 8
generator = ImageDataGenerator(rescale=1.0/255)
charas = ["miku", "sakura", "reimu", "louise"]
for batch_X, batch_y in generator.flow_from_directory(
"images", target_size=(480,640), batch_size=batch_size):
ricap_X, ricap_y = ricap(batch_X, batch_y, 0.5, False)
for i in range(batch_size):
plt.imshow(ricap_X[i])
probs_str = [charas[j]+":"+f"{ricap_y[i][j]:.03}" for j in range(4)]
plt.title(", ".join(probs_str))
plt.show()
if __name__ == "__main__":
example()
これをバッチ間で同一の乱数を使う例、サンプルごとに別の乱数を使う例で見てみます。β=0.5としました。
バッチ間で同一の乱数を使う例
これは論文と同じ例です。このように画像がタイルされて表示されるのがRICAPの特徴です。バッチサイズの8サンプルごとに、タイルの結合位置が変わっているのがわかります。
サンプル別に異なる乱数を使う例
自分はこっちのほうが自然かなと思ったのですが、ベータ分布の乱数をサンプル単位で発生させて、結合位置をサンプル単位で変えてみました。論文ざっと探していたところこれについての検討はなかった(あったら自分の読み方が適当なだけでしかないので大変申し訳無い)ので、これも検討してみます。
なぜこっちのほうが自然かと思った点ですが、例えばMixUPをネットワーク内でやるような発想のShake Shakeでは、バッチ単位でShakeするのと、サンプル単位でShakeするのと両方検討していて、それによるとサンプル単位でShakeしたほうが結果が良かったそうです。それに、乱数を使っているのにバッチ内で共通の値を使って偏った訓練をするというのは、特定の箇所のニューロンが育ちやすいのか、それとも偏りを起こしやすいのかちょっとよくわからないですよね。
アニメ顔の分類
以前と同じようにDenseNetの転移学習をしました。しかし、オプティマイザーをRMSProp+学習率を1e-4にしたり、バッチサイズをTPUにあわせて1024にしたり若干変わっています。
詳しいコードはこちら:https://github.com/koshian2/keras-ricap/blob/master/train.py
以下の条件で行いました。
- ベースライン:上下左右15pxのシフトを行い、左右反転を行う
- ベースライン+β=0.1のRICAP
- ベースライン+β=0.3のRICAP
- ベースライン+β=0.5のRICAP
なお、RICAPは共通の乱数を使う場合、異なる乱数を使う場合の両方を試しています。
同一の乱数の場合の結果
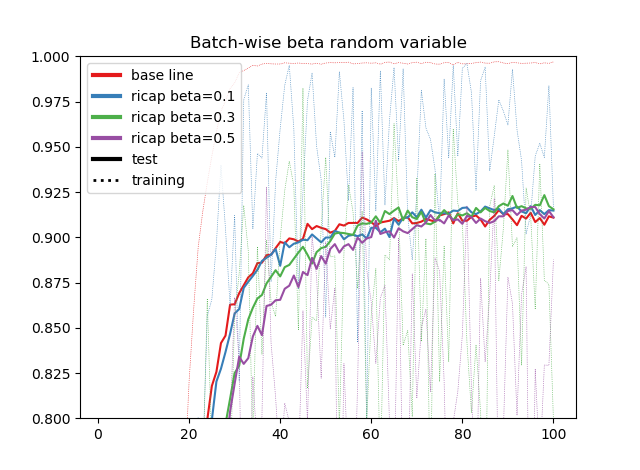
本来の論文の手法です。**ベースラインのテスト精度が91.5%だったのに対して、RICAPのβ=0.3が最も高く92.3%**となりました。確かに効いているみたいです。
| 条件 | テスト精度 |
|---|---|
| ベースライン | 91.5039% |
| 同一の乱数のRICAP β=0.1 | 91.7236% |
| 同一の乱数のRICAP β=0.3 | 92.3340% |
| 同一の乱数のRICAP β=0.5 | 91.6748% |
テスト精度はよくても訓練精度がガタガタで、これは同一の乱数を使っているせいでかなり局所的な最適化が行われたのではないかと思われます。偏った最適化をして最大瞬間風速みたいなテスト精度が取れたような感は否めません。ただ精度はきっちり出ているので効果は認めるべきでしょう。
そしてβが大きくなると、訓練精度よりもテスト精度のほうが高くなるという変わった現象がおきます。これは異なる乱数を使ったときのほうがわかりやすく出るのですが、半教師あり学習の疑似ラベル(Pseudo Label)のときに見たような挙動です。確かに訓練画像のほうはRICAPで未ラベルデータに似て非なるなにか(上手いことばが出てこない)を載せているので、なんとなく理解できます。
ただ、Pseudo Labelのときは転移学習ではうまく行かなかったのですが、RICAPは転移学習でもうまく行きます。そこは大きな違いであり、メリットだと思います。
異なる乱数の場合結果
次に自分が勝手に思いついた「サンプル間で異なる乱数を使う」という方法です。
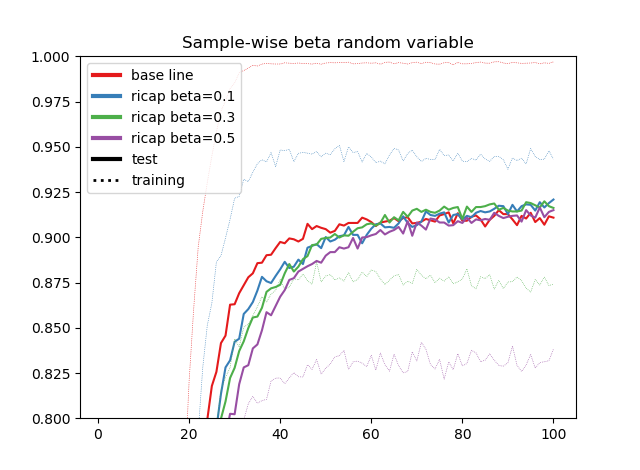
効きとしては同一の乱数を使うよりも弱くなりましたが、その分訓練誤差の暴れ方が少なくなりました。つまり、同一の乱数のときよりも偏った最適化をしなくなったということですね。
| 条件 | テスト精度 |
|---|---|
| ベースライン | 91.5039% |
| 異なる乱数のRICAP β=0.1 | 92.0898% |
| 異なる乱数のRICAP β=0.3 | 91.9922% |
| 異なる乱数のRICAP β=0.5 | 91.6504% |
おそらく最大瞬間風速で精度を出したいのなら論文の通り同一の乱数を使うべきでしょうが、結果的にはこちらのほうが解釈しやすいです。なぜなら、βの大きさそのものがイメージ的には「正則化の強さ」と考えることができるからです。
確かに訓練精度は、ベースライン>β=0.1>β=0.3>…とβが大きくなるにつれて下がっていますし、テスト精度の上がるスピード(最終的な値の良し悪しとは異なります)もβの大きさと比例しています。疑似ラベルのときにあった「Entropy Regularization」とのアナロジーで見ると面白いかもしれませんね。
βのスケジューリング
さて、半教師あり学習と似てるよねということは、疑似ラベルで見たようなスケジューリングができないでしょうか? 具体的にはRICAPのβを訓練開始時には低い値にして、だんだん増やしていくという方法です。疑似ラベルでの$\alpha(t)$みたいな関数を作ります。
ここでは$t$をエポックの変数として、RICAPのβを以下のような$\beta(t)$という関数で定義してみました。
\beta(t) = \begin{cases}
\beta_{min} \qquad t<T_1 \\
\frac{t-T_1}{T_2-T_1}(\beta_{max}-\beta_{min})+\beta_{min} \qquad T_1 \leq t<T_2 \\
\beta_{max} \qquad T_2\leq t
\end{cases}
ここでは、ベータ分布のβに0をおけないためにちょっとややこしい式になっていますが、$\beta_{min}=0.01, \beta_{max}=1$としました。つまり、最初の方はほぼRICAPなしで訓練しているものの、だんだんRICAPの強さを増やしていって最後は一様分布で訓練させます。RICAPは非常にユニークな方法ですが、論文よりももっと変態的な改造はできます。
ここでは100エポック訓練させるものとして、$T_1=20, T_2=90$としました。つまり、20エポック目から70エポックかけてゆっくりβの値を上げていきます。具体的な実装としては、GeneratorとCallbackをくっつければ特に問題ないです。
コードはこちらにあります:https://github.com/koshian2/keras-ricap/blob/master/train_on_schedule.py
結果
乱数をバッチ間で同じ値を使う例(オリジナル)、サンプルごとに別々の値を使う例の両方でやってみました。
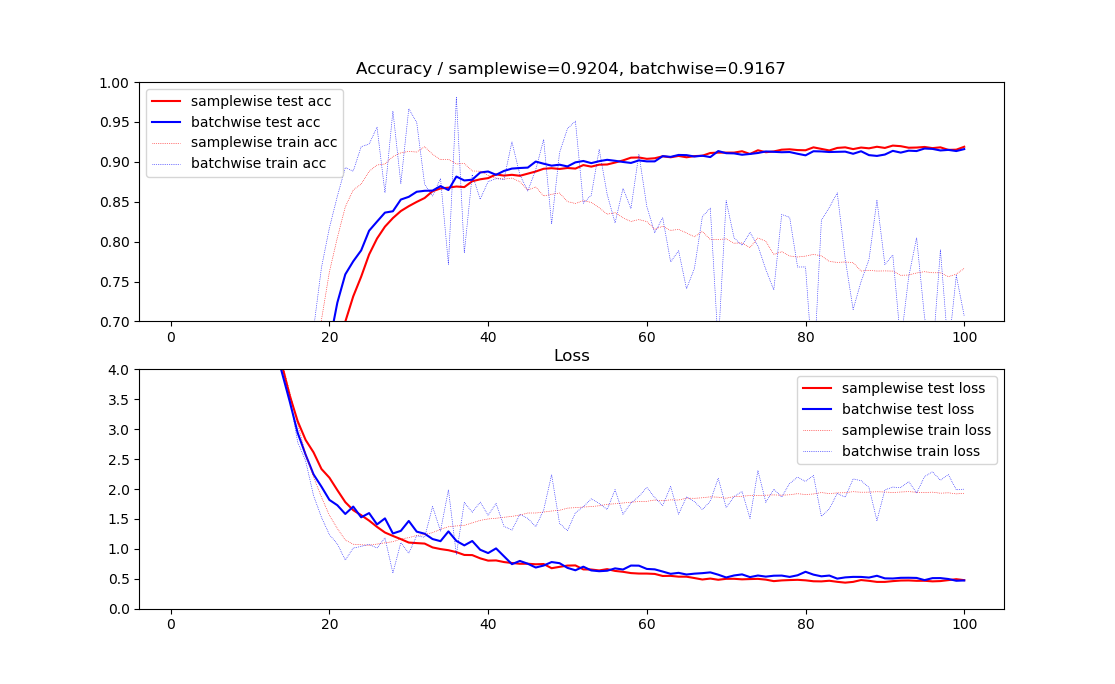
差は僅差ですが、このようにスケジューリングする場合は、サンプルごとに別々な乱数を使うほうがどうもうまくいくようです。このグラフの直感的な解釈はわかりやすくて、はじめは訓練精度や訓練誤差のほうが良いです。しかし、βの値を上げていくとテスト精度はゆるやかに伸び続けるものの、訓練精度はだんだんと下がっていき、そのうち訓練とテストの精度が逆転するということがおきます。多分こんな感じになるだろうと思っていました。
なぜ訓練精度が下がってもテスト精度が上がり続けるのかというと、半教師あり学習でのEntropy Regularizationと似たような正則化が機能しているのではないかと思います。これがEntropy Regularizationがどうかはよくわかりません。
そしてこのグラフの傾向から見れば、別々の乱数のほうがゆるやかに変動しているので、具体的に精度が出る出ないは別として、別々の乱数を使ったほうがどうもスケジューリングという観点ではそぐうのかなと思います。
そしてスケジューリングの意味ですが、ベータ分布というのはβが1未満ならグラフの0と1に近い部分、1以上なら0.5を中心にとムラが出やすいので、このようにまんべんなくスケジューリングでずらしていったほうがおそらく全体のニューロンが訓練されやすいのではないかなと思います。ここはちゃんと検証していないので、もしかしたらただの思いこみなのかもしれません。
まとめ
- RICAPというData AugmentationをKerasで使うことができた
- 乱数をサンプル間で別々の値を使うか、バッチ間で別々の値を使うか、ベータのスケジューリングをするか、まだまだ改良の余地はありそう
- 半教師あり学習の視点から見ていくと「精度が出た、出ない」以上の理論的なアプローチからの議論ができるのではないか、という感想
リポジトリはこちらにあります。RICAPだけにGitHubにもちゃんとコミットしました。
https://github.com/koshian2/keras-ricap
参考文献
Ryo Takahashi, Takashi Matsubara, Kuniaki Uehara. Data Augmentation using Random Image Cropping and Patching for Deep CNNs. ACML2018. 2018