CVPR2021 Best Paperの『GIRAFFE』を徹底解説！ オブジェクト単位で変形でき、静止画から教師なしでDisentangleできる3Dレンダリングベースの生成モデルとは？

2021年のディープラーニング論文を1人で読むAdvent Calendar23日目の記事です。今日読むのは「CVPR2021 Best Paper」に選ばれたGIRAFFEという論文です。著者はドイツのマックスプランクインテリジェントシステム研究所とテュービンゲン大学の方です。

この論文は分類としては生成モデル（GAN）なのですが、NeRF（Neural Radiance Fields）の系列を汲んでいて、従来のGANとは全く異なったアプローチをとります。GANが初めてという方だとかなり読むのが厳しい内容です。逆に3Dレンダリングの技術（特にボリュームレンダリング）をフル活用しているので、3Dに詳しい方なら逆にわかりやすいかもしれません。

自分はボリュームレンダリングを知ったのがこれが初めてで、NeRFの系列も読んだのが初だったのですが、「5次元のパラメーターによるカメラのコントロール」「ボリュームレンダリング」を知ったら理解できました。その前提知識も含めて丁寧に解説していきます。この論文はコードを読むより、論文を読むのが一番わかりやすいです。プロジェクトページに生成結果が多くあるので、それを先に見るとアウトラインがつかめます。

• タイトル：GIRAFFE: Representing Scenes As Compositional Generative Neural Feature Fields
• URL：https://openaccess.thecvf.com/content/CVPR2021/html/Niemeyer_GIRAFFE_Representing_Scenes_As_Compositional_Generative_Neural_Feature_Fields_CVPR_2021_paper.html
• 出典：Michael Niemeyer, Andreas Geiger; Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021, pp. 11453-11464
• コード：https://github.com/autonomousvision/giraffe
• プロジェクトページ：https://m-niemeyer.github.io/project-pages/giraffe/index.html

指定位置にあるから2D画像をレンダリングしたい

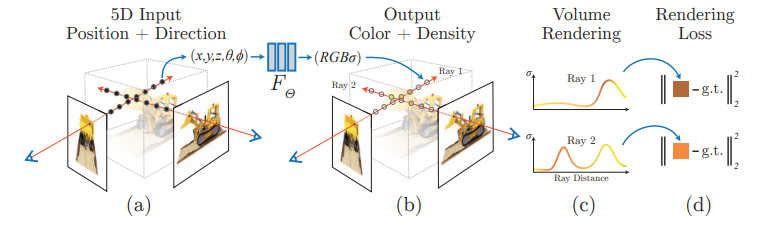
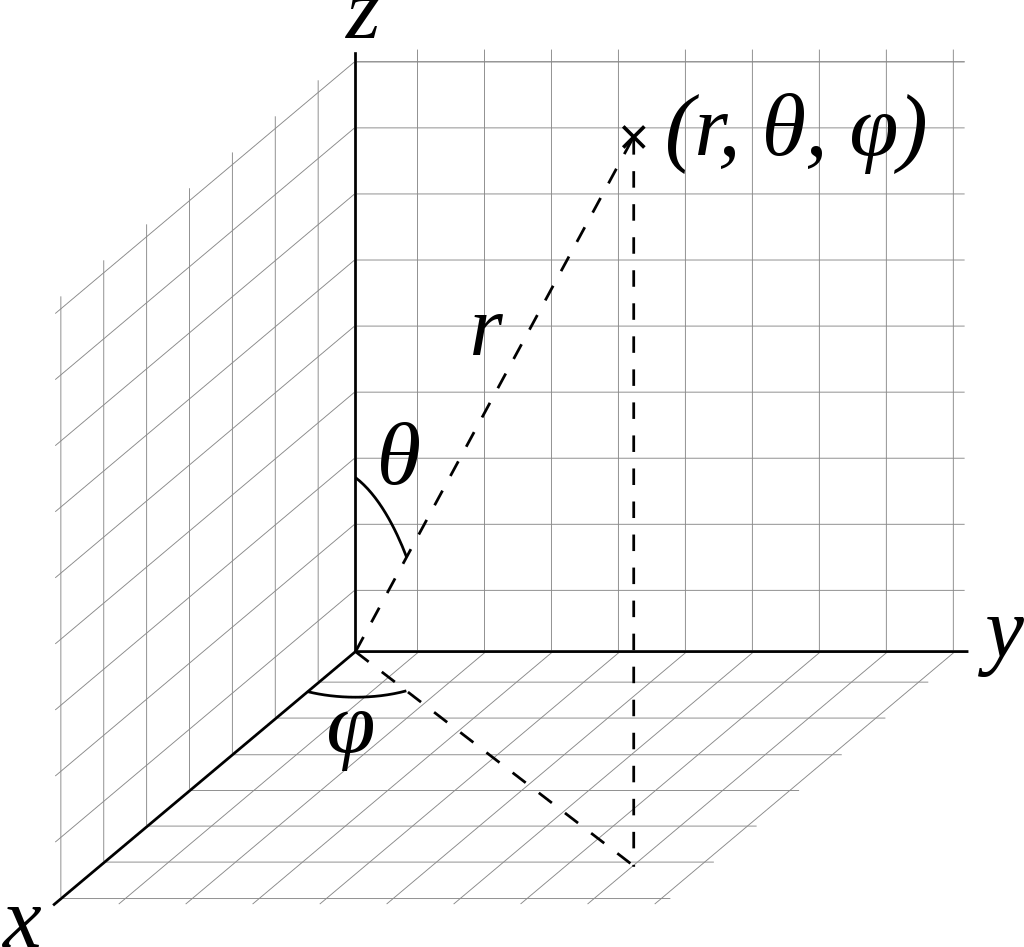
この論文（GIRAFFE）を理解するには、まずNeRFにはじまるNeural Radiance Fieldsのお気持ちを理解しておかないといけません。やりたいことは3次元空間で特定の位置にカメラをおいて、カメラから見た2D画像をレンダリングすることです。CGの世界を想像してみてください。この図はNeRFの論文からの引用ですが、

(a)のような状況です。今いるのは3次元空間です。(a)では2本の矢印が出ていますが、左側に向かって進んでいる矢印に注目しましょう。矢印上にはいくつかの点がありますが、進む方向と逆の矢印の先にカメラがあると思ってください（図では$(x, y, z, \theta, \phi)$と書かれているところです）。このカメラがあったときの、2D投射画像を算出したいのです。

ではどう投射画像を計算したいのかということですが、線の上にある3次元の点のもっている情報を、集約計算していくというのが基本的な発想になります。

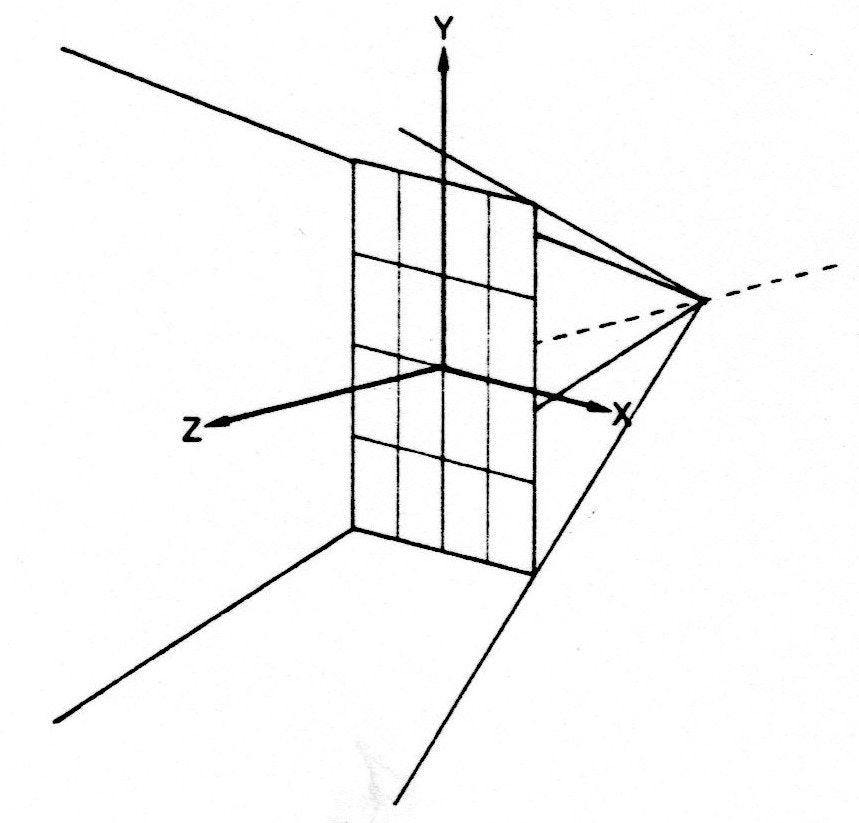
これは英語版WikipediaのRay Castingのページからのものですが、

奥から手前に向かっていくつかの線が出ていますよね。一番奥の線の交わっているところにカメラがあります。「なぜ線をいっぱい出しているのか」という点ですが、4隅の線同士を結んで、平面で囲めばそこがスクリーンとなるからです。手前のx, y, zと書いてある平面がスクリーンです。

このスクリーンをカメラからの距離に応じて作っていき、そのスクリーンを集約していけば目的の投射画像ができるというのが基本的な発想です。図では4本しか線が引いていませんが、スクリーン上のグリッドに応じていくつも線を引くことになります。この線はカメラからの光線とみなせるので、CGの世界では**レイ（Ray）**と呼ばれます。

今述べた手法は**レイキャスティング（Ray Casting）**というCGで広く使われている手法です。これをニューラルネットワークベースに落とし込んだのが、NeRFやGIRAFFEというわけです。集約計算は後で見ていくとして、次は「カメラのパラメーターがなぜ5次元なのか」をみていきましょう。

カメラのパラメーターが5次元である理由

NeRFの図ではカメラのパラメーターを$(x, y, z, \theta, \phi)$という5次元で表していました。なぜ5次元なのでしょうか？　GIRAFFEの論文ではここがいきなりポンと与えられているので、これを理解できないと開幕つまずくことになります。この理由を考えてみました。

$(x, y, z)$というのは3次元内の座標を表すので特に問題ないでしょう。これはカメラの位置そのものを表しています。

問題は$\theta, \phi$です。これは角度を表していますが、なぜ角度が2つでいいのでしょうか。x, y, zという3つの軸があるのだから、xy-yz-zxのように回転角が3つ必要ではないでしょうか。

大砲の気持ちになるのです

すごく唐突ですが、3Dの世界で大砲を打ち出すゲームを想像してください。

今この大砲は固定だとします。弾を任意の方向に打ち出すためには、どうコントロールすればよいでしょうか？

固定の大砲を、「上下左右」にコントロールできれば任意の方向に発射できることになります。実際の大砲は動かないので、大砲の向きを変えているつまり、大砲を垂直方向・水平方向に回転しているだけなのです。

位置が固定のとき、大砲を打ち出す方向は、大砲から見たら$\theta, \phi$という水平・垂直回転角が与えられれば一意に決まるということを示しています。だから回転角が2つでいいのです。

大砲＝カメラとみれば、固定のカメラから任意の方向へレイを出したいときは、回転角を2つ与えればレイを定義できるということを意味します。

極座標として考える

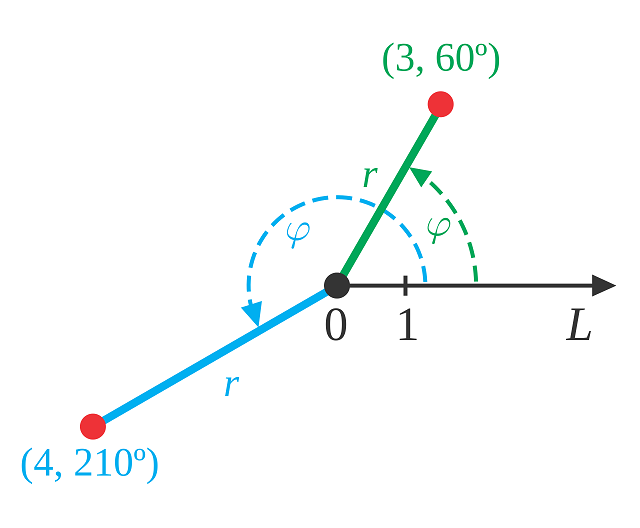
もう少し数学的な概念を使って説明すると、極座標として考えるのがわかりやすいです。平面の極座標では平面上の点は、$(r, \theta)$（図では$\phi$ですが）という、半径・回転角の2つのパラメーターで表記されます（図はWikipediaのPolar coordinate systemからです）。

$(r, \theta)$という2つのパラメーターが必要なのは点を表現する場合で、原点から出る任意の直線を表現したい場合は、パラメーターが1個落ちて回転角だけでいいです。なぜなら、この直線は「回転角が同一で半径が異なる点の集合」だからです。パラメーターが1個落ちるというのが重要です。

では3Dの極座標はどうでしょうか。3Dの極座標は、$(r, \theta, \phi)$という半径＋回転角2つで表現できます。

2Dと同様、あくまでこれは点を決める場合なので、線を決めたい場合は半径を落としてOKです。つまり、2つの回転角$\theta, \phi$で、3D空間で原点を通る直線は表現できるということになります。

カメラの定義に戻ると

GIRAFFEの論文では、3D空間上でのカメラのパラメーターを、座標$\mathbf{x}\in\mathbb{R}^3$、見る方向$\mathbf{d}\in\mathbb{S}^2$の5次元で管理しています。なぜ5次元なのかもう理解できましたね。

特に記述はありませんでしたが、$\mathbb{S}$は球の「Sphere」を意味しているものだと考えられます。回転角であるから値域の観点から実数全体とは異なるよというでしょうか。コードを見たら複素数のように扱いが異なる値ではありませんでした。

論文ではいきなり「座標は3次元、方向は2次元」と書いているので、ここの背景を理解しないまま読み進めるとなにがなんだかわからなくなってしまうと思われます。

ボリュームレンダリング

この論文を読む上で、3Dグラフィックのボリュームレンダリングを知っておくと理解しやすいです。

先程「レイ上の点を集約計算することで、カメラから見た投射画像が求められるよ」と述べましたが、集約計算をどうするのかかこの部分です。

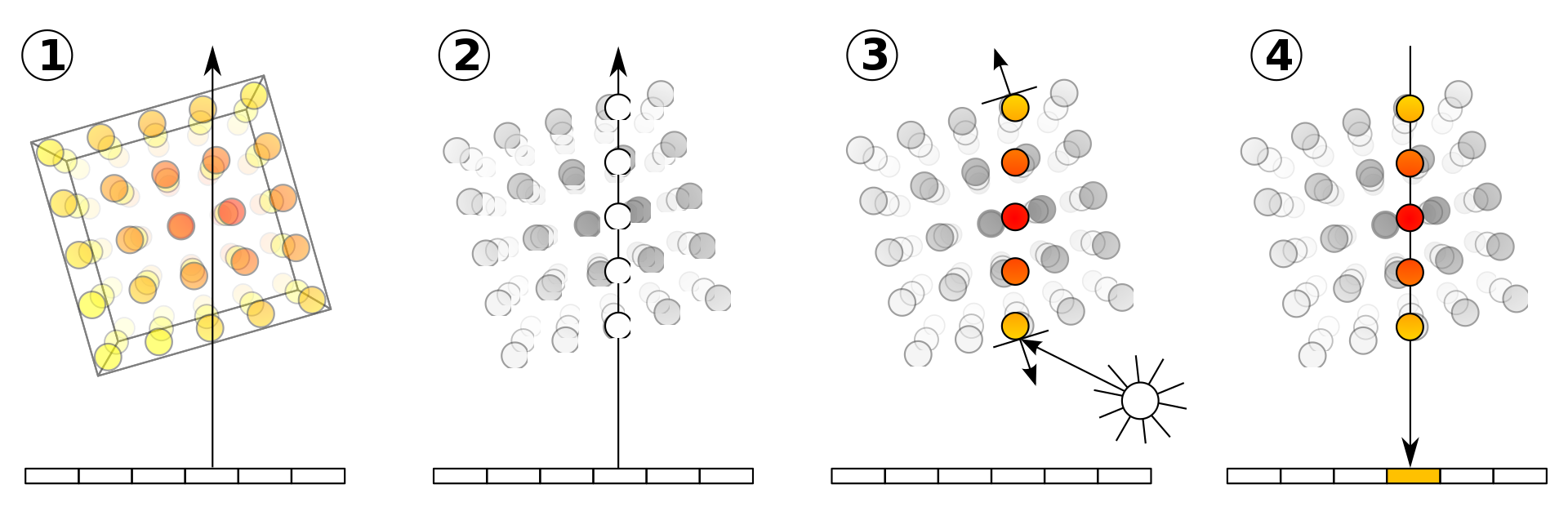
Wikipediaのボリュームレンダリングのページからの図ですが、これはレイに対して真上から見下ろすように捉えた図です。

図では物体上の各ピクセルのように表記されている点ですが、3D上では体積を伴った箱（ボクセル）として管理されています。今レイに対して集約計算するので、このように上から見てピクセルのように扱うことができます。

各ボクセルはRGB値と、不透明度を持っています。基本的にはレイに沿ってRGB値と不透明度を掛けるという方針ですが、カメラから見て手前のあるボクセルなのか、奥にあるボクセルなのかで不透明度の扱いが異なる（光の減衰を考慮する）ため、もう少し難しい計算をします。

今図の(2)のように、レイ上にボクセル値がサンプリングできたものとしましょう。ここから描画画像のRGB値は次の積分で計算されます。

$$I=\int_0^D c(x(\lambda))e^{-\int_0^\lambda \alpha(x(\lambda'))d\lambda'}d\lambda \tag{1}$$

$\lambda :0\to D$はレイ上のパラメーターです。$c(\cdot)$はレイ上のボクセルのRGB値、$\alpha(\cdot)$は同様に不透明度です。

指数関数の中での微分は$\lambda'$という別のパラメーターになっています。この積分は直感的には、「RGB値を不透明度で減衰させているが、遠くにあるボクセルほど不透明度の累積が積もっていって減衰され、寄与が小さくなる」ということでしょうか。式(1)は連続関数での話なので、実際は和や積を使った離散の表現をします。この式(1)を知っておくと、この論文の見通しが利きやすくなります。

ボリュームレンダリングの原理についてはこちらのページがわかりやすいので参照してください。この記事もこの記事を参考にしています。

https://www.ikeda-shoponline.com/ctsoft/technical_information/volume_visual/

Neural Features Fieldとしてのオブジェクト

「カメラのパラメーター管理」「ボリュームレンダリングの原理」という2つの道具が導入できたので、いよいよGIRAFFEの論文の内容を読解していきます。GIRAFFEの内容相当難しいのですが、論文がとにかくわかりやすく書かれているので、論文を読むのが一番わかりやすいです。初手コードだと多分なにやってるんだかわからなくなります。

Positional Encoding

カメラのパラメーターを、座標$\mathbf{x}\in\mathbb{R}^3$、見る方向$\mathbf{d}\in\mathbb{S}^2$が与えられます。これをVolume density（体積密度）$\mathbf{\sigma}\in\mathbb{R}^+$と、RGB値$\mathbf{c}\in\mathbb{R}^3$にマッピングしたいのです。

「Volume densityとはなんぞや？」と思いますが、直感的にはボクセルの不透明度に相当します。ただ、体積密度の空間は厳密にはボクセルと異なるので、GIRAFFEの論文ではボクセルとは呼んでいません。「ボクセルの不透明度に近いもので、RGB値と合わせてボリュームレンダリングで積分計算したいんだな」と思っておくと見通しが利きやすくなります。

最初にPositional Encodingのための関数を導入します。

$$\gamma(t, L) = (\sin(2^0t\pi), \cos(2^0t\pi), \cdots, \sin(2^Lt\pi), \cos(2^Lt\pi))\tag{2}$$

これはカメラのパラメーターをPositional Encodingするための関数です。Transformerで使われるPositional Encodingと結構近いですね。これを導入する意義は、回転角に対してより正準な姿勢を捉えることが可能になるからです（性能を上げるための手法です）。

実際に、Positional Encodingあり/なしで比較したのが以下の図で、

(a)がPositional Encodingあり、(b)がPositional Encodingを使わずに別の手法であるRandom Fourier Featuresを使った方法です。回転角を固定したときに、(b)は椅子の種類によって出力される角度がずれてしまっています。

Neural Radiance Fields

「Radiance Fields」とは直訳すれば輝度場ですが、NeRFの論文とも共通する内容です。カメラのパラメーターはを輝度場のパラメーター$(\sigma, c)$にマッピングしたいのです。このマッピングの関数を$f$とすると、

$$f_\theta: \mathbb{R}^{L_x}\times \mathbb{R}^{L_d} \to \mathbb{R}^{+}\times\mathbb{R}^3 \ (\gamma(\mathbf{x}), \gamma(\mathbf{d})) \to (\mathbf{\sigma}, \mathbf{c})\tag{3}$$

これはカメラのパラメーターから輝度場へのマッピングです。$f_\theta$は多層パーセプトロン（MLP）を使います。$\gamma(\cdot)$は式(2)のPositional Encodingの関数で、関数適用後の要素数が$L_x, L_d$です。Volume densityである$\sigma$の要素数が$\mathbb{R}^+$と謎の値ですが、「正の適当な要素数」という意味です。

Generative Neural Feature Fields

式(3)のNeRFには生成モデルの性質がありませんでしたが、これにGANのような生成モデルの性質を加えます。典型的なGANは$z\to I$のように、乱数から画像を直接生成しましたが、GIRAFFEの場合は輝度場（Neural Radiance Fields）を生成します。実装上は単純で、乱数を引数に加えます。ここで$\mathbf{z}_s$はオブジェクトの形を、$\mathbf{z}_a$は外観を表す乱数です。

$$g_\theta: \mathbb{R}^{L_x}\times \mathbb{R}^{L_d}\times \mathbb{R}^{M_s}\times \mathbb{R}^{M_a} \to \mathbb{R}^{+}\times\mathbb{R}^3 \ (\gamma(\mathbf{x}), \gamma(\mathbf{d}), \mathbf{z}_s, \mathbf{z}_a) \to (\mathbf{\sigma}, \mathbf{c})\tag{4}$$

これはGRAFという、先行研究のモデリングです。GRAFではRGB値を直接出力していましたが、本論文（GIRAFFE）では出力にワンクッションおいて$M_f$という特徴量の次元へとマッピングします。

$$h_\theta: \mathbb{R}^{L_x}\times \mathbb{R}^{L_d}\times \mathbb{R}^{M_s}\times \mathbb{R}^{M_a} \to \mathbb{R}^{+}\times\mathbb{R}^{M_f} \ (\gamma(\mathbf{x}), \gamma(\mathbf{d}), \mathbf{z}_s, \mathbf{z}_a) \to (\mathbf{\sigma}, \mathbf{f})\tag{5}$$

最終的なRGB値へのマッピングは、「Neural Rendering」という別のモジュールを使います。最初これは微分可能なレンダリングモジュールかなと身構えてしまいましたが、ただのConv2D中心のニューラルネットワークだったので安心しました。

$h_\theta$が本論文の提案手法で、この関数がこれからよく登場してきます。

オブジェクトの表現

この論文ではオブジェクト単位で移動可能な生成モデルを売りにしているので、オブジェクトの表現を定義する必要があります。

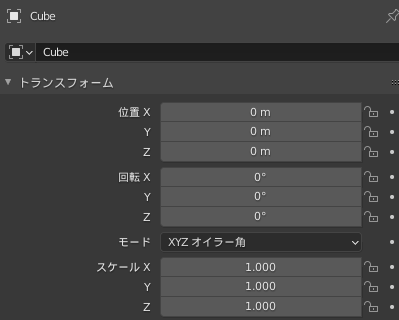
Blender等3Dソフトをいじった方なら馴染み深いですが、3Dオブジェクトの変形はある基準となるオブジェクト（立方体、球など）があったときに「スケール、移動、回転」の3要素で表されます。例えばBlenderの「トランスフォーム」の部分を見ると、まさに3要素から構成されるパラメーターとなっています。

**位置＝移動（Translate）、回転（Rotation）、スケール（Scale）**に対応します。変形を$\mathbf{T}$とすると、

\mathbf{T}=\{\mathbf{s}, \mathbf{t}, \mathbf{R}\}

で表されます。$\mathbf{s}$がスケール、$\mathbf{t}$が移動、$\mathbf{R}$が回転を表します。ここで$\mathbf{s}, \mathbf{t}\in\mathbb{R}^3$のベクトルです。Blenderの表記見れば一目瞭然ですよね。$\mathbf{R}\in SO(3)$は3×3の回転行列。いくら回転しても、どの軸で回転しても最終的には3×3行列に帰着できます。これは二次元の回転と同じです。

回転はアフィン変換の関数で処理されることが実用上多いですが、そもそもスケールも移動も定義上はアフィン変換なので、$\mathbf{T}$はアフィン変換です。アフィン変換同士は合成できるので、$\mathbf{T}$は3×3行列として表現できます。これを$k(\mathbf{x})$とすれば、

k(\mathbf{x})=\mathbf{R}\cdot \begin{bmatrix}s_1 & & \\ & s_2 & \\ & & s_3 \end{bmatrix}\cdot\mathbf{x}+\mathbf{t}\tag{6}

この変換はオブジェクトの点→シーンへのものです。画像データとして観測されているのは、「もととなるオブジェクトに何らかの変換が加えられたときの、レンダリングされたシーン」なので、（オブジェクトの移動とは独立した）正規のオブジェクトの特徴$\mathbf{f}$を求める必要があります。これ求めるには、$k^{-1}(x)$という逆変換を適用する必要があります。実装上は逆行列を求めるだけなので単純です（アフィン変換で表現したかったのはこれが理由です）。

実践的には、正規のオブジェクト空間（canonical object space）で特徴を評価し、オブジェクトの移動が与えられたシーンの空間でボリュームレンダリングを行います。これは「オブジェクトの変形のパラメーターの影響を排除して、オブジェクト固有の表現を獲得したい」のだなと、解釈できます。

$$(\sigma, \mathbf{f})=h_\theta\Bigl(\gamma(k^{-1}(\mathbf{x})), \gamma(k^{-1}(\mathbf{d})), \mathbf{z}_s, \mathbf{z}_a\Bigr)\tag{7}$$

同時にこれは1つのシーンに複数のオブジェクトを配置することが可能になります。

シーンの統合

オブジェクトのスケールや移動のコントロール

今シーンに$N$個のエントリーがあるとします。$N$個のエントリーのうち、1個は背景で、残る$N-1$個はオブジェクトです。

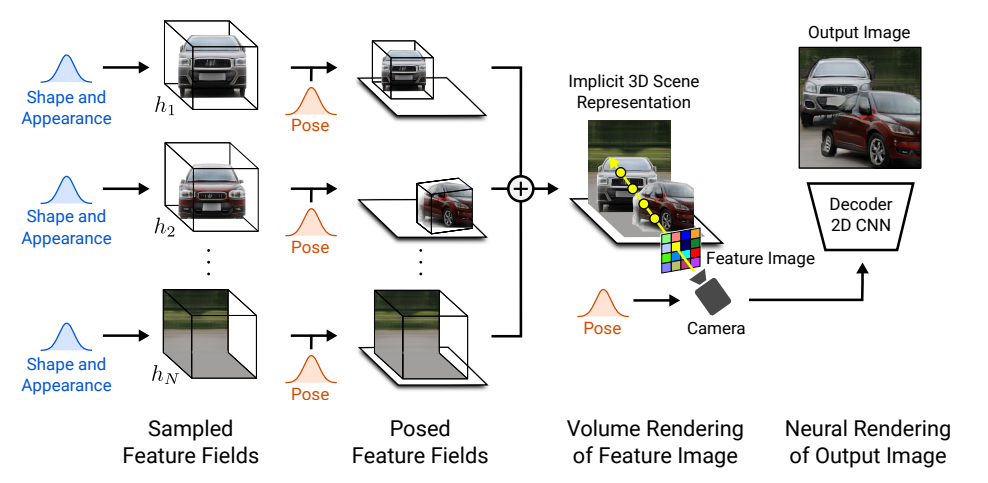
全体のアウトラインはこのようになります。「Shape（形状） and Appearance（外観）」というのは、$\mathbf{z}_s, \mathbf{z}_a$に対応¹し、オブジェクトごとに定義します。

複数のエントリーへの拡張

ところで式(6)の$k(\mathbf{x})$は、オブジェクトの点→シーンへの変換でしたので、実際は変形のパラメーター$\mathbf{s, t, R}$よって条件付けられた、$k(\mathbf{x}|\mathbf{s, t, R})$であることがわかります。$\mathbf{s, t}$についてエントリー数$N$ごとに別々にパラメーターをもたせ、$\mathbf{s}_N, \mathbf{t}_N$とするように拡張します（なぜか回転は拡張していません）。

デモ動画ではボールや自動車を動かしていましたが、このパラメーター拡張によって、オブジェクト単位の移動が実現できるようになっています。式(7)をこの拡張にあわせると（これは自分が勝手に書いたものなのでこの表記があっているかはわかりませんが）、

$$(\sigma^N, \mathbf{f}^N)=h^N_\theta\Bigl(\gamma({k^N}^{-1}(\mathbf{x})), \gamma({k^N}^{-1}(\mathbf{d})), \mathbf{z}^N_s, \mathbf{z}^N_a \Bigl| \mathbf{s}_N, \mathbf{t}_N\Bigr)\tag{8}$$

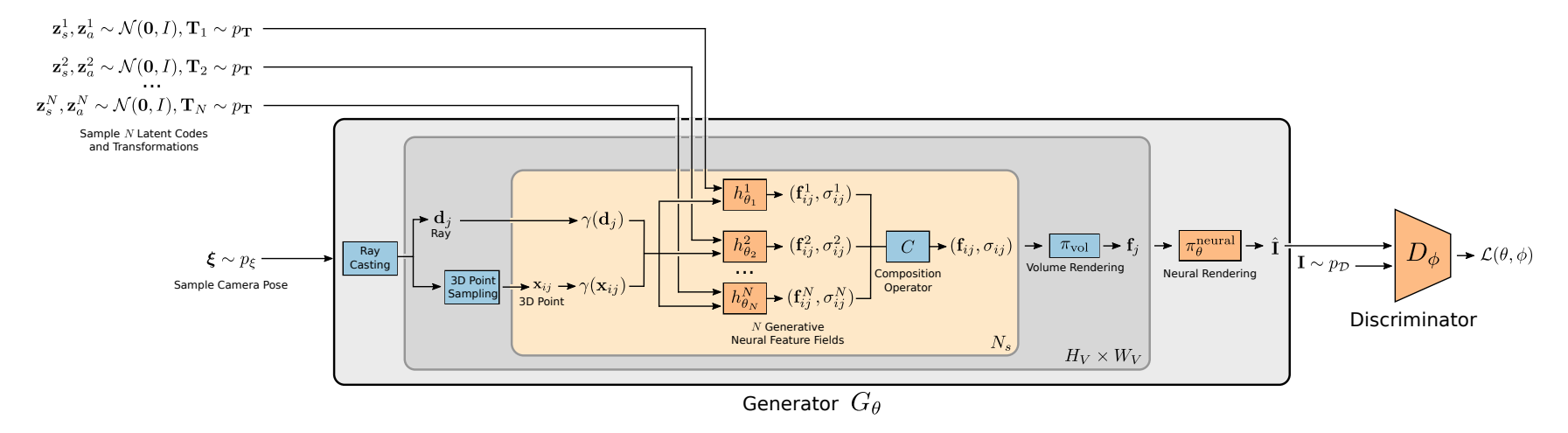
と表記できるのではないかと思います。あくまで$\mathbf{x, d}$はカメラ固有の値で、オブジェクトの移動は$\mathbf{s}_N, \mathbf{t}_N$で表現します。アウトラインは以下の図になります。

凝ったスタイルはないものの、過不足なく表している良い図で、$N$個のエントリーに対して、形状と外観の乱数$\mathbf{z}^N_s, \mathbf{z}^N_a$、オブジェクトの変形$\mathbf{T}_N$を与えます。$h_\theta^N$では、$\mathbf{T}_N$によらない正規のオブジェクト（オブジェクトの固有表現）を学習し、$\mathbf{T}_N$によってアラインメントされた特徴量$(\mathbf{f}_{ij}^N, \mathbf{\sigma}_{ij}^N)$を得ます。

ここで$ij$は「レイ上のサンプリング点×レイの数」を表すものと考えられます。最初ボクセル上の座標かと思ったのですが、レイ上の座標に置き換えられているようです。レイキャスティングとは、先程見たようにカメラの位置からいくつものレイを投射するものでした。レイは開始地点が同じで方向だけ変わるので、$j$番目のレイは$\mathbf{b}_j$で表されます。

ボリュームレンダリングの説明で、レイを上から見下ろすような図を紹介しましたが、あれは特定のレイにおけるサンプリング点の集合です。あるレイ$\mathbf{b}_j$に対し、サンプリング点を$N_s$作ります。そのサンプリング点のインデックス$ij$です。つまりここでの$(\mathbf{f}_{ij}^N, \mathbf{\sigma}_{ij}^N)$は何を表すのかというと、

• $\mathbf{f}_{ij}^N$：$\mathbf{b}_j$のレイにある$i$番目のサンプリング点の、$N$番目のエントリーに対する（RGB値のような実際はもっと次元数の多い）特徴量
• $\mathbf{\sigma}_{ij}^N$：$\mathbf{b}_j$のレイにある$i$番目のサンプリング点の、$N$番目のエントリーに対する（不透明度のような実際はもっと次元数の多い）Volume density

にあたります。これらをエントリー数$N$の周りで足し合わせて（Composition Operator）、全体の特徴量を計算し、ボリュームレンダリング→ニューラルレンダリングします（詳細は後述）。これで、カメラの位置に対する2Dのレンダリング画像ができるというアウトラインです。

学習可能なパラメーターが少ない

GIRAFFEの特徴として、Conv2DやLinear（Dense）といったニューラルネットワーク特有の学習可能なパラメーターがほとんどない点があります。Generatorのコードを見ると驚くのですが（なにがやっているのを理解するのは大変なので流し見程度がいいです）、ニューラルネットワークの層がなく、ほとんどPyTorchの関数で行列計算を決定的に行っているのがわかります。

これはいわゆる3Dレンダリングソフトがやっている実装をPyTorchベースで表現したもので、全体図の青のブロックがそれにあたります。一方で学習可能な係数を持っているのはオレンジのブロックのみです。後で確認しますが、従来のGANと比べて圧倒的に少ない係数で動いているのがGIRAFFEです。

Composition Operator

「Composition Operator」では$N$個のエントリー周りについて統合をします。$i$番目のエントリーについて考えます。$h_{\theta_i}^i$のよって推定された、Volume density$\sigma_i\in\mathbb{R}^+$と、特徴ベクトル$\mathbb{f}_i\in\mathbb{R}^{M_f}$があります。ここでのVolume densityと特徴ベクトルは、カメラのパラメーター$(\mathbf{x, d})$によってアラインメントされたものなのでComposition Operatorを$C(\mathbf{x, d})$とすると、

C(\mathbf{x, d})=(\mathbf{\sigma, f})=\Bigl(\bar{\sigma}, \frac{1}{\bar{\sigma}}\sum_{i=1}^N\sigma_i\mathbf{f}_i\Bigr), \qquad \bar{\sigma}=\sum_{i=1}^N\sigma_i\ \tag{9}

と表現できます（論文の式がややこしかったので少し表現変えました）。Volume densityの統合は単なる平均、特徴ベクトルの統合はVolume densityによる重み付け平均です。

シーンレンダリング

3Dのボリュームレンダリング

ここでようやくボリュームレンダリングになります。ここでのボリュームレンダリングはRGB値の直接の推定ではなく、$M_f$次元の特徴量$\mathbf{f}$のレンダリングです。$M_f=3$とすれば普通のボリュームレンダリングです。計算方法は特に変わらないので特段変わったことはしません。

今、カメラの状態$\xi$に対し、ある$\mathbf{d}$方向にレイが与えられたとしましょう。レイ上のサンプリングポイントを${\mathbf{x}_j}_{j=1}^{N_s}$とします。$N_s$はサンプリング数です。先程の説明では、$i$が同一レイのサンプリング、$j$がレイのインデックスを表していましたが、インデックスが式との間で衝突してしまったようで、論文表記だと逆転しています。

ボリュームレンダリングでやりたいのは「レイの数 × サンプリング数$N_s$」のサンプリング方向の軸を統合して「レイの数」という次元にしたいのです。式で表せば、あるレイに対し、

\pi_{\rm{vol}}:(\mathbb{R}^+\times \mathbb{R}^{M_f})^{N_s} \to \mathbb{R}^{M_f}, \quad \{\sigma_j, \mathbf{f}_j\}_{j=1}^{N_s}\to\mathbf{f} \tag{10}

ここで式(10)の$\mathbf{f}$はあるレイについての特徴量ですが、これらのレイは投射したスクリーンに対するピクセルに相当します。つまり、各レイは投射された2D画像の（粗い）1ピクセルとみなせます。ただ、実際は出力画像の解像度よりももっと少ない数のレイにするので、後の「Neural Render」モジュールで超解像度のような処理を行います。

ボリュームレンダリングの数値計算の式を用い（『Optical Models for Direct Volume Rendering』という論文が元）、

\begin{align}\mathbf{f}&=\sum_{j=1}^{N_s}\tau_j\alpha_j\mathbf{f}_j \\ \tau_j&=\prod_{k=1}^{j-1}(1-\alpha_k)\\ \alpha_j&=1-e^{-\sigma_j\delta_j} \\\delta_j&=\|\mathbf{x}_{j+1}-\mathbf{x}_j\|_2\end{align}

と計算されます。何の式だか意味不明ですが、普通のボリュームレンダリングの式(1)を再掲すると、

$$I=\int_0^D c(x(\lambda))e^{-\int_0^\lambda \alpha(x(\lambda'))d\lambda'}d\lambda \tag{1}$$

であるため、連続関数の積分を離散化したものと理解できます。数学的な理論展開が気になる方は元の論文を読んでください。理解のために、$\delta_j=\delta$と一定値で表せるように簡略化してみると、

$$\tau_j=\prod_{k=1}^{j-1}e^{-\sigma_k\delta}=-\exp\Bigl[\sum_{k=1}^{j=1}{\sigma_k\delta}\Bigr]$$

と簡単な式で表すことができます。これは∫がΣに置き換わっているので、まさに積分の離散の場合です。

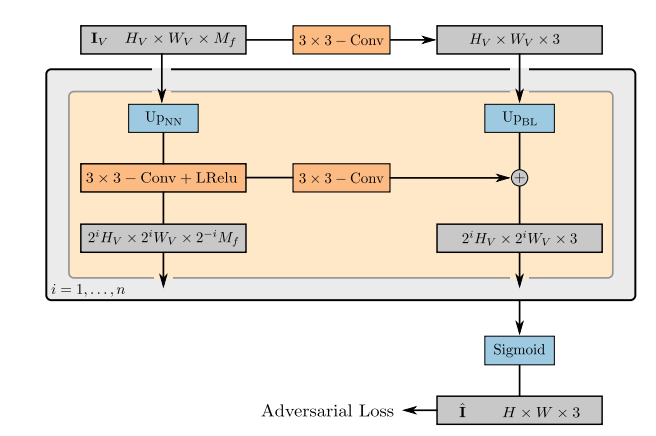
なお、このボリュームレンダリングによって得られた画像（特徴マップ）の解像度は$16^2$と、本来の解像度よりも粗い解像度になっています。実際に出力するRGBの投射画像は$64^2, 256^2$といった解像度とします。ここに変換するのが次に説明する「2D Neural Rendering」のモジュールです。

2D Neural Rendering

ニューラルレンダリングのオペレーターを

$$\pi_\theta^{\rm{neural}}: \mathbb{R}^{H_V\times W_V \times M_f}\to \mathbb{R}^{H\times W\times 3}$$

とします。ここは普通のニューラルネットワークで、$\mathbf{I}_V\in\mathbb{R}^{H_V\times W_V \times M_f}$を最終的な合成画像$\hat{\mathbf{I}}\in\mathbb{R}^{H\times W\times 3}$にマッピングするモジュールです。論文の図を見るのがわかりやすいです。

$U_{P_{NN}}$はNearest Neighborによる拡大、$U_{P_{BL}}$はBilinearによる拡大を示します。

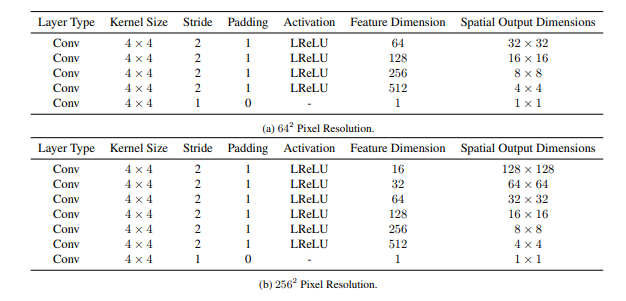
Discriminatorの構造

Dは普通のConvNetです。合成画像の解像度によってモデル構造が違います。4×4のカーネルという、偶数の畳み込みカーネルを使っているのが珍しいです。

ハイパラ設定

今までの内容を振り返る意味からもハイパラを見ていきましょう。

• ${h_{{\theta}_i}^i}_i^{N-1}$：形状と外観の乱数、オブジェクトの変形の行列、カメラのパラメーターが与えられたときのオブジェクトの特徴場。オブジェクト間で重みは共有し、MLP＋ReLUで構成。8レイヤーで隠れ層の次元は128とする。出力はVolume densityの$\sigma^i$、特徴量$\mathbf{f}^i$でそれぞれ1、$M_f=128$次元。背景の特徴場$h_{{\theta}_N}^N$については、次元と層の数を半分にする（オブジェクトとは別の重みにする）。
• カメラのPositional Encodingの$L$の数は、座標の$\mathbf{x}$で10、方向の$\mathbf{d}$で4
• 1つのレイに対するサンプリング数$M_s=64$
• 3Dのボリュームレンダリング（2Dニューラルレンダリングの前）の特徴マップ$\mathbf{I}_v$の解像度は16
• Generatorの係数に0.999でDecayする移動平均つき
• バッチサイズ32のRMSProp。Dの学習率は1e-4、Gの学習率は5e-4
• 解像度が$256^2$で出力するときは$M_f=256$とし、Gの学習率を2.5e-4とした

データセット設定

データセット設定が面白くて、最初自分はカメラのパラメーターと画像が紐付けられたデータでしか訓練できないのかと思ったのです。ただそんなことはなく、CelebA HQやFFHQ、LSUN ChurchesといったこれまでのGANで使われていたデータセットに対しても生成成功しています。

最初はいきなり普通の画像でやらずに、「Chairs」というデータセットで行っています。これは3Dソフトで様々な角度からレンダリングされた画像です。これは「Chairs」の論文からです。

挑戦的な試みとして1つのオブジェクトで、リアルな世界のデータセット（LSUN Churches、FFHQ、CompCars）でもトライしています。CompCarsとはこのようなデータです（公式サイトからの引用です）。

CompCarsではオブジェクトの位置のバリエーションを出すためにRandomCropを導入しています。個人的に不思議なのは、このような単一オブジェクトあたり1つの視点から撮られていないデータセットでも、カメラの位置、オブジェクトの位置やスケールといったパラメーターをコントロール可能な表現を獲得できていることです。これらのパラメーターは訓練時には乱数で入力していましたが、そんなアバウトなやり方でもDisentangleしてくれるというのがGIRAFFEのとても不思議なところです。似た感覚は最初にDCGANを見たときも感じたので、慣れれば当たり前になるのかもしれません。

CompCarsに対してどの程度の生成が可能になったかは、プロジェクトページにも動画としてまとまっています。CompCarsはデータセット全体で見れば、いろんな視点から車を撮っていたのでうまくいったのかもしれません。

論文としてはリアルのデータと、合成データを行ったりきたりしており、まだ「視点やオブジェクトの位置でほぼほぼOne-shotなリアルなデータ」を前提とした想定ではなさそうです。これは「Clevr-2345」というデータセットに対して、訓練の進みを可視化した図です。

訓練のかなり早い段階で、教師なしのDisentangleに成功しています。こういった合成データに対しては成功率が高そうです。

教師なしでどの程度コントロールできるか

「教師なしでDisentangle」でこの論文のテーマになっていますが、いろんな項目に対してDisentangleしようとしているのがわかります。

• 背景とオブジェクト
• 個々の物体の回転や平行移動、形状や外観
• カメラの仰角の変更
• 形状を変えずに外観のみ変更
• 学習データの分布外のパラメーターの生成

訓練データを超えたデータに対する生成です（左）。これはネットワークを単なるCNNのモデルとしてやるだけではまず不可能で、3Dのレンダリングプロセスを相当決め打ちして、コントロール可能なパラメーターを導入したおかげだと思われます。「構成されたシーン表現」をGANに導入するのが大事なのでしょう。

右が先行研究との比較です。物体の回転で差がわかりやすいです。同じNeRFベースのGRAFでは、回転角によっては車の形状に大きな歪みが生じています。GRAFとの大きな違いは、ボリュームレンダリングをRGBでダイレクトにやらずに、もっと次元数の大きい特徴マップに対して行うということでしたので、GRAFのようにRGBでやると表現が足りていないことがわかります。

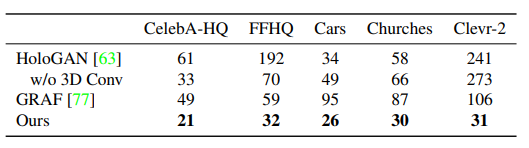
定量評価は生成画像のFIDでやっています（低いほうが良い）です。見て明らかなレベルなので、定量評価貼るまでもないと思いますが、一貫して先行研究より良いです。

計算量も軽い

GRAFとの大きな違いは次元数だけではなく、計算量とも関係しています。GIRAFFEのボリュームレンダリングは「16×16」という低解像度の特徴マップを出力し、あとはCNNで解像度を引き上げるというものでした。

実際にGRAFと比較すると、レンダリング速度が64×64で110.1ms→4.8ms、256×256が1595.0ms→5.9msと大幅に改善しています。

またGIRAFFEはモデルの係数が少ないことも特徴で、Generatorのパラメーター数は0.41Mです。

こんなに少ないパラメーター数で教師なし3D-Disentangleができるというのは、今までの2DGANばかり見てきた自分にとってはにわかには信じがたいのです。Disentangleが強いGANといえばStyleGANの系列でしたが、それでもこんな少ない係数ではできないですし、3Dの物体の変形を定義はまずできなかったと思われます。

訓練時はカメラや変形のパラメーターが乱数？？

個人的に一番気になったのは、「なぜカメラのパラメーターや、オブジェクトの変形行列が与えられていないにも関わらず、最終的にそれらに関してコントロール可能な表現を獲得できているのか」という点です。多分これを紐解くには訓練時にコードを見る必要がありそうです。

Generatorのforwardの関数を見てみましょう。

    def forward(self, batch_size=32, latent_codes=None, camera_matrices=None,
                transformations=None, bg_rotation=None, mode="training", it=0,
                return_alpha_map=False,
                not_render_background=False,
                only_render_background=False):
        if latent_codes is None:
            latent_codes = self.get_latent_codes(batch_size)

        if camera_matrices is None:
            camera_matrices = self.get_random_camera(batch_size)

        if transformations is None:
            transformations = self.get_random_transformations(batch_size)

        if bg_rotation is None:
            bg_rotation = self.get_random_bg_rotation(batch_size)

        if return_alpha_map:
            rgb_v, alpha_map = self.volume_render_image(
                latent_codes, camera_matrices, transformations, bg_rotation,
                mode=mode, it=it, return_alpha_map=True,
                not_render_background=not_render_background)
            return alpha_map
        else:
            rgb_v = self.volume_render_image(
                latent_codes, camera_matrices, transformations, bg_rotation,
                mode=mode, it=it, not_render_background=not_render_background,
                only_render_background=only_render_background)
            if self.neural_renderer is not None:
                rgb = self.neural_renderer(rgb_v)
            else:
                rgb = rgb_v
            return rgb

とても単純なコードで、実際のレンダリングプロセスはself.volume_render_imageやself.neural_rendererで行っています。

ポイントとなるのは、camera_matrices is Noneやtransformations is Noneのケースです。FFHQやCelebAの場合、データセットにこれらのパラメーターがないので「どうやって訓練させるか」がすごい気になったのです。これらのパラメーターがない場合は乱数で訓練させています。

「ない場合は乱数でやる」というのはわかったのですが、もし合成データなどでパラメーターがとれた場合はどうしているのでしょうか。これはtraining.pyのコードを見るとわかります。

    def train_step_generator(self, data, it=None, z=None):
        generator = self.generator
        discriminator = self.discriminator

        toggle_grad(generator, True)
        toggle_grad(discriminator, False)
        generator.train()
        discriminator.train()

        self.optimizer.zero_grad()

        if self.multi_gpu:
            latents = generator.module.get_vis_dict()
            x_fake = generator(**latents)
        else:
            x_fake = generator()

        d_fake = discriminator(x_fake)

Generatorのforwardの部分を見てみましょう。if self.multi_gpuは複数GPUのためのコードなので無視していいです。訓練時はx_fake = generator()としているのがわかります。引数を何も与えない場合は乱数で訓練されるので、**データセットの如何に関わらず、訓練時はカメラのパラメーターや変形行列は何も与えていない（乱数として訓練させている）**という衝撃の事実がわかりました。

よく考えると、訓練時にカメラや変形行列を与えていたら「Conditional GAN」と呼ばれるはずです。例えば2DGANのACGAN（クラスのラベルを訓練時に与える）は典型的なConditional GANですが、Conditional GANだったら教師なしでDisentangleという表現は使わないはずです。カメラや変形のパラメーターを乱数で与えているからこそ、教師なしと呼べるのです。この事実に気づいたので、個人的には腑に落ちました。

このモデルの限界

個人的に疑問だったのが「これデータセットによってうまくいくかどうか相当変わるな」という点です。どういった点に限界があるのかという点は、論文にも書かれています。

データセットのバイアス

データセットに固有のバイアスがある場合、変動要因を分離するのに困難するとのことです。下の図はCelebA-HQですが、圧倒的にカメラ目線の画像が多いため、回転させると目や髪の向きが固定されてしまいます。

オブジェクトの変形の分布

このモデルでは、カメラのポーズやオブジェクト変形を一様分布と仮定して訓練していますが、データセットの実際の分布とミスマッチが問題となることがあります。例えば、背景に境界があるChurchや、前景が背景を含むCompCarsでは、背景と前景の分離に失敗することがあります。

これを見ていると、背景と前景のテクスチャが似ていると起こりやすいのでしょうかね。このミスマッチを解消をするための分布設計については、本論文では「今後の課題」としています。

まとめと感想

この論文では、これまでの2DGANの枠組みを飛び越えて、「カメラの位置や角度」「オブジェクトのスケール、移動、回転」「オブジェクトの形状や外観」を、データセットによる追加の教師なしで3Dレンダリングベースで生成できるという衝撃的な内容でした。「これはBest Paper Awardsとるわ」って感じの内容で、細部を読み込んでいるとあまりにその凄さに震え上がった内容でした。

基本となる枠組みはボリュームレンダリングという、従来の3Dレンダリングをベースとしています。3Dレンダリングの枠組みをGANに導入するだけでこれだけのすごいことが起こるので、今後こういうアプローチが流行っていくと思います。3Dレンダリングの部分の知識がなくて、付け焼き刃で調べたのですが、ここが複雑になっていくとだんだんついていくのが大変になっていくので、「GIRAFFE程度で勘弁してください」という気持ちは多少ありました。

今までGANのDisentangleというと、3日目に紹介したような「StyleGANを訓練してその潜在変数をいじる」というようなケースが有望なやり方でした。StyleGANの場合は訓練したモデルがあり、その潜在変数を解釈・操作するというとてもボトムアップな方法です。NeRFもそうですが、GIRAFFEの場合は、「こういう操作をしたいから、3Dレンダリングをベースとしたこういうフレームワークを作って訓練」というかなりトップダウンなやり方です。事実、計算量パラメーターのコントロール可能性でもうまく行っています。GANの論文が出たのが2014年ですが、たった7年でここまで進化するなんて驚きですね。もう5年ぐらいしたら3Dのゲーム画面みたいなGANができているかもしれません。

感想としては「とにかく読むのが難しいけど、それに見合った感動は与えてくれる」という不思議な論文した。「なんで乱数から訓練して、形状や変形を学習できるの？」という不思議な感覚は、最初にDCGANを見たときのそれをまさに思い出させるようで、懐かしい感覚になりました。難しい概念ながら、論文がとにかく丁寧に書かれていて、「論文をよむのが一番早いし楽」というのがとても良かったです。ただ実装は相当沼なので、1から実装はやめておいたほうがいいと思います（3Dレンダリングの部分がうまくライブラリになれば楽になりそう）。

GIRAFFEの解説いくつか散見されるのですが、ここまで突っ込んで読んだ記事は多分日本で（もしかしたら世界でも？）自分が初めてだと思われるので、NeRFの系列も含めて皆さんの参考になれば幸いです。

告知

このアドベントカレンダーが本になりました！
https://koshian2.booth.pm/items/3595424
Amazonでも扱いあります詳しくは👉　https://shikoan.com

1. あくまで自分の勝手な想像ですが、形状と外観を分けて定義しているのは、一般的な3Dのオブジェクトがメッシュとテクスチャのように、形と外観を独立して管理しているからだと思われます。将来的にはそういった拡張をしたいのかなと思いました。 ↩