はじめに

このプロジェクトは私が学生時代のアルバイトで某企業で働いていた時テキスト文の過去データを元にテキスト分類を行った記録である。記録として残しておきたいのでQiitaに投稿しました(20201212-1)

流れとしては、前処理→SVM→GridSearch→精度評価(混合行列・ROC曲線・acuuracy)の説明とプログラムを掲載しています！機械学習初めての方にとってはとても良い教材になるかと思います。

背景

背景としてその企業では毎年社内向けにあるコンテストが行われる(記事にもなってる)。そのコンテストにルールで決まった定型のテキスト文でエントリーをたくさん寄せられていた。所属していた部署ではそのテキスト文を審査する部署で、審査を過去のテキスト文の審査結果であるGood,Badのフラグを元に機械学習を用いて振り分けできないかというアイディアのもと始まった。振り分け後その結果によって人の審査するチェック数をエントリーごとに振り分けることによってチェック数の削減になることが期待される。

使ったデータの説明

※データは守秘義務のため見せることはできませんがプログラムは一部抜粋で紹介します。

テキスト文(過去2年分のデータ):あるルールに従って作られたテキスト文2年分(計2379件)
Good/Badフラグ:それぞれのテキスト文にGood/Badのようなフラグで判定されているデータ(計2379件)

具体的なデータの詳細

カラム	説明	値
id	行の通し番号	1-2379
text	テキスト文	-----(文字列)----
good	goodフラグ	0,1表記(Goodなら1で定義)
bad	badフラグ	0,1表記(Badなら1で定義)

ダミー変数化しているデータを採用。GoodもBadがついていないデータもある。GoodもBadもついているデータもとても少ないが何件かあった。

GoodとBadの定義であるが、そもそも1案件に審査する人数は3人程度で審査している。そのため同じ案件にGoodとジャッジする人もいればBadとジャッジする人もある案件も出ている状態である。
またGoodとジャッジする延べ件数はBadとジャッジする述べ件数に比べてとても少ないデータになっていた。
Goodが1件でもついたデータはGoodとしてGoodがついていなくBadが1件でもついたデータはBadとして扱った。GoodもBadもついてないデータは区別はしてないがAverageとして扱った。(2020/03/20現在)

(2020/05/13現在)Goodの判別は廃止しBadのみ判別する分類器を作った(Badかどうかを判別する)

カラム	説明	値
id	行の通し番号	1-2379
text	テキスト文	-----(文字列)----
bad	badフラグ	0,1表記(Badなら1で定義)

データの観察・前処理

流れとしては
1)データをimport
2)NAがあったら削除
3)形態素解体(今回はMeCabを使用)
4)Vec化(今回はTf-idfを使用)
5)特徴量のyとの重要度でソートし特徴量を厳選する(今回はSelectKBestを使用)
6)TrainデータとTestデータに分けて分割した(train_test_splitを使用した)

以下順番に説明を示す。

1)データをimportするプログラム部

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy as sc
import MeCab
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest

前処理で必要なモジュールは上述で記載したモジュールである。

2)NAがあったら削除

今回扱ったデータは完全データだったので気にしなくても大丈夫だったが、完全データでないとTfidfの時に自分の場合はエラーが出たのでNAを削除するプログラム(以下)を行うことを推奨する。

df = df.dropna()

3)形態素解体(今回はMeCabを使用)

形態素解体とは「自然言語で書かれた文を言語上で意味を持つ最小単位(＝形態素)に分け、それぞれの品詞や変化などを判別すること」をいう。(形態素解体とは)
色々パッケージは種類あるが今回のプロジェクトではMeCabを使用した。以下形態素解体のプログラムである。

#NAは削除した状態とする。
#データの形はテキスト文のみをリスト型で集めたデータの形を取っている。

wakachi_list = []
for i, di in enumerate(df_total_X):
    try:
        w = m0.parse(di)
    except:
        w = di   
    if 'list' in str(type(w)):
        #print('No.', i, w[:30])
        wakachi_list += [w.split(' ')]
    else:
        #print('X No.', i, w)
        wakachi_list += [w]

わかち書きされたテキスト文はwakachi_listに組み込まれていくようなプログラムになっている。

4)Vec化(今回はTf-idfを使用)

わかち書きしたテキスト文について学習できるようにベクトル化する必要がある。こちらも何パターンもある。今回はTf-Idfを採用した。Tf-Idfの強みとして、「いくつかの文書があったときに、それらに出てくる単語とその頻度(Frequency)から、ある文書にとって重要な単語はなんなのかというのを数値化します。」(TF-IDF)

#NA無いとstopする。
#dropna()を行う必要がある。

vectorizer = TfidfVectorizer(use_idf=True, token_pattern=u'(?u)\\b\\w+\\b')
vecs = vectorizer.fit_transform(wakachi_list)

5)特徴量のyとの重要度でソートし特徴量を厳選する(今回はSelectKBestを使用)

TF-IDFの特徴として文章のサンプル数が多いとベクトルの次元数が増えることが起こる。ここで目的変数(y)と最も関係性が強い特徴量を選択して関係性が弱い特徴量を削除して減らすことでより学習で精度upを期待できると考え特徴量を厳選することを行った。以下プログラムで解説する。(【Python】わかりやすくSelectKBestを解説！)

#今回はvec化した時24582次元になったため今回は1/10の2500次元にした。
skb = SelectKBest(k=2500)
res2 = skb.fit_transform(vecs_train,y)

設定する次元数が極端に少ないと学習で使うパラメータの数が少ないため学習しやすい反面、重要である特徴量まで削除してしまう可能性がある。
設定する次元数が多いと学習に使うパラメータよりも余分に採用していることになるのでそもそも効率が悪くなる可能性がある。

この設定方法もトライ&エラーを重ねていい調整を見つける必要がある。

6)TrainデータとTestデータに分けて分割した(train_test_splitを使用した)

TrainデータとTestデータに分けてTrainデータで学習しモデルのパラメータを作成する。出来上がったパラメータをtestデータに当てはめて精度を検証した。この分割に関して自分は70%をTrainデータ,30%をTestデータとして採用した。この分け方も人によって好みが分かれるところであるので変更する必要がある。

#res2はXベクトルの2500次元に整形したデータを格納している
#yは目的変数(今回はこのBadなら1,Badでないなら0としている)

vecs2_train, vecs2_test = train_test_split(res2, random_state=0,train_size=0.7)
y_train, y_test = train_test_split(y, random_state=0,train_size=0.7)

random_state=0とするとシャッフルの分割を記憶して何度行っても同じsplitでできるのでとても便利である。

ここまでが前処理として行った内容である。

データの学習・評価

1)学習のモデルで使うモジュールをimport
2)クロスバリデーション
3)SVM
4)GridSearch
5)精度評価について

1)学習・評価のモデルを使うモジュールをimport

今回学習で使ったモジュールは以下の通りである。今回はクロスバリデーション(cv=10)付きのSVM&GridSearchを行った。評価で用いた指標はメインで混合行列とROC曲線を採用した。サブとしてaccuracyを見るような形で評価することした。


from sklearn import svm
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
from sklearn.metrics import confusion_matrix

2)クロスバリデーション

クロスバリデーションとはTrainデータを解析者が決めたNで等分に分割してある1部分をTestデータとし残りをTrainデータとし、それをN回Testデータとして変更しN個できたモデルに関して出てきた結果において精度の平均を算出する手法である。よく使われることとしてNが少ない時によく使われる手法である。(詳細はこちらを参照:クロスバリデーションとは)

※プログラムの都合上4)に付属しているため4)のプログラムの説明の時に同時に説明する。

3)SVM

サポートベクトルマシン(svm)は汎化性能や応用分野の広さから、データ分析の現場でよく用いられる機械学習のアルゴリズムの一つです。マージン最大化と呼ばれる考え方を用いて主に2クラス分類問題で用いられることが多い。2スラス分類を応用することで、他クラス分類や回帰問題などにも応用することが可能である。(詳細はこちらを参照:[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく①～理論と数式編～)

続いて今回書いたプログラムを掲載する。

svm_tuned_parameters = [
    {
        'kernel': ['rbf'],
        'gamma': [0.076],
        'C': [40],
     'probability':[True]
    }
]

kernelを変更することで線形で分類するのではなくN次元の超平面において任意の曲線で分類することも可能である。またそのほかにもオプションでいろいろカスタマイズすることができるので必要に応じて変更していくことでできる。
今回は(4)で説明するGridSearchを行い網羅的にパラメータを変更しそれぞれでモデルの精度を考え、ベストな精度を模索する手法を採用しているため値は私が使ったデータにおいてベストだと判断したパラメータの値になっているので、それぞれのデータに合うようにパラメータチューニングを行う必要がある。

4)GridSearch

Gridsearchとは、scikit-learnに含まれているモジュールでハイパーパラメータ探索用のGridSearchCVというものである。Pythonのディクショナリでパラメータの探索リストを渡すと全部試してスコアを返してくれるので非常に便利である。パラメータを細かく切ることにいよってベストなパラメータを発見することができるが、そのぶんプログラムを回し終わるのに時間がかかってしまうというデメリットも生じる。

以下プログラムで示す。

print("[INFO] SVM (グリッドサーチ)")
svm_tuned_parameters = [
    {
        'kernel': ['rbf','linear', 'poly'],
        'gamma': [0.5,0.076,0.1,0.2],
        'C': [20,30,40,50,60],
     'probability':[True]
    }
]

gscv2 = GridSearchCV(
    svm.SVC(),
    #penalty='l2',
    svm_tuned_parameters,
    cv=5,      # クロスバリデーションの分割数
    n_jobs=1,  # 並列スレッド数
    verbose=3  # 途中結果の出力レベル 0 だと出力しない
)

このように(3)で前述したSVMのパートにサーチしたいパラメータを入れ、GridSearchCV()という関数内に含めてほか(2)で説明したクロスバリデーション(cvと記述している箇所)を設定したりオプションをつけることが可能である。

学習する時はscikit-learn同じみ(?)の'モデル名.fit(X_train,Y)'で学習させることが可能である。
今回の作ったプログラムで例として掲載すると

rongai = y_train.tolist() #そのまま行なったらエラーがでたためlist化した
gscv2.fit(vecs2_train, list(rongai))

これで学習させることが可能である。
学習が終わった後行わないといけない作業として、ベストなパラメータを使ったモデルを取ってきて新たな変数に格納して記憶させておく必要がある。このプログラムは以下でできる。

svm2_model = gscv2.best_estimator_  # 最も精度の良かったモデルのパラメータを取って来ることができる
print(svm2_model) #パラメータをプリントできる

GridSearhの良い使い方として、時間があれば大雑把にパラメータをチューニングした後、その近辺でまたGridSearchを行なってみるといったように何度かパラメータを変更して行うことで神のみぞ知るベストなパラメータに限りなく近いパラメータを見つけて結果的にベストに近い精度upを見込むことが可能である。

5)精度評価について

今回使った精度評価の指標は混合行列とROC曲線をメインで用い、サブの指標としてaccuracyを用いた。それぞれ説明を行なっていく。

5-1混合行列について

混合行列とは分類問題でよく用いられる評価指標の一つである。今回は基本的な2×2混合行列で説明を行う。

混合行列	予測して1	予測して0
データの正解1	TP(True Positive)	FN(False Negative)
データの正解0	FP(False Negative)	TN(True Negative)

この行列を用いることで視覚的にどれほど正解ラベルと誤っているのかを見ることができる。(詳しくはこちらを参照:混同行列(Confusion Matrix) とは〜 2 値分類の機械学習のクラス分類について)

5-2ROC曲線について

ROC曲線とは、混合行列を作る前段階で考えるカットオフ値(機械学習によって得られた確率を参照しこの値よりも上なら1と判断すると決める区切りの点)を変更してみることを考えその結果においてそれぞれ混合行列を書くこともできる。その混合行列の表のTPとTNの和を計算することで良い分類機かどうかを判定することが可能になる。そのTPとTNの和の関係をグラフ化した曲線をROC曲線と呼ぶ。(これは医学や統計分野でよく使われている評価指標である)
(詳細はこちらを参照:機械学習の評価指標 – ROC曲線とAUC)

5-3acuuracyについて

acuuracyとは5-1の混合行列の表で考えると$\frac{TP+TN}{TP+FN+FP+TN}$とかけるものである。簡単にいうとこれは正答率にあたるものである。学習によって導かれた結果がどれくらい正解しているのか簡単にわかる指標である。(詳しくは5-1混合行列の参照として掲載した混同行列(Confusion Matrix) とは〜 2 値分類の機械学習のクラス分類についてを参照してください。)

社員さんに言われて印象に残っていることとして「機械学習の精度がとても良いからといって必ずしもビジネスで用いて良いかといったらそうではないかもしれない」と言われました。私はアルバイトの身であるのでいつかは辞めて他の誰かに引き継ぐことになるので、引き継いだ後の人も同じように結果を再現できたり、総合的に考えて使えるかどうかを判断しないといけないということが重要だと言われたことが印象に残っていて、このプロジェクトを行うときに常に考えながら行いました。

以下プログラムで1~3を説明する。

##5-1混合行列
sss = svm2_model.predict(vecs2_test)
cm = confusion_matrix(y_test, sss)
cm

#テストデータに当てはめた結果
array([[142,  75],
       [ 27, 220]])

##5-2ROC曲線
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc

# AUCの算出
fpr, tpr, thresholds = roc_curve(df5_test, y_pred)
roc_auc = auc(fpr, tpr)

# ROC曲線の描画
plt.plot(fpr, tpr, color='red', label='ROC curve (area = %.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')

plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="best")

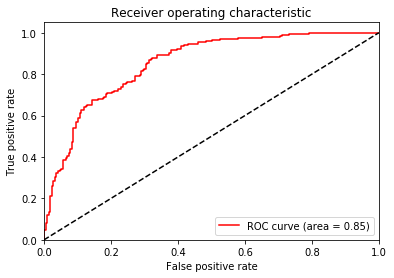
結果はこのような画像でした

AUCという指標が凡例にプリントされていますがAUCは100%に近い方が良いとされています。詳しくは5-2で乗せたROC曲線の参考資料に載せてありますのでそちらを参照してください。

##5-3accuracy
print(svm2_model.score(vecs2_train, list(rongai))) #rongaiがtrainデータの目的変数
rongai2 = y_test.tolist()
print(svm2_model.score(vecs2_test, list(rongai2))) #rongai2がtestデータの目的変数

#結果は以下の通り
0.9166666666666666 #(trainのaccuracy)
0.7801724137931034 #(testのaccuracy)

testデータの精度が78%と分類精度としては良くはないため今後の課題としては考えている。だが78%でGoサインとなった理由として、完全に機械学習のみでシステムを運用するのではなく人もチェックするため誤分類したサンプルは人が補完することで運用できるのではないかという議論になった。そして本プロジェクトはこのシステムを用いて課題はあるが行うことになった。

最後に

ここまで読んでいただきありがとうございます！
これからもコンスタントに投稿しようと考えていますのでLGTM・フォローよろしくお願いいたします！！
また今回は自然言語でしたが画像系も扱っています。ぜひ他の記事もよろしければご覧ください。

そして重ね重ねになりますが、私自身もまだ勉強中の身ですので、質問やアドバイス・ご指摘等ありましたらお願いいたします。

参考

形態素解体とは
 TF-IDF
【Python】わかりやすくSelectKBestを解説！
クロスバリデーションとは
 [機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく①～理論と数式編～
混同行列(Confusion Matrix) とは〜 2 値分類の機械学習のクラス分類について
 機械学習の評価指標 – ROC曲線とAUC

自然言語処理を用いたデータの分類