　機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera　を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。

　第九弾は、異常検知 (Anomaly Detection)、レコメンダシステム (Recommender System)という、実践的な使うアルゴリズムを学びます。異常値を検出するのはデータ解析に必須ですし、レコメンダシステムはネットショッピングでの広告表示などで使われていますね。

異常検知 (Anomaly Detection)

　100人健康診断をしたら数人は病気かもしれません。100個の商品を作れば数個は不良品があるかもしれません。そうした異常値を検出するためのアルゴリズムが、異常検知 (Anomaly Detection)です。

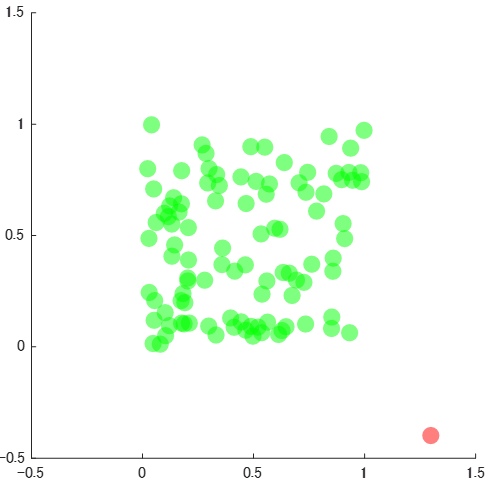
　上のデータで言えば、赤のデータポイントが明らかに外れ値 (Outlier)ですね。

　数学的には、ガウシアン (正規分布)をデータにフィットして、あるデータポイント$x^{(i)}$の正規分布上の値$p(x^{(i)})$が、閾値$\epsilon$より小さければ、外れ値とみなすことにします。

　アルゴリズムは以下のようになります。異常値が入っているかもしれないデータ$x$に対して、そのときの説明変数を$j = 1, ..., n$とすると、

1: 平均値$\mu$を求める。


\mu_j = \frac{1}{m} \sum^m_{i=1}x_j^{(i)}

2: 標準偏差$\sigma^2$を求める。


\sigma_j^2 = \frac{1}{m} \sum^m_{i=1} (x_j^{(i)} - \mu_j)^2

3: 異常値の可能性がある新しいデータ$x_{test}$を用いて、$p(x_{test})$を計算する。


p(x_{test}) = \Pi^{n}_{j=1} p(x_j; \mu_j, \sigma^2_j) = \Pi^n_{j=1} \frac{1}{\sqrt{2\pi} \sigma_j} exp(-\frac{(x_j - \mu_j)^2}{2\sigma_j^2})

4: $p(x_{test}) < \mu$なら、$x_{test}$は異常値と判断。

　正規分布から外れているものを、外れ値とする、わかりやすいですね。

　ただ、データの分布がもともと正規分布ではない場合もあります。そんなときは、$\sqrt{x}$をとったり、$log(x)$をとると正規分布化することができます。色々試してみましょう。

「で、じゃあ閾値$\mu$はどうやって選べばいいの？」

　これは難しい問題で、結局のところ主観的です。砂糖の摂取量も、WHOは1日の総カロリーの5％を掲げてますが、かつては10％でした。

　数学的に決めるには、交差検定 (Cross Validation)を使います。Training Setからモデル$p(x)$を作り、Cross Validation Set/Test Setを用いて、


y = 1 \hspace{15pt} if \hspace{15pt} p(x) < \mu \hspace{15pt} (anomaly)
\\
y = 0 \hspace{15pt} if \hspace{15pt} p(x) \ge \mu \hspace{15pt} (normal)

　のように分類 (Classification)させ、モデル精度を確認します。モデル精度が上がるように$\mu$を決めればいいのですね。

注意点
　異常検知課題では、多くの場合データに偏りがあります (Skewed Data)。異常は全体の一部しかありません。そのため、モデル精度の確認には正答率 (Classification Accuracy)ではなく、F値 (F-score)を用います。「なにそれ？」という人は、過去の記事の下の方を見てください。

レコメンダシステム (Recommender System)

　オンラインショッピング、レストランのレビューサイトなど、ユーザーの行動データから好みを推定し、そのユーザーに合わせた商品なりサービスを提案するアルゴリズムが、インターネット上ではあふれています。こうしたレコメンダシステム (Recommender System)では、通常の機械学習ではない問題に立ち向かわなくてはいけません。

　例えば、2016年の映画について、0 - 5段階で5人にレビューしてもらったとします。すると、以下のようになりました。

　有名な映画ばかりですが、ちょっとジャンルがアニメに偏っていることもあり、全てを観ている人は少ないです。その場合、データは$?$と表現されます。

　ただ、例えば上のデータで言うと井上くんは、「君の名は」「聲の形」という2つのアニメを観て高評価をしていますが、「この世界の片隅に」を観ていません。もし観ていれば、きっと高評価をしているはずじゃないでしょうか。

　一般的に、ユーザー$j$について、まだ観ていないある映画$x^{(i)}$のレビュー $y^{(i,j)}$は、モデルが学習したパラメーター$\theta^{(j)}$を用いて以下のように計算できます。


y^{(i,j)} = (\theta^{(j)})^{\mathrm{T}} x^{(i)}

モデルの学習は、各ユーザー毎に行います。もちろん、そのユーザーが観た映画からしか学習はできないので、各ユーザー、各映画において観ていたら$1$、観ていなければ$0$とする行列$r(i,j)$があると便利です。

　「えっと……映画$x$ってどんなパラメーターなの？」

　パラメーター$\theta$の転置行列との積を取られる運命の$x$は、もちろん行列です。映画なら、各要素を数値化したものです。例えば、$x_1 =$アニメ, $x_2 =$ロマンス, $x_3 =$アクション, $x_4 =$コメディー, ......のように要素を取れば、例えば「君の名は」の$x^{(yourname)}$は、


x^{yourname} = [1.0, 0.9, 0.1, 0.7, ...]

　のようになるかもしれません。

　ただ、このようにそれっぽいパラメーターを与えることはできますが、無数の映画がある中で全部を観てパラメーターを決めるのは大変ですし、そもそも人によってパラメーターの決め方も違うでしょう。「君の名は」を新海監督だから観た人と、Radwimpsが好きだから観た人とでは、$x^{yourname}$の中身そのものが全く違うかもしれないですよね。

　そのため、映画の要素$x^{(i)}$とレビュー$y^{(i,j)}$からモデルパラメーター$\theta^{(j)}$を学習するだけでなく、$\theta^{(j)}$と$y^{(i,j)}$から$x^{(i)}$を学習することも必要になります。

　これを可能にするのが、協調フィルタリング (Collaborative Filtering)です。このモデルは、$\theta \to x \to \theta \to x \to ...$と交互にパラメーターを学習していきます。アルゴリズムは、以下のようになります。

1: パラメーター$x^{(1)}, ..., x^{(n_m)}, \theta^{(1)}, ..., \theta^{(n_u)}$を小さなランダム値に初期化する (Symmetry Breaking)。

2: 目的関数 (Cost Function) $J(x^{(1)}, ..., x^{(n_m)}, \theta^{(1)}, ..., \theta^{(n_u)})$の最小値を満たすパラメーター$x, \theta$を、最急降下法 (Gradient Descent)などを用いて計算する。

　正則化パラメーターを$\lambda$とすると、目的関数$J$は、


J = \frac{1}{2} \sum_{(i,j):r(i,j)=1} ((\theta^{(j)})^{\mathrm{T}}x^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum^{n_m}_{i=1} \sum^{n}_{k=1}(x_k^{(i)})^2
+ \frac{\lambda}{2}\sum^{n_u}_{i=1} \sum^{n}_{k=1}(\theta_k^{(j)})^2

　最急降下法は、


x_k^{(i)} := x_k^{(i)} - \alpha (\sum_{j:r(i,j)=1} ((\theta^{(j)})^{\mathrm{T}} x^{(i)} - y^{(i,j)})\theta^{(j)}_k + \lambda x^{(i)}_k)

\\

\theta_k^{(i)} := \theta_k^{(j)} - \alpha (\sum_{i:r(i,j)=1} ((\theta^{(j)})^{\mathrm{T}} x^{(i)} - y^{(i,j)})x^{(i)}_k + \lambda \theta^{(j)}_k)

3: 学習して得られたパラメーター$\theta, x$を用いて、レビュー$y$を予測する。


y = (\theta^{(j)})^{\mathrm{T}}x^{(i)}

　これで$r(i,j) = 0$で推定された$y$の値が高い映画$i$を、ユーザー$j$にオススメ(Recommend)すればいいわけですね。

まとめのまとめ

異常検知は、正規分布から外れているものを異常値とする。
異常検知のモデル精度は、データが偏っていることが多いので正答率よりもF値を使う。
レコメンダシステムでは、モデルパラメーター$\theta$と商品パラメーター$x$を交互に学習する。

終わりに

　今回は異常検知とレコメンダシステムについてという、実際にデータ解析やビジネスで使える（かもしれない）実践的なアルゴリズムについてでした。こうした実践的なアルゴリズムでも、目的関数を作って、最小値を求めるパラメーターを探して……機械学習の基本を知っていればわかりやすいですね。

　次回は、ビッグデータの機械学習 (Large scale machine learning) を扱います。最近流行りのビッグデータ、面白そうですね。

Coursera Machine Learning (9): 異常検知 (Abnomaly Detection)、レコメンダシステム (Recommender System)

異常検知 (Anomaly Detection)

レコメンダシステム (Recommender System)

まとめのまとめ

終わりに