はじめに
レコメンドシステムでよく用いられる次元削減の手法であるMatrix Factorizationに関してざっくりまとめます。MFは派生アルゴリズムが多かったり損失関数の最適化手法もいくつかあるのですが、今回の記事はMFの概念を理解するために書きました。
協調フィルタリング
まずは協調フィルタリングのおさらいです。協調フィルタリングは複数のユーザーの評価を元に推薦するアイテムを決定するものです。具体的には以下のようなアイテムを推薦します。
①嗜好の似ているユーザーが評価しているアイテム
②過去に高評価をつけたアイテムと似ているアイテム
簡単な例を考えてみます。
(ユーザーベースの協調フィルタリングの場合)
| Movie1 | Movie2 | Movie3 | |
|---|---|---|---|
| User1 | 1 | ? | 5 |
| User2 | ? | ? | 3 |
| User3 | 1 | 3 | 5 |
| User4 | 3 | 3 | 4 |
これは4人のユーザーが3つの映画を評価したデータ(?の箇所は空欄、まだ見ていない映画)です。この時User1のMovie2に対する評価が空欄ですが、User1とUser3を見てみると映画の好みが似ていそうなことが分かります。なのでUser1のMovie2に対する評価は"3"であると予測できます。今は目視で確認しましたが、実際はコサイン類似度やピアソンの相関係数を用いて推薦するべきアイテムを決定します。
なぜ次元削減が必要なのか
ここで本題の次元削減がなぜ必要かということを考えてみます。上で示したような協調フィルタリングではアイテムとユーザーの評価値行列を作成して類似度を計算しますが、実際にサービスとして扱われるデータで作成するとサイズがとても大きくなります。例えば、Amazonではユーザー数が5000万人以上、アイテム数が3億以上あるので計算コストも大きくなります。さらに、それだけユーザーやアイテムを抱えていても各ユーザーが購入、評価するアイテムは限られているので、スパース行列(ほとんど0の行列)になってしまいます。レコメンドでは未評価の場合、ユーザーが興味がなくてスルーしたのか、そもそもアイテムに気付いていないのか区別できないため結果が有効かどうか怪しくなります。
そこで、膨大な全体行列から特徴を取り出して、より小さい行列に近似することで成果を出せるようにします。
Matrix Factorizaion(MF)とは
Matrix Factorizationはレコメンドシステムでよく用いられる低ランク近似の手法です。この手法は、Netflix Prize(Netflixが主催したレコメンドアルゴリズムのコンペ)で結果を残したSimon Funkがはじめに発表したもので、Funk SVDとも呼ばれています。また、MFに関して書いたSimon Funkのブログは今も多くの記事で参照されています。
具体的に見ていきます。
| Movie1 | Movie2 | Movie3 | |
|---|---|---|---|
| User1 | 1 | ? | 5 |
| User2 | ? | ? | 3 |
| User3 | 1 | 3 | 5 |
| User4 | 3 | 3 | 4 |
| (上で使った例) |
レコメンドの目的は、今空欄(?)になっている箇所の評価値を予測し、ユーザーにとってより評価値の高そうな(気に入りそうな)アイテムを推薦することです。
下の図のようにユーザーインデックスu、アイテムインデックスiの評価値行列R(u×i)があるとすると、MFではこれをユーザの特徴を持つ列ベクトルP(u×k)とアイテムの特徴を持つ列ベクトルQ(k×i)に分解します。このときkはi,uよりも小さいです。
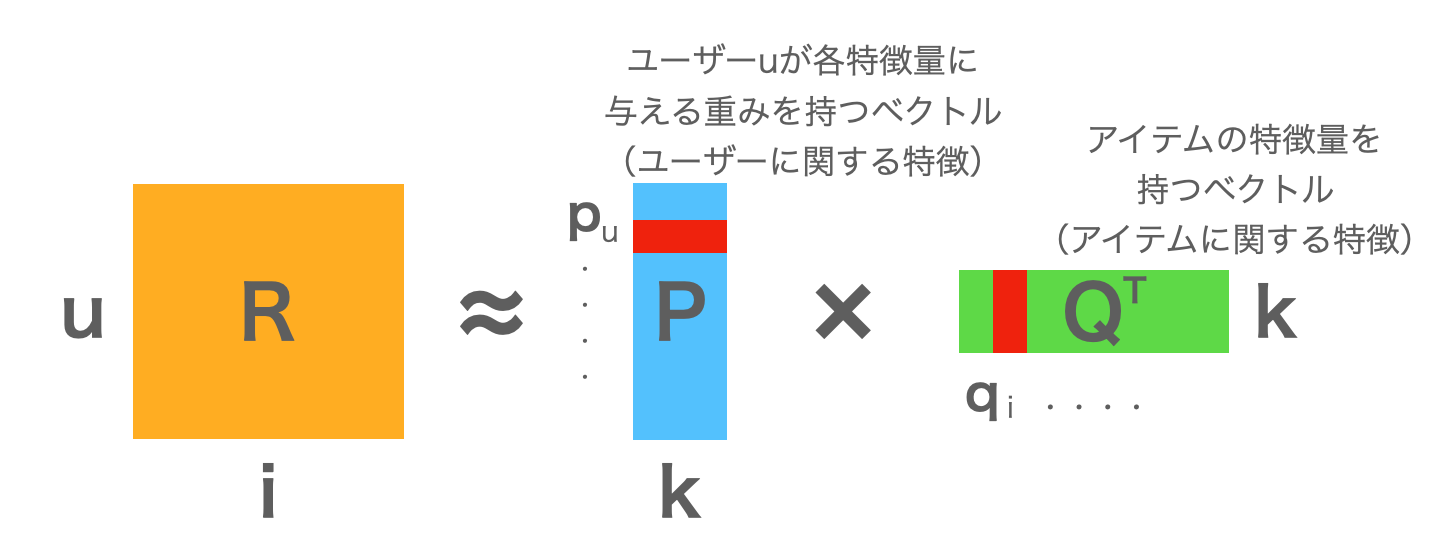
ここで評価の予測値は以下のように表せます。
$$\hat{r_{ui}} = q_{i}^Tp_{u}$$
そして、この予測値が当たるように実際の評価値$r_{ui}$と予測値$\hat{r_{ui}}$の差を小さくしていくという流れになります。オーバーフィッティングを防ぐためにL2正則化項を加えます。
【近似の精度を測定する損失関数】
$$min_{P,Q} \sum_{(u,i) \in R}(r_{ui} - q_{i}^Tp_{u})^2 + \lambda(||q_{i}||^2 + ||p_{u}||^2) (1)$$
この関数を最適化するために以下のような手法が用いられます。
- ALS(交互最小二乗法)
- SGD(確率的勾配降下法)
- WALS(加重交互最小二乗法)
特徴
- 精度がいい
- 計算時間が速い
- モデルの柔軟性が高い
- 並列処理が苦手
最後に
データ数が多くスパースな評価値行列に対しては、このような流れで次元削減を行ってから評価値を予測すると効果的です。今回は基本的なMFに関して書きましたが、バイアス項を加えたものなど派生アルゴリズムがいくつかあるので参照に記載した記事も見てみてください。
参照
Simon Funkのブログ:https://sifter.org/~simon/journal/20061211.html
MF派生アルゴリズムまとめ:https://qiita.com/kondo-k/items/7a67881520da23229ce5