Go to Qiita Advent Calendar 2024 Top
LoginSignup
24
19

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

情報検索・検索エンジンAdvent Calendar 2019Day 15
@kondo-k

Matrix Factorizationの派生アルゴリズムまとめ

Last updated at Posted at 2019-12-14

本記事は情報検索・検索エンジン Advent Calendar 2019の15日目の記事です。
他の人達の記事がすばらしくてずっと胃が痛かったです。温かい目で見てください。
本記事は、ちょっと検索から離れますが情報推薦の分野からの内容になります。

要約

本記事ではMatrix Factorizationの派生手法をいくつかとりあげて紹介します。

具体的には以下の手法を紹介します。下２つは紹介程度に留めます。

  • オリジナルのMatrix Factorization(ベース)
  • ベース+バイアス項
  • ベース+バイアス項+implicit feedback(SVD++)
  • Non-negative Matrix factorization(NMF)
  • regularized single-element-based NMF (RSNMF)
  • ベース+バイアス項+implicit feedback+時系列処理(timeSVD++)
  • ベース+バイアス項+implicit feedback+Confidence level

背景

Matrix Factorization(MF)はいわずとしれた推薦システムにおいて重要な手法です。
MFについての解説は他にすばらしい記事があるのでよく知らない人は一読してみてください。

##オリジナルMF

オリジナルの手法はNetFlix Prize優勝者のブログにあります。

先ほど紹介したMatrix FactorizationとはやMatrix Factorizationとレコメンドと私でもこのオリジナルの手法が解説されています。
いま一度確認しておくと、ユーザーインデックスを$u$, アイテムインデックスを$i$としてユーザー$u$のアイテム$i$への評価$r_{ui}$を(1)の式で予測することを考えます(詳細は上の記事を参考にしてください)。ここでは$q_i, p_u$はそれぞれアイテム、ユーザーを表す$k$次元のベクトルですう。

$$
\hat{r}_{ui}=q_i^Tp_u\qquad(1)
$$

予測値$\hat{r}_{ui}$がよく当たるように$q_i,p_u$を学習していくわけですが、その目的関数が下の(2)式になります。直感的には、正解値と予測値の差を小さくするような関数にノルム正則化項を加えたものになります。$(u,i)\in K$はユーザーとアイテムのセット(u,i)が既知として存在するもののみを用いるということを表しています。

目的関数
$$
min_{P,Q}\sum_{(u,i)\in K}(r_{ui}-q_i^Tp_u)^2+\lambda(||q_i||^2+||p_u||^2)\qquad(2)
$$

この目的関数の最適解を導くためのアルゴリズムとしてSGDやALSが用いられます。
SGDの場合、目的関数を微分して更新式を導くと(3)式のようになります

更新式

\begin{align}
&e_{ui}=r_{ui}-\hat{r}_{ui}\\
&q_i = q_i+\gamma(e_{ui}p_u-\lambda q_i)\qquad(3)\\
&p_u = p_u+\gamma(e_{ui}q_i-\lambda p_u)
\end{align}

並列計算したい場合や行列がスパースでない場合はALSを使うこともありますが基本的にはSGDのほうが計算が早くて扱いやすいです。$\gamma$や$\lambda$を$q_i$と$p_u$で変えることもできます。

ちなみにバイスのないこのアルゴリズムがProbabilistic Matrix Factorizationとよばれる手法と同じらしいです。詳細確認していませんが論文だけ載せておきます。
Ruslan Salakhutdinov and Andriy Mnih. Probabilistic matrix factorization. 2008.

ベース+バイアス項

次に、上のオリジナルの手法にバイアス項を加えたものを紹介します。

なぜバイアス項を加える必要があるかを簡単に説明すると、
例えば、ある商品が高評価をつけられやすかったり、あるユーザーが高評価をつけやすかったりする傾向がある時に$\hat{r}_{ui}=q_i^Tp_u$だけでは説明できない場合があります。そのために各商品とユーザーにバイアスを設定することでその部分を学習させることができるわけです。

バイアス項は全評価値の平均$\mu$と各アイテム、各ユーザーのバイアス$b_i,b_u$からなっており、バイアス項を加えた予測評価値は以下の(4)式で表されます。
$$
\hat{r}_{ui}=\mu+b_i+b_u+q_i^Tp_u\qquad(4)
$$
目的関数、更新式もそれに応じて以下の(5),(6)式になります。

目的関数
$$
min_{P,Q}\sum_{(u,i)\in K}(r_{ui}-\mu-b_i-b_u-q_i^Tp_u)^2+\lambda(||q_i||^2+||p_u||^2+b_u^2+b_i^2)\qquad(5)
$$

更新式

\begin{align}
&e_{ui}=r_{ui}-\hat{r}_{ui}\\
&b_i=b_i+\gamma(e_{ui}-\lambda b_i)\\
&b_u=b_u+\gamma(e_{ui}-\lambda b_u)\qquad(6)\\
&q_i = q_i+\gamma(e_{ui}p_u-\lambda q_i)\\
&p_u = p_u+\gamma(e_{ui}q_i-\lambda p_u)
\end{align}

ベース+バイアス項+implicit feedback(SVD++)

おそらくオリジナルの論文は下のものです。

Yehuda Koren. Factorization meets the neighborhood: a multifaceted collaborative filtering model. 2008.

SVD++は評価行列だけではなくてその他のimplicitな情報をモデルに与える手法です。

この手法は推薦システムにつきものであるコールドスタート問題を解決するというモチベーションで開発されました。MFでスパースな行列が扱えるといっても、すでにあるデータからしか学習できない以上、評価値データがあまりない最初の段階では適切な推薦が行なえません。そこでimplicitな情報、例えば過去の購買履歴であったり閲覧履歴であったりといった情報を与えることでその問題を緩和できるということです。

具体的には、あるユーザー$u$がimplicitな評価値を与えているアイテム群を$I_u$とします。そして、(k次元)×(アイテム数)のimplicitなアイテム行列$X$から$I_u$に含まれるアイテムのベクトルだけを足し合わせたもの$\sum_{j\in I_u}x_j$を考えます。k次元ベクトル$x_j$を足し合わせているのでその和もk次元ベクトルとなります。

少しわかりにくいので補足すると$x_j$自体はアイテムの情報を表すベクトルですが、それをユーザーに関連付けた$I_u$に含まれる分だけ足し合わせているので、$\sum_{j\in I_u}x_j$はユーザーの情報を表すベクトルになります。これを正規化して$p_u$に足すことでimplicitなデータを加えられます($\sum_{j\in I_u}x_j$はユーザーを表すベクトルなので当然足すのは$p_u$)。

よって予測評価値以下の(7)式になります。

$$
\hat{r}_{ui}=\mu+b_i+b_u+q_i^T(p_u+|I_u|^{-1/2}\sum_{j\in I_u}x_j)\qquad(7)
$$

また、アイテムへの評価値としてユーザー情報を加えるのではなく、ユーザーの属性情報(性別や年齢等)をそのまま加えることもできます。同様にユーザー$u$が含まれる属性群を$A_u$, その情報を$y_a$とすると属性情報は$\sum_{a\in A_u}y_a$となり、これを$p_u$に足すことで予測評価値(8)式を得ます。
$$
\hat{r}_{ui}=\mu+b_i+b_u+q_i^T(p_u+|I_u|^{-1/2}\sum_{j\in I_u}x_j+\sum_{a\in A_u}y_a)\qquad(8)
$$

Non-negative Matrix factorization(NMF)

NMFはその名の通りすべての値が非負となるように学習・予測していくアルゴリズムです。だいたい評価値というのは非負である場合が多いため、それに準じて学習するアルゴリズムを開発するのは当然のモチベーションと言えます。

オリジナルの論文は下の論文で、最初は推薦システムの分野ではなく画像生成の分野で生まれました。そもそもこの頃は"Matrix Factorization"という単語は推薦分野では使われていなかったらしいです。最初に紹介したオリジナルのブログが出てから、呼び方が変わっていき、次第にそう呼ばれるようになっていったらしいのですが、この画像生成分野ではすでに1999年からこの単語を使っていますね。

※NMFの原型は1994年の論文にあったらしいのですが、あまり詳しく掘り下げません

Daniel D.Lee and H. Sebastian Seung. Learning the parts of objects by non-negative matrix factorization. 1999

それでは、どのようにしてすべての値を非負となるように学習するのかを見ていきます。

この手法のキモは学習率の調整にあります。

原理的に言って、「最初の値が全て非負」で「更新式に引き算がない」という条件を満たせばすべての値が非負になるように学習されます。そこで、そうなるように学習率$\gamma$を調整します。

更新式(3)を例にします。考え方の理解のためなので厳密な計算ではないですし、オリジナルのNMF手法とも全く異なります。

\begin{align}
&e_{ui}=r_{ui}-\hat{r}_{ui}\\
&q_i = q_i+\gamma(e_{ui}p_u-\lambda q_i)\qquad(3)\\
&p_u = p_u+\gamma(e_{ui}q_i-\lambda p_u)
\end{align}

真ん中の式だけ考えてみます。まず代入・展開を行います。

\begin{align}
q_i&=q_i+\gamma r_{ui}p_u-\gamma\hat{r}_{ui}p_u-\gamma\lambda q_i\\
&=q_i+\gamma r_{ui}p_u-\gamma(\hat{r}_{ui}p_u+\lambda q_i)\\
\end{align}

この更新式から引き算をなくしたいので、

$$
\gamma=\frac{q_i}{\hat{r}_{ui}p_u+\lambda q_i}
$$

とすると、以下の(9)式のようになり、更新式から引き算が消えます。$p_u$も同様です。
$$
q_i=q_i\frac{p_ur_{ui}}{\hat{r}_{ui}p_u+\lambda q_i}\qquad(9)
$$

regularized single-element-based NMF (RSNMF)

以下の論文を参考にしてみてください。特殊な権限がないと見れないかもしれませんが。

Xin Luo, Mengchu Zhou, Yunni Xia, Qingsheng Zhu. An Efficient Non-Negative Matrix-Factorization-Based Approach to Collaborative Filtering for Recommender Systems. 2014

オリジナルのNMFとの違いは以下の２点です。

  • single-element-based
  • Tikhonov(チコノフ) 正則化

single-element-based

オリジナルのNMFは画像生成分野で生まれたため、データのスパーシティを考慮されていませんでした。そのため、推薦分野でそのまま使ってもうまくいかないので改良が必要です。つまり、オリジナルでは行列のすべての要素を対象に更新式を構築していたものを、データのあるものに限定して更新式を組み直す必要があります。

Tikhonov(チコノフ) 正則化

これは今まで見てきたノルム正則化項($||q_i||^2$)のようなものです。これを入れることで、計算効率を落とすことなく精度を上げることに成功しました。

更新式

p_u=p_u\frac{\sum_{i\in I_u}q_ir_{ui}}{\sum_{i\in I_u}q_i\hat{r}_{ui}+\lambda_u|I_u|p_u}\\
q_i=q_i\frac{\sum_{u\in U_i}p_pr_{ui}}{\sum_{u\in U_i}p_u\hat{r}_{ui}+\lambda_i|U_i|q_i}

ベンチマーク

ここまでいくつかアルゴリズムを見てきて、じゃあいったいこの中でどれが良いのと思われた方もいるかもしれません。
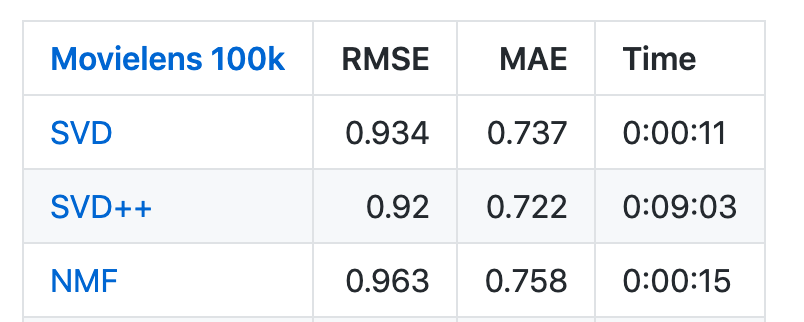
SurpriseというMatrix Factorization向けのライブラリにMovieLensのデータを使ってのベンチマークがあります。SVDというのがバイアス項を加えたMFで、NMFがRSNMFの結果です。SVD++が１番精度が良いのですが、計算時間が非常に長いのが分かるかと思います。

スクリーンショット 2019-12-14 20.19.13.png スクリーンショット 2019-12-14 20.19.47.png

###ベース+バイアス項+implicit feeadback+時系列処理(timeSVD++)

ここから２つの手法はあまり詳細に触れません。知りたい方は論文を参照してください。今後詳細に解説する記事がかけたら載せたいです。

オリジナルの論文

Yehuda Koren. Collaborative Filtering with Temporal Dynamics. 2009

この手法はユーザーの好みとかアイテムの評価とかって時間によって変わるよねという当たり前かつ重要な考えが基になっています。最近ではDeepな時系列モデルがそのへんを優秀に解いているらしいですが...。

最初に、どの変数が時間によって変化するかを考えます。

  • $b_i$はアイテムの評価される傾向(高評価されやすい等)を表しているので、これは時間によって変わります

  • $b_u$はユーザーの評価する傾向(高評価しやすい等)を表しているので、これは時間によって変わります

  • $p_u$はユーザーアイテム間の相互作用におけるユーザーの好みを表しているので、これは時間によって変わります

  • $q_i$はアイテムの性質を表しているので、これは時間によって変わりません

よって、導かれる結論として、予測評価値は(10)式で表されます
$$
\hat{r}_{ui}=\mu+b_i(t)+b_u(t)+q_i^Tp_u(t)\qquad(10)
$$

これらを時間の関数としてどう表していくのかという問題に移ります。

アイテムバイアス$b_i$

まず、アイテムバイアス$b_i$はそれほど短期間で変わらないと考えられるため、単純にある程度の期間で分割してその平均を考慮すればよいとします。実際の予測ケース想定すると、レコメンドするそのタイミングから過去n日の平均を取るみたいなことなのかなと思います。式にすると(11)式のようになります。
$$
b_i(t)=b_i + b_{i,Bin(t)}\qquad(11)
$$

ユーザーバイアス$b_u$, ユーザーの好み$p_u$

次に、ユーザーバイアス$b_u$は短期間で変化することがあるため少し工夫します。手法が3つ紹介されていて、実験的にはスプライン補間+single day effectが最も良い精度が出ています。

  • 単純な線形補間
    • $b_u(t)=b_u+|ある基準時間から今までの時間間隔|^\beta×\alpha_u$として$b_u, \alpha_u$を学習していきます
  • スプライン補間
    • スプラインによる補間
    • $b_u(t)=b_U+\frac{\sum_l e^{-\gamma |t-t_l|}b_{t_l^u}^u}{\sum_l e^{-\gamma |t-t_l|}}$
  • Single day effect
    • その日限りの爆発的な傾向というのを考慮するため、上の補間に加えてあるユーザーのその日のみのバイアス$b_{u,t}$を加えます

ユーザーの好み$p_u$も$b_u$と同じで補間+single day effectで時間の関数化をしています。

実験結果を見ると、従来手法と比べてかなり良い結果が出ています

image-20191213130357976.png

ベース+バイアス項+implicit feedback+Confidence level

オリジナル論文

Yifan Hu, Yehuda Koren, Chris Volinsky, Collaborative Filtering for Implicit Feedback Datasets, 2008.

すべての評価情報が等価ではないという考えのもと開発された手法です。

ユーザーの行動傾向等からデータごとにConfidence levelを測るConfidence functionを学習します。
そのConfidence levelに合わせてデータを重み付けするような形で学習を進めていくことで、データの重要度を考慮したモデルが作成できるという発想です。

最後に

オリジナルのMatrix Factorizationを解説したものは多いのですが、その派生形をとりあげたものがあまりなかったので今回まとめてみました。

近年はDeepなモデルでの推薦がもっぱら研究対象ですが、RecSys2019のBest Paperでも取り上げられたようにDeepなモデルばかりが優れているとは限らないのでこのへんのアルゴリズムもおさえておきたいです。

このへんの実装もおいおい書きます。

Reference

Ruslan Salakhutdinov and Andriy Mnih. Probabilistic matrix factorization. 2008.

Yehuda Koren. Factorization meets the neighborhood: a multifaceted collaborative filtering model. 2008.

Daniel D.Lee and H. Sebastian Seung. Learning the parts of objects by non-negative matrix factorization. 1999

Xin Luo, Mengchu Zhou, Yunni Xia, Qingsheng Zhu. An Efficient Non-Negative Matrix-Factorization-Based Approach to Collaborative Filtering for Recommender Systems. 2014

Yehuda Koren. Collaborative Filtering with Temporal Dynamics. 2009

Yifan Hu, Yehuda Koren, Chris Volinsky, Collaborative Filtering for Implicit Feedback Datasets, 2008.

SVD++, time SVD++, ConfidenceSVDを開発したYehuda Koren氏のまとめ記事↓
https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf

24
19
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
24
19

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?