レコメンドにおける次元削減手法の一つであるMatrix Factorizationについてまとめた自分用メモ的なものです。
なおタイトルは「部屋とYシャツと私」にちなんだだけで、ちなんだ意味はありません。
1. レコメンドシステムにおける次元削減
1.1 レコメンドの設定と協調フィルタリング
すでにレコメンドをたくさんされている方にとってはとても当たり前の話かもしれませんが一応前提をば。
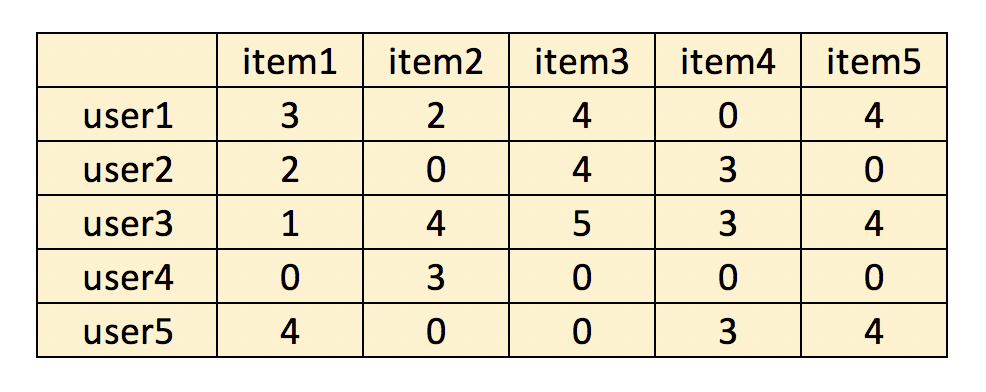
今回考えるデータセットはMovieLens100kのように「ユーザ×アイテム」の行列でできているもので、例えば以下のような形のものを想定しています。
レコメンドでおなじみの協調フィルタリング1では相関係数やコサイン類似度を用いてユーザ(orアイテム)同士の類似度を出し、それを用いた評価の予測値に基づきレコメンドをするという趣旨のものでした。
この協調フィルタリングのようなレコメンド手法のことを近傍ベースアルゴリズム(Neighborhood-based Algorithm)やメモリベースアルゴリズム(memory-based Algorithm)なんていったりもします。
1.2 近傍ベース手法(協調フィルタ)の課題
協調フィルタ自体は今でもまだまだ使われている手法ではありますが、全く課題がないというわけではありません。
たとえば[2]の文献ではその課題が以下のようにまとめられています。
-
sparsity
例えばユーザベース協調フィルタの場合類似度を計算する対象になるユーザ同士は最低でも2つの共有のアイテムを評価している必要があります。
しかしながらAmazonやYouTubeのようにユーザ数もアイテム数も多い場合ほとんどのユーザが評価したアイテムは全アイテムのうちのほんのわずかな割合で、ユーザによっては「共通して評価したアイテム」がかなり少なくなってしまいます(reduced coverage)。
またそのようにあまり評価をしていないユーザが多く含まれてしまう場合レコメンドの精度にも悪影響が出てしまうと言われています。 -
scalability
データが大きくなればなるほど計算量が多くなりマシンパワーが求められます。
例えばAmazonや楽天のようなECサイトの場合ユーザ数とアイテム数がかなり膨大で、単純にその大きさの行列を持つだけでもかなりのメモリを消費してしまいます。
(ex. 大抵のマシンでは10万×10万のndarrayを作るだけでかなりきついと思います) -
synonymy
似たような性質をもつ違う名前のアイテム同士が別のものとして捉えられてしまうという問題です。
例えば赤い缶のコーラを買う人と青い缶のコーラを買う人はそれぞれ別の色のコーラを買わないと思われますが、趣向自体は似たようなものだと考えられます。
しかしながら通常の協調フィルタではこの赤い缶ユーザと青い缶ユーザの類似性をうまく捉えることができません。
1.3 レコメンドと次元削減
上記のような問題に対処するためここでは次元削減を行うこととします。
といっても今回行う次元削減は通常の機械学習にて行うような類のものではなく、抽出した行列たちから元の行列を推定できるような次元削減を行います(なにか違うだろうか)。
次元削減を行うことで潜在因子(latent factor)を抽出し、さらにそれに基づいてもとの行列を近似できるという利点が存在しています。
(特にfully-ranked low rank approximationの場合)もとの行列に欠損値が存在していても頑健に近似行列を推定することもできます。
今回扱うのは行列分解(Matrix Factorization)と呼ばれるものですが、通常レコメンドの文脈で「行列分解」というと特異値分解(Singular Value Decomposition)をさすことが多い(らしい)です。
ですがここではあくまで特異値などを用いないUnconstrained Matrix Factorizationについて扱っていきます。
2. Matrix Factorizationの考え方
2.1基本アプローチ
ユーザ数(行数)$m$、アイテム数(列数)$n$で構成されるランク$k << min ( m, n)$の評価値行列$R$を考えます。
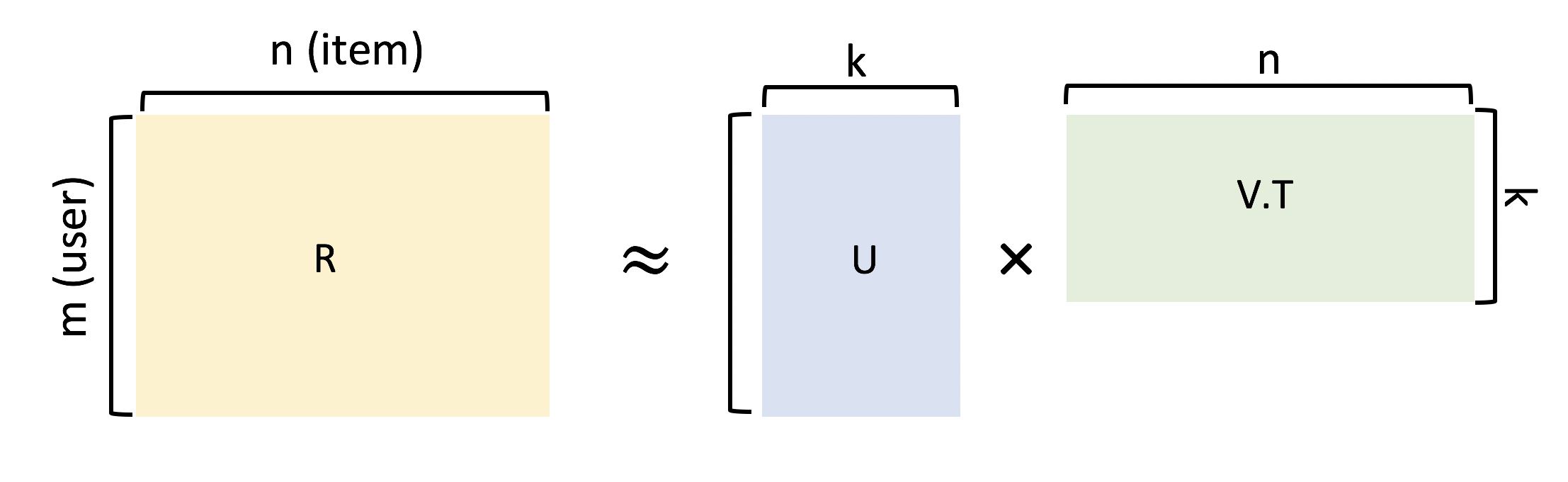
Matrix Factorizationではこの評価値行列$R$を以下のような2つの行列$U$と$V$で近似していきます(なお $U = m \times k$の行列、$V = n \times k$ の行列とします)。
R \approx U V^T
図解するとこんなイメージです
一見すると$U$や$V$のそれぞれの値はユーザとアイテムの相関を表しているようにも見えますが、それらは単なる潜在因子であり解釈できるかどうかは定かではありません。
Matrix Factorizationでやっていくのはこの$U$と$V$で近似した行列のlossを減らしていくことです。
Minimize \, J \approx \frac{1}{2} || R - UV^T||^2 \\
subject \, to: \, No \, constraints \, on \, U \, and \, V
この定式化は元々の評価値行列$R$に欠損値がない場合にはそのまま使えるものの、実際の評価値行列には多く欠損値が含まれているためこのままではうまくいきません。
そこで実際に観測されたユーザ・アイテムのペア$(i, j) \in S$の評価値$r_{ij}$のみを用いてこの定式化を書き換えていきます。
推定したい評価値行列$\hat{R}$のある特定のユーザ$i$・アイテム$j$の予測評価値$\hat{r_{ij}}$を以下のように表します。
\hat{r_{ij}} = \sum_{s=1}^k u_{is} \cdot v_{js} \\
where \, U = [u_{is}]_{m \times k}, \, V = [v_{is}]_{n \times k}
$U$と$V$はそれぞれユーザ$i$に関するdenseな行列:とアイテム$j$に関するdenseな行列です。
これを用いて最小化したい目的関数を以下のように書き換えます。
Minimize \, J = \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - \sum_{s=1}^k u_{is} \cdot v_{js})^2\\
subject \, to: \, No \, constraints \, on \, U \, and \, V
この中の$r_{ij} - \sum_{s=1}^k u_{is} \cdot v_{js} = r_{ij} - \hat{r_{ij}}$がいわゆる予測誤差に当たる部分です。
行列$U$と$V$の更新はおなじみstochastic Gradient Descentで行なっていきます。
$J$をそれぞれの行列の要素$u_{iq}$と$v_{jq}$について微分して得られる
\frac{\partial J}{\partial u_{iq}} = \sum_{j:(i,j) \in S} (r_{ij} - \sum_{s=1}^k u_{is} \cdot v_{is})(-v_{jq}) \, \forall i\in \{1...m\}, q \in \{1..k\} \\
\frac{\partial J}{\partial v_{iq}} = \sum_{i:(i,j) \in S} (r_{ij} - \sum_{s=1}^k u_{is} \cdot v_{is})(-u_{iq}) \, \forall j \in \{1...n\}, q \in \{1..k\}
を用いて
u_{iq} <= u_{iq} - \alpha \cdot \Bigl[ \frac{\partial J}{\partial u_{iq}} \Bigr] \, \forall q \in \{ 1...k \} \\
v_{iq} <= u_{iq} - \alpha \cdot \Bigl[ \frac{\partial J}{\partial v_{iq}} \Bigr] \, \forall q \in \{ 1...k \}
と示されます。
2.2 正則化項を加える
いつもの機械学習同様過学習を避けるための正則化項を加えることもできます。
目的関数は正則化パラメータ$\lambda$を用いて
Minimize \, J = \frac{1}{2}_{(i,j) \in S}\Bigl(r_{ij} - \sum_{s=1}^k u_{is} \cdot v_{js} \Bigr)^2 + \frac{\lambda}{2}\sum_{i=1}^m\sum_{s=1}^k u_{ij}^2 + \frac{\lambda}{2}\sum_{j=1}^n\sum_{s=1}^k v_{ij}^2
それぞれの変数で微分した式は以下のように書き換えられます。
\frac{\partial J}{\partial u_{iq}} = \sum_{j:(i,j) \in S} (r_{ij} - \sum_{s=1}^k u_{is} \cdot v_{is})(-v_{jq}) + \lambda u_{iq} \, \forall i\in \{1...m\}, q \in \{1..k\} \\
\frac{\partial J}{\partial v_{iq}} = \sum_{i:(i,j) \in S} (r_{ij} - \sum_{s=1}^k u_{is} \cdot v_{is})(-u_{iq}) + \lambda v_{jq} \, \forall j \in \{1...n\}, q \in \{1..k\} \\
更新式は先ほどと同じです($\frac{\partial J}{\partial u_{iq}}$の中身が違うだけなので)。
3. 実装
3.1 とりあえず実装
まず$U$,$V$の更新は以下のように書かれます。
# R...m-n rating matrix
# U...m-k dense matrix
# V...k-n dense matrix
# X...list of user_id
# Y...list of item_id
for i in X:
for j in Y:
r_ij = R[i-1,j-1]
if r_ij > 0:
err_ij = r_ij - np.dot(U[i-1,:], V[:,j-1])
in range(k):
U[i-1,q] += alpha * (err_ij * V[q, j-i] + lamda * U[i-1, q])
V[q, j-1] += alpha * (err_ij * U[i-1, q] + lamda * V[q, j-i])
これで$U$と$V$が更新されたのでいよいよ誤差を計算していきます。
# approximation
R_hat = np.dot(U, V)
# calculate estimation error for observed values
for i in X:
for j in Y:
r_ij = R[i-1, j-1]
r_hat_ij = R_hat[i-1, j-1]
if r_ij > 0:
error += pow(r_ij - r_hat_ij,2)
# regularization
error += (lamda * np.power(U,2).sum()) / 2
error += (lamda * np.power(V,2).sum()) / 2
あとはここで算出したerrorが収束するor目的のiteration数終わるまでこれを繰り返すだけです。
全体像を示すとこのようになります。
import numpy as np
from scipy import sparse
class MatrixFactorization():
def __init__(self, R, X, Y, k, steps=200, alpha=0.01, lamda=0.001, threshold=0.001):
self.R = R
self.m = R.shape[0]
self.n = R.shape[1]
self.k = k
# initializa U and V
self.U = np.random.rand(self.m, self.k)
self.V = np.random.rand(self.k, self.n)
self.alpha = alpha
self.lamda = lamda
self.threshold = threshold
self.steps = 200
# preserve user_id list and item_id list
self.X = X
self.Y = Y
def shuffle_in_unison_scary(self, a, b):
rng_state = np.random.get_state()
np.random.shuffle(a)
np.random.set_state(rng_state)
np.random.shuffle(b)
def fit(self):
for step in range(self.steps):
error = 0
# shuffle the order of the entry
self.shuffle_in_unison_scary(self.X,self.Y)
# update U and V
for i in self.X:
for j in self.Y:
r_ij = self.R[i-1,j-1]
if r_ij > 0:
err_ij = r_ij - np.dot(self.U[i-1,:], self.V[:,j-1])
for q in range(self.k):
self.U[i-1,q] += self.alpha * (err_ij * self.V[q, j-i] + self.lamda * self.U[i-1, q])
self.V[q, j-1] += self.alpha * (err_ij * self.U[i-1, q] + self.lamda * self.V[q, j-i])
# approximation
R_hat = np.dot(self.U, self.V)
# calculate estimation error for observed values
for i in self.X:
for j in self.Y:
r_ij = self.R[i-1, j-1]
r_hat_ij = R_hat[i-1, j-1]
if r_ij > 0:
error += pow(r_ij - r_hat_ij,2)
# regularization
error += (self.lamda * np.power(self.U,2).sum()) / 2
error += (self.lamda * np.power(self.V,2).sum()) / 2
if error < self.threshold:
break
return self.U, self.V
これで完成です。
なおこれを作成するに当たって[4]と[5]をかなり参考にしました。先人の知恵はありがたい…!
3.2 試しに実験
ひとまずできたので簡単なサンプルで試してみたいと思います。
まずはサンプルの作成から。
なおここでは僕の好みで$R$をsparseにしていますが普通のndarrayでも問題なく実行できます。
# R = np.random.randint(6, size=(5, 8), dtype=np.int8)
R = sparse.csr_matrix(np.random.randint(6, size=(5, 8)), dtype=np.int8)
X = np.arange(1, 6) # mock for user_id
Y = np.arange(1, 9) # mock for item_id
R.toarray()
array([[0, 3, 3, 2, 5, 5, 5, 0],
[1, 1, 5, 3, 2, 1, 1, 5],
[3, 5, 0, 3, 3, 5, 4, 0],
[2, 1, 2, 1, 0, 1, 1, 4],
[4, 1, 0, 1, 4, 5, 2, 5]], dtype=int8)
実行してみます。
mf = MatrixFactorization(R, X, Y, k=2, steps=200)
U, V = mf.fit()
print(np.dot(U,V))
[[[3.68850624 3.12706952 3.84084925 2.29584398 4.33233016 4.99289072
3.99137391 8.11477969]
[0.78776418 1.78582684 4.17229366 2.67923648 1.59270195 1.76097037
1.60911958 4.83868345]
[3.99292889 3.48192533 4.4479895 2.67479537 4.74766169 5.46509373
4.38628958 9.05333077]
[2.48407518 1.37378371 0.39137586 0.11260257 2.48054911 2.90760486
2.19248438 3.43108926]
[2.73049401 2.09851214 2.19454047 1.27591607 3.07792608 3.56165751
2.80825566 5.40609505]]
ひとまずもともと値の入っていなかったところにきちんと予測値が入っているのが確認できました。
ただもともと値が入っていたところの予測値がちょっとずれてるなと感じるところもあり結果は微妙に気になるところです。
3.3 MovieLens100kで精度確認
以前の記事と同じような感じでMovieLensを用いたレコメンドとその精度を出してみました。
その記事とここまでやったことの繰り返しになってしまうのでここでは結果だけを示します。
具体的なコード全体はこちらのColaboratoryにありますので気になる方は参照してみてください。
k = 20
steps = 100
Precision: 0.05121951219512226
うーん前回の協調フィルタがPrecision=0.15だったのに比べてかなり低いですね。
もう少しパラメータのチューニングをしたら結果が変わるのかもしれませんがちょっとそこまで試す余裕が…ないわけではないのでいつかやろうと思います(学習にかかる時間が10 sec / stepとちょっとかかるため)
ということで今回はここまでです。
お粗末様でした。
参考資料 / リンク
今回の記事のうち知識的側面は[1]と[2]を、実装に関する面は[4]と[5]からかなり参考にしました。
[1] Charu C. Aggrawal, Recommender Systems: The Textbook, Springer, 2016
[2] Badrul M. Sarwar, George Karypis, Joseph A. Konstan, John T. Ried, Application of Dimensionality Reduction in Recommender System -- A Case Study , WebKDD Workshop at ACM SIGKDD Conference, 2000
[3] Matrix Factorization and Neighbor Based Algorithms forthe Netflix Prize Problem
[4] Matrix Factorization: A Simple Tutorial and Implementation in Python
[5] Matrix Factorizationとは - Qiita