EchoStateNetworkをtf.kerasで書いてみた

深層学習以外の機械学習と応用技術 by QuantumCore Advent Calendar 2019では「Qore」APIを使った記事がほとんどですが、

②リザーバコンピューティングについてや深層学習以外の機械学習アルゴリズムについての紹介記事

でもOKとのことで、本記事ではリザーバコンピューティングの根幹技術である**EchoStateNetwork(ESN)**を解説しながらtensorflow(-keras)で実装します。

「Qore」APIは自体は高性能なようで非常に興味はありますが、やはり得体の知れないもの（愚生視点）を使うのは不安なので、自分でスクラッチ実装してみることで基本の理解を試みます。ちなみに、すでにgithubにはESNの実装がごまんとupされており、tensorflowによる実装も何番煎じが分かりませんが、ただtf.kerasでの実装はまだないかと思います。多分。

#ESNCellの解説と実装
ESNはRNNの1種でもあるため、 tf.keras.layers.RNNにESN用のCellを投げることで容易に実装出来ます。
そこで、Cellの部分の実装の紹介と簡単に解説したいと思います。
最初に、ESNCellのコードはこちら。

class ESNCell(tf.keras.layers.Layer):
    """
    ESN single cell for "tf.keras.layers.RNN".
    """
    
    def __init__(self, units, sr_scale=1.0, density=0.2, leaking_rate=0.9, **kwargs):
        
        def _W_initializer(shape, dtype=None, partition_info=None):
            w_init = tf.random.normal(shape, dtype=dtype)
            mask = tf.cast(tf.math.less_equal(tf.random.uniform(shape), self._density), dtype) #sparse 0-1 matrix
            w_init_sparse = w_init * mask
            Eigenvalues_w_init, Eigenvectors_w_init = tf.linalg.eigh(w_init_sparse)
            Spectral_radius = tf.math.reduce_max(tf.abs(Eigenvalues_w_init))
            w_init_sparse_r = w_init_sparse * self._sr_scale / Spectral_radius #normalization based on Spectral_radius
            return w_init_sparse_r
        
        self.state_size = units
        self._sr_scale = sr_scale
        self._density = density
        self._leaking_rate = leaking_rate
        self._W_initializer = _W_initializer
        super(ESNCell, self).__init__(**kwargs)
    
    def build(self, input_shape):
        self.W_in = self.add_weight(shape= (input_shape[-1], self.state_size),
                                    initializer=tf.random_normal_initializer,
                                    trainable = False,
                                    name='W_in')
        self.W = self.add_weight(shape=(self.state_size, self.state_size),
                                 initializer=self._W_initializer,
                                 trainable = False,
                                 name='W')
        self.b = self.add_weight(shape=(self.state_size,),
                                 initializer=tf.random_normal_initializer,
                                 trainable = False,
                                 name='Bias')
        self.built = True

    def call(self, inputs, states):
        x_n_1 = states[0]
        x_tilda_n = tf.math.tanh(tf.tensordot(inputs, self.W_in, axes=1) + tf.tensordot(x_n_1, self.W, axes=1) + self.b)
        x_n = (1 - self._leaking_rate) * x_n_1 + self._leaking_rate * x_tilda_n
        return x_n, [x_n]

RNNが分かっている前提でお話します。
ESNのセルが持つ重みはRNNと同様、入力用の重み$W_{in}$と、状態の重み$W$およびバイアス$b$です。
tf.kerasではまずdef build(self, input_shape):の部分でこれらを定義します。
ここで重要なのが

1. 重みは初期化の後はずっと固定で、学習はされない
2. 状態重み$W$はSpectralRadiusが1以下のスパースな行列(ただし経験的に1以上でも機能する)

の2点です。
前者の方はtrainable = FalseすればOKです。
後者を満たすため、_W_initializerを自作しています。

_W_initializerでは、まずランダムな行列w_initを作り、密度がdensityな0-1スパース行列maskを作ります。それらをドット積でかけることで、スパースな行列w_init_sparseが完成します。さらに、これのSpectralRadiusを求めます。SpectralRadiusは「固有値の絶対値の最大値」で求まります。最後にw_init_sparseをSpectralRadiusで割れば、SpectralRadiusが1のランダムスパース行列の完成です。もちろんここから任意の値sr_scaleをかけてやれば、SpectralRadiusがsr_scaleとなるランダムスパース行列が出来ます。

最後に、RNNの計算の部分def call(self, inputs, states):です。ここでは、次の式に基づいて計算しています。

時刻$n$のときの状態ベクトルを$x(n)$とし、入力を$u(n)$とすると、状態ベクトルの更新式は

$\tilde{x}(n) = tanh(W_{in}u(n) + Wx(n-1) + b)\tag{1}$
$x(n) = (1-\alpha)x(n-1)+\alpha\tilde{x}(n)\tag{2}$

$\alpha$は漏れ率です。特に気にせず1でもなんでもいいです。
計算後、RNN同様状態ベクトルが出力および次の時刻のセルへ渡されます。

以上が実装の解説です。前述した通り、上記のコードでクラスを定義したらtf.keras.layers.RNNにESN用のCellを渡すだけです。あとはRNNと同じです。

例えば、単純な回帰問題の場合は

$y(n) = W_{out}x(n) + b_{out}\tag{3}$

esn_cell = ESNCell()
x_n = tf.keras.layers.RNN(esn_cell)(u_n)
y = tf.keras.layers.Dense(1)(x_n)

こんな感じです。

#学習について
式(3)の回帰問題を考えます。
ESNCell内の重みは学習されないので、$W_{out}$のみを更新すればよいことになります。
すると、学習は単なる線形回帰問題です。
バッチ学習であれば線形回帰、リッジ回帰。
オンラインで学習する場合はオンライン用の線形回帰(LMSなど)です。
また、線形回帰問題なので学習は爆速です。

#動作確認
上記の回帰問題をESNで解くものをscikit-learn風のクラスで実装しました。
学習はTikhonov正則化(リッジ回帰)で実装してます。
コードはこちらです。
以下、そこのexample.ipynbの内容となります。

では早速動かしてみましょう。
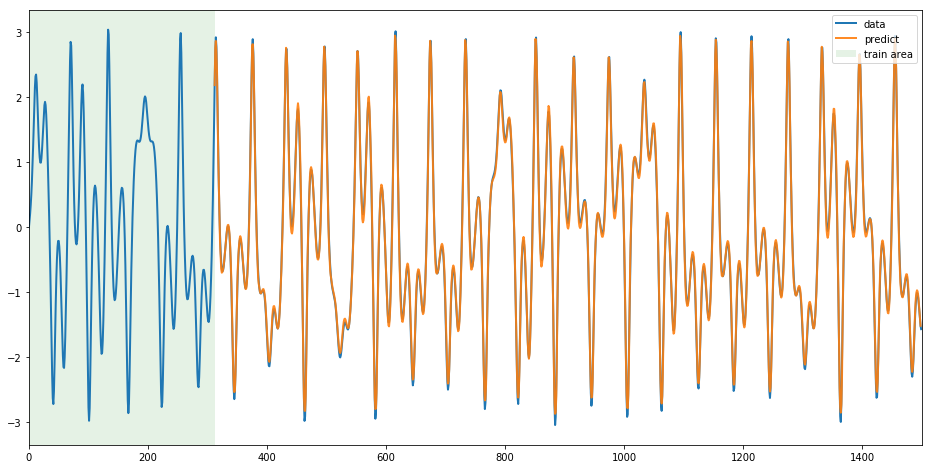
下図のようなカオス単変量時系列データにおいて、16点の部分時系列から次の1点を予測する問題を考えます。

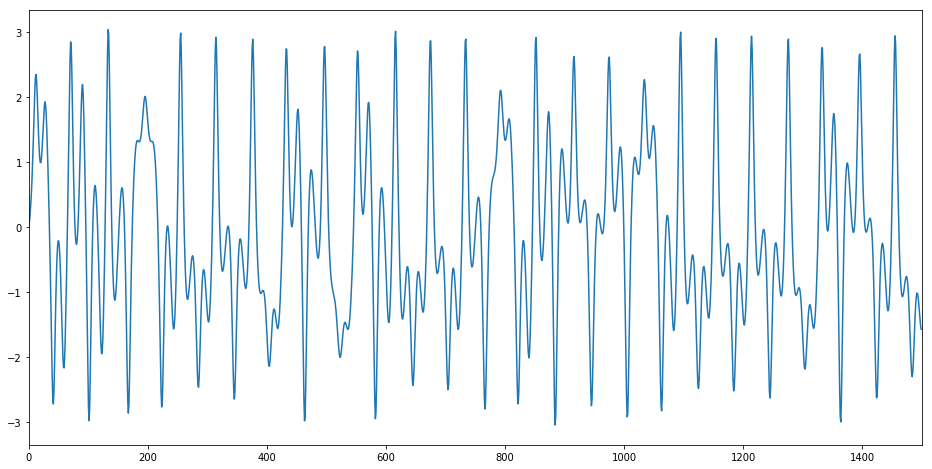
ちなみにこれは「Pythonでカオス・フラクタルを見よう！」で紹介されていたDuffing振動子の時系列データです。データ生成もこちらのコードからお借りしています。

import tensorflow as tf
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from model import EchoStateNetwork

#get Duffing time series data
data = np.loadtxt("DuffingOscillatorData.txt")

plt.figure(figsize=(16,8))
plt.plot(data)
plt.xlim(0, len(data))

それでは、窓幅16でデータを作成します。

window_size_d = 16
pred_length_l = 1

def create_sliding_window_data(X, window_size, pred_length):
    data = [X[i:i+window_size] for i in range(len(X)-window_size-pred_length)]
    target = [X[i+window_size:i+window_size+pred_length] for i in range(len(X)-window_size-pred_length)]
    return np.array(data,dtype=np.float32), np.array(target,dtype=np.float32)

X_windows, y_windows = create_sliding_window_data(data,window_size_d,pred_length_l)
X_train, X_test, y_train, y_test = train_test_split(X_windows, y_windows, test_size=0.8,shuffle=False)
X_train = np.expand_dims(X_train,axis=2)
X_test = np.expand_dims(X_test,axis=2)

後はデータをモデルに入れるだけです。
scikit-learnに慣れてる人なら一目瞭然です。

#Run ESN
ESN = EchoStateNetwork(units=32)
ESN.fit(X_train, y_train)
print("Train MSE:",ESN.MSE_Score(X_train, y_train))
print("Test MSE:",ESN.MSE_Score(X_test, y_test))
y_test_hat = ESN.predict(X_test)

結果を可視化するとこうなりました。

緑の部分が学習範囲です。難解なカオスな時系列を、たったの300点しか学習していないのに、凄まじい精度で予測出来ていますね。

#まとめ
本記事では、リザーバコンピューティングの基本技術であるESNについて、解説と実装を紹介しました。
難解なカオス時系列での実験では驚くほどうまくフィットし、リザーバコンピューティングのポテンシャルの大きさを認識しました。
なお、本記事のコードは全てこちらにアップしております。

#文献
M. Lukos̆evicius, A Practical Guide to Applying Echo State Networks, Neural Networks: Tricks of the Trade, Lecture Notes in Computer Science, vol. 7700.