NTT データ数理システムでリサーチャーをしている大槻 (通称、けんちょん) です。
好きなアルゴリズムは最小カットやマッチングですが、会社ではなぜか「DP が好きな人」と呼ばれています。今回は、最近注目度が急上昇している AtCoder について記します。本記事は chokudai さんによるツイートをきっかけにして生まれました。
0. はじめに
AtCoder 株式会社の存在感が日に日に高まっています。
AtCoder は「アルゴリズムを題材とした問題をプログラミングを使って解く」ことを競技化したコンテストを開催するサイト、およびその運営会社です。2012 年 6 月 20 日に設立されて以来、年々活動の幅を拡げて来ました。
コンテストの運営を定期的に行ったり、優秀な学生を発掘することで各企業のソフトウエアエンジニア採用の支援を行う事業 (例: CODE FESTIVAL, ドワンゴからの挑戦状) を行ったり、ソフトウェアエンジニアの能力判定 PAST (Practical Algorithm Skill Test) を実施したりしています。
しかしながら、AtCoder に登録したはいいものの次に何をしたらいいかわからずに途方に暮れてしまう方も多いという話をよく聞きます。そこで本記事では AtCoder 登録からコンテスト常連になるまでの道筋を示すことを目標にします。
本記事を基にした AtCoder 公式コンテンツ
AtCoder 上に本記事で精選した問題たちを集めたページがあります!
実際にソースコードを提出してジャッジすることができます。
目次
| 章 | タイトル | 備考 |
|---|---|---|
| 0. | はじめに | |
| 1. | AtCoder とは | |
| 2. | AtCoder への登録 | |
| 3. | Hello World --- practice contest (A 問題のみ) | |
| 4. | practice の次は??? | ここをしっかりフォローします! |
| 5. | 過去問精選 10 問! | 本記事のメインコンテンツです |
| 6. | コンテストに参加しよう! | |
| 7. | AtCoder 以外のコンテスト | ここからは参考情報まとめです |
| 8. | AtCoder に関連したサービスたち | |
| 9. | 今後コンテスト生活を送るためのおススメ tips | |
| 10. | 参考書 | 今後の勉強の参考に |
| 11. | おわりに |
本記事を終えた次は?
AtCoder Beginners Selection を終えたら、AtCoder 上の過去問が
に集大成されていますので、片っ端から埋めるような気持ちで精進していきましょう。本記事の続編として
も執筆しましたので参考にしていただけたらと思います。また、アルゴリズムとデータ構造に関するトピックを集大成した書籍として、
- 問題解決力を鍛える!アルゴリズムとデータ構造 (通称、けんちょん本)
を上梓しました。ぜひ読んでみてください。
1. AtCoder とは
AtCoder は以下のコンテストサイトを運営しています。今後常に訪れることになるサイトです:
さて、そもそもプログラミングコンテストが何者なのか、ピンと来ない方も多いでしょう。ざっくり言うとプログラミングコンテストとは
プログラミングを使って、パズル的な問題を、制限時間内に出来るだけ多く解くスポーツ
です。謎解きや、ボルダリングをやっている方であれば、それらのプログラミングバージョンだと言うとイメージが近いと思います。下の方で実際の過去問を解いていきますので、本記事を読み終える頃には雰囲気が掴めていると思います。

(「勉強か?趣味か?人生か?―プログラミングコンテストとは」より引用)
プログラミングコンテスト自体について深く知りたい方は以下の記事がとてもよいです:
また最近は競技プログラミングという単語もよく目にするようになりました。これはプログラミングコンテストのうち、特にアルゴリズム系の問題を短時間で解くタイプのものを指します。ゲーム AI 開発コンテストや、Kaggle といった機械学習系コンテストなど、もっと広い意味でのプログラミングコンテストについて知りたい方は以下の記事がとてもよいです:
2. AtCoder への登録
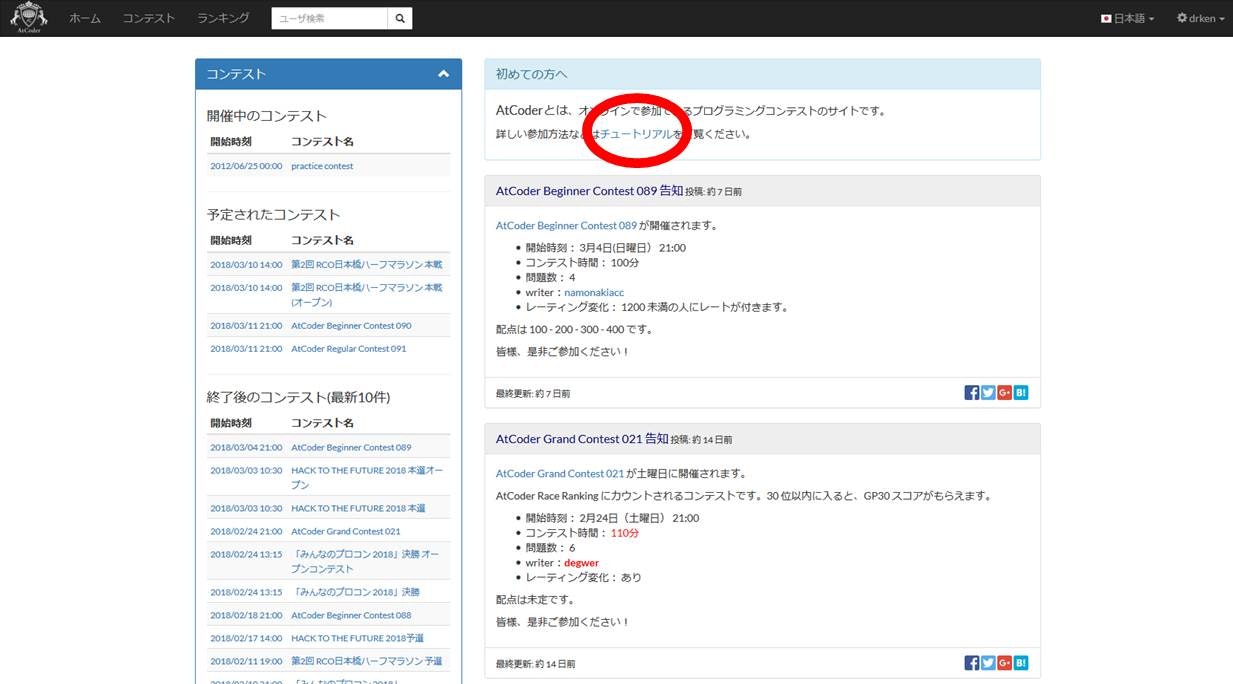
「AtCoder に登録したら次にやること」と題しつつも、一応登録からやります。まずは
にアクセスします。
上図の赤く囲ったところをクリックすると、登録画面になります。必要項目を入力して「新規登録」を押すだけです。超簡単!!!!!!!最高!!!!!!! TopCoder のあの大変な登録手続きはなんだったのか...
3. Hello World --- practice contest (A 問題のみ)
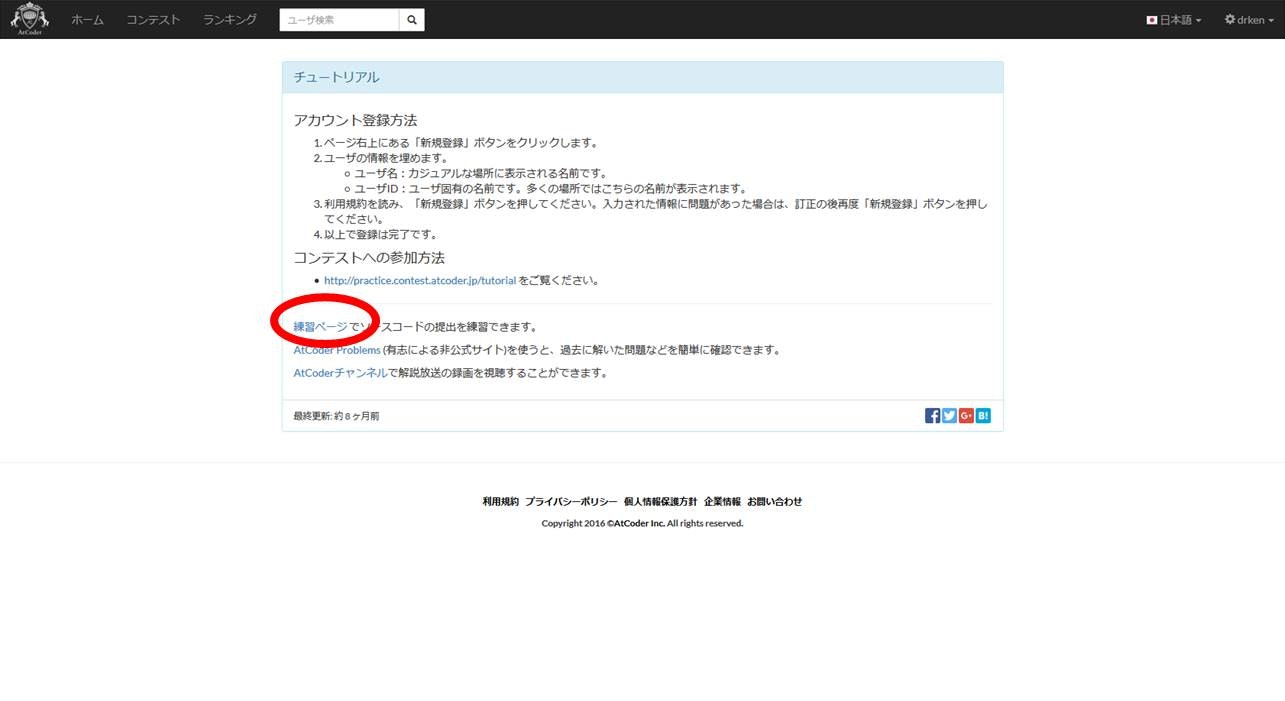
まずは Hello World ということで、practice contest の A 問題を解いてみましょう。
上図の赤く囲ったチュートリアルをクリックします。チュートリアルページには、AtCoder を始めるための情報が一通り書いてあります。ここでは「練習ページ」へと進みます。
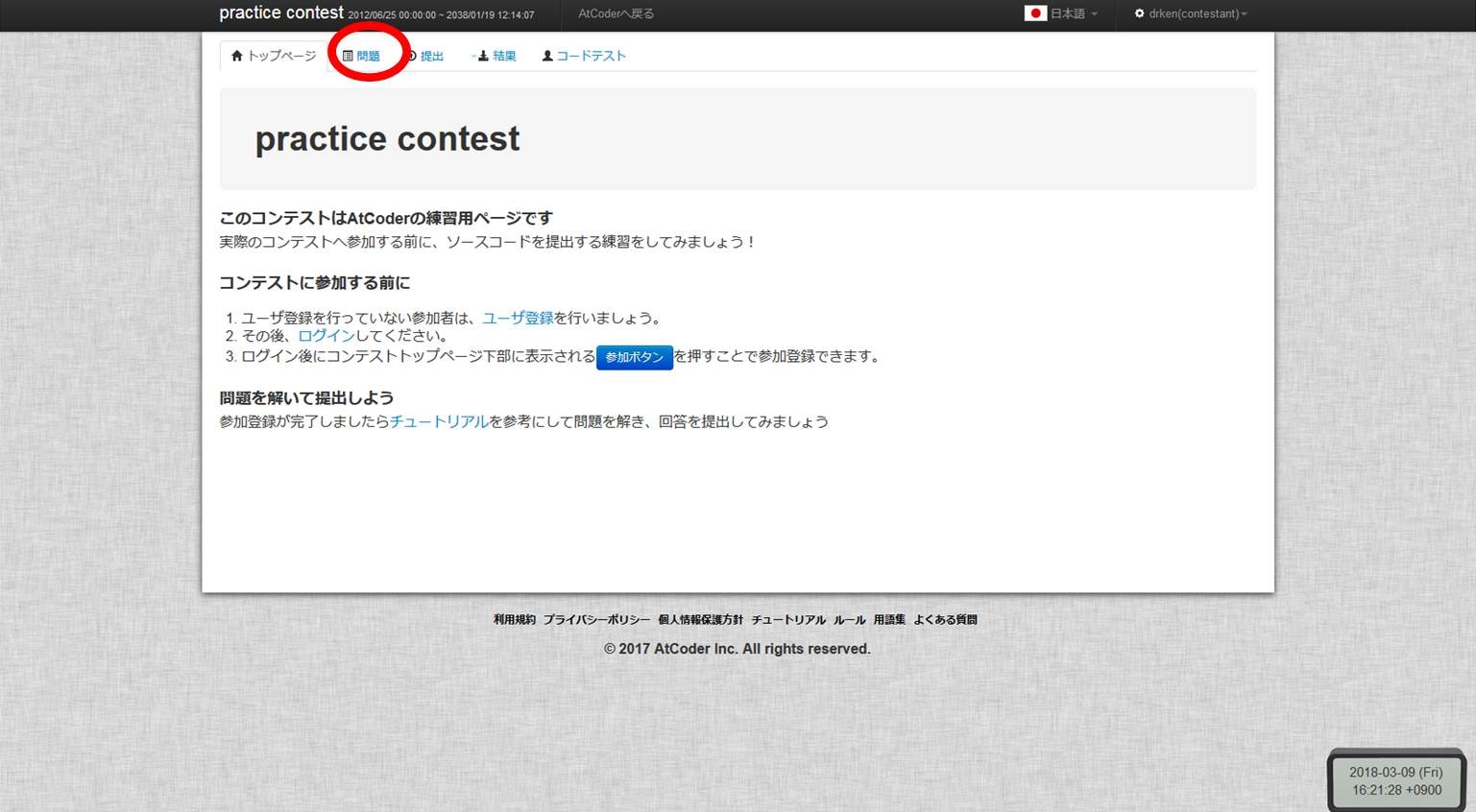
「問題」タブ (下図で赤く囲ったところ) を押すと、問題一覧が登場します。
問題は以下の 2 問があります:
注意点として、今回はこのうちの A 問題だけを解きます。B 問題は決して易しい問題ではないので、どうしても関心のある方のみが挑むとよいと思います (B 問題がわからずに挫折してしまわないよう要注意です)。
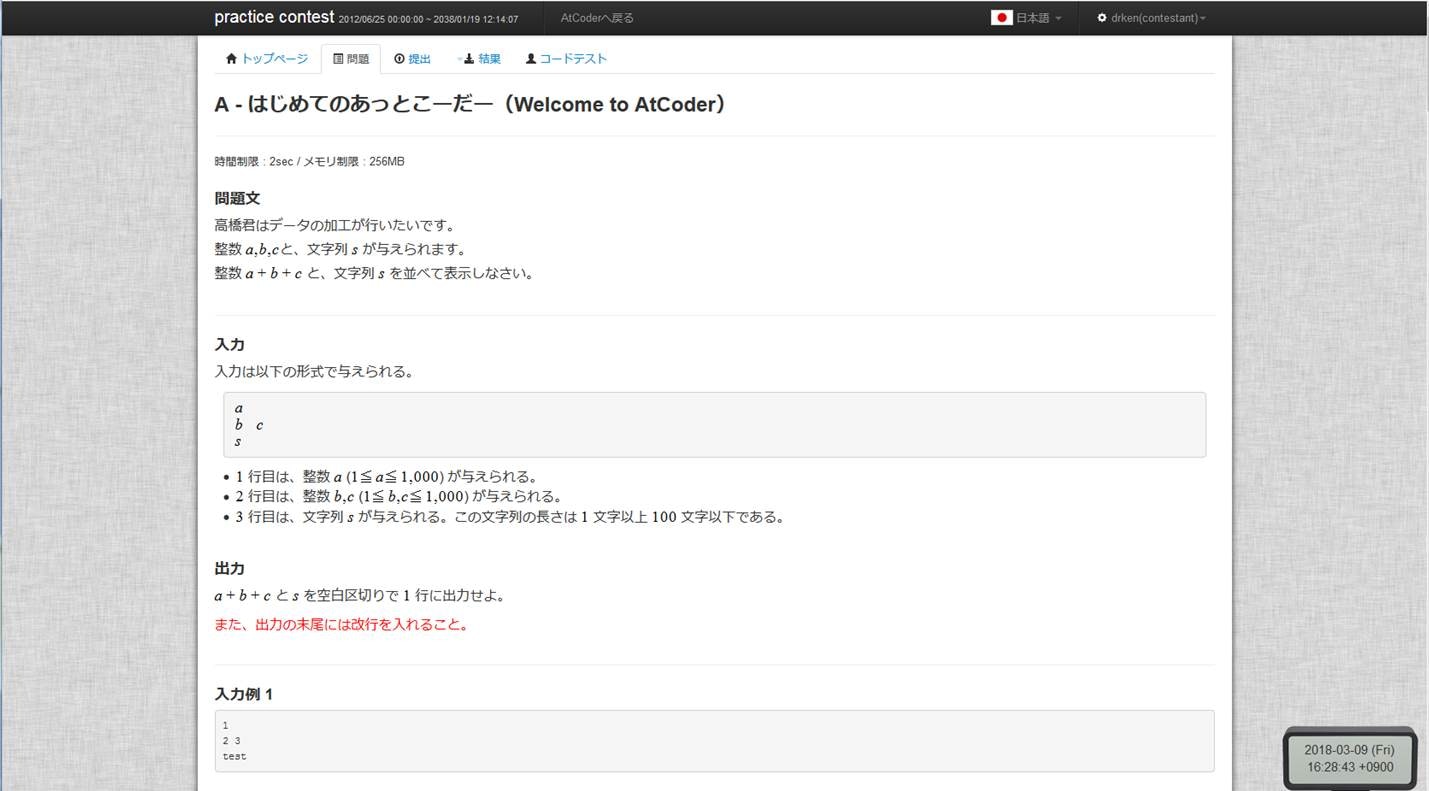
さて、A 問題は以下のような内容です。
この問題の趣旨は、プログラミングスキルの最も基本的なものの 1 つである入出力に慣れようというものです。やることは、整数 a, b, c と文字列 s を受け取って、整数 a+b+c, 文字列 s を出力するというものです。C++ でコーディングすると以下のようになるでしょう (C++ で標準入力を受け取るときに、a と b, c との間の改行はあまり意味がないことに注意):
# include <iostream>
# include <string>
using namespace std;
int main() {
int a, b, c;
string s;
cin >> a >> b >> c;
cin >> s;
cout << a + b + c << " " << s << endl;
}
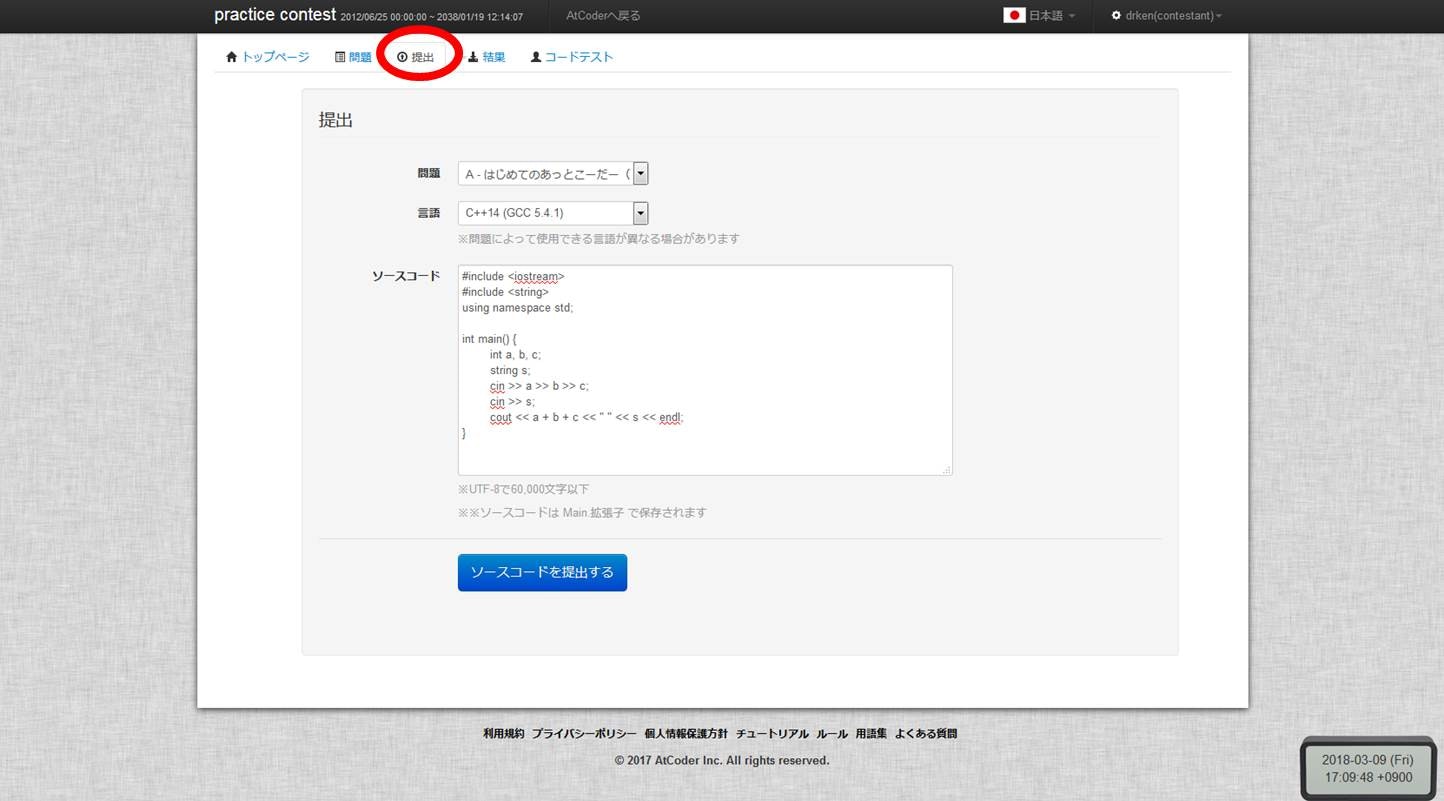
これを提出してみます。上の「提出」タブを押すと提出フォームが登場するので、そこにソースコードを張り付けて「ソースコードを提出する」を押します。あるいは「提出」ページに行かなくても、「問題」ページを下の方にスクロールすると提出フォームが登場するので、そこから提出することもできます。
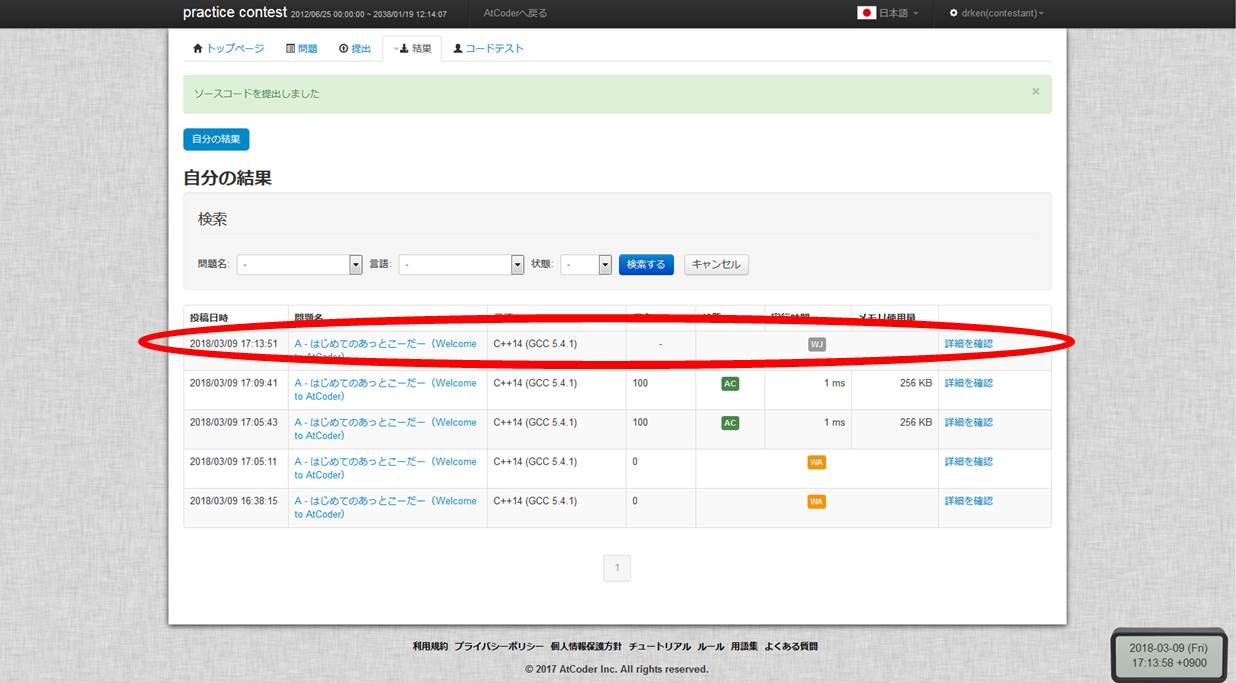
そうすると、下のような画面が登場して、今提出したコードのステータスは赤く囲った一番上の行に表示されます。
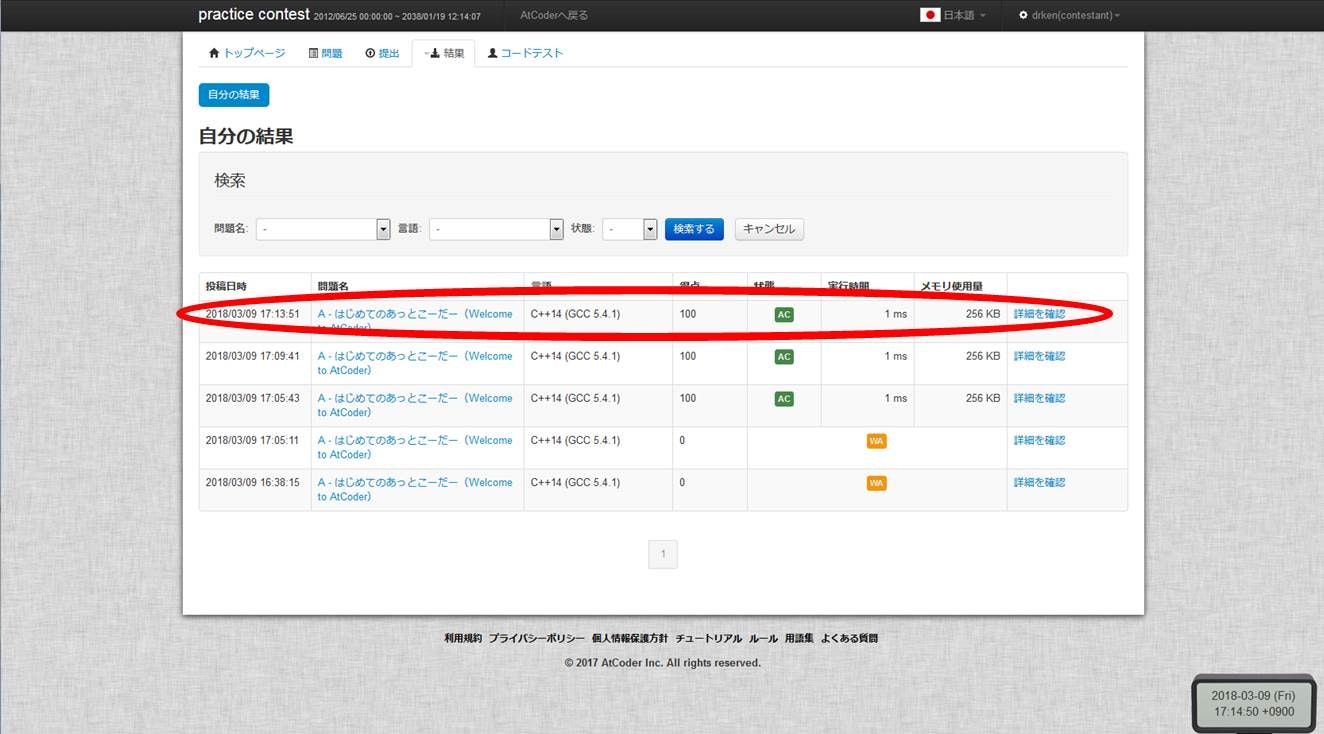
提出直後は灰色の文字で「WJ」と書かれていますが、これは Waiting Judge の略です。しばらく経って F5 を押すと、
となって、緑色で「AC」と表示されます。これは Accepted の略で、無事に正解できたことを表しています。なお、その下の方の行に橙色で「WA」というのがありますが、これは Wrong Answer の略で、提出したソースコードが間違っていたことを表しています。
注意 1: Accepted の判断基準とは
「プログラミングコンテストでは何をしたら正解とみなされるの?」とよく聞かれます。AC の基準はとても単純明快です:
- 予め 10 ~ 200 ケースほどの入力ファイルが用意されていて、それぞれについて想定出力値が用意されている
- 提出したソースコードを実行して、すべての入力ケースに対して、正しい出力を返せば AC となる
- ただし、「ソースコードの実行時間は各ケースにつき 2 秒以内」といった制限時間 (メモリ制限も) が設けられている
スペシャルジャッジなど細かい例外はあるのですが、概ねこのようなルールでジャッジされています。Twitter などを見ていると「嘘解法で通した」という言葉をよく見かけますが、間違った解法だろうと、想定解法よりも遅い解法だろうと、とにかく通れば正義です。この明快さがプログラミングコンテストのよいところだと思います。反対に問題を準備する側としては、嘘解法で通されないように最大限の注意を払っていくことになります。
注意 2: 結局 B 問題はなんだったのか?
B 問題は「初めてインタラクティブ問題を解く人のための練習問題」です。通常の問題は
- 初めに入力をすべて受け取る
- 題意に沿った出力をする
という形式ですが、インタラクティブ問題は
- 初めに入力を受け取る (このフェーズがないこともある)
- こちらが出力する
- それに合わせた入力を受け取る
- ...
- 最終的な答えを出力する
という形式のものです。インタラクティブ問題は初めのうちはほとんど目にすることはない (初心者用コンテスト AtCoder Beginner Contest での過去出題数は 1 回のみ) ですし、上級レベルになっても 100 問に 1 問くらいの頻度です。インタラクティブ問題に初めて挑むようになっている頃には、すでに相当強くなっているはずで、そうした方がインタラクティブ形式の動作確認をするための練習問題です。
4. practice の次は???
そうです、ここで多くの方が挫折してしまいます。
practice までは流れでやってみたものの、次にどうしたらいいかわからずに AtCoder から離れてしまう方が多いと聞いています。個人的には以下の 2 つの流れがあると思います:
こればかりは性格が影響すると思います。もし「とにかくやってみよう」という精神の持ち主であれば、すぐにでもコンテストに参加してみるのが圧倒的によいと思います。コンテストと言っても
- AtCoder Beginner Contest (通称 ABC、初級者向け)
- AtCoder Regular Contest (通称 ARC、中上級者向け)
- AtCoder Grand Contest (通称 AGC、あらゆる層向けだが最上級者も楽しめる内容)
- 企業コンテスト (ドワンゴからの挑戦状など、就活を意識したものがほとんど)
- その他 (ここから先は AtCoder Official ではないもの)
- JAG コンテスト
- JOI 予選
- 大学主催コンテスト (UTPC, KUPC など)
- その他の個人コンテスト
と多種多様ですが、定期的に開催されているのは上の 3 つ (ABC, ARC, AGC) で、そのうちの ABC は
- 競技プログラミングが真に初めてな方でも解ける問題も出題される
- アルゴリズムに関する知識を必要としない問題も出題される
という内容です。つまり ABC に関しては AtCoder での提出方法さえわかっていれば十分挑める内容になっているので、特別な知識などを勉強するよりも先にガンガン参加していくのがよいと思います。むしろコンテストに参加することで勉強すべき事柄が分かって来るので、その状態で様々なアルゴリズムを勉強していくのが効率いいと言えるでしょう!
しかしそうは言っても、未知のコンテストに飛び込むのは怖いものです。そこで本記事では、過去問を 10 問精選して「どんな問題が出題されるのか」「自分はどのくらい解けるのか」という感覚を掴んでいただけるように試みました。コンテストに参加する足がかりにしていただけたらと思います。
なお、本番の ABC でどの程度解けるとどの程度のパフォーマンス値が出るかについて予め詳しく知りたい方は、
を読んでいただけたらと思います。
5. 過去問精選 10 問!
まず始めに、AtCoder の過去問に挑むにあたって、以下のような素晴らしいサービスがあります:
ここに今まで AtCoder 上で出題されたコンテストの問題たちが集大成されています。このうちの、「AtCoder Beginner Contest」の欄が当面のターゲットになります。
ここで注意点なのですが、人間というものは「まずは第一回の問題から解いてみよう」と思うのが自然の成り行きです。しかしながら ABC は長い試行錯誤の歴史の中で育まれて来ましたので、
ABC 001 と現在の ABC とでは問題の傾向が大きくかけ離れています!!!!!
従って、まずは問題の傾向がハッキリと固まって来た 2016 年以降の問題を解いていくのがよいと思います。具体的には、ABC 042 ~最新です。
さて、それでは過去問を解いていきましょう!
精選した 10 問のうち、2 問が 100 点問題 (A 問題)、5 問が 200 点問題 (B 問題)、3 問が 300 点問題 (C 問題) になっています。ただし後半 2 問についてはかなり難しいので、8 問目まで解くだけでも大体の感触はつかめると思います。
第 1 問: ABC 086 A - Product (100 点)
【問題概要】
二つの正整数 $a$, $b$ が与えられます。 $a$ と $b$ の積が偶数か奇数か判定してください。
【制約】
- $1 \le a, b \le 10000$
- $a$, $b$ は整数
【数値例】
1)
$a = 3$
$b = 4$
答え: Even
3 × 4 = 12 でこれは偶数なので、"Even" を出力します。
$a = 1$
$b = 21$
答え: Odd
1 × 21 = 21 でこれは奇数なので、"Odd" を出力します。
【キーポイント】
- 四則演算
- 倍数判定
【解法】
まずは、Fizz Buzz でもおなじみの、倍数判定をする問題です!
素直に a * b を計算して、2 の倍数かどうかを判定すればよいでしょう。
# include <iostream>
using namespace std;
int main() {
int a, b;
cin >> a >> b;
int c = a * b;
if (c % 2 == 0) cout << "Even" << endl;
else cout << "Odd" << endl;
}
【コメント】
倍数判定はもっと広くとらえると「余りを求める処理」です。というのも「2 で割り切れる」というのは「2 で割った余りが 0 である」ということを意味するからです。
発展的話題として「余りを切り上げる処理」があります。例えば、「17 人を 3 人ずつグループに分けて、余ったところは 1 つのグループとしたときに何グループできるか」という問題を考えると、
17 ÷ 3 = 5 あまり 2
で、3 人グループが 5 個と、余った 2 人によるグループが 1 個できるので、合計 6 個のグループができます。一般に、「a 人を b 人ずつグループに分けると何グループできるか?」は
- a が b で割り切れるとき: a/b
- a が b で割り切れないとき: a/b + 1
になります。しかし実はこれをまとめて (a + b - 1) / b と簡潔に書くことができます。今後頻繁に使うことになるテクニックなので習得しておきたいところです。
【類題】
- ABC 064 A - RGB Cards (同じく倍数判定です)
- ABC 088 A - Infinite Coins (倍数判定の発展として、余りを計算します)
- ABC 157 A - Duplex Printing (余りを切り上げる処理をします)
第 2 問: ABC 081 A - Placing Marbles (100 点)
【問題概要】
0 と 1 のみから成る 3 桁の番号 s が与えられます。1 が何個含まれるかを求めてください。
【数値例】
1)
s = "101"
答え: $2$
'1' が 2 個含まれています。
【キーポイント】
- for 文を使わない程度の全探索
- string 型
【解法】
全探索は競プロにおいてすべての基本です。これはその最も簡単な例題であると言えます。慣れた人ならむしろ for 文を使いたくなるかもしれません。豆知識として、ABC A 問題は、for 文を知らなくても解けるように作られています。
また、入力の受け取り方は様々な方法が考えられると思いますが、string 型で処理するのが楽だと思います。string 型に慣れる練習も兼ねて解いてみましょう!
# include <iostream>
# include <string>
using namespace std;
int main() {
string s;
cin >> s;
int counter = 0;
if (s[0] == '1') ++counter;
if (s[1] == '1') ++counter;
if (s[2] == '1') ++counter;
cout << counter << endl;
}
【コメント】
string 型について他によく使用するメソッドとしては (変数名を s, t とします)
- 文字列の長さ: s.size()
- 文字列の i 文字目: s[i] (char 型です、値の取得も書き換えもできます)
- 文字列の連結: s + t (例: s = "AtCoder", t = "Jobs" -> s + t = "AtCoderJobs")
- 文字列の大小関係: < (辞書式順序で比較します)
があります。
【類題】
- ABC 095 A - Something on It (非常によく似た問題です)
- ABC 085 A - Already 2018 (string 型を扱う練習です)
- ABC 069 B - i18n (B 問題ですが for 文不要で難しくなく、string 型を扱うよい練習問題です)
- ABC 082 B - Two Anagrams (辞書順最小に関する理解を問います、B 問題なので少し難しくなります、下に出て来るソートも使います)
第 3 問: ABC 081 B - Shift Only (200 点)
【問題概要】
黒板に $N$ 個の正の整数 $A_1, \dots, A_N$ が書かれています。
すぬけ君は,黒板に書かれている整数がすべて偶数であるとき,次の操作を行うことができます。
- 黒板に書かれている整数すべてを,$2$ で割ったものに置き換える。
すぬけ君は最大で何回操作を行うことができるかを求めてください。
【制約】
- $1 \le N \le 200$
- $1 \le A_i \le 10^9$
【数値例】
1)
$N = 3$
$A = (16, 12, 24)$
答え: $2$
1 回操作を行うと (8, 6, 12) になります。2 回操作を行うと (4, 3, 6) になります。2 個目の 3 が奇数なため 3 回目の操作は行えません。
【キーポイント】
- for 文を用いた全探索
- シミュレーション
【解法】
ついにここから 200 点問題に入ります!
200 点問題からはいよいよ for 文を用いる問題が登場します。この問題は大きく 2 つの考え方がありますが、ここでは愚直に問題文に書かれた通りの「操作」を、操作を行えなくなるまで実行する方法で解いてみましょう。
# include <iostream>
using namespace std;
int N;
int A[210]; // 最大 200 個なので余裕を持って 210 に --- 200 以上ならなんでもよいです
int main() {
cin >> N;
for (int i = 0; i < N; ++i) cin >> A[i];
int res = 0;
// 操作が行える限り操作を繰り返す
while (true) {
bool exist_odd = false; // A[i] がすべて偶数かどうかを判定するフラグ
for (int i = 0; i < N; ++i) {
if (A[i] % 2 != 0) exist_odd = true; // 奇数があったらフラグを立てる
}
if (exist_odd) break; // 奇数があったら break
// 操作を行えるなら操作を実際に行う
for (int i = 0; i < N; ++i) {
A[i] /= 2;
}
++res; // 操作回数をインクリメント
}
cout << res << endl;
}
【コメント】
この例題のもう 1 つ解き方については線形探索記事も参考にしていただけたらと思います。
【類題】
- ABC 068 B - Break Number (例題によく似た問題です)
- ABC 102 B - Maximum Difference (できれば for 文を 1 回だけ使って解いてみましょう)
- ABC 113 B - Palace (最小値を求めるだけでなく、最小になる index を求める書き方も確認しましょう)
- ABC 072 B - OddString (文字列に対する for 文も、数列に対する for 文と同様です)
- ABC 053 B - A to Z String (同じく文字列に対する for 文です)
- ABC 095 B - Bitter Alchemy (max や sum といった、for 文テクニックの総動員です)
第 4 問: ABC 087 B - Coins (200 点)
【問題概要】
500 円玉を $A$ 枚、100 円玉を $B$ 枚、50 円玉を $C$ 枚持っています。これらの硬貨の中から何枚かを選び、合計金額をちょうど $X$ 円にする方法は何通りあるでしょうか?
【制約】
- $0 \le A, B, C \le 50$
- $A + B + C \ge 1$
- $50 \le X \le 20000$
- $A, B, C$ は整数である
- $X$ は $50$ の倍数である
【数値例】
1)
$A = 2$
$B = 2$
$C = 2$
$X = 100$
答え: $2$
条件を満たす選び方は以下の 2 通りです。
- 500 円玉を 0 枚、100 円玉を 1 枚、50 円玉を 0 枚選ぶ
- 500 円玉を 0 枚、100 円玉を 0 枚、50 円玉を 2 枚選ぶ
【キーポイント】
- for 文を用いた全探索
- 二重三重の for 文
【解法】
さあ今度は for 文がネストする処理を実装します!
これも全探索シリーズの一員ですが、複雑度が少しアップしました。この例題では
- 500 円玉が 0 枚 〜 A 枚の場合 (A + 1 通り)
- 100 円玉が 0 枚 〜 B 枚の場合 (B + 1 通り)
- 50 円玉が 0 枚 〜 C 枚の場合 (C + 1 通り)
をすべて探索します。全部で、(A + 1)(B + 1)(C + 1) 通りの場合があります。
# include <iostream>
using namespace std;
int main() {
int A, B, C, X;
cin >> A >> B >> C >> X;
int res = 0;
for (int a = 0; a <= A; ++a) {
for (int b = 0; b <= B; ++b) {
for (int c = 0; c <= C; ++c) {
int total = 500*a + 100*b + 50*c; // 合計金額
if (total == X) ++res; // 合計金額が X に一致したら答えをインクリメント
}
}
}
cout << res << endl;
}
【コメント】
このような多重 for 文は慣れないうちは頭がごっちゃになるかもしれません。このような多重 for 文タイプの全探索に慣れることが競プロの重要なステップになります。
なおこの問題を見て、数学的考察をしようと頑張った方も多いかもしれません。しかし実際は素直に for 文を回す全探索を行えば解ける問題でした。ABC の B 問題までであれば数学的に深い知識が要求されることはほとんどないので、こうした素直な全探索を着想できるようになることが大切だと思います。より高度な問題であっても、過度に数学的考察に走ってしまって DP といった素直な解法が取れなくなることも競プロあるあるです。
【類題】
- ABC 105 B - Cakes and Donuts (Coins にとてもよく似た問題です)
- ABC 144 B - 81 (与えられた整数が掛け算九九に含まれるかを判定する問題です)
- ABC 133 B - Good Distance ($N$ 個のアイテムから 2 個選ぶ方法のうち、条件を満たすものが何個あるかを数える問題です)
- ABC 175 B - Making Triangle ($N$ 個のアイテムから 2 個選ぶ方法のうち、条件を満たすものが何個あるかを数える問題です)
第 5 問: ABC 083 B - Some Sums (200 点)
【問題概要】
$1$ 以上 $N$ 以下の整数のうち、$10$ 進法で各桁の和が $A$ 以上 $B$ 以下であるものについて、総和を求めてください。
【制約】
- $1 \le N \le 10^4$
- $ 1 \le A \le B \le 36$
- 入力はすべて整数
【数値例】
1)
$N = 20$
$A = 2$
$B = 5$
答え: $84$
20 以下の整数のうち、各桁の和が 2 以上 5 以下なのは、2, 3, 4, 5, 11, 12, 13, 14, 20 です。これらの合計である 84 を出力します。
【キーポイント】
- 整数の 10 進法表記の扱い方
- for 文
【解法】
整数の 10 進法表記に関する出題は ABC の B 問題でよく見られるテーマです。
例えば 834 の各桁の和は 8 + 3 + 4 = 15 ですが、このような処理をプログラムする方法を考えなければなりません。これには以下のような定石があります:
834 を 10 で割った余りは 4 -> 答えに加算
834 を 10 で割って 83
83 を 10 で割った余りは 3 -> 答えに加算
83 を 10 で割って 8
8 を 10 で割った余りは 8 -> 答えに加算
8 を 10 で割って 0
0 なので break
あとはこの処理を素直にソースコードにすればよいです。
# include <iostream>
using namespace std;
// 各桁の和を計算する関数
int findSumOfDigits(int n) {
int sum = 0;
while (n > 0) { // n が 0 になるまで
sum += n % 10;
n /= 10;
}
return sum;
}
int main() {
int N, A, B;
cin >> N >> A >> B;
int total = 0;
for (int i = 1; i <= N; ++i) {
int sum = findSumOfDigits(i); // i の各桁の和
if (sum >= A && sum <= B) { // i の各桁の和が A 以上 B 以下かどうか
total += i;
}
}
cout << total << endl;
}
【コメント】
はじめのうちは頭が混乱するかもしれませんが、慣れると毎回決まり切った書き方になるので難しくはないです。発展的話題として、2 進法や 3 進法や 16 進法など、10 進法以外の n 進法への書き換えなどがあります。これもほとんど同じ実装で実現することができます (2 進法についてはビットシフト演算子を使いこなしたいところです)。
【類題】
- ABC 090 B - Palindromic Numbers (同じく整数の 10 進法表記に関する問題です)
- AGC 025 A - Digits Sum (同じくです)
- ABC 156 B - Digits ($K$ 進法に関する問題です)
第 6 問: ABC 088 B - Card Game for Two (200 点)
【問題概要】
$N$ 枚のカードがあり、$i$ 枚目のカードには $a_i$ という数が書かれています。
Alice と Bob はこれらのカードを使ってゲームを行います。ゲームでは 2 人が交互に 1 枚ずつカードを取っていきます。Alice が先にカードを取ります。
2 人がすべてのカードを取ったときゲームは終了し、取ったカードの数の合計がその人の得点になります。2 人とも自分の得点を最大化するように最適戦略をとったとき、Alice は Bob より何点多くの得点を獲得できるかを求めてください。
【制約】
- $N$ は $1$ 以上 $100$ 以下の整数
- $a_i$ は $1$ 以上 $100$ 以下の整数
【数値例】
1)
$N = 3$
$a = (2, 7, 4)$
答え: $5$
以下が最適です:
- 1 ターン目: Alice が 7 を取る
- 2 ターン目: Bob が 4 を取る
- 3 ターン目: Alice が 2 を取る
Alice は 7 + 2 = 9 点、Bob は 4 点を獲得するので、その差は 9 - 4 = 5 点です。
【キーポイント】
- ソート
- Greedy
【解法】
来ました!ソートです!
ついに競プロらしさが徐々に出て着ます。ソートはアルゴリズム学習者が最初に詳しく学ぶものですが、競プロ的には std::sort() を使いこなせるようになればほとんどの場面で十分です。C++ では std::sort() ですが、他の多くの言語でもソート処理はサポートされています。
さて、この問題は一見とっつきにくいですが、最適戦略はとても簡単です。2 人とも残ってるカードの中から最も大きい値を取ればよいです。具体的には、配列 a を大きい順にソートして、前から順に 2 人が交互に取って行けばよいです。
下のソースコードの注意点として、sort(a, a+N, greater<int>()) の greater<int>() について解説します。これをなくして sort(a, a+N) とすると配列 a[0:N] は値が小さい順にソートされてしまいます。今回はどちらかと言うと大きい順にソートしたいので、それを指定するために greater<int>() をつけています (小さい順にソートしておいて後ろから交互に取る実装方法もあります)。
# include <iostream>
# include <algorithm>
using namespace std;
int main() {
int N;
int a[110]; // 最大 100 個ですが余裕をもたせます
cin >> N;
for (int i = 0; i < N; ++i) cin >> a[i];
sort(a, a + N, greater<int>()); // a[0:N] を大きい順にソート
int Alice = 0;
int Bob = 0;
for (int i = 0; i < N; ++i) {
if (i % 2 == 0) { // Alice のターン
Alice += a[i];
}
else { // Bob のターン
Bob += a[i];
}
}
cout << Alice - Bob << endl;
}
【コメント】
ソートを自在に使いこなせるようになると、解ける問題の幅が大きく拡がります。
【類題】
- ABC 067 B - Snake Toy (ソートです)
- ABC 042 B - Iroha Loves Strings (ソートする対象が文字列になります)
- AGC 027 A - Candy Distribution Again (ソートして小さい順に配って行きます)
- AGC 012 A - AtCoder Group Contest (少し難しめのソート問題です、是非挑戦してみましょう)
第 7 問: ABC 085 B - Kagami Mochi (200 点)
【問題概要】
$N$ 個の整数 $d[0], d[1], \dots, d[N-1]$ が与えられます。
この中に何種類の異なる値があるでしょうか?
(原問題文をかなり意訳していますが、題意はこういうことです)
【制約】
- $1 \le N \le 100$
- $1 \le d[i] \le 100$
- 入力値はすべて整数
【数値例】
1)
$N = 4$
$Q = 3$
$d = (8, 10, 8, 6)$
答え: $3$
6, 8, 10 の 3 種類です。
【キーポイント】
- 集計処理
- バケット法
- 連想配列
【解法】
これもまた ABC の B 問題や C 問題で超頻出の集計処理です。
B 問題ではバケット法といって、配列 num を用意しておいて、
num[i] := 値 i が何個あるか
とすれば十分なケースがほとんどです。C 問題ではこの i の値が大きくなるため単純な配列では通用しなくなる出題が登場します (i が大きいと単純な配列でダメなのはメモリが足りないためです、その場合は連想配列と呼ばれるものを用います、C++ では std::map 、Python では dictionary が使えます)。
この問題についても、std::set や std::map を用いて解くこともできます。
// バケット法による解
# include <iostream>
using namespace std;
int main() {
int N;
int d[110];
cin >> N;
for (int i = 0; i < N; ++i) cin >> d[i];
int num[110] = {0}; // バケット
for (int i = 0; i < N; ++i) {
num[d[i]]++; // d[i] が 1 個増える
}
int res = 0; // 答えを格納
for (int i = 1; i <= 100; ++i) { // 1 <= d[i] <= 100 なので 1 から 100 まで探索
if (num[i]) { // 0 より大きかったら
++res;
}
}
cout << res << endl;
}
// std::set を用いた解
# include <iostream>
# include <set>
using namespace std;
int main() {
int N;
int d[110];
cin >> N;
for (int i = 0; i < N; ++i) cin >> d[i];
set<int> values; // insert するときに重複を取り除いてくれます
for (int i = 0; i < N; ++i) {
values.insert(d[i]); // 挿入します
}
// set のサイズを出力します
cout << values.size() << endl;
}
【コメント】
今後は単なる集計処理の枠組みを超えて、バケット法が暗黙に使える場面は劇的に増えていきます。ビットを用いた複数フラグ管理もバケット法の一種と言えますし、バケットを Binary Indexed Tree に乗せて k 番目に小さい値を求める処理を高速に実行する話題があります (Binary Indexed Tree は高級な話題なので現時点では無理に勉強しなくても大丈夫です)。
【類題】
- ABC 071 B - Not Found (アルファベットは結局 0 〜 25 という値と同じことです)
- ABC 061 B - Counting Roads (ちょっとした応用問題です)
- ABC 047 B - Snuke's Coloring 2 (ABC Edit) (二次元配列を用意します)
- ABC 091 B Two Colors Card Game (std::map が使えると楽です)
- ABC 081 C - Not so Diverse (C 問題ですが十分挑めます、バケット法とソートの複合問題です)
第 8 問: ABC 085 C - Otoshidama (300 点)
【問題概要】
10000 円札と、5000 円札と、1000 円札が合計で $N$ 枚あって、合計金額が $Y$ 円であったという。このような条件を満たす各金額の札の枚数の組を 1 つ求めなさい。そのような状況が存在し得ない場合には -1 -1 -1 と出力しなさい。
【制約】
- $1 \le N \le 2000$
- $1000 \le Y \le 2*10^7$
- $N$ は整数
- $Y$ は $1000$ の倍数
【数値例】
1)
$N = 9$
$Y = 45000$
答え: $(4, 0, 5)$ など
10000 円札 4 枚と 1000 円札 5 枚で、合計枚数が 9 枚、合計金額が 45000 円になります。他の答えもあります。
【キーポイント】
- for 文を用いた全探索
- 二重三重の for 文
- 少し工夫が必要
【解法】
ここからついに 300 点問題です!!!
200 点問題までは「計算実行時間」のことはほとんど何も考えなくても解くことができました。300 点問題からは計算時間のことを意識する必要が生じます。
さて、まず最初に思い浮かぶ解法は、以下のような for 文を三重ループで回す解法でしょう。すなわち、10000 円札を a 枚、5000 円札を b 枚、1000 円札を c 枚として、(a, b, c) のありうる組合せを全探索します。
for (int a = 0; a <= N; ++a) {
for (int b = 0; b <= N; ++b) {
for (int c = 0; c <= N; ++c) {
int total = 10000a + 5000b + 1000*c;
if (a + b + c == N && total == Y) {
// 見つかった!
}
}
}
}
しかしこのとき調べる場合の数は $(N + 1)^3$ 通りになります。今、$N$ としてありうる最大値は $2000$ ですので、ざっくり $+1$ を除くと $2000^3 = 8,000,000,000$ 通りも調べることになります。ここで重要な知見として
1 秒間で処理できる for 文ループの回数は、$10^8 = 100,000,000$ 回程度
というのがあります。ざっくりとしていますが、今後いかなるときも常に頭に置いておく目安です。さて、これでは制限時間 2 秒以内に計算実行するは厳しいことがわかると思います。工夫が必要なのですが、よく考えると最後の
for (int c = 0; c <= N; ++c)
が不要であることに気がつきます。なぜなら、$a + b + c = N$ であることが最初から条件として課せられているため、$a$, $b$ が決まれば、$c = N - a - b$ と自動的に決まります。そうすると for 文ループは二重で済み、今度はざっくりと $2000^2 = 4,000,000$ なので制限時間内に計算実行を終えることができます。
# include <iostream>
using namespace std;
int main() {
int N, Y;
cin >> N >> Y;
int res10000 = -1, res5000 = -1, res1000 = -1;
for (int a = 0; a <= N; ++a) { // 10000円の枚数を 0 〜 N で調べる
for (int b = 0; b + a <= N; ++b) { // 5000円の枚数を 0 〜 N-a で調べる
int c = N - a - b; // 1000円の枚数は決まる
int total = 10000*a + 5000*b + 1000*c;
if (total == Y) { // 答えが見つかったら
res10000 = a;
res5000 = b;
res1000 = c;
}
}
}
// 答えを出力 (見つかっていなくても -1 -1 -1 になるので OK です)
cout << res10000 << " " << res5000 << " " << res1000 << endl;
}
【コメント】
プログラムの計算時間をざっくり見積もる非常に有効な方法として、計算量オーダーと呼ばれる概念があります。初めはとっつきにくいかもしれませんが、慣れると非常に有効な概念です。計算量オーダーの言葉で説明すると、この例題では $O(N^3)$ かかる処理 (for 文三重ループ) を $O(N^2)$ に高速化したと言うことができます。
- 参考: 計算量オーダーの求め方を総整理
【類題】
- ABC 088 C - Takahashi's Information (やはり効率良い探索方法を考えます)
- ARC 096 C - Half and Half (明快な全探索方法を考えましょう、実は O(1) 解法もあります)
- ABC 057 C - Digits in Multiplication ($A$ を全探索すればよいですが、$1 \le A \le N$ のすべてを全探索していては間に合いません、実は $1 \le A \le \sqrt{N}$ だけ調べればよいです)
- ABC 112 C - Pyramid (パズルだと思って解くと難しいかもしれません、探索すればよいと思い至ることが重要です)
第 9 問: ABC 049 C - Daydream (300 点)
【問題概要】
英小文字からなる文字列 $S$ が与えられます。
$T$ が空文字列である状態から始めて、以下の操作を好きな回数繰り返すことで $S = T$ とすることができるか判定してください。
- $T$ の末尾に "dream", "dreamer", "erase", "eraser" のいずれかを追加する。
【制約】
- $1 \le |S| \le 10^5$
- $S$ は英小文字からなる
【数値例】
1)
$S$ = "dreameraser"
答え: "YES"
"dream", "eraser" の順で $T$ の末尾に追加することで $S = T$ とすることができます。
【キーポイント】
- Greedy アルゴリズム
- 端から決まって行く Greedy アルゴリズム
- 後ろから解く
【解法】
一見手がかりが掴めないような問題でありながら、端っこから順に考えると芋づる式に全体が決まって行くタイプの問題は ABC の C 問題では頻出です。これは Greedy アルゴリズムの一種であると言うことができます。
というわけでまずは文字列 $S$ を先頭から順に "dream", "dreamer", "erase", "eraser" に分解していくことを考えてみましょう。しかし例えば上の例題の数値例にあるように、"dreameraser" を先頭から順に 5 文字 dream まで読み進めたときに、そこで切っていいのかそれとも次の er まで進んで dreamer で切るべきなのかを判断することは容易ではなさそうです。
しかしなんと、$S$ を後ろから順に "dream", "dreamer", "erase", "eraser" に分解しようと思うと状況は一変します!
前から読むと "dream" が "dreamer" に完全に被っていました (こういう関係を prefix と呼びます)。しかし後ろから考えると、"dream", "dreamer", "erase", "eraser" のうちのどの 2 つをとってもそのような関係にはありません。したがって、文字列 $S$ が与えられたときに、どこで切って行けばいいのかは後ろから順番に芋づる式に決まって行きます。
# include <iostream>
# include <string>
# include <algorithm>
using namespace std;
string divide[4] = {"dream", "dreamer", "erase", "eraser"};
int main() {
string S;
cin >> S;
// 後ろから解くかわりにすべての文字列を「左右反転」する
reverse(S.begin(), S.end());
for (int i = 0; i < 4; ++i) reverse(divide[i].begin(), divide[i].end());
// 端から切っていく
bool can = true;
for (int i = 0; i < S.size();) {
bool can2 = false; // 4 個の文字列たちどれかで divide できるか
for (int j = 0; j < 4; ++j) {
string d = divide[j];
if (S.substr(i, d.size()) == d) { // d で divide できるか
can2 = true;
i += d.size(); // divide できたら i を進める
}
}
if (!can2) { // divide できなかったら
can = false;
break;
}
}
if (can) cout << "YES" << endl;
else cout << "NO" << endl;
}
【コメント】
「後ろから解く」という発想は少し難しいかもしれませんが、何気によく出て来る考え方です。ただし今回後ろから芋づる式に解くことができたのはたまたまだと言えます。実際、前から解いても後ろから解いても「どこで切ったらいいかわからない」という問題設定を考えることもできます。そのような状況で有力な手法として動的計画法 (DP) と呼ばれる手法があります。この例題も DP によって前から解くことも可能です。なお DP までしなくても、前から深さ優先探索 (DFS) や幅優先探索 (BFS)、少し先まで見る Greedy などの解法によってゴリ押すこともできます。これらの別解法については、@259_Momone さんの以下の記事を参考にしていただければと思います:
なお、ある文字列が他の文字列の prefix になっているかどうかというのは、文字列の問題において極めて重要な概念です。今後 Suffix Array などを学ぶときに思い出すとよいと思います。
【類題】
- AGC 013 A - Sorted Arrays (数列の端から順にできるだけ長い列を切り出す Greedy です)
- AGC 011 A - Airport Bus (同様に小さい方から順に切り出して行く Greedy です)
- ABC 059 C - Sequence (最初の a[0] を正か負かを決めると芋づる式に決まります)
- ABC 072 C - Together (X を決めると Greedy にすべて決まります)
第 10 問: ABC 086 C - Traveling (300 点)
【問題概要】
シカの AtCoDeer くんは二次元平面上で旅行をしようとしています。AtCoDeer くんの旅行プランでは、時刻 $0$ に 点 $(0, 0)$ を出発し、$1$ 以上 $N$ 以下の各 $i$ に対し、時刻 $t_i$ に 点 $(x_i, y_i)$ を訪れる予定です。
AtCoDeer くんが時刻 $t$ に 点 $(x, y)$ にいる時、 時刻 $t+1$ には 点 $(x+1,y), (x−1,y), (x,y+1), (x,y−1)$ のうちいずれかに存在することができます。その場にとどまることは出来ないことに注意してください。AtCoDeer くんの旅行プランが実行可能かどうか判定してください。
【制約】
- $1 \le N \le 10^5$
- $0 \le x_i, y_i \le 10^5$
- $1 \le t_i \le t_{i+1} \le 10^5$
- 入力はすべて整数
【数値例】
1)
$N = 2$
$(t, x, y) = (3, 1, 2), (6, 1, 1)$
答え: "Yes"
例えば $(0,0), (0,1), (1,1), (1,2), (1,1), (1,0), (1,1)$ と移動すれば目的を果たせます。
【キーポイント】
- パリティ
【解法】
「偶数」と「奇数」に関する性質をパリティと言います。
とりあえず $i$ -> $i+1$ の移動について考えることが重要なので、$dt = t_{i+1} - t_{i}$, $dist = {\rm abs}(x_{i+1} - x_{i}) + {\rm abs}(y_{i+1} - y_{i})$ とおきます。まず明らかに、$dist > dt$ のときは不可能です。以降は $dist \le dt$ として考えます。
ここでパリティに関する考察が登場します!
$x_i + y_i$ という値の偶奇に着目します。実は $(x_i, y_i)$ という値は様々な値を動きますが、$x_i + y_i$ は毎秒ごとに必ず偶奇が入れ替わることがわかります。すなわち、$dt$ が偶数ならば、$dist$ は偶数でなければなりません。反対に $dt$ が奇数ならば、$dist$ は奇数でなければなりません。逆にこの条件を満たしていれば「行ったり戻ったり」を駆使しながら必ずたどり着くことができます。
このように、
- 毎ステップごとにある量の偶奇が入れ替わる
- どのステップもある量の偶奇が変化しない (という問題もある)
といったことに着目するのは、AtCoder では頻出です!
# include <iostream>
using namespace std;
int main() {
int N;
int t[110000], x[110000], y[110000];
cin >> N;
t[0] = x[0] = y[0] = 0; // 初期状態
for (int i = 0; i < N; ++i) cin >> t[i+1] >> x[i+1] >> y[i+1]; // 1-index にしておく
bool can = true;
for (int i = 0; i < N; ++i) {
int dt = t[i+1] - t[i];
int dist = abs(x[i+1] - x[i]) + abs(y[i+1] - y[i]);
if (dt < dist) can = false;
if (dist % 2 != dt % 2) can = false; // dist と dt の偶奇は一致する必要あり!
}
if (can) cout << "Yes" << endl;
else cout << "No" << endl;
}
【コメント】
関連する話題として、「グリッドを市松模様に塗る」という手法があります (これにより、グリッドグラフは二部グラフの一種であることがわかります)。今回の例題も「市松模様に塗られた格子点上を 1 ターン移動する度に白黒が入れ替わっている」ととらえることもできます。今後頻出のテクニックになりますので、頭の片隅に入れておくと良さそうです。
【類題】
- ABC 093 C - Same Integers (今度は「不変量」に着目します)
- AGC 010 A - Addition (AGC ですが A 問題は 300 点前後であることが多いです、パリティのよい例題です)
- AGC 020 A - Move and Win (やはりパリティのよい例題です)
- ABC 073 C - Write and Erase (連想配列またはソートとの複合問題です)
ここまで解いたら
ここまで解いて来たらもう AtCoder で出題される問題に対するイメージはかなり掴めていると思います!あとはひたすら過去問を埋めるような気持ちで片っ端から解いていきましょう。
100 点問題と 200 点問題については、残りは以下のような項目を勉強すれば完璧だと思います:
| トピック | 例題 | 備考 |
|---|---|---|
| グリッドに関する処理 | ABC 075 B, ABC 096 C | 今後超頻出です |
| 区間の重なりを求める処理 | ABC 070 B | 今後頻出です |
| 答えを 1000000007 (など) で割った余りで求める | ABC 055 B | 途中計算ごとに % をとってよいことを理解しましょう |
| 数学的問題 | ABC 046 B, ABC 048 B | |
| 状態がループするシミュレーション処理 | ABC 060 B, ABC 065 B | 今後頻出の考え方です |
| 累積和 | ABC 087 C, ABC 098 C | 今後超頻出のテクニックです |
| bit 全探索 | ABC 079 C | $2^n$ 通りを調べる手法です |
300 点問題については、ここで取り上げきれなかったトピックもありますが、以下の記事も併せて読んでいただければ、300 点問題の範囲全体もほぼカバーできると思います:
6. コンテストに参加しよう!
さて、ここまで問題を解けば、AtCoder でどんな問題が出題されるのか、雰囲気を掴めたと思います。もう迷わずにコンテスト (まずは ABC) に参加しましょう!
コンテスト参加するときの注意点や tips を以下にまとめました:
7. AtCoder 以外のコンテスト
AtCoder 以外の様々なコンテストやオンラインジャッジについて、以下の記事にまとめました:
なお、Paiza 開発日誌の
にも似たような情報があるのですが、AtCoder の格付けは 2015 年当時からかなり上昇したと思います。
8. AtCoder に関連したサービスたち
AtCoder 生活を楽しくするために様々な人によって様々なサービスが作られています。AtCoder Problems (kenkoooo さん) はその代表格と言えますが、他にも様々なものがあります。以下のページによくまとまっています:
- AtCoderでの競技プログラミングがもっと楽しくなるサイトまとめ (Noimin さん)
また、大量の過去問の中から自分の解くべき問題を選ぶためのサービスとして
- AOJ-ICPC (ichyo さんと有志たち)
- AOJ/AtCoder-JOI (goodbaton さんと有志たち)
があります。AtCoder 上の過去問や、ICPC に関連した問題の難易度や、JOI に関連した問題の難易度が評価されていて、自分に合った難易度の問題を選ぶのによいサービスです。また、AtCoder を含めた様々なコンテストの開催日時のチェックには
- Competitive Programming Contests Calendar (hotpepsi さん)
がよいでしょう。
9. 今後コンテスト生活を送るためのおススメ tips
強くなるための方法論
強くなるためには、やはりなんといってもコンテストに出ることが重要だと思います。過去問を解いているときに解けなかった問題と、コンテスト中に解けなかった問題とでは悔しさが段違いですので、コンテストに出ることでより効率よくトピックを吸収できます。そのためには復習することが極めて大事です。この辺りのことは AtCoder 社長が記事にまとめています:
Twitter のススメ
意外かもしれませんが Twitter は競技プログラミングで強くなっていくためには、ほぼ必須のツールだと言えます。多くの競技プログラマたちが、コンテスト参加後には Twitter 上で盛んに問題の議論を交わしています。コンテスト後でなくても、普段から様々な問題に関する議論で賑わっています。とても古い記事ですが、AtCoder 社長による以下の記事があります:
現在は引退している選手の情報も多く含んでいるので古いですが、Twitter が重要なことが感じとれると思います。
10. 参考書
競技プログラミングにのめり込んで行く上で参考になる書籍などを挙げていきます。
プログラミングコンテスト攻略本
三大攻略本と言われるのは、蟻本、螺旋本、チーター本で、難易度は「蟻本 > 螺旋本 > チーター本」という感じです。
- プログラミングコンテストチャレンジブック (通称、蟻本)
まずはなんといっても競技プログラミング界のバイブル、蟻本です!
6 年前に秋葉さん・岩田さん・北川さんによって執筆されて以来、誰もが手にするバイブルとなりました。現在では競技プログラミング用参考書という域を超えて、世界的なアルゴリズムの教科書の 1 つと言える立ち位置までになっています。際立った特徴として、洗練された C++ による実装が載っていることが挙げられるでしょう。行間をぎゅっと絞っているので、スピード感があって爽快な反面、説明を読み解くのが難しいという声も多々聞きます。しかしながら蟻本に書いてある内容は、読み解くことさえできたならば、非常に濃密なものと感じられます。
- 最強最速アルゴリズマー養成講座 プログラミングコンテストTopCoder攻略ガイド (通称、チーター本)
AtCoder 社長による競技プログラミング入門用書籍です。蟻本は対象者層が中上級者向けで難しいと言われていますが、チーター本は競技プログラミングを始めたばかりの人に目線を合わせた真の入門書です。蟻本と同様、例題の出典サイト (チーター本の場合は topcoder) が現在メジャーでないという問題を抱えているものの、丁寧でわかりやすい解説が売りです。C++ だけでなく Java や C# での実装も載っているのが特徴です。ただし丁寧な反面、やや重いのが弱点です。「これを読まないと螺旋本・蟻本に進めない」と思ってしまうと気が遠くなるので、もっと気軽に読むと「強くなるための良いヒントが沢山書いてある」本です。
- プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 (通称、螺旋本)
彗星のように素晴らしい書籍が登場しました。螺旋本・AOJ 本・TLE 本などと呼ばれています。対象層は入門を終えた初中級者向けで、蟻本より易しく、チーター本より難しい程度です。あらゆる層の人にとって読みやすい書籍と言えそうです。例題ももちろん AOJ 上でジャッジできる問題たちなので安心感があります。
Google, Microsoft, Facebook, Amazon, Apple などでは選考過程で実際にコーディングを行うことはすっかり有名になりました。それら筆頭の人気あるトップ IT 企業で行われるプログラミング面接に合格し採用されるための攻略本として米国では絶大な人気を誇るベストセラー書となっています。なお新版もあるのですが日本語訳に誤植が多く注意が必要です。
ICPC の日本大会を主催する方々が中心となって書かれた書籍です。
アルゴリズム系書籍
アルゴリズムの世界的教科書の 1 つです。蟻本が出版されてからはこの本で勉強する日本人は少なくなりましたが、現在なお色褪せない価値のある本です。競技プログラミング界隈では典型という言葉が盛んに議論されることがあります。最大流アルゴリズムといった様々なアルゴリズムを最もシンプルな形で適用できるような問題を典型と呼ぶのだとすると、アルゴリズムデザインは典型を網羅した本だと言えるでしょう。中上級者でも改めて読み返すと学ぶ要素がある本です。
同じくアルゴリズムの世界的教科書です。アルゴリズムデザインがアルゴリズムの使い方に焦点を当てた本だとすると、アルゴリズムイントロダクションはアルゴリズムの原理に焦点を当てた本だと言えます。直観的には正しいと思えるような様々なアルゴリズムの正当性がきっちりと議論されています。こうしたことをしっかりと学んでおくことは、より難しい問題を解くときに重要になるケースも多いです。
各分野ごとのアルゴリズム系書籍
組合せ最適化の世界的教科書です。少し難しめですが、グラフ理論や離散数学に関連するアルゴリズムの話題が豊富に集められており、学ぶ要素は非常に多いです。
組合せ最適化に関するサーベイは、2003 年までの分についてはこれ一冊でできると言われるほど、グラフ理論や離散数学に関するアルゴリズムを集大成した本です。1881 ページにも及ぶ世界的名著は、組合せ最適化分野における世界的研究者 Alexander Schrijver によって書かれました。
文字列を高速に処理するアルゴリズムについての書籍です。
計算幾何分野に関する書籍です。
整数論や数列など、いわゆる数学ゲーと呼ばれる分野に関する書籍です。
ゲーム分野に関する書籍です。
競技プログラミングに挑む上で解けない問題 (NP-hard, NP-complete, #P-complete) を知ることは大切です。この本を勉強すると、解けない問題を知覚するスキルが磨かれます。
インターネット上の資料など
競技プログラミング界隈は情報共有が非常に活発で、皆が勉強したことを盛んに発信しています。そのため無料で読むことのできる資料が非常に充実しています。ここではその一例を示します:
全般
- 各種アルゴリズムの C++ による実装 (前原さん)
- spaghetti-source/algorithm (前原さん)
通称 spaghetti-source。競技プログラマ以外にも有名なライブラリ集です。様々なアルゴリズムが C++ で実装されています。
- beet-aizu/library (beet さん)
ACM-ICPC 強豪大学の会津大学で育まれているライブラリです。
- 競技プロ的なアルゴリズムのスライドのまとめ (kroton さん)
今までに公開された良質なスライドたちを集めています。
- 競技プログラミング練習問題集 (はまやんさん)
様々な分野の問題たちが並べられています。
- アルゴリズム wiki (はむこさん)
非常にマニアックなトピックについても、その解説へのポインタが充実しています。
- 高校数学の美しい物語 (マスオさん)
競技プログラミングに挑む上で、高校数学の素養は随所で必要になって来ます。高校数学の様々なトピックを学べる良サイトです。
数え上げ
- 数え上げテクニック集 (DEGwer さん)
数え上げに関するテクニックの集大成です。
整数
- 整数論テクニック集 (kirika さん)
整数に関するテクニックの集大成です。
動的計画法 (DP)
- プログラミングコンテストでの動的計画法 (秋葉さん)
- アルゴリズマーの登竜門、「動的計画法・メモ化再帰」はこんなに簡単だった (chokudai さん)
- 典型的な DP (動的計画法) のパターンを整理 Part1 ~ ナップサック DP 編 ~ (けんちょん)
- 競技プログラミングにおける動的計画法問題まとめ (はまやんさん)
- DP高速化 (フェリンさん)
DP は競技プログラミングの登竜門的立ち位置なだけに様々な資料が充実していますね。
データ構造
- プログラミングコンテストでのデータ構造 (秋葉さん)
- プログラミングコンテストでのデータ構造 2 ~平衡二分探索木編~ (秋葉さん)
- プログラミングコンテストでのデータ構造 2 ~動的木編~ (秋葉さん)
秋葉さんによるデータ構造系入門資料たちです。
競技プログラミング入門のための資料たち
競技プログラミングに入門するための手引きの役割を果たしている記事たちを紹介します:
- 競技プログラミングって何? (はじめての高校生向け) (Sifne さん)
- アルゴリズムコンテストの挑み方 (Kinaba さん)
- 初心者向けのABCの問題傾向とその対策 (ヘクトさん)
- 競技プログラミングを始めよう (Arc さん)
- 社会人10年目から始める競技プログラミングのすすめ (kuuso さん)
- 競技プログラミングについて紹介(初心者向け) (iwakiriK さん)
- 初心者こそ、競技プログラミングに挑戦してほしい。髙橋直大の「世界にAtCoderを広める」という夢 (インタ記事)
C++ 以外の言語で
最後に、精選過去問 10 問を各言語で解いた記事たちをまとめます。
実に 35 個以上もの言語を用いて精選過去問 10 問が解かれています!
11. おわりに
ここ数年 AtCoder 参加者が激増していることは、一競技プログラマとしてとても嬉しいです。本記事が少しでも「これから AtCoder を始めよう」という方や「友人に AtCoder を奨めたい」という方の役に立つことができたならば、とても嬉しい気持ちです。