軌道生成や軌道計画、最適制御問題の現代的な数値解の求め方の解説。
【追記2017年3月】
ここで書いている内容の発展系としてpythonのライブラリとして公開しました。
下記で実装している理論はLegendre-Gauss-Lobattoの擬スペクトル法、いまいるページに書いている内容はLegendre-Gaussの擬スペクトル法と内容が異なるので注意です。
https://github.com/istellartech/OpenGoddard
https://istellartech.github.io/OpenGoddard/
OpenGoddard使い方1
OpenGoddard使い方2
OpenGoddard使い方3
OpenGoddard使い方4
【追記ここまで】
個人的にはロケットの軌道計画・軌道生成の基礎のつもり。
軌道生成とは例えば飛翔体の燃料を最小にして狙ったところに飛ばすための角度とかを求めるもの。数学的には最適制御問題と定義できる。
ロケットの教科書では間接法の中の変分法と呼ばれる方法が取られている。これは最適制御問題をハミルトニアンの境界値問題に変換して解いていくものである。
変分法は最適なことが保証されてはいるが、式変形が問題ごとに異なったり直感的ではない変数を定義したりと汎用性がない。数式バリバリいじれるぜ、っていう頭いい人向けの解法。変分法は現代でも使われているみたいだけど計算資源が潤沢に使える今では直接法と呼ばれる方法も実用的になっているとのこと。
直接法は元の連続時間非線形最適制御問題を離散化して非線形計画問題に変換して解くもの。直接法の中でも制御変数のみを離散化するシューティング法と制御変数と状態変数を離散化するDirect Collocation法に別れる。
更に、Direct Collocation法も離散化を単調に分割するのではない擬スペクトル法という手法を取ることで、強く非線形的な問題でも比較的安定して解が収束するとのこと。擬スペクトル法の数学的根拠はガウス求積とかになり、数学的教養が無いと理解が苦しい(自分は諦めた
ここでは、軌道生成のための非線形連続時間最適制御問題をDirect Collocation法の一種である擬スペクトル法、特にLegendre-Gauss擬スペクトル法を用いて非線形最適化問題に変換し、Scipyの最適化モジュールの中にあるSLSQPソルバーを使って数値的に解いた。
ちなみに、航空宇宙系の最適化問題というと大抵”制約有り非線形最小化問題”なことが難解になっている理由だと思っている。
制約無しだったり、線形や2次形式だと、便利なソルバーが山ほど転がってるが、”制約有り非線形”だと途端に難しくなる。ソルバーとしては現代では逐次二次計画法(SQP:Sequential quadratic programming)が有効らしい。
非線形最適化問題のソルバーも汎用のものを単純に使うのではなく、色々な工夫をすることによって大規模問題にも適応出来たり、収束が早くなるみたいで職人技的な部分があるみたい。IPOPTとかSNOPTというソルバーを使う例が見受けられるがここでは、ここではソースコード簡単なこと優先ということでscipy.optimizeのソルバーを用いている。
これを書く最中に、シューティング法も比較しようとしたが、全然収束せず、ツライだけだった。シューティング法は使い所が難しい。考え方は単純だが採用しないほうがよさげ。
例
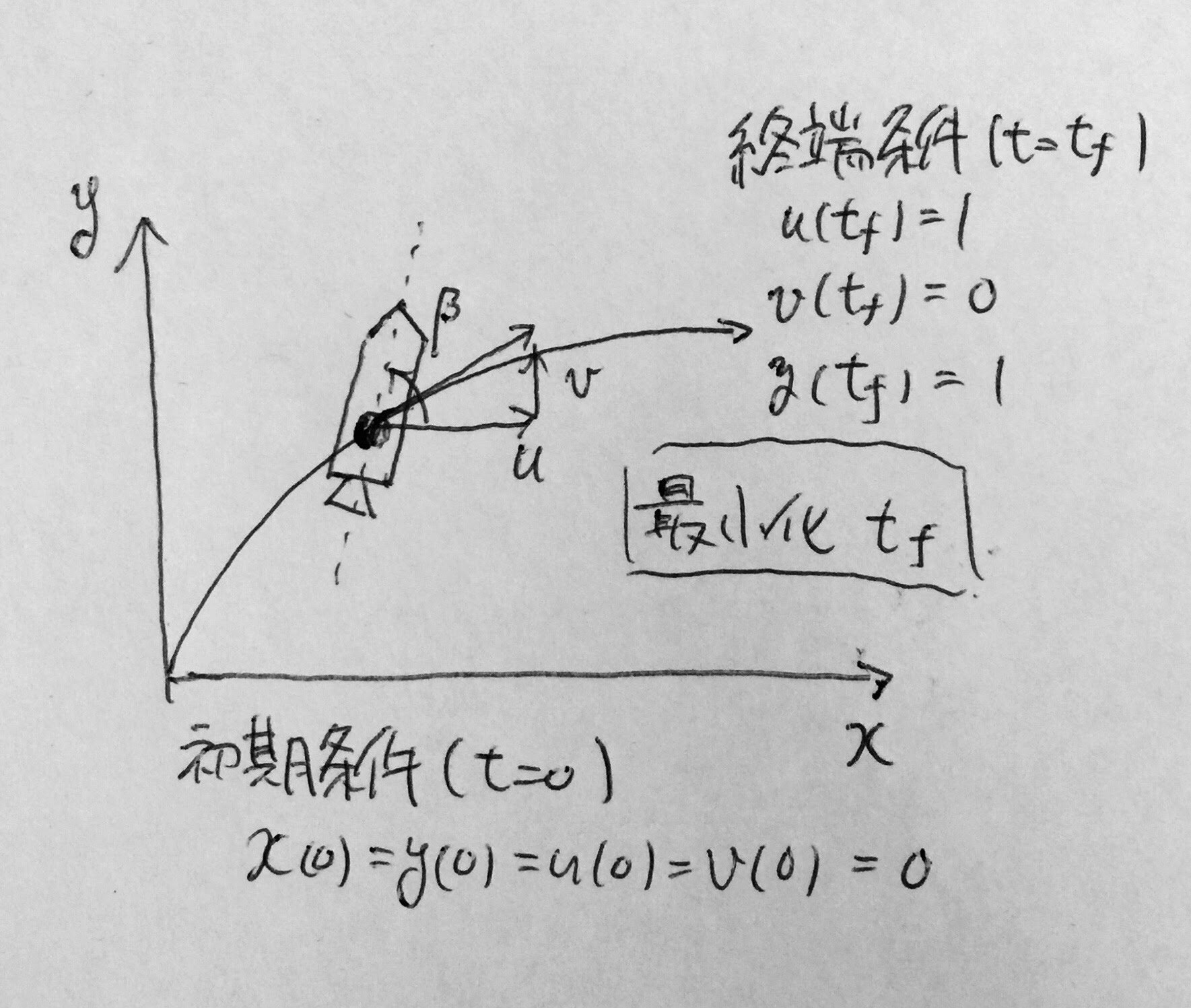
2次元平面上を飛ぶ重力も空気力も受けないロケットが狙いの高度と横速度を得るために燃料最小(飛翔時間最小)の軌道を生成する。
ただし、質量の増減はなく、加速度は一定。大胆に単純化させている。
このときに、初期値、終端条件を定めて、終端時間を評価関数(一番早く行ける軌道)にしいている。
最適制御問題とすると下記のような評価関数と拘束条件になる。
(運動方程式と最適制御問題として数式で記述出来るかどうかが実はかなり肝)
\begin{aligned}
{\rm minimize} & : t_f \\
{\rm subject \ to} & : u(0) = v(0) = x(0) = y(0) = 0 \\
& : u(t_f) = 1,\ v(t_f) = 0, \ y(t_f) = 1 \\
& : -\frac{\pi}{2} \leq \beta \leq \frac{\pi}{2}
\end{aligned}
運動方程式(状態方程式)は下記
\begin{aligned}
\dot{u} & = a \cos \beta \\
\dot{v} & = a \sin \beta \\
\dot{x} & = u \\
\dot{y} & = v
\end{aligned}
ソースコードは下記。ポイントは5つ
- 離散化した時間軸方向の点(Legandre-Gaussノード、ガウス点)と重み、微分行列を求める関数がある
- 最適化する変数を状態変数、制御変数とを離散化した値で1列に並べている
- Direct Collocation法の、数値積分が整合するための拘束条件が入っている
- 数値積分の部分で、系が閉じるように最初から最後まで台形積分した結果が(最後の値)-(最初の値)になるかの拘束条件がある
- 最適化計算の中では時間方向を(-1,1)に正規化?して計算しているので後で元の時間軸に戻す
# -*- coding: utf-8 -*-
# ロケットの最適制御問題、極めて単純化された問題
# 最適制御問題を非線形計画問題に変換して、Scipyの逐次最小2乗法(SLSQP)により解を探索。
# 問題の変更方法は直接法の中でも、Direct Collocation法、更に
# Legendre-Gaussの擬スペクトル法を用いている。
#
# Copyright (c) 2016 Takahiro Inagawa
# Released under the MIT license
import sys
reload(sys)
import platform
# デフォルトの文字コードを変更する.
sys.setdefaultencoding('utf-8')
import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.font_manager
from matplotlib.font_manager import FontProperties
from matplotlib.backends.backend_pdf import PdfPages
import time
if 'Windows' == platform.system():
font_path = r'C:\WINDOWS\Fonts\MSGothic.ttf'
if 'Darwin' == platform.system(): # for Mac
font_path = '/Library/Fonts/Osaka.ttf'
font_prop = FontProperties(fname=font_path)
mpl.rcParams['font.family'] = font_prop.get_name()
plt.close('all')
plt.style.use('ggplot')
mpl.rcParams['axes.grid'] = True
mpl.rcParams['savefig.dpi'] = 300 # defaultのdpi=100から変更
# plt.ion()
def make_node_derivative_matrix(n):
# Legendre-Gauss擬スペクトル法から、collocation pointとしての
# Legendre-Gaussノードと重み、Gauss微分行列(スペクトル微分行列)を計算
# tau: [-1,1]のLegendre-Gaussノード(collocation point)
# w: ガウスの数値積分公式の重み(n個の実数)
# D: Gauss微分行列
beta = np.array([0.5 / np.sqrt(1-(2*i)**(-2)) for i in range(1,n)])
T = np.diag(beta,1) + np.diag(beta,-1) # ヤコビアン
D_, V = np.linalg.eig(T) # 固有値分解
tau = np.sort(D_) # Legendre-Gaussノード(ガウス点)
i = np.argsort(D_)
w = 2 * (V[0,i]**2) # 求積重み
tau = np.hstack((-1,tau,1)) # -1,1(0,N+1)を追加
D = np.zeros([n,n+1]) # Gauss微分行列(ガウス微分行列はかければその点の微分が出るもの)
for k in range(1,n+1):
for l in range(0,n+1):
if k==l:
D[k-1,l] = 0
for m in range(0,n+1):
if m != k:
D[k-1,l] += 1.0/(tau[k]-tau[m])
else:
D[k-1,l] = 1.0/(tau[l]-tau[k])
for m in range(0,n+1):
if m != k and m != l:
D[k-1,l] *= (tau[k]-tau[m])/(tau[l]-tau[m])
return tau, w, D
def dynamics(p, div): # 運動方程式
u = p[1:div[0]-1]
v = p[div[0]+1:div[1]-1]
x = p[div[1]+1:div[2]-1]
y = p[div[2]+1:div[3]-1]
beta = p[div[3]+1:div[4]-1]
dx = np.zeros(0)
a = 1.0 # acceleration
dx0 = a * np.cos(beta)
dx1 = a * np.sin(beta)
dx2 = u
dx3 = v
dx = np.hstack((dx0, dx1, dx2, dx3))
return dx
def evaluation(p, div): # 評価関数
return p[-1]
def equality(p, D, w, t0, div, n): # 等式拘束条件
u = p[0:div[0]-1]
v = p[div[0]:div[1]-1]
x = p[div[1]:div[2]-1]
y = p[div[2]:div[3]-1]
beta = p[div[3]:div[4]-1]
dx = dynamics(p, div)
result = np.zeros(0)
derivative = np.hstack((D.dot(u), D.dot(v), D.dot(x), D.dot(y)))
result = np.hstack((result, derivative - (p[-1]-t0) / 2.0 * dx))
result = np.hstack((result, p[div[0]-1] - p[0] - np.sum(D.dot(u)*w)))
result = np.hstack((result, p[div[1]-1] - p[div[0]] - np.sum(D.dot(v)*w)))
result = np.hstack((result, p[div[2]-1] - p[div[1]] - np.sum(D.dot(x)*w)))
result = np.hstack((result, p[div[3]-1] - p[div[2]] - np.sum(D.dot(y)*w)))
result = np.hstack((result, u[0] - 0.0))
# result = np.hstack((result, p[div[0]-1] - 1))
result = np.hstack((result, v[0] - 0.0))
result = np.hstack((result, p[div[1]-1] - 0))
result = np.hstack((result, x[0] - 0.0))
result = np.hstack((result, y[0] - 0.0))
result = np.hstack((result, p[div[3]-1] - 1))
return result
def inequality(p, D, w, t0, div, n): # 不等式拘束条件
u = p[0:div[0]-1]
v = p[div[0]:div[1]-1]
x = p[div[1]:div[2]-1]
y = p[div[2]:div[3]-1]
beta = p[div[3]:div[4]-1]
dx = dynamics(p, div)
result = np.zeros(0)
result = np.hstack((result, beta + np.pi/2))
result = np.hstack((result, np.pi/2 - beta))
result = np.hstack((result, p[div[0]-1] - 1))
return result
if __name__ == '__main__':
t0 = 0 # 開始時刻
n = 20 # 離散化メッシュ(Legendre-Gaussノード)の個数
num_p = 5 # 状態変数と制御変数の種類合計
iterator = 10 # 最適化の反復数 default:1
tau, w, D = make_node_derivative_matrix(n)
div = [i*(n+2) for i in range(1,num_p+1)] # 変数の変わり目のindex
num_variables = div[-1] + 1 # 状態変数・制御変数・静的変数の全数合計
# 上限・下限ベクトル
# vec_lower_limit = np.zeros(num_variables)
# vec_upper_limit = np.ones(num_variables) * 100
# vec_upper_limit[-1] = 0.5
p = np.ones(num_variables) * 0.5 # 最適化させる変数の初期値
cons = ({'type': 'eq',
'fun': lambda p, D, w, t0, div, n: equality(p, D, w, t0, div, n),
'args': (D, w, t0, div, n,)},
{'type': 'ineq',
'fun': lambda p, D, w, t0, div, n: inequality(p, D, w, t0, div, n),
'args': (D, w, t0, div, n,)})
for i in range(iterator):
opt = minimize(evaluation, p, args=(div,), constraints=cons,
method='SLSQP')
p = opt.x
print(u"iteration: %d" % (i+1))
# 結果の変数を分解
u = p[0:div[0]]
v = p[div[0]:div[1]]
x = p[div[1]:div[2]]
y = p[div[2]:div[3]]
beta = p[div[3]:div[4]]
tf = p[-1]
time = (tf-t0)/2.0 * tau + (tf+t0)/2.0
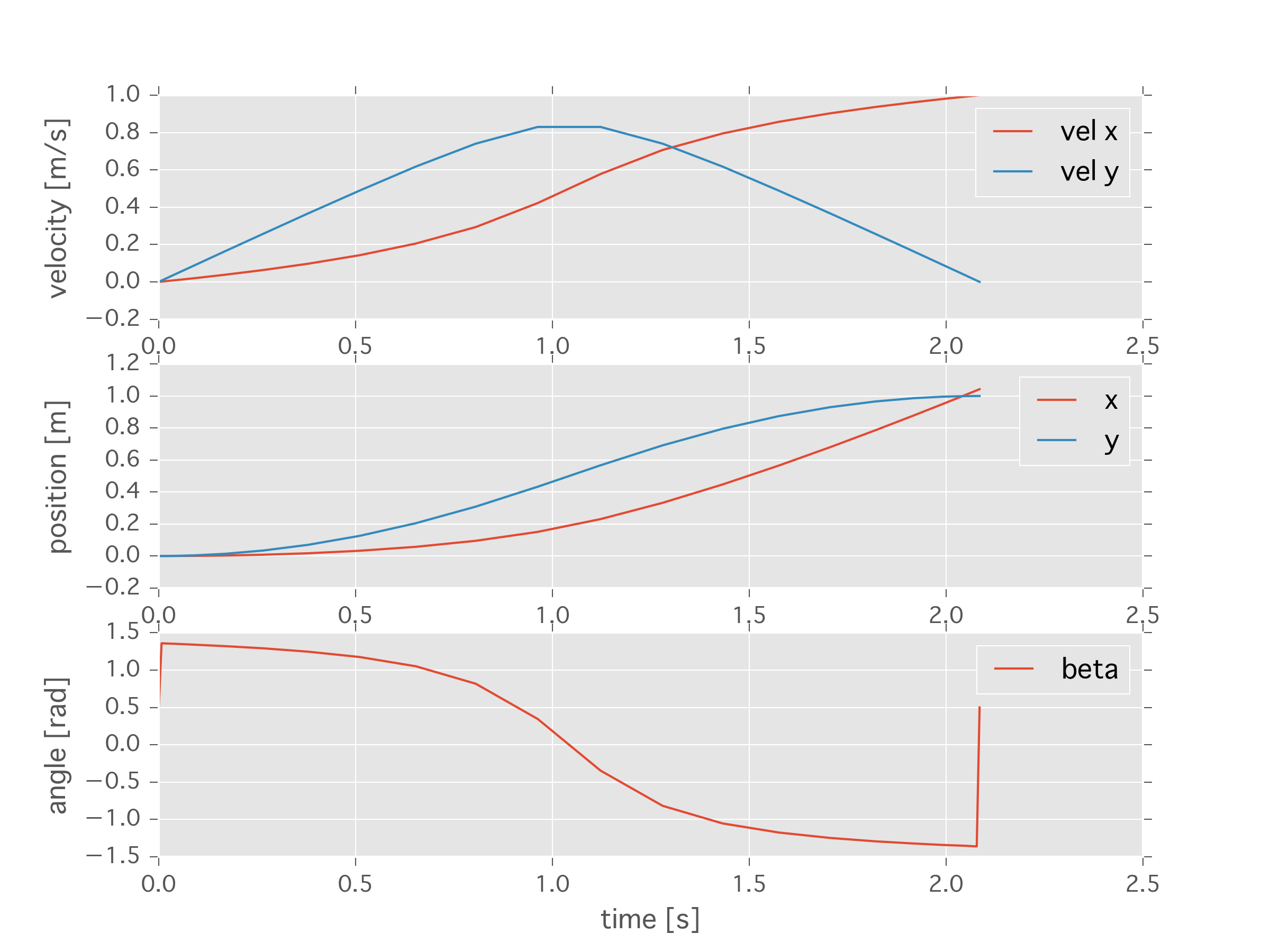
# 結果のPLOT
plt.figure()
plt.subplot(3,1,1)
plt.plot(time,u,label=u"vel x")
plt.plot(time,v,label=u"vel y")
plt.legend(loc="best")
plt.ylabel(u"velocity [m/s]")
plt.subplot(3,1,2)
plt.plot(time,x,label=u"x")
plt.plot(time,y,label=u"y")
plt.legend(loc="best")
plt.ylabel(u"position [m]")
plt.subplot(3,1,3)
plt.plot(time,beta,label=u"beta")
plt.legend(loc="best")
plt.ylabel(u"angle [rad]")
plt.xlabel(u"time [s]")
plt.show()
参考文献
- Benson, David A., et al. "Direct trajectory optimization and costate estimation via an orthogonal collocation method." Journal of Guidance, Control, and Dynamics 29.6 (2006): 1435-1440.
https://goo.gl/BdLsvH (PDF)
↑手法的な元ネタの論文を読むことをオススメ。
加藤 寛一郎 「工学的最適制御―非線形へのアプローチ」 1988年
変分法を使っているので直接は関係が無いが最適制御問題を取り扱っている書籍としては有名どころらしい。
土屋武司, and 鈴木真二. "数理計画法を用いた最適制御問題解法に関する研究 (その 2) ブロック対角へシアン法の提案." 日本航空宇宙学会誌 46.536 (1998): 497-503.
https://www.jstage.jst.go.jp/article/jjsass1969/46/536/46_536_497/_article/-char/ja/
横山信宏, 鈴木真二, and 土屋武司. "スペースプレーンの ISS への上昇軌道最適化に関する研究." JOURNAL OF THE JAPAN SOCIETY FOR AERONAUTICAL AND SPACE SCIENCES 49.570 (2001): 208-213.
https://www.jstage.jst.go.jp/article/jjsass/49/570/49_570_208/_article/-char/ja/
↑東大の鈴木・土屋研の論文はいくつかあるが、とても参考になる。