OpenGoddardの使い方1
OpenGoddardは拙作の非線形最適制御問題の数値解を求めるpythonライブラリです。
https://github.com/istellartech/OpenGoddard
https://istellartech.github.io/OpenGoddard/
ここでは実際の使い方例を説明します。
OpenGoddard使い方1←いまここ
OpenGoddard使い方2
OpenGoddard使い方3
OpenGoddard使い方4
最適化問題
最適制御問題は制約付きの最適化問題のことであり、最適化問題はwikipediaに書いてある通り、評価関数の形や制約条件の有無によって複数の種類があります。
OpenGoddardはその中でも非線形計画問題(nonlinear programming, NLP)=非線形最適制御問題を解くためのライブラリです。
非線形最適制御問題=非線形計画法→[逐次二次計画法](https://ja.wikipedia.org/wiki/%E9%80%90%E6%AC%A1%E4%BA%8C%E6%AC%A1%E8%A8%88%E7%94%BB%E6%B3%95)(sequential quadratic programming, SPQ)で解くということをやっています。
OpenGoddardでは評価関数、運動方程式、拘束条件や計算条件を入れると擬スペクトル法という手法の拘束条件を追加してpythonのScipyの中の逐次二次計画法ソルバー(SLSQP)で解きます。
ユーザーは中身の手法を見ることなく、評価関数・運動方程式(常微分方程式)・拘束条件・計算条件を入れるだけでOKです。
最速降下問題
最適制御問題の古典的な例題で、有名な最速降下問題を例にします。
重力がある場で、摩擦や空気抵抗が無いと仮定した状態で、ボール(質点)が一番早く遠くの距離に達することが出来る曲線(軌道)を求めます。
ググると出てきますが、この曲線はサイクロイド曲線になります。
典型的な最速降下問題のような簡単な例では通常、間接法(変分法)を用います。
数式の変換で解析解を得やすいからです。
しかし、コンピュータリソースの潤沢な現在では、「実用」のためには直接法の方が現実的です。
ということで直接法、特に擬スペクトル法という手法のライブラリである拙作のOpenGoddardを使っていきます。
githubのREADMEに書いているとおり、以下の流れでpythonスクリプトを書いていきます。
- 軌道の最適化をする物体クラスのメソッドと変数の記述
- 運動方程式の関数
- 拘束条件の関数
- 評価関数の関数
- Problemインスタンス生成
- 軌道の最適化をする物体インスタンスの生成
- 最適化変数の正規化のための単位設定(任意)
- 初期値の推定と設置(任意)
- 関数の指定とknotting条件の指定
- solve
- ポストプロセス(可視化)
特に、運動方程式や拘束条件、評価関数を書き下す部分は事前に考えておかないといけませんん。
運動方程式
運動方程式は以下の通りになります。(角度の取り方で文献によって式が異なるので注意)
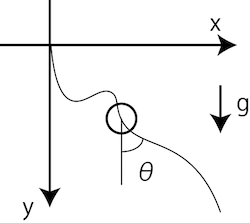
\dot{x} = v \sin{\theta} \\
\dot{y} = v \cos{\theta} \\
\dot{v} = g \cos{\theta}
拘束条件
拘束条件は初期条件、終端条件、物理的に変なことにならないようなヒントを与えていきます。
ここでは、$x=1$に到達、yはどこでも良いという条件にします。
\theta \geq 0 \\
[x(t_0), y(t_0), v(t_0), t0, x(t_f)] = [0, 0, 0, 0, 1] \\
t_f \geq 0
評価関数
最小化する関数を入れます。ここでは「最短時間」での経路を求めたいので、時間を最小化したいです。
J = t_f
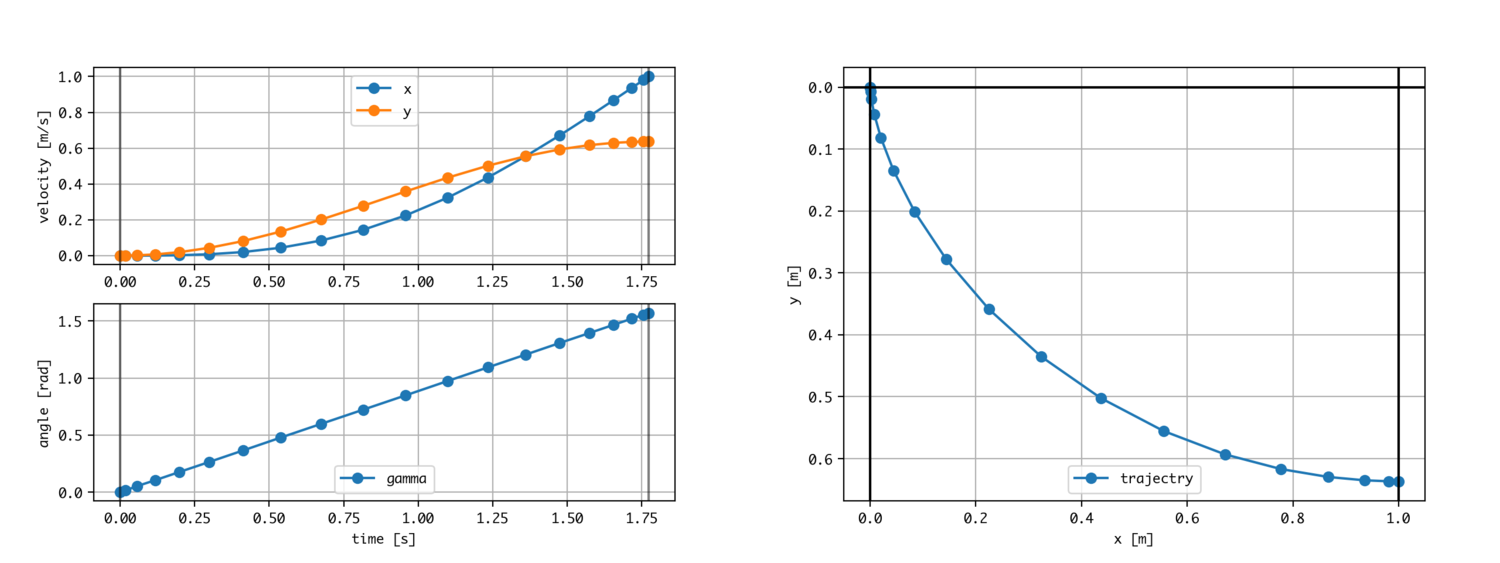
結果
最適化問題を解くのに、状態変数、制御変数のの初期化が必要になります。
初期値を設定しないと全て0として初期化されます。あまり変な値を入れていると解が発散します。特にゼロ割や拘束条件に違反している初期値を入れると解が求まりません。
軌道拘束付き最速降下問題
直接法の強力さを理解するために、最速降下問題に追加の条件を入れてみます。ボール(質点)が入ってはいけない領域(壁)があるという条件を加えてみます。
拘束条件の中に以下を入れます。
y \leq x \tan{\theta_0} + h_0
一方、変分法でも解くことが出来ますが、数式をゴリゴリいじらないと解析解が出てきません。
OpenGoddardのように直接法では解析解のように間違いなく最適という保証はない数値解ではありますが、楽ちんに解が出ます。
ただ、大域最適解ではなく、かならず局所最適解であることも注意してください。
(v1.0.0時点では実装していませんが、最適性が確認できる手法もあります)
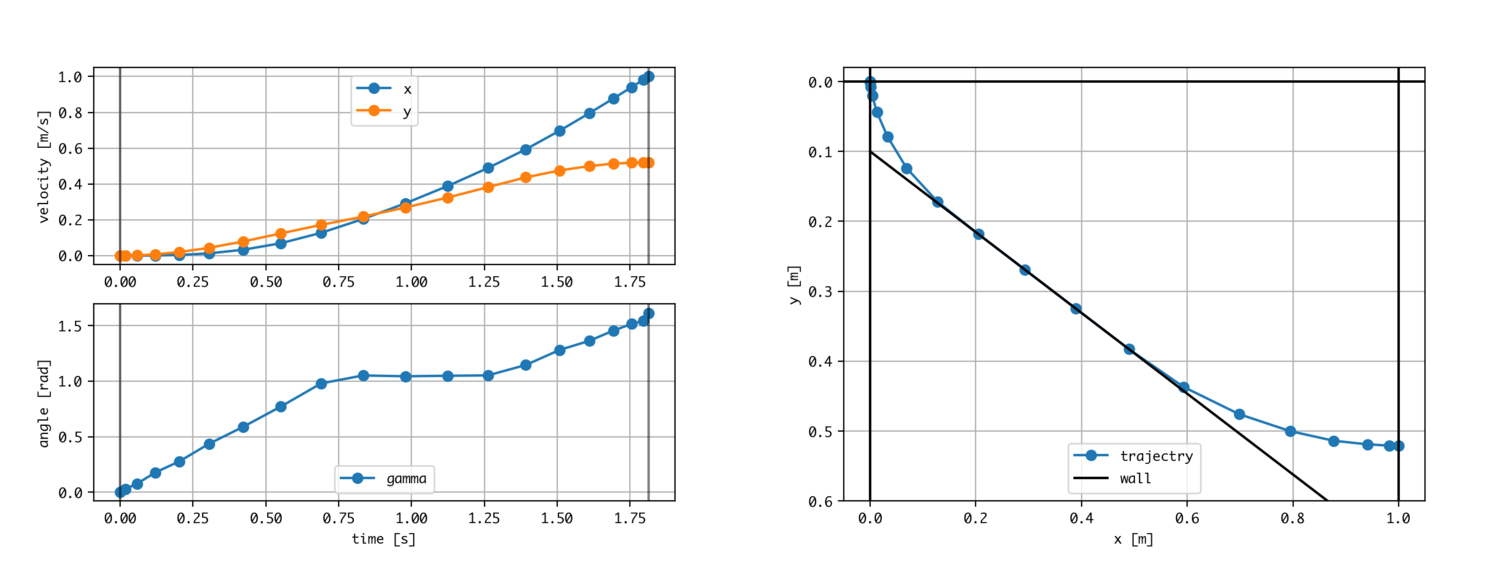
結果
壁という拘束条件に守りながら軌道を作っているのがわかります。
これは変分法で解く解析解とはびみょーーーに異なります。これは収束の閾値だったり分割点の数が足りないことによります。
東京−大阪間を摩擦と空気抵抗の無いトンネルで結ぶ問題
最速降下問題の実応用(?)として、東京−大阪間をイメージし、600kmの距離を重力加速度9.8m/s2で、摩擦と空気抵抗が無いとしてどんなトンネルを掘れば最速で到着するか計算してみます。
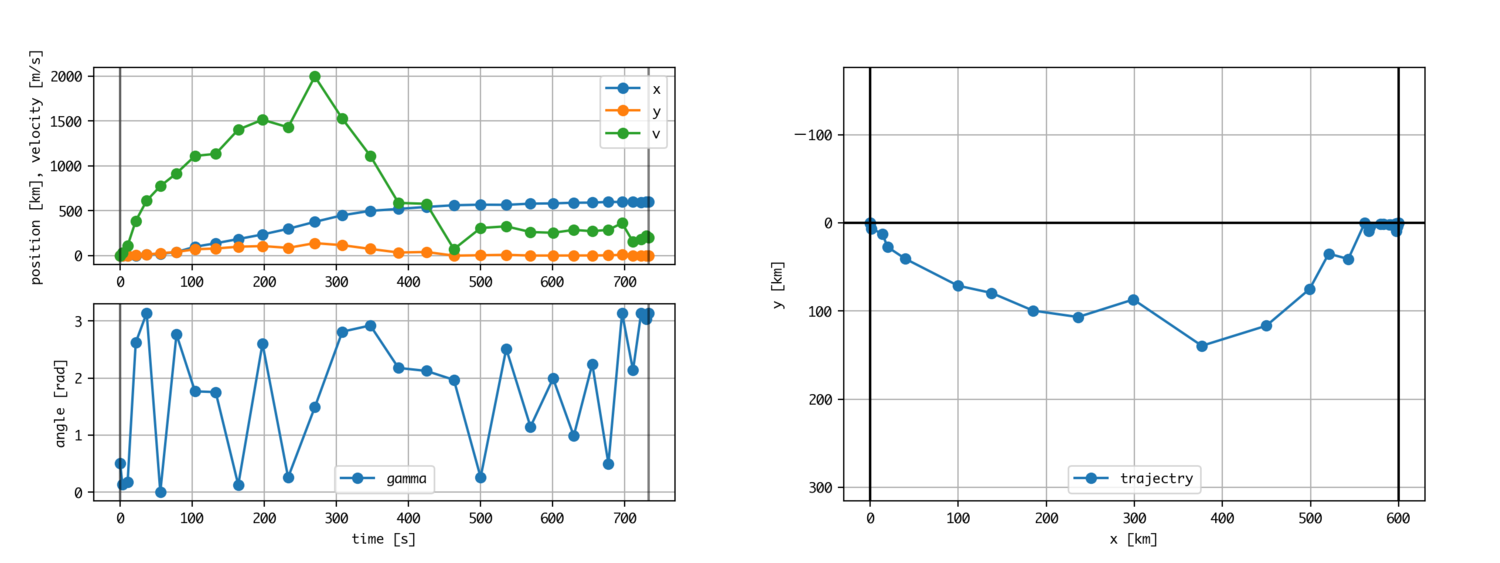
距離600kmに変更してそのまま計算してみます。
class Ball:
def __init__(self):
self.g = 9.8 # gravity [m/s2]
self.l = 600000 # goal [m]
self.h = 300000 # depth limit [m]
駄目でした。制御変数の値がバタバタしていてまともな結果になっていません。
何故か?これは内部で計算している変数に理由があります。
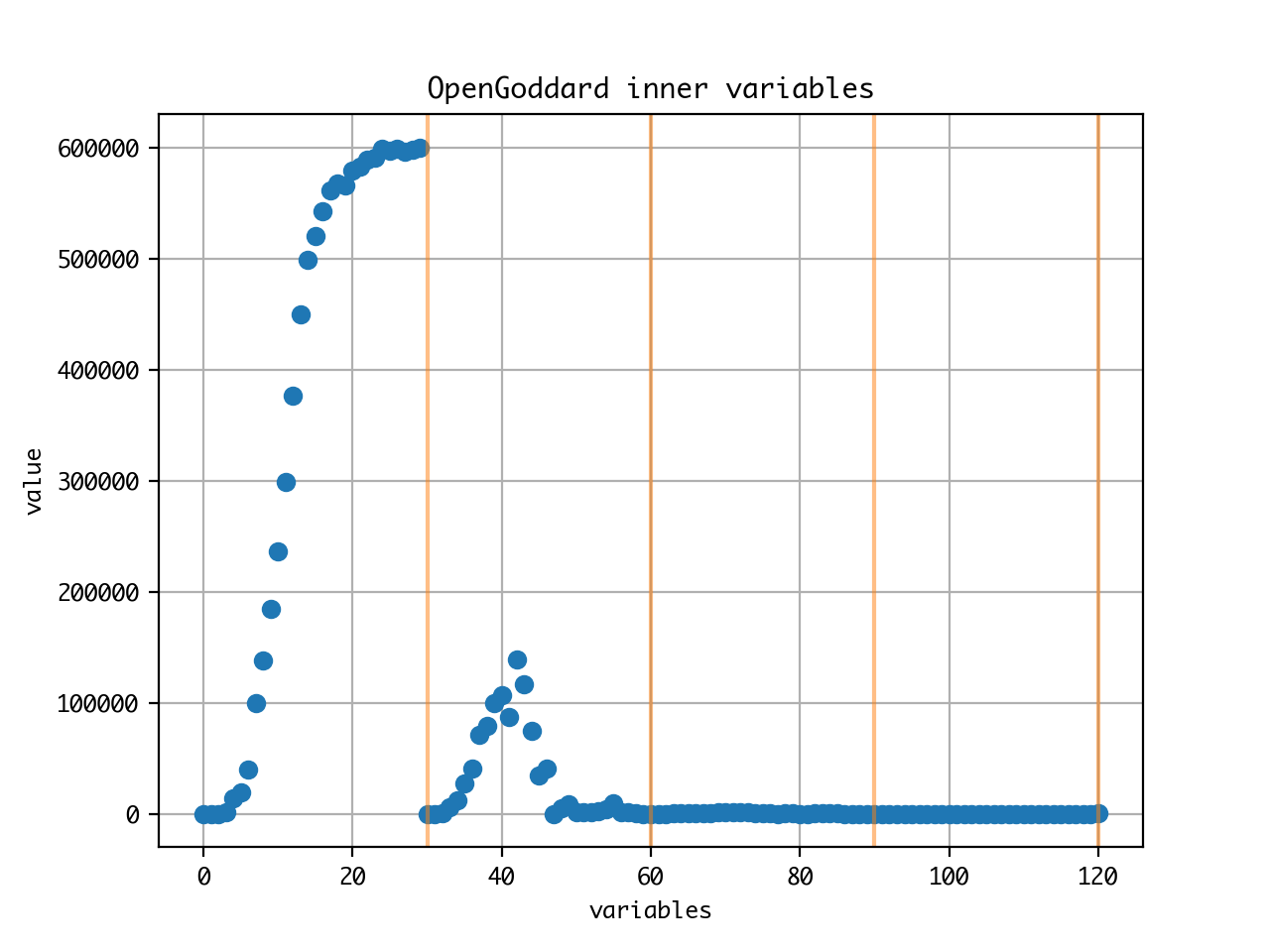
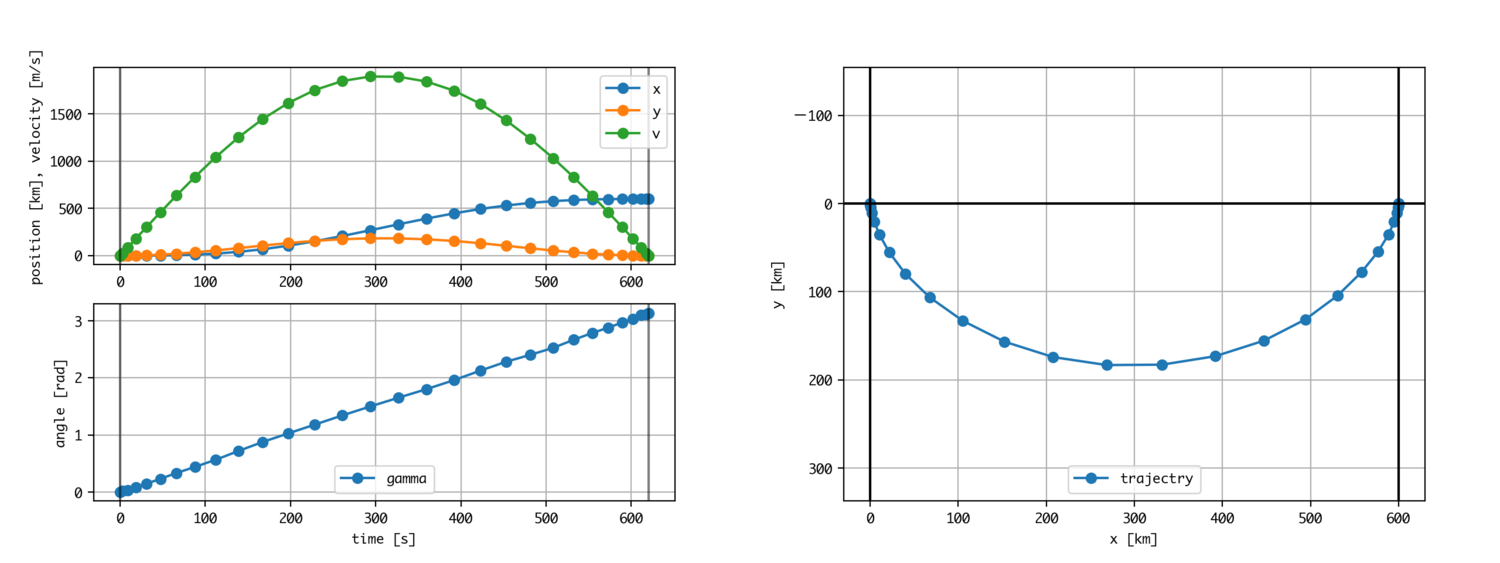
prob.plot()
実行後に上記のコマンドをipythonやjupyter notebook上ですると、OpenGoddard.optimizeのProblemインスタンスのplotメソッドが呼ばれ、最適化ソルバーに突っ込んでいる中身の変数の値が可視化できます。
左から順に状態変数、制御変数、時間(点)の意味になっています。
一番左のところがxの値です。値のオーダーは数十万です。一方vは数千、経路の角度θに至っては0〜3あたりの値になっています。
逐次二次計画法のソルバーはそれぞれの変数のオーダーが合っていないと機嫌を損ねます。
計算機は変数の意味を知らずに可視化されている内部の変数をいじって評価関数を最小化しようとしているのに評価関数に効きすぎる変数と効かなさすぎる変数があると、上手く行かないのが原因です。
したがって、変数のオーダーを揃える正規化を行います。状態変数、制御変数、時間のそれぞれをオーダーが揃うように設定していきます。変数はおおよそ−10から10に収まるようにすると良い、というのが目安です。
unit_x = 300000
unit_y = 100000
unit_t = 100
unit_v = unit_x / unit_t
prob.set_unit_states_all_section(0, unit_x)
prob.set_unit_states_all_section(1, unit_y)
prob.set_unit_states_all_section(2, unit_v)
prob.set_unit_controls_all_section(0, 1.0)
prob.set_unit_time(unit_t)
これで内部の変数は正規化されました。
これで解が出ます。
最大深さ183km、最大速度マッハ5.5(1893m/s)、時間にして10分20秒で到着。
このトンネルでは地下100kmぐらいまでほとんど自由落下することに耐える必要があり、また、人類これまで一番深く掘った穴が12kmらしいので、その10倍以上掘る必要があります。
うーん、残念、非現実的。