OpenGoddard使い方４-非線形最適制御・軌道生成のためのpythonライブラリ

https://github.com/istellartech/OpenGoddard
https://istellartech.github.io/OpenGoddard/

OpenGoddard使い方１
OpenGoddard使い方２
OpenGoddard使い方３
OpenGoddard使い方４←いまここ

今回は、最適化のための定石テクニックの一つを使った定式化と結果について。

低推力軌道遷移問題

小惑星探査機はやぶさにも搭載されたことで有名になったイオンエンジンなど電気推進の発展によって、例えば地球から他の惑星までロケットエンジンのような化学推進ではなく電気推進で行くということが多くなってきました。
化学推進での軌道遷移はホーマン軌道と呼ばれる軌道を取ることが必要エネルギー最小でいけるということが有名です。
ただし、これは十分な推力のあるエンジンのみで、低推力ではスパイラル軌道と呼ばれる軌道になってしまいます。
2地点間の軌道遷移の問題は多くは境界値問題として解いていく（ランベール問題という。ランベルト問題ともいう、Lambert's Problem）が、ここでは最適制御問題として扱って解いてみます。

元となる論文は以下のものです。

Ross, I. Michael, Qi Gong, and Pooya Sekhavat. "Low-thrust, high-accuracy trajectory optimization." Journal of Guidance, Control, and Dynamics 30.4 (2007): 921-933.
https://doi.org/10.2514/1.23181

運動方程式

\begin{align}
\dot{r} &= v_r \\
\dot{v_r} &= v_t^2 / r - 1 / r^2 + u_r \\
\dot{v_t} &= - v_r v_t / r + u_t
\end{align}

拘束条件

初期値と終端値をいれて、推力の大きさの制限を入れます。

|u_r| \leq 0.01 \\
|u_t| \leq 0.01 \\
0 < t_f < 55

評価関数

必要とする推力の時間合計の最小化を狙います。

J = \int_{t_0}^{t_f} |u_r| + |u_t| dt

絶対値の置き換え

絶対値の入った評価関数は滑らかでは無いので、数値解析の定石として、自由変数（補助変数とも）を使った置換を行います。
http://www.msi.co.jp/nuopt/download/introduction/module/technic.pdf

u = u_1 - u_2 \\
|u| = u_1 + u_2

これを考慮して、状態変数３つ（$r, v_r, v_t$）と制御変数４つ($u_{r1}, u_{r2}, u_{t1}, u_{t2}$)として記述していきます。

また、評価関数に積分項がある場合にはrunning_costに積分項の中身を指定します。

def running_cost(prob, obj):
    ur1 = prob.controls_all_section(0)
    ur2 = prob.controls_all_section(1)
    ut1 = prob.controls_all_section(2)
    ut2 = prob.controls_all_section(3)

    return (ur1 + ur2) + (ut1 + ut2)

prob.running_cost = running_cost

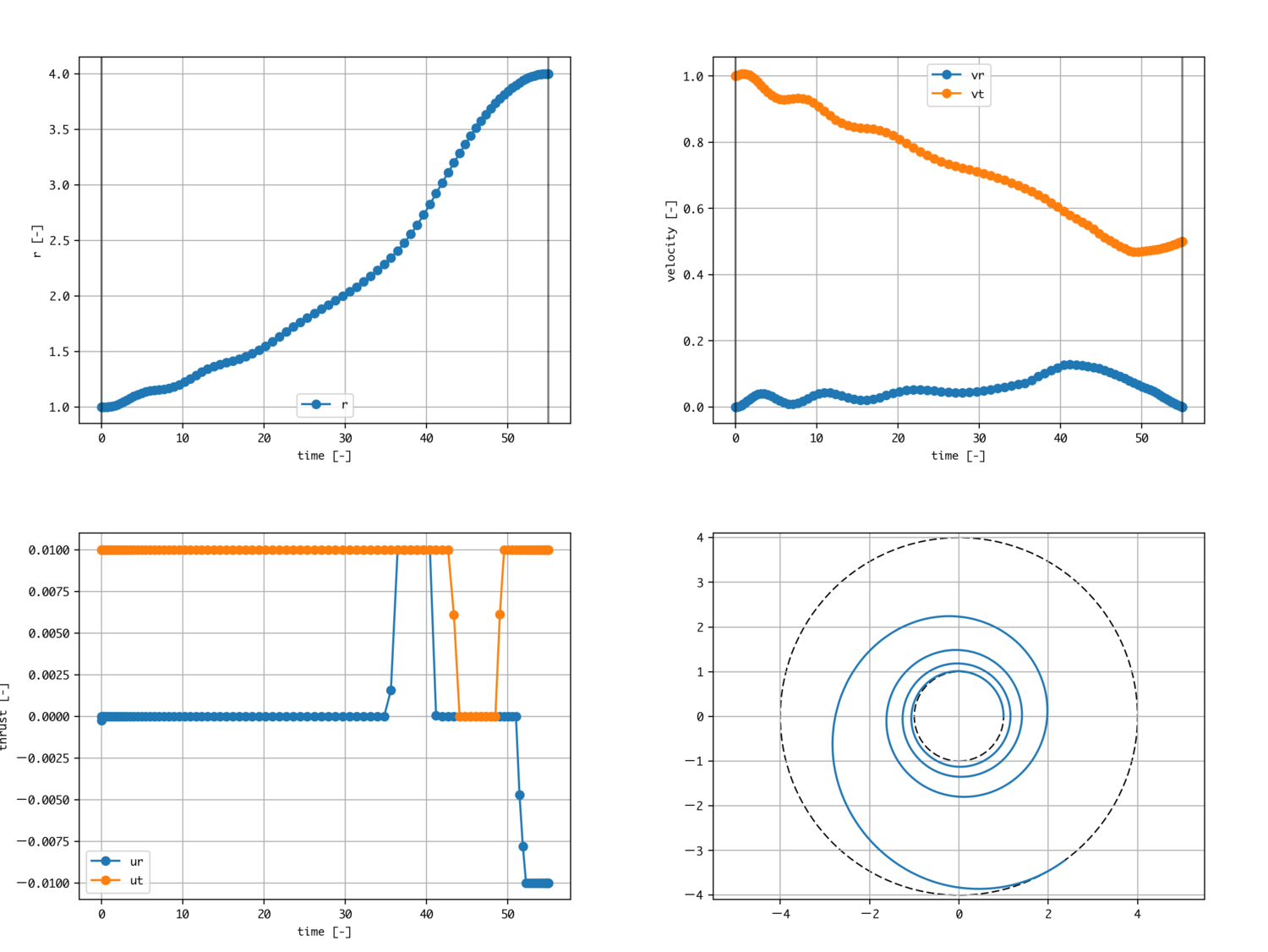
結果

制御変数であるuのグラフを見ると、人間には理解しづらい推力の履歴になることがわかります。
こんな難しい問題も、（ある程度の試行錯誤とノウハウは必要ですが）簡単に解くことが出来ます。

まとめ

以上のように、OpenGoddardを使うにあたって簡単な例から、注意点となりうるところを解説していきました。
簡単にまとめると以下の通りです。

• スケーリング - 変数の大きさのオーダーを揃えてあげる
• 区間更新 - knotを増やしたり減らしたり
• knotting method - 状態変数の非連続な部分の定義
• 絶対値など滑らかでないものの置換

あたりがノウハウで非直感的な部分として残っていますが、それでも簡単に非線形最適制御の解（軌道）を求めることができます。
数値解なので最適値であるという保証が無いことと、局所最適解であるというのが重要な注意点ではありますが、多くの実務では問題ないと思います。
是非、OpenGoddardを使ってみて下さい！

蛇足１

逐次二次計画法のソルバーでv1.0.0現在採用しているのがScipyのSLSQPというものですが、このソルバーの性能が大規模問題には向いていません。変数やnodeの数が多い問題では計算時間がかなりかかります。ココらへんは疎行列の特性を使った高級なソルバーを使うといいっぽいですが、未検証です。よく論文などに出ているのはSNOPTやIPOPTです。

蛇足２

今回説明したOpenGoddardの他にOpenTsiolkovskyというプログラムを公開しています。

• OpenGoddard(名前の由来） - 近代ロケットの父と呼ばれるアメリカのロバート・ゴダードさん
• OpenGoddard（中身) - 最適化問題を解くことにより軌道設計
• OpenTsiolkovsky(名前の由来) - 宇宙旅行の父と呼ばれるコンスタンチン・ツォルコフスキーさん
• OpenTsiolkovsky(中身) - ロケットの運動方程式から微分方程式を解いてロケットの軌道計算

この２つは逆問題と順問題という、一対となるソフトです。

元々作った理由はロケットの軌道生成だけれども、結果的にOpenGoddardはかなり汎用的なツールです。
大規模な最適制御問題は別のツールを使ったほうが良いかもしれませんが、簡単な計算であれば依存関係も少なくインストールも楽なので良いツールだと思います（熱い自画自賛）