https://github.com/istellartech/OpenGoddard
https://istellartech.github.io/OpenGoddard/
OpenGoddard使い方1
OpenGoddard使い方2←いまここ
OpenGoddard使い方3
OpenGoddard使い方4
Goddard問題(大気中のロケット最適上昇制御問題)
ロケット工学の中では古典的な問題である、大気中のロケット最適上昇するための最適推力制御の問題である、ゴダード問題を解いていきます。
詳細はexampleのファイルを見てください。
運動方程式
ロケットの運動を1次元(高さだけ)で考えます。ロケットエンジンでの推力と空気抵抗を考えて高度最大化を考えます。
T:推力
D:抗力(空気抵抗)
g:重力加速度
\begin{align}
\dot{h} &= v \\
\dot{v} &= \frac{T - D}{m} - g \\
\dot{m} &= - \frac{T}{c}
\end{align}
拘束条件
初期条件・終端値条件・状態変数と制御変数の上限下限を入力します。
評価関数
最小化したい値をreturnに入れる。ここでは、高度の最大化を目指したいので、符号に注意して下記の通りです。
J = -h
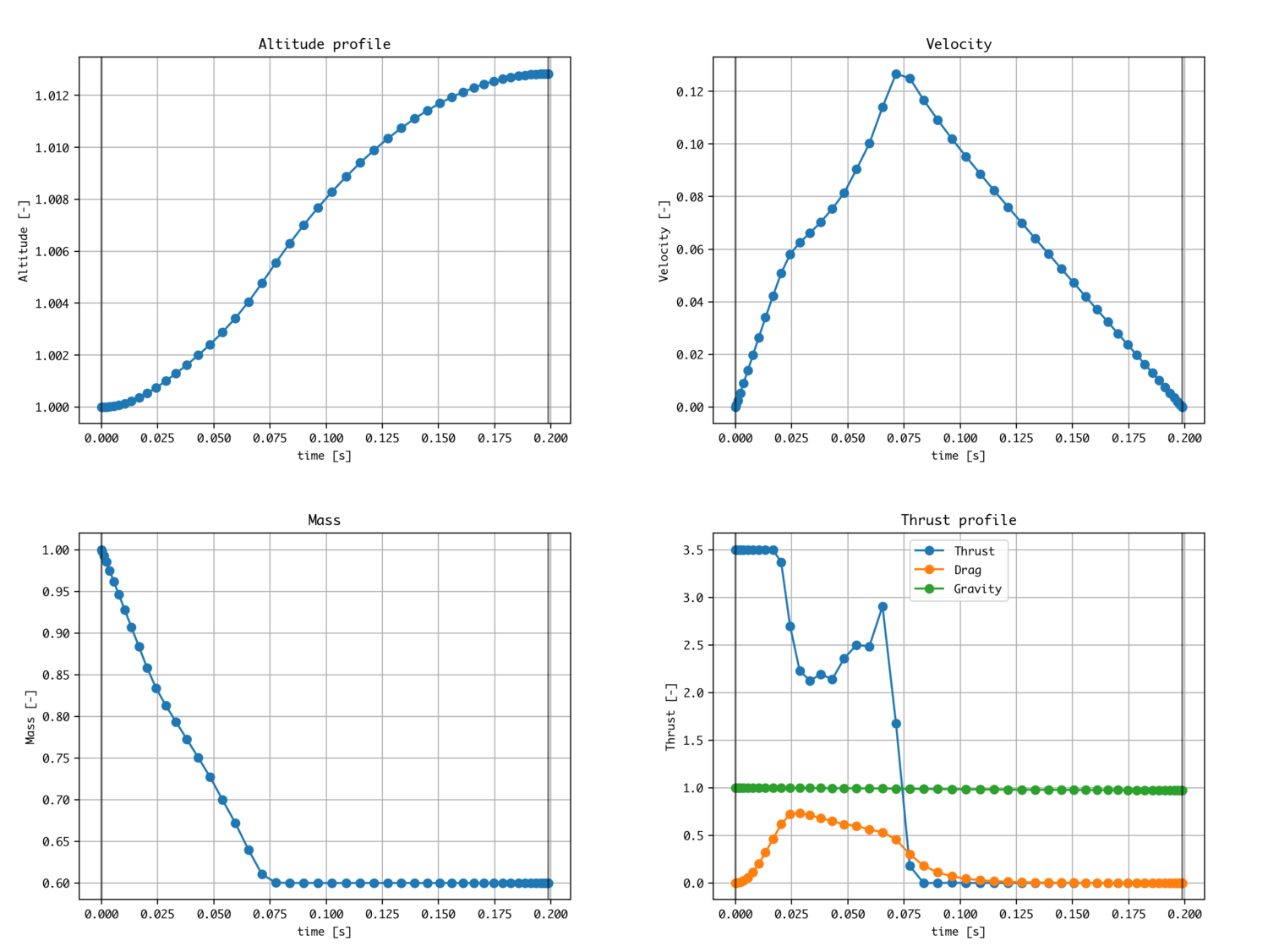
結果
最初はフルスロットルで、途中で推力を絞ってあげるのが良いという結果になりました。
これは、現象的には重力による減速を小さくするために、推力はなるべく大きい方がいい、という性質と、空気抵抗は小さいほうがいいから空気濃いところでは加速しすぎないほうがいいという性質の兼ね合いの結果です。
専門用語では重力損失と空力損失の合計の最小化と言えます。
実際のロケットでも同じようなことを実際考えられていて、固体燃料ロケットでは、推力を途中で良い感じに調整しています。
ゴダード問題の解は実利用されています!
最適化問題は世の中の役に立つ!すごい!
knotting method
OpenGoddardの中身である擬スペクトル法はすごいアルゴリズムですが、状態変数、制御変数が滑らかでない(微分可能ではない)ものは苦手です。制御変数が非連続に変わるものも若干苦手です。また絶対値なんかも得意じゃないです。
ゴダード問題で言うと、高度、速度、重量、推力が滑らかになるようにしか解いてくれません。
状態変数、制御変数をある特定の点で非連続でもで解を求める手法として、knotting methodというのを使います。
これは、非連続な部分で計算区間をわけてしまう方法です。
OpenGoddardでは簡単にknotting methodが使えるようになっています。
(世の中には自動的にknotting methodの区間を分けるアルゴリズムの最適化ソフトもあります・・・)
Goddard問題(knotあり)
Problemクラスに入れる値をリストで並べていきます。
time_init = [0.0, 0.1, 0.3]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]
また、区間ごとにどの運動方程式が適応されるのか指定し、状態変数が連続であるかどうかを指定します。
ここでは、制御変数だけが非連続に変化するという予測のもとにTrueを選択しています。ここのTrue/Falseと拘束条件は密接に関係するので注意して指定します。
Falseの場合は拘束条件(equality)にknot点で変数を固定しないと発散します。
prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [True]
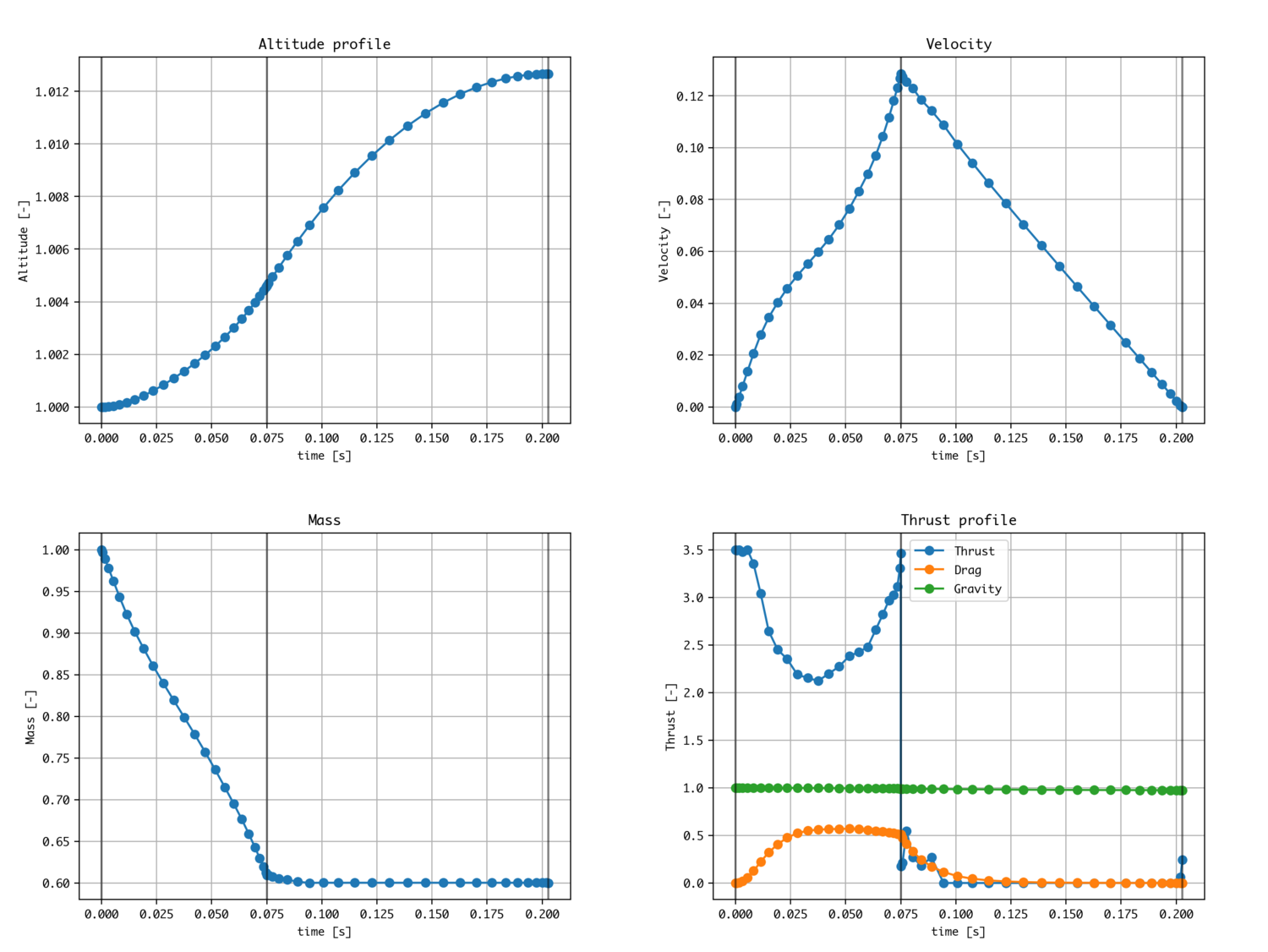
以上により、
knot有りは最高高度下がりました。。。あまり良い成果になりませんでした。
このようにknotting methodを使えば単純に良いということではありませんが、変数が非連続な問題も扱うことが出来るようになりました。