1. はじめに
大規模言語モデル(LLM; Large Language Model)の導入がビジネスや生活の中で進んできています。LLMを活用する際、LLMが事実と異なる出力をするハルシネーション(幻覚)と呼ばれる現象に悩まされる方も多いと思いますが、ハルシネーションを回避・低減する方法の研究も進んでいます(たとえば、L. Huang et al., 2023をご覧ください)。本記事では、LLMの回答の不確実性を定量化し、それをもとにハルシネーションを検出する手法を提案した、Google DeepMindによる論文 To Believe or Not to Believe Your LLM を簡単に紹介します。(LLMの概要や基礎的な理論についてはこちらの記事をご参照ください。)
以前の記事では、LLMの内部状態を解析することでハルシネーションを検出するLLM factoscopeという手法を提案した論文を紹介しましたが、今回ご紹介する論文では、LLMの回答の不確実性を情報理論の指標を使って定量化し、それをもとにハルシネーションを検出するという異なるアプローチを取っています。
2. 論文「To Believe or ~」の要点
この論文では、LLMにおける不確実性の定量化を試みています。具体的には、LLMの回答の不確実性をepistemicなもの(知識の欠如による)とaleatoricなもの(不可避なランダム性による)に分け、epistemicな不確実性が高い場合にモデルの出力が信頼できないことを検出する、情報理論に基づいた新しい指標を導入しています。また、クエリ(質問)と回答を繰り返して得られる回答の分布をもとにepistemicな不確実性を計算し、ハルシネーションを検出するアルゴリズムを提案しています。
2.1 epistemic/aleatoricな不確実性
- epistemicな不確実性
- 学習データやモデルのキャパシティが十分でないなどの理由で正解(事実や、言語における文法など)に関する知識が欠如してしまうことに起因する不確実性
- epistemicな不確実性が高いとき、ハルシネーションの発生が疑われる
- aleatoricな不確実性
- 同一のクエリに対して妥当な(正しい)回答が複数ある場合など、不可避なランダム性に起因する不確実性
epistemicな不確実性が小さいとき、LLMの回答は正解に近く、回答の信頼性が高いといえます。
回答の不確実性を定量化するヒューリスティックなアプローチは様々なものが検討されてきています(回答の対数尤度を検証する・エントロピーを推定する・アンサンブルを行う・conformal predictionを活用する、など)が、これらのアプローチは正解となる回答が1つのみ存在する場合しか適用できないという限界があります。正解となる回答が複数ある場合は(正解における)aleatoricな不確実性が高い訳ですが、単純にLLMの回答の不確実性を見積もる方法では、epistemicな不確実性が高いのか、aleatoricな不確実性が高いのかを見分けることができません。このことが、この論文における不確実性の定量化のモチベーションになっています。
3. epistemicな不確実性の定量化
3.1 カルバック・ライブラー情報量を用いた定量化
LLMの回答が正解からどの程度乖離しているかを測定する指標として、LLMの出力の確率分布 $\tilde{Q}$ と正解の確率分布 $\tilde{P}$ とのカルバック・ライブラー情報量 $D_{KL}(\tilde{Q}, \tilde{P})$ を導入しています。図1に示したイメージ図では、LLMの出力の確率分布 $\tilde{Q}$ と正解の確率分布 $\tilde{P}$ の乖離が大きく、ハルシネーションの発生が疑われます。
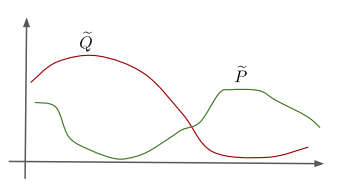
図1: ハルシネーションの発生が疑われる場合の、LLMの回答の確率分布 $\tilde Q$と正解の確率分布 $\tilde P$ のイメージ図(Yadkori et al., 2024 Figure 4を引用)
3.2 前提と計算方法の概要
LLMの出力の確率分布の算出に際しては、クエリに対する回答を得て、その回答とクエリをもとに次の回答を得て、さらにこれまで得られた回答とクエリをもとに次の回答を得る、という手続きを踏みます。そして、LLMの出力の確率分布は、クエリに対する回答が得られる確率、クエリと1つ目の回答のもとで2つ目の回答が得られる確率、クエリと2つ目までの回答をもとに3つ目の回答が得られる確率、…の積で表現されます。
クエリとこれまでの回答を含むプロンプトに対する回答が、これまでの回答の影響をあまり受けない場合、上記の方法で計算されるLLMの回答の確率分布は正解のものと近くなるはずです。これはLLMが自信をもって回答している状況と見做すことができます。一方で、これまでの回答が新しい回答へ与える影響が大きい場合、LLMの回答の確率分布は正解のものとは乖離したものとなります。これはLLMが回答に自信を持てない状況に該当するといえるでしょう。したがって、LLMの回答の確率分布と正解の確率分布の差異であるカルバック・ライブラー情報量は、aleatoricな不確実性の影響を受けず、epistemicな不確実性を定量化しているといえます。
また、$D_{KL}(\tilde{Q}, \tilde{P})$ は、正解の確率分布がこれまでの正解に依存しないという仮定の下で、$\tilde{Q}$ のみに依存し、回答の確率分布の相互情報量 $I(\tilde{Q})$ を下界に持つ、つまり
D_{KL}(\tilde{Q}, \tilde{P}) \geq I(\tilde{Q})
が成り立つことが示されています。図2に、相互情報量の計算方法を示します(証明や計算方法に関する詳細は文献をご参照ください)。

図2: 相互情報量の計算方法(Yadkori et al., 2024 Algorithm 1を引用)
4. ハルシネーションの検出アルゴリズム
この論文では、前節の相互情報量 $I(\tilde{Q})$ をもとに、スコアベースでハルシネーションを検出するアルゴリズムを提案しています。
提案されている手法は、クエリ $x$ のもとで得られる回答の確率分布の相互情報量を、ハルシネーションが発生しているかの確信度を表すスコアとして活用しています。具体的には、
- 相互情報量が閾値 $\lambda$ 以上の場合 ⇒ ハルシネーションが発生している
- 相互情報量が閾値 $\lambda$ 未満の場合 ⇒ ハルシネーションが発生していない
と見做します。(閾値 $\lambda$ は、ホールドアウトデータを用いてチューニングするパラメータです。)
5. 評価
この論文では、LLMとしてGemini 1.0 Pro、データセットとしてTriviaQA, AmbigQA, WordNetを使い、ハルシネーションの検出精度を検証しています。
図3は、ハルシネーション検出の精度評価結果を示しており、提案手法(M.I. score)は、ベースライン手法(T0 score, S.V. score, S.E. score)と同程度もしくはより高い精度を達成していることがわかります。
詳しく見てみると、ほとんどが正答が1つであるクエリ/回答から構成されるデータセット TriviaQA, AmbigQA に対する評価(図a,b)では、回答の尤度にもとづくナイーブな手法(T0 score, S.V. score)よりも精度がよく、不確実性の指標として回答のエントロピーを使用している手法(S.E. score)と同程度の精度を示していることがわかります。また、正答が1つであるクエリ/回答と、正答が複数あるクエリ/回答をどちらも含むデータセット TriviaQA+WordNet, AmbigQA+WordNet に対する評価(図c, d)では、ベースライン手法(S.E. score)よりも良好な性能を示していることがわかります。
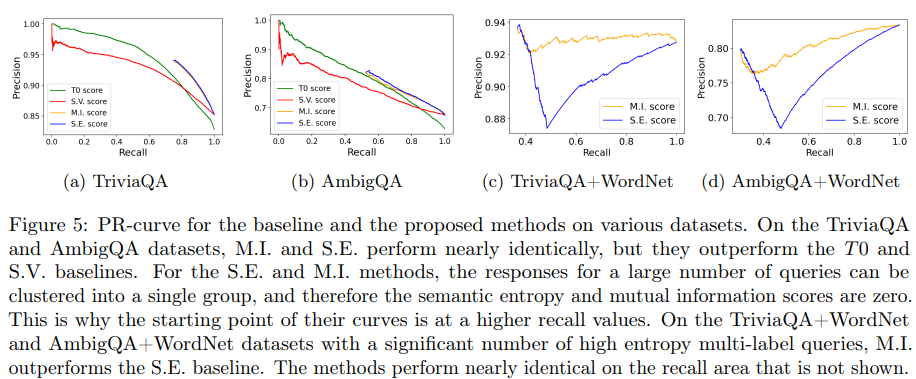
図3: ハルシネーションの検出精度を示すPrecision-Recall曲線(Yadkori et al., 2024 Figure 5を引用)
6. まとめ
この記事では、LLMの回答の不確実性を定量化する手法を提案した論文を簡単に紹介しました。ハルシネーションの回避・低減に取り組まれている方や、LLMに興味をお持ちの方の参考になれば幸いです。
7. 参考文献
[1] Yadkori et al., 2024, To Believe or Not to Believe Your LLM