はじめに
以前、「機械学習の分類」で取り上げたアルゴリズムについて、その理論とpythonでの実装、scikit-learnを使った分析についてステップバイステップで学習していく。個人の学習用として書いてるので間違いなんかは大目に見て欲しいと思います。
今回は、線形回帰編のまとめとしてガウシアンカーネルを使った線形近似と、過学習やそれを抑えるL1正則化(Lasso)、L2正則化(Ridge)についてまとめてみようと思う。
今回参考にしたのは以下のサイト。ありがとうございます。
- 線形な手法とカーネル法(1. 回帰分析)
- リッジ回帰とラッソ回帰の理論と実装を初めから丁寧に
- 正則化項(LASSO)を理解する
- ラッソ回帰を実装してみよう
- scikit-learnで線形モデルとカーネルモデルの回帰分析をやってみた - イラストで学ぶ機会学習
カーネル近似について
以前、線形回帰の一般化について書いた時に、「基底関数はなんでもよい」と書いた。現実の回帰でも常に直線で近似できるとは限らず、多項式や三角関数のようなクネクネした近似というのも必要になってくる。
例えば$y=-xsin(x)$にノイズを乗せた$y=-xsin(x)+\epsilon$について考える、
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots()
t = np.linspace(0, 2*np.pi, 100)
y1 = - t * np.sin(t)
n=40
np.random.seed(seed=2020)
x = 2*np.pi * np.random.rand(n)
y2 = - x * np.sin(x) + 0.4 * np.random.normal(loc=0.0, scale=1.0, size=n)
ax.scatter(x, y2, color='blue', label="sample(with noise)")
ax.plot(t, y1, color='green', label="-x * sin(x)")
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=11)
plt.show()

青い点がノイズを乗せたサンプルで、緑の実線が想定する関数を示している。ノイズは乱数で加えたが、毎回同じ結果になるように乱数のシード値は固定した。
今回は目的関数がわかっているのでよいが、サンプルが多項式なのかそれとも別な関数なのかはわからない状態から推定しなければならない。
ガウスカーネルついて
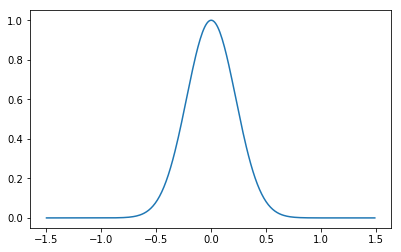
ガウスカーネルは次のように定義されます。
k(\boldsymbol{x}, \boldsymbol{x'})=\exp(-\beta||\boldsymbol{x}-\boldsymbol{x'}||^2)
$||\boldsymbol{x}-\boldsymbol{x'}||^2$はベクトル同士の距離で、$\sqrt{\sum_{j=1}^{n}(x_j-x'_j)^2} $とも表されます。
この関数は以下のような形をしており、この関数の中心を移動したり大きさを変えることで目的のデータ列に回帰させます。
ガウスカーネルを使った線形回帰
今、目的の関数を
f({\bf x})=\sum_{i=1}^{N} \alpha k({\bf x}^{(i)}, {\bf x}')
とする。標本の値を$\hat{y}$とすると、
\hat{y} =
\left(\begin{matrix}
k({\bf x}^{(1)}, {\bf x}) & k({\bf x}^{(2)}, {\bf x}) & \cdots & k({\bf x}^{(N)}, {\bf x})
\end{matrix}\right)
\left(\begin{matrix}
\alpha_0 \\
\alpha_1 \\
\vdots \\
\alpha_N
\end{matrix}\right)
となり、
{\bf y} =
\left(\begin{matrix}
y^{(1)} \\
y^{(2)} \\
\vdots \\
y^{(N)}
\end{matrix}\right)
,\;
K=\left(\begin{matrix}
k({\bf x}^{(1)}, {\bf x}^{(1)}) & k({\bf x}^{(2)}, {\bf x}^{(1)}) & \cdots & k({\bf x}^{(N)}, {\bf x}^{(1)}) \\
k({\bf x}^{(1)}, {\bf x}^{(2)}) & k({\bf x}^{(2)}, {\bf x}^{(2)}) & & \vdots \\
\vdots & & \ddots & \vdots \\
k({\bf x}^{(1)}, {\bf x}^{(N)}) & \cdots & \cdots & k({\bf x}^{(N)}, {\bf x}^{(N)})
\end{matrix}\right)
,\;
{\bf \alpha}
=
\left(\begin{matrix}
\alpha^{(1)} \\
\alpha^{(2)} \\
\vdots \\
\alpha^{(N)}
\end{matrix}\right)
という風に展開される(このへんコピペですすいません)。ここで$K$をグラム行列と呼ぶ。$f({\bf x})$と$\hat{y}$の二乗誤差$L$は
L=({\bf y}- K {\bf \alpha})^{\mathrm{T}}({\bf y}- K {\bf \alpha})
となり、これを$\alpha$について解くと、$${\bf \alpha} = (K^{\mathrm{T}}K)^{-1}K^{\mathrm{T}}{\bf y} = K^{-1}{\bf y}$$となる。つまり、グラム行列の逆行列が計算できれば$\alpha$を求めることが可能ということになる。観測サンプル数が多すぎる場合、この逆行列を求めることが大変になるので別の方法を選ぶ必要がある。
pythonでの実装
上の式をそのまま使ってKernelRegressionクラスを実装した。
class KernelRegression: #正則化なし
def __init__(self, beta=1):
self.alpha = np.array([])
self.beta = beta
def _kernel(self, xi, xj):
return np.exp(- self.beta * np.sum((xi - xj)**2))
def gram_matrix(self, X):
N = X.shape[0]
K = np.zeros((N, N))
for i in range(N):
for j in range(N):
K[i][j] = self._kernel(X[i], X[j])
K[j][i] = K[i][j]
return K
def fit(self, X, Y):
K = self.gram_matrix(X)
self.alpha = np.linalg.inv(K)@Y
def predict(self, X, x):
Y = 0
for i in range(len(X)):
Y += self.alpha[i] * self._kernel(X[i], x)
return Y
最初のサンプルを使って近似させてみる。
model = KernelRegression(beta=20)
model.fit(x, y2)
xp = np.linspace(0, 2*np.pi, 100)
yp = np.zeros(len(xp))
for i in range(len(xp)):
yp[i] = model.predict(x, xp[i])
fig, ax = plt.subplots()
plt.ylim(-3,6)
ax.plot(xp, yp, color='purple', label="estimate curve")
ax.scatter(x, y2, color='blue', label="sample(with noise)")
ax.plot(t, y1, color='green', label="-x*sin(x)")
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=11)
plt.show()

確かに与えられたサンプル上を通っているみたいですがグチャグチャです。緑の曲線とは全然違いますね。
過学習(overfitting)について
上のように学習の結果が教師データに対して忠実だが、現実とかけ離れてしまうことを**過学習(overfitting)**と言います。数学のテストで、教科書と同じ問題が出れば解けるけどちょっとアレンジされるととたんに解けなくなるのと似ているでしょうか。
過学習されたモデルのことを汎化性能がよくないとも言います。予測精度が低い状態です。これを防ぐために、正則化という概念が必要になります。
正則化(regularization)
上の例では、与えられたサンプルの点を無理やり通すために、パラメータ$\bf{\alpha}$が極端に大きくなっていることが原因で激しく暴れる曲線になってしまっています。あとは、データ数が極端に少なかったり、変数が多い場合にこうなってしまうことが多いようです。
これを防ぐためには、$\alpha$を求める際に、カーネル回帰の二乗誤差に正則化項を加えることで$\alpha$の範囲を制限することで実現できます。機械学習ではL1正則化(Lasso)とL2正則化(Ridge)が有名です。両者をミックスさせるとElasticNet正則化と呼ばれます。
L2正則化
L1ではなくL2から始めます。
先ほど$\alpha$を求めた際に目的関数とサンプルの二乗誤差を$L$とおきましたが、$\lambda||{\bf \alpha}||_2^2$を加えた
L=({\bf y}- K {\bf \alpha})^{\mathrm{T}}({\bf y}- K {\bf \alpha})+\lambda||{\bf \alpha}||_2^2
を最適化します。$\lambda$が大きいほど$\alpha$が制限されるため、よりおとなしい(?)曲線になります。これを$\alpha$で偏微分して0とおき、$\alpha$について解くと、
{\bf \alpha} = (K+\lambda I_N)^{-1}{\bf y}
となります。これはグラム行列に単位行列を足して逆行列を計算するだけでよいので変更は簡単ですね。
pythonでの実装
先ほどのKernelRegressionクラスの$\alpha$を求める部分を若干変更しました。あとはほぼ同じです。
class KernelRegression: # L2正則化
def __init__(self, beta=1, lam=0.5):
self.alpha = np.array([])
self.beta = beta
self.lam = lam
def _kernel(self, xi, xj):
return np.exp(- self.beta * np.sum((xi - xj)**2))
def gram_matrix(self, X):
N = X.shape[0]
K = np.zeros((N, N))
for i in range(N):
for j in range(N):
K[i][j] = self._kernel(X[i], X[j])
K[j][i] = K[i][j]
return K
def fit(self, X, Y):
K = self.gram_matrix(X)
self.alpha = np.linalg.inv(K + self.lam * np.eye(X.shape[0]))@Y
def predict(self, X, x):
Y = 0
for i in range(len(X)):
Y += self.alpha[i] * self._kernel(X[i], x)
return Y
正則化しなかった場合と同じサンプルを使って近似してみます。$\beta$や$\lambda$の数値は適当に決めました。
model = KernelRegression(beta=0.3, lam=0.1)
model.fit(x, y2)
xp = np.linspace(0, 2*np.pi, 100)
yp = np.zeros(len(xp))
for i in range(len(xp)):
yp[i] = model.predict(x, xp[i])
fig, ax = plt.subplots()
plt.ylim(-3,6)
ax.plot(xp, yp, color='purple', label="estimate curve")
ax.scatter(x, y2, color='blue', label="sample(with noise)")
ax.plot(t, y1, color='green', label="-x*sin(x)")
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=11)
plt.show()

今回は見事に一致しました。実際は表示している範囲外では形が変わってしまうんですが、特定の範囲においてはかなり近い近似曲線がひけることがご理解いただけたと思います。
$\beta$や$\lambda$はハイパーパラメータと呼ばれ、これらを少しずつ変えて損失関数の値を最小化するという最適化も実際には必要になりますね。
L1正則化
L2正則化では、正則化項として、$\lambda ||{\bf \alpha}||^2_{2} $を加えましたが、L2正則化では正則化項として$\lambda||{\bf \alpha}||_1$を加えます。
L1正則化では正則化項が微分できないため、解を求めるのは少し複雑です。scikit-learnでは座標降下法(Coordinate Descent)という手法で実装されているみたいですが、私がまだ理解できていないので、本稿では素直にscikit-learnを使いたいと思います。
L1正則化は、パラメータ$\alpha$のかなりの部分を0にすることができ(スパースな解を得る)、不要なパラメータを削ることに役立ちます。
pythonでの実装
素直にscikit-learnで実装してみます。
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Lasso
kx = rbf_kernel(x.reshape(-1,1), x.reshape(-1,1))
KX = rbf_kernel(xp.reshape(-1,1), x.reshape(-1,1))
clf = Lasso(alpha=0.01, max_iter=10000)
clf.fit(kx, y2)
yp = clf.predict(KX)
fig, ax = plt.subplots()
plt.ylim(-3,6)
ax.plot(xp, yp, color='purple', label="estimate curve")
ax.scatter(x, y2, color='blue', label="sample(with noise)")
ax.plot(t, y1, color='green', label="-x*sin(x)")
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=11)
plt.show()
print("coef: ", clf.coef_)
coef: [-0. 0. 0. -0. -0.79703436 -0.
-0. -0. 0. -0. -0. 3.35731837
0. -0. -0.77644607 0. -0. 0.
-0. -0.19590705 0. -0. 0. -0.
0. 0. -0. -0. -0. 0.
-0. 0. -0. -0. 0. 0.58052561
0.3688375 0. -0. 1.75380012]

こちらも元の関数にだいぶ近似していますね。また、パラメータ(coef)もかなりの部分が0になっているのも確認できます。
Elasticnet
L1正則化とL2正則化はどちらも損失関数に正則化項を加えていますが、それぞれ独立に考えることができ、どちらをどれくらい採用するか決めることができ、これをElasticNetと呼びます。実際、scikit-learnの実装ではElasticNetのパラメータを変えたものをLassoとRidgeとして関数定義していました。
まとめ
線形回帰における基底関数は任意の関数を選ぶことができる。ガウシアンカーネル(に限らない)は、自由度が高く過学習しがちなのでL1正則化やL2正則化によって制限を加えることで、より汎化性能の高い回帰モデルを作ることができる。
数回にわたって回帰シリーズについてまとめてみたが、scikit-learnのチートシートにおけるRegressionの内容はだいたい理解できるようになったのではないだろうか。
割と適当にまとめたので、ツッコミは歓迎します。