LASSOについて
はじめに、線形回帰モデルの予測値$\hat {y}$を
\hat {y} = Xa
*$X:$ 観測データの集合行列 (詳細は前回記事参照) $a:$パラメータ
で表した場合、観測値と予測値の二乗誤差関数$R(a)$は下記式で定義される。
R(a)=||y-Xa||^2
正則化の概要については前回記事で記載した。
$R(a)$に$L_1$正則化項を加えて
R(a)=||y-Xa||^2+\lambda||a||\;\;\;\;(||a||=\sum _{ i=1 }^{ d }{ a_i } )
とすることを$L_1$正則化と言う。
次元圧縮について
LASSOはleast absolute shrinkage and selection operator の略であり、shrinkageが意味する通り、次元圧縮(変数$a$のうちできるだけ少ない変数を使って$y$を予測)が$L_1$正則化の目的である。
$L_1$正則化がない場合、$a$の算出は下記の最小化問題と等価。
\min _{ a }{\;\parallel y-Xa\parallel^2 }
ここに、$L_1$正則項を加えることは、下記の制約条件を加えたことになる。
||a||\le r
$d=2$ の場合、$a_1+a_2\le r$なので、$a_1,a_2$の取り得る値は四角の範囲内に制限される。
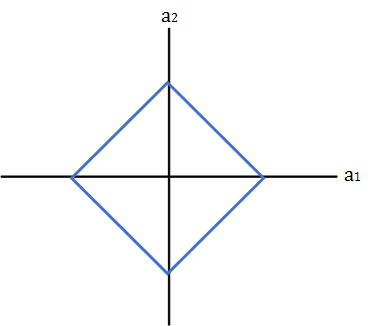
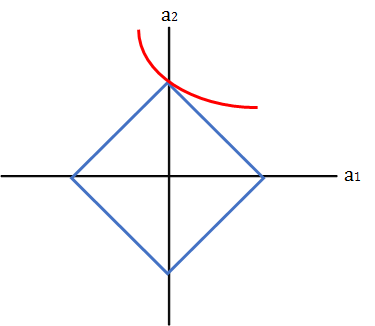
最小二乗解が赤線で求められる場合、$a_2=0$となり、次元が一つ減ることになる。
*$L_2$正則化の場合、制約条件は $||a||^2\le r $ なので、取り得る値は円形の範囲に制限される。
*L2正則化とは違い、L1正則化では|w|がw=0で微分できない。
L2正則化のように簡単に計算できず、数値的に求める必要がある。
1.求めてみる
ここでは、数学的な証明は割愛し、L1正則化の効果の確認に焦点を当てる。
なんで、可能な限りscikit-learnのライブラリを使用した。
データセットは、diabetes(糖尿病患者の検査数値と 1 年後の疾患進行状況)を使用。
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn import linear_model
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
alpha = [10, 1, 0, 0.1]
for a in alpha:
clf = linear_model.Lasso(alpha=a)
clf.fit(X_train, y_train)
y_true, y_pred = y_test, clf.predict(X_test)
print 'alpha=%.1f' % a, clf.coef_
print 'mse=(alpha%.1f):' % a, mean_squared_error(y_true, y_pred)
2.結果の確認
正則化パラメータは、[10, 1, 0, 0.1]で検証。(0 は正則化なし)
alpha=10.0 [ 0. 0. 0. 0. 0. 0. -0. 0. 0. 0.]
mse(alpha=10.0): 5101.49352133
alpha=1.0 [ 0. 0. 407.69646929 0. 0. 0.
-0. 0. 371.10978846 0. ]
mse(alpha=1.0): 3541.56574584
alpha=0.0 [ -52.46990773 -193.51064549 579.48277627 272.46404224 -504.7240054
241.68441227 -69.73619165 86.62018318 721.95579923 26.77887028]
mse(alpha=0.0): 3097.146139
alpha=0.1 [ -0. -119.31680615 571.71193009 213.44348648 -15.6273867
-64.57692007 -241.80314296 0. 526.21404185 0. ]
mse(alpha=0.1): 3124.40845263
正則化パラメータ10の場合、全ての値が0になっている。
また、誤差値も大きい。(正則化が厳しすぎる。)
一方、0.1の場合、3変数が0になっているのが分かる。
また、誤差の値も正則化なしと比べても大きく変化はない。
3.適切なパラメータの決定
LassoCVがクロスバリデーションによって最適な正則化項を見つけてくれる。
clf = linear_model.LassoCV(n_alphas=20)
clf.fit(X_train, y_train)
y_true, y_pred = y_test, clf.predict(X_test)
print 'alpha', clf.alpha_
print 'coef:', clf.coef_
print 'mse:', mean_squared_error(y_true, y_pred)
>> alpha 0.030105986244
>> coef: [ -31.61627977 -168.7080637 579.42526996 250.86866705 -152.36439422
-0. -230.85041776 0. 598.27973612 15.81230894]
>> mse: 3120.72065558
適切なモデルの選択は、AIC(モデル選択基準値)等を基準として判断すべき。
AICについても、どっかで実装しながら理解を深めたい。。