線形回帰を理解する。
機械学習の勉強本の導入部として紹介されることの多いのが、「線形回帰」だ。
(都市の人口や駅からの距離などの要素からその地価を予想するなどのやつ。)
主に下記の流れで紹介されることが多い。
- 予測とは
- モデルの作り方
- 誤差について
- 過学習
- 正則化
scikit-learnなどのライブラリを使用すると、データセットから正則化までやってくれるが、ここでは、自分で(計算過程でライブラリは使うが)行列式を計算して最小二乗法による推測を行い、知識の定着を図る。
平均二乗誤差からパラメータを求める。
実際の観測値$y$とモデルによる予測値$f(x,a)$の差は平均二乗誤差として下記のように定義される。
($x$は回帰式における各説明変数の値(都市の人口や駅からの距離)、$y$は目的変数の値(地価)を指す。)
E(a)= \frac{1}{n} \sum_i^n ( y^{(i)} -f( x^{(i)},a ))^{2}
個々の観測データ$x$,$y$を行列表現でまとめると、
E(a)= \frac{1}{n} \parallel y-Xa \parallel ^{2} = \frac{1}{n} (y-Xa)^{T} (y-Xa)
となる。
追記(2017/09/30):
$y$は個々の観測値を縦に並べたベクトル
($y^T$とした場合は横ベクトルを指す。)
ちなみに、観測値$x$の集合$X$の行列は、目的変数が3個、データの数が$n$個の場合
\begin{bmatrix} x_{1}^{(1)} & x_{2}^{(1)} & x_{3}^{(1)} \\x_{1}^{(2)} & x_{2}^{(2)} & x_{3}^{(2)} \\ \vdots&\vdots&\vdots \\x_{1}^{(n)} & x_{2}^{(n)} & x_{3}^{(n)} \end{bmatrix}
のような形をとる。(行はデータ数、列は説明変数の数)
*但し、線形回帰を行う際、バイアス(誤差)を含める場合、下記のように一列目を1の列を追加する。(必ずしも1である必要はない。)
\begin{bmatrix} 1& x_{1}^{(1)} & x_{2}^{(1)} & x_{3}^{(1)} \\ 1& x_{1}^{(2)} & x_{2}^{(2)} & x_{3}^{(2)} \\ \vdots& \vdots&\vdots&\vdots \\ 1& x_{1}^{(n)} & x_{2}^{(n)} & x_{3}^{(n)} \end{bmatrix}
誤差を最小化するための$a$を求めるので、誤差関数を$a$の各要素で微分する。
E(a)= \frac{1}{n}( y^{T}-X^{T}a^{T})(y-Xa)= \frac{1}{n}( y^{T}y-y^{T}Xa-X^{T}a^{T}y+X^{T}a^{T}Xa)
\frac{ \partial E(a)}{ \partial a}= \frac{1}{n}(-2X^{T}y+2X^{T}Xa)= -\frac{2}{n} X^{T}(y-Xa)=0
a=(X^{T}X)^{-1}X^{T}y
*行列の微分に関する補足
\frac{ \partial X^{T}a}{ \partial a}=X , \frac{ \partial a^{T}Xa}{ \partial a}=2Xa
追記(2017/09/30):
ベクトルによる微分の参考:正規方程式の導出と計算例
上で求めた$a$によって、モデルを作るための最適なパラメータが求められる。
実際に書いてみる。
1.データの作成
まず、最もシンプルな目的変数が1つの例
sklearnのdatasetsから回帰に適したサンプルデータを作る。
import numpy as np
from sklearn import datasets
np.random.seed(0)
sample_size = 50
noise_size = 10
dim = 1
data = datasets.make_regression(sample_size, dim, noise=noise_size)
ones = np.ones(sample_size).reshape(sample_size, 1)
feature = np.array(data[0])
X = np.hstack((ones, feature))
y = np.array(data[1])
誤差(切片)も求めるため、全てが1の列を追加している。
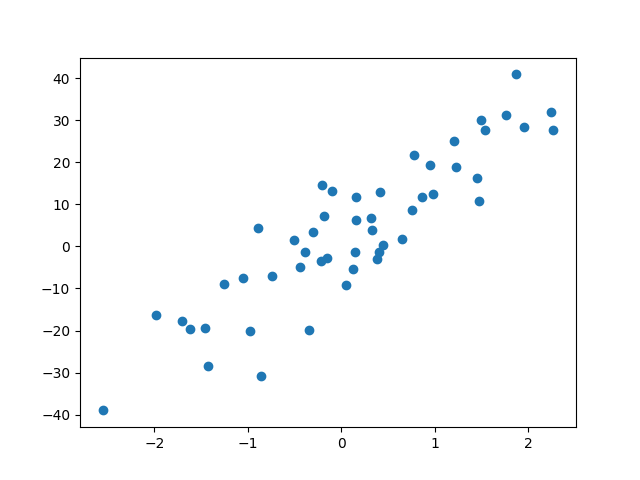
表示するとこんな感じ。(ノイズ付きの良さげな分布になっている。)
2.パラメータの算出
最小二乗解を求める。
XTX = np.dot(X.T, X)
XTX_inv = np.linalg.inv(XTX)
a = np.dot(XTX_inv, np.dot(X.T, y))
# [ 1.714 13.92 ]
ノイズが小さいので、誤差も小さくなっていることが分かる。
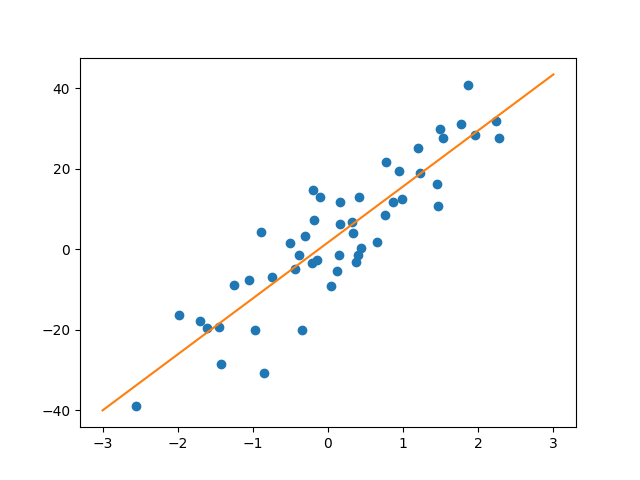
3.モデルを図示
linex = np.linspace(-3, 3, 1000)
f = lambda x: a[0] + a[1]*x
liney = f(linex)
plt.plot(linex, liney)
plt.show()
4.結果の確認
最後に、scikit-learnと値が一致することを確認する。
ライブラリを使った場合、これだけで済む。
from sklearn import datasets, linear_model
lin = linear_model.LinearRegression()
lin.fit(data[0], data[1])
print lin.intercept_, lin.coef_
# 1.71369654235 [ 13.92]
以上。次は、過学習と正則化についてまとめたい。