はじめに
- 前回の記事で重回帰分析の導入をしてみたので、今回はその続きということで、2つ同時にやってみたいと思います。
- ベクトルの微分公式については下記のブログが参考になります。
- もしこの記事がお役に立てた時はQiitaのイイねボタンを押していただけると励みになります。
参考記事
重回帰分析
リッジ回帰について考える際に、重回帰分析の理解はマストになるのでここでも見ていこうと思います。式変形については、前回の記事で詳しく導入したので少しだけ端折っていきます。
準備
- 説明変数$x_1, x_2, x_3, \cdots, x_m$を$\boldsymbol{x}$($x$のベクトル)とする
- 予測値を$\hat{y}$とする($\hat{y}$はスカラー)
- 回帰係数を$w_1, w_2, w_3, \cdots, w_m$を$\boldsymbol{w}$($w$のベクトル)とする
この時、目的変数は以下の式で表すことができます。
$$\hat{y}=w_1x_1 + w_2x_2 + \cdots + w_mx_m$$
この式に切片を加えるのですが、切片については$w_0x_0$と表します。
$$\hat{y}= w_0x_0 + w_1x_1 + w_2x_2 + \cdots + w_mx_m$$
$$(w_0 ,切片 : x_0=1)$$
ベクトルで表すと以下の通りになります。
\hat{y} = (\begin{array} xx_0&x_1&\cdots&x_m \end{array})
\begin{pmatrix}
w_0 \\
w_1 \\
\vdots \\
w_m \\
\end{pmatrix}
$$\hat{y} = \boldsymbol{x}^T \boldsymbol{w}$$
$x$ベクトルは一つではありません。多数の教師データから、回帰係数を導出します。よって、$x$横ベクトルをサンプルサイズ分だけ縦方向に並べた行列を$X$とします。また、教師データの数だけ予測値も出てくるので、その値を並べたベクトルを$y$ベクトルと定義します。式で表した方が分かりやすいと思います。サンプルサイズを$n$として式に表してみます。
\begin{pmatrix}
y_1 \\
y_2 \\
y_3 \\
y_4 \\
y_5 \\
\vdots \\
y_n
\end{pmatrix} = \begin{pmatrix}
1 & x_{11} & \cdots & x_{m1} \\
1 & x_{12} & \cdots & x_{m2} \\
1 & x_{13} & \cdots & x_{m3} \\
1 & x_{14} & \cdots & x_{m4} \\
1 & x_{15} & \cdots & x_{m5} \\
\vdots & \vdots & \ddots & \vdots \\
1 & \cdots & \cdots & x_{mn}
\end{pmatrix}
\begin{pmatrix}
w_0 \\
w_1 \\
\vdots \\
w_m
\end{pmatrix}
$$\boldsymbol{\hat{y}} = X\boldsymbol{w}$$
最小二乗法
予測値$\hat{y}$と実際の$y$に隔離が無いように、重み$w$を求めて行きますが、重回帰分析では最小二乗法を使います。以下の通りに表される損失関数$L$を最小化させる様にパラメータを決定します。
$$L=\sum_{i=1}^{n}(y_i - \hat{y_i})^2$$
$y_i - \hat{y_i}$ については、 $\hat{y}$ベクトルと $y$ベクトルの成分同士の引き算と見ることができると思います。また、上式はベクトルの内積、若しくはL2ノルムの二乗で表すことが出来ます。
(\begin{array} yy_1 - \hat{y_1}&y_2 - \hat{y_2} &\cdots&y_n - \hat{y_n} \end{array})
\begin{pmatrix}
y_1 - \hat{y_1} \\
y_2 - \hat{y_2} \\
\vdots \\
y_n - \hat{y_n}
\end{pmatrix}
$$ (\boldsymbol{y} - \boldsymbol{\hat{y}})^T(\boldsymbol{y} - \boldsymbol{\hat{y}})$$
$$ ||\boldsymbol{y} - \boldsymbol{\hat{y}}||^2 $$
上記の式と先ほどの⑴式から以下の通りに損失関数を導くことができます
$$ L = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})$$
$$ L = (\boldsymbol{y}^T - \boldsymbol{w}^T X^T)(\boldsymbol{y} - X\boldsymbol{w})$$
$$ L = \boldsymbol{w} ^T X^T X \boldsymbol{w} - \boldsymbol{w} ^T X^T \boldsymbol{y} - \boldsymbol{y}^T X \boldsymbol{w} + \boldsymbol{y}^T \boldsymbol{y} $$
ここで第2項と第3項は同値であり、以下の通りに式変形することが可能です。(理由;2項と3項は転置の関係にあり、更に両方ともスカラーであることから、同値である事が分かる)
$$ L = \boldsymbol{w} ^T X^T X \boldsymbol{w} - 2\boldsymbol{y}^T X \boldsymbol{w} + \boldsymbol{y}^T \boldsymbol{y} $$
この式を$\boldsymbol{w}$の各成分で偏微分し、一次導関数が0ベクトルとなる$w$を求めます。
$$ \frac{\partial L}{\partial \boldsymbol{w}} = 2X^T X \boldsymbol{w} - 2X^T \boldsymbol{y} + O \cdots (1)$$
$\frac{\partial L}{\partial \boldsymbol{w}} = O$とすると
$$ 2X^T X \boldsymbol{w} = 2X^T \boldsymbol{y}$$
今、$X^T X$は正方行列であり逆行列が存在するため
$$ \boldsymbol{w} = (X^T X)^{-1} X^T \boldsymbol{y} $$
これで求めるべき$\boldsymbol{w}$が分かりました。尚、$X^T X$に逆行列が存在しない場合、上式の解は定まりません。これが言わゆる多重共線性問題に繋がってきます。
リッジ回帰
正則化項
重回帰分析の損失関数に正則化項を加えたものがリッジ回帰、及びラッソ回帰になります。
$$ L = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \alpha|| \boldsymbol{w} ||_{2}^2\cdots (2)$$
(2)式はリッジ回帰の式になるのですが、右に出てきているのが正則化項となります。尚、リッジ回帰ではL2ノルムの二乗、ラッソ回帰ではL1ノルムを正則化項として使います。リッジ回帰では正則化項を加えることで、パラメータ$\boldsymbol{w}$の各成分を全体的に滑らかにする事ができます。(ノルムをなるべく小さくしようとするので)
因みに、$\alpha$はハイパーパラメータとなり、自由に決めてよい値になります。値が大きほど正則化項の影響が大きくなりますので、モデルの精度を見ながら変えていきます。
〜L2ノルムとL1ノルム〜
- L2ノルム...いわゆるユークリッド距離と呼ばれるもので、ベクトル成分同士の差の二乗和の平方根になります。
- L1ノルム...マンハッタン距離と呼ばれます。ベクトル成分同士の差の絶対値の和になります。
上記(2)式の正則化項は$\alpha\boldsymbol{w}^T\boldsymbol{w}$と表されることが分かります。先ほどの重回帰分析を参考にして微分していくと最終的に以下の通りになります。
$$ \frac{\partial L}{\partial \boldsymbol{w}} = 2X^T X \boldsymbol{w} - 2X^T \boldsymbol{y} + O + 2\alpha\boldsymbol{w}$$
これが0ベクトルとなるようなパラメータ$\boldsymbol{w}$は結局
$$ \boldsymbol{w} = (X^T X + \alpha I)^{-1} X^T \boldsymbol{y} $$
となります。(Iは単位行列)
リッジ回帰の実装
前回の重回帰分析でも実装をしてみましたが、今回の同じようにリッジ回帰を実装してみます。使うデータセットはscikit-learnのボストンハウジング、環境はJupyterNotebookです。まずは普通にscikit-learnで
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.datasets import load_boston
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
%matplotlib inline
sns.set()
boston = load_boston()
X, y = boston.data, boston.target
X = StandardScaler().fit_transform(X)
clf1 = LinearRegression().fit(X, y)
clf2 = Ridge(alpha=10).fit(X, y)
clf3 = Ridge(alpha=100).fit(X, y)
plt.plot(clf1.coef_, label='alpha=0', color='r', linestyle=':')
plt.plot(clf2.coef_, label='alpha=10', color='g', linestyle='-.')
plt.plot(clf3.coef_, label='alpha=100', color='b', linestyle='--')
plt.xlabel('Features', fontsize=12)
plt.ylabel('Coefficient', fontsize=12)
plt.legend();

次に、scikit-learnを使わずに書いてみます。
class Ridge2:
def __init__(self, alpha=1):
self.w_ = None
self.alpha = alpha
def fit(self, X, y):
X = np.insert(X, 0, 1, axis=1)
I = np.eye(X.shape[1])
self.w_ = np.linalg.inv(X.T @ X + self.alpha*I) @ X.T @ y
def predict(self, X):
X = np.insert(X, 0, 1, axis=1)
return X @ self.w_
clf4 = Ridge2(alpha=10)
clf4.fit(X, y)
coef_df = pd.DataFrame({'clf2': clf2.coef_,
'clf4': clf4.w_[1:]},
index=boston.feature_names)
coef_df

scikit-learnの結果と一致している事が分かります。
ラッソ回帰
数値最適化
ラッソ回帰ではその損失関数を以下の通りに定義します。
$$ L = \frac{1}{2}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \alpha|| \boldsymbol{w} ||_{1}\cdots (3) $$
L1ノルムはその定義からも分かる通り、絶対値が出てきており、L2ノルムのように一気にベクトルで微分してその最適解を求めるという処理が出来ません。左微分と右微分を駆使して最適化を行っていくのですが、重回帰やリッジよりも少し難しいです。
ラッソ回帰の最適化アルゴリズムはいくつか種類があるらしいのですが、自分はCD(Coordinate Descent;座標降下法)と言う手法しか勉強していないので、こちらの手法で手順を追っていきたいと思います。
座標降下法は名前の割に単純なアイデアです。まず$\boldsymbol{w}$の初期値を決めます。そこからまず$ \frac{\partial L}{\partial w_1} = 0 $となる様な$w_1$を求めます。次に$\frac{\partial L}{\partial w_2} = 0$となる$w_2$を求めます。この操作を全ての$w_d$で行い少しずつ$L$の最小化を目指していく形になります。全ての変数を同時に動かして$\frac{\partial L}{\partial \boldsymbol{w}} = 0$となる様な変数を求める事が難しいので、一つずつ攻めて行って、近似解を求めようと行った手法です。
損失関数の式変形
損失関数を微分していくのですが、ここで気をつけるべきこととして、$w_0$の切片項だけ正則化項が働かないと言う条件が挙げられます。つまり上の(3)式は$w_1$ 〜 $w_d$までにしか適用されず、$w_0$に関しては、正則化項を無視して良い形になります。なので$w_0$から式変形をしていきたいと思います。
他サイトでは式変形を省略して導出していますが、なるべく丁寧にやっていこうとして行ったら、すごく長くなりました。。。
取り敢えず重回帰分析で導出した(1)から始めて行きたいと思います。
$$ \frac{\partial L}{\partial \boldsymbol{w}} = 2X^T X \boldsymbol{w} - 2X^T \boldsymbol{y} + O \cdots (1)$$
ラッソでは損失関数に1/2が掛けられているためこの式は以下の通りに変形されます。
$$ \frac{\partial L}{\partial \boldsymbol{w}} = X^T X \boldsymbol{w} - X^T \boldsymbol{y}$$
=
\begin{pmatrix}
1 & x_{11} & \cdots & x_{1j} \\
1 & x_{21} & \cdots & x_{2j} \\
1 & x_{31} & \cdots & x_{3j} \\
\vdots & \vdots & \ddots & \vdots \\
1 & x_{i1} & \cdots & x_{ij}
\end{pmatrix}^T
\left[
\begin{pmatrix}
1 & x_{11} & \cdots & x_{1j} \\
1 & x_{21} & \cdots & x_{2j} \\
1 & x_{31} & \cdots & x_{3j} \\
\vdots & \vdots & \ddots & \vdots \\
1 & x_{i1} & \cdots & x_{ij}
\end{pmatrix}
\begin{pmatrix}
w_0 \\
w_1 \\
\vdots \\
w_j
\end{pmatrix}
-
\begin{pmatrix}
y_1 \\
y_2 \\
y_3 \\
\vdots \\
y_i
\end{pmatrix}
\right]
=
\begin{pmatrix}
1 & 1 & \cdots & 1 \\
\cdots & \cdots & \cdots & \cdots \\
\cdots & \cdots & \cdots & \cdots \\
\vdots & \vdots & \ddots & \vdots \\
\cdots & \cdots & \cdots & \cdots
\end{pmatrix}
\left[
\begin{pmatrix}
1 & x_{11} & \cdots & x_{1j} \\
1 & x_{21} & \cdots & x_{2j} \\
1 & x_{31} & \cdots & x_{3j} \\
\vdots & \vdots & \ddots & \vdots \\
1 & x_{i1} & \cdots & x_{ij}
\end{pmatrix}
\begin{pmatrix}
w_0 \\
w_1 \\
\vdots \\
w_j
\end{pmatrix}
-
\begin{pmatrix}
y_1 \\
y_2 \\
y_3 \\
\vdots \\
y_i
\end{pmatrix}
\right]
=
\begin{pmatrix}
1 & 1 & \cdots & 1 \\
\cdots & \cdots & \cdots & \cdots \\
\cdots & \cdots & \cdots & \cdots \\
\vdots & \vdots & \ddots & \vdots \\
\cdots & \cdots & \cdots & \cdots
\end{pmatrix}
\left[
\begin{pmatrix}
w_0 + w_1x_{11} + \cdots \\
\cdots \\
\cdots \\
\cdots \\
\cdots
\end{pmatrix}
-
\begin{pmatrix}
y_1 \\
y_2 \\
y_3 \\
\vdots \\
y_i
\end{pmatrix}
\right]
いい感じで、左項の1行目が全て1になってくれます。よって$w_0$で微分した結果($ = \frac{\partial L}{\partial \boldsymbol{w}}$ベクトルの第一成分)に関しては、右のベクトルで出てきた成分の単純な和になる事が分かります。よって以下の通りになる事が分かります。
$$
\frac{\partial L}{\partial w_0} = \sum^n_{i=1}\left(w_0 + \sum^d_{j=1}x_{ij}w_{j} - y_i \right) \cdots (4)
$$
$w_0$だけシグマの外に出ているのは、変数$x$に寄らず、どの行でも常に$w_0$が出てくるからです。(全てに1がかけられているため)
尚、$n$は全データの数(つまり$i$の最後の数)、$d$はデータの次元数(つまり$j$の最後の数)になります。
(↑本当はこのルールに沿って考えた場合、上の長い行列にも$n$と$d$を書かなくてはいけませんが、見えにくいので、敢えて文字を減らしています。)
この式を$=0$として、$w_0$以外の文字を移行すると以下の様になります。
$$
w_0 = \frac{1}{n} \sum^n_{i=1} \left(y_i - \sum^d_{j=1}x_{ij}w_{j} \right)
$$
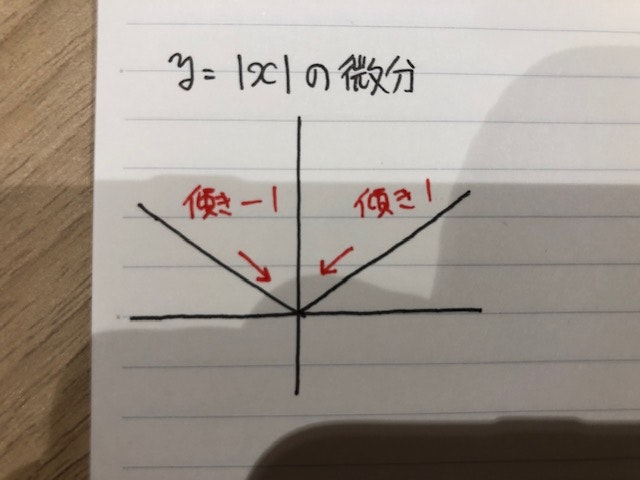
次に$w_0$以外で微分していきますが、こちらは正則化項が出てくるので、右側微分と左側微分を考えていかなければなりません。正則化項の微分に関しては以下の写真を参考にしてください。
正の方向と負の方向、どちらから極限を取るかによって、結果が違ってくる事、更に0でその微分が定義できないことに気をつけます。以上の点と、(4)を参考に$w_k$について、右微分と左微分を求めると(表記が誤っている可能性あります。)
$$
\frac{\partial^+ L}{\partial w_k} = \sum^n_{i=1} \left(w_0 + \sum^d_{j=1}x_{ij}w_{j} - y_i \right)x_{ik} + \alpha \cdots (5.1)
$$
$$
\frac{\partial^- L}{\partial w_k} = \sum^n_{i=1} \left(w_0 + \sum^d_{j=1}x_{ij}w_{j} - y_i \right)x_{ik} - \alpha \cdots (5.2)
$$
先程の$w_0$と違い、積を取るべき$X^T$の行が全て1ではないので、$x_{ik}$の変数が式に出てきています。
更にこの式を$=0$として、$w_k$以外の文字を移行すると以下の様になります。
$$
w_k^+ = \frac{\displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} - \alpha}
{\displaystyle\sum^n_{i=1}x_{ik}^2}
\cdots (6.1)
$$
$$
w_k^- = \frac{\displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} + \alpha}
{\displaystyle\sum^n_{i=1}x_{ik}^2}
\cdots (6.2)
$$
$(j≠k)$の記号ですが、$w_k$は左項に移行しているので、それ以外の$w$を足していくと言う意味です。ブログとは関係ないですが、Latexの練習になりました。。。
ここで、再確認ですが(6.1)は$w_k$が正の値の場合における、$w_k$の更新後の値になります。ところが、下記の条件に当てはまる場合、$w_k$は正にならない事がわかると思います。
$$ \displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} < \alpha $$
つまり通常の重回帰分析で$w_k$の値が正になる様な場合でも、上式の条件に入ってしまった場合、$w_k$は更新できなくなってしまいます。その場合、$w_k$は初期値0のまま更新されません。負の場合も同様です。まとめると以下の様な形になります。
【条件1】
$ \displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} > \alpha $
の場合、
$w_k^+ = \frac{\displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} - \alpha}
{\displaystyle\sum^n_{i=1}x_{ik}^2}
\cdots(6.1)$
【条件2】
$ -\alpha < \displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} < \alpha $
の場合、
$w_k = 0$
【条件3】
$ \displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} < -\alpha $
の場合、
$
w_k^- = \frac{\displaystyle\sum^n_{i=1} \left(y_i - w_0- \sum^d_{j=1(j≠k)}x_{ij}w_{j} \right)x_{ik} + \alpha}
{\displaystyle\sum^n_{i=1}x_{ik}^2}
\cdots (6.2)
$
以上が$w_k$の更新後の値となります。以上の事からも分かりますが、L1ノルムを正則化項として加えた場合、パラメータ$\boldsymbol{w}$の多くが0になってしまう事が分かると思います。これがいわゆる**『スパースな解』**になります。
scikit-learnでの実装
先程のボストンハウジングでラッソ回帰の挙動を確認してみようと思います。
clf5 = Lasso(alpha=1).fit(X, y)
plt.plot(clf1.coef_, label='LinearRegression', color='r', linestyle=':')
plt.plot(clf5.coef_, label='Lasso alpha=1', color='g', linestyle='-.')
plt.plot(clf3.coef_, label='Ridge alpha=100', color='b', linestyle='--')
plt.xlabel('Features', fontsize=10)
plt.ylabel('Coefficient', fontsize=10)
plt.legend();

通常の重回帰分析やリッジ回帰と比較すると各特徴量における回帰係数が0になっている事が確認できます。よりシンプルで分かりやすいモデルとも言えます。
終わりに
- 今回、ブログを通してイマイチ理解できてなかった部分を少しだけクリアにできた。(まだ分かってない部分も多いですが・・・)
- L1、L2ノルムによる正則化はリッジやラッソに関わらず頻出なので、勉強してよかった。