1. 目的
筆者自身の勉強が主目的。なんでもいいから強化学習を実践してみたかった。
本記事では、下図のような「じゃんけん鬼ごっこ」を強化学習で実現する。
グーはパーから逃げ、チョキを追い、
パーはチョキから逃げ、グーを追う。
2. 理論と計画
2-1. 強化学習とは?12345
ゲームの最強の攻略方法を機械的に見つける方法。
強化学習では、 PDCAサイクルではなく、DCAサイクルを回す 。
- Do: まずは適当に「行動」する
- Check: 適当に動いた結果、「報酬(スコア)」を得る。
- Act: 得た報酬と、今の 「状態」 をもとに、行動戦略を練り直す。
- 再びDo: 練り直した行動戦略に従って動く。
- ...
上記からも分かる通り、強化学習には 「行動」、 「報酬」 、 「状態」 が欠かせない。
何度も泥臭い 「行動」 を繰り返し、その度に 「報酬」 を受け取り、どうすれば(どんな 「状態」 のときにどんな 行動 を取れば)よりたくさんスコアがもらえるかを「探って」いくのが強化学習である。
この「探り方」にはいろいろあるが、そのうち代表的な3つが「Q学習」、「Sarsa法」、そして「モンテカルロ法」である。
今回はQ学習を実装するが、Sarsa法、モンテカルロ法についても簡単に解説する。
2-1-1. Q学習とは?
Q学習のQとは、「価値」である。どれだけ報酬がもらえそうかの予想値を価値と呼んでいる。
状態と行動から、もらえそうな報酬の予想値を求められる関数 $Q_{時刻}(状態, 行動)$ を考える。
この $Q_{時刻}$ の精度を時刻(ステップ)6が経過するにつれて高めていこうという学習の一つが、Q学習である。
ノリとしては、
$$(今の状態と行動の価値)_{最新情報} = (1-\alpha)(今の状態と行動の価値)_{古い情報}
+ \alpha・(報酬に基づく成分)$$
としたい・・・①。 $\alpha$ は学習率といい、どれだけ激しく $Q$ を更新するかを表している。
$0$以上の整数により、ステップ $t$ を考える。
ステップ $t$ のときの状態を $s_t$, 行動を $a_t$, 報酬を $r_t$ 書くことにすると、
①は
$$Q_{t}(s_{t}, a_{t}) = (1-\alpha)Q_{t-1}(s_t, a_t) + \alpha・(r_tに基づく成分)$$
のようにかける・・・②。
さて、$(r_tに基づく成分)$ は $(r_t + \gamma・(次の状態と行動の価値))$ のようにしたい・・・③。
直感的に言えば、②③は、「今の状態と行動の価値」の情報 を$100(1-\alpha)\%$だけ残し、残りの $100\alpha\%$ を、『「今の報酬」と「次の状態と行動の価値の$\gamma$倍」の和』を用いて更新している。
$\gamma$ は「割引残率」(または「割引率」)といい、「価値」を考えるときにどれだけ先の未来までを視野に入れるかを表す数値である。
$$Q_{t}(s_{t}, a_{t}) = (1-\alpha)Q_{t-1}(s_{t}, a_{t}) + \alpha・(r_t+\gamma・(ステップt+1での状態と行動の価値))$$
・・・④
割引残率について、詳しく
「割引残率」を『「価値」を考えるときにどれだけ先の未来までを視野に入れるかを表す数値』と説明したが、より正確には、『「価値」の計算に未来の報酬予想値をどれだけ強く含めるか』という指標である。
$$Q_{t}(s_{t}, a_{t}) = (1-\alpha)Q_{t-1}(s_{t}, a_{t}) + \alpha・(r_t+\gamma・(ステップt+1での状態と行動の価値))$$
と書くことが出来、さらに
$(ステップt+1での状態と行動の価値) = (1-\alpha)... + \alpha・(r_{t+1}+\gamma・(ステップt+2での状態と行動の価値))$
$(ステップt+2での状態と行動の価値) = (1-\alpha)... + \alpha・(r_{t+2}+\gamma・(ステップt+3での状態と行動の価値))$
$(ステップt+3での状態と行動の価値) = ...$
と再帰的に続けることが出来ることを考えると、
ステップ$t$での状態と行動の価値 ($Q_{t}(s_{t}, a_{t})$) にはステップ$t+n$ での状態と行動の価値が$(\alpha\gamma)^n$倍だけ含まれていることが分かる。
$\gamma$ が小さければ、未来の状態と行動の価値(未来の$Q$値)が強く割り引かれ、反映されにくくなるというわけだ。
多くの資料では、 $\gamma$ を「割引率」と呼んでいるが、
この呼称だと、 $\gamma$ が大きいほど、未来の$Q$値が強く割り引かれるような誤解を招く。
実際には、$\gamma$ が大きいほど、未来の$Q$値が割り引かれずに「残る」 ようになる、のにもかかわらずだ。
そこでこの記事では独自に、 $\gamma$ を 割引残率と呼んでいる。
「割引 残 率」という呼び名であれば、 $\gamma$ が大きいほど、未来の$Q$値が 残る という実態をより自然に表せるだろう。
(割引残率について、詳しく 終わり)
さて、④で、$(ステップt+1での状態と行動の価値)$ をどんな式にしようか。
一番率直なのは
$$(ステップt+1での状態と行動の価値) = Q_{t-1}(s_{t+1}, a_{t+1})$$
とすることだろう。これは Sarsa法 とよばれる手法である。
一方、Q学習では、
$$(ステップt+1での状態と行動の価値) = \max_{a_{t+1}'}Q_{t-1}(s_{t+1}, a_{t+1}')$$
とする。
わざわざ $a_{t+1}$ と異なる $a_{t+1}'$を使って Q を更新するのは不自然かもしれないが、
ステップ $t$ からみて、 $t+1$ は未来であるため、 どの行動が $a_{t+1}$ であるかは、実際に行動するまでわからない。そのため、「$t+1$時点では、最も高い価値の見込める行動をとるだろう」と仮定して$t$時点の状態、行動の価値を更新するのは、不自然なことではないといえるかもしれない。
逆にSarsa では、$a_{t+1}$ を確定させるため、ステップ$t$の時点で未来$t+1$の行動をあらかじめ決めておく必要があり、その意味では Sarsaこそ不自然という考え方もあるかもしれない。
結局、Q学習の式は
$$Q_{t}(s_{t}, a_{t}) = (1-\alpha)Q_{t-1}(s_{t}, a_{t}) + \alpha・(r_{t} + \gamma \max_{a_{t+1}'}Q_{t-1}(s_{t+1}, a_{t+1}'))$$
となる。 (但し、 引数が $(s_{t}, a_{t})$以外のとき、 $Q_{t} = Q_{t-1}$)
2-1-2. Sarsa法とは?
Sarsa法の概要は、2-1-1節「Q学習とは?」で同時に説明した通りである。
Sarsa法の式は
$$Q_{t}(s_{t}, a_{t}) = (1-\alpha)Q_{t-1}(s_{t}, a_{t}) + \alpha・(r_{t} + \gamma Q_{t-1}(s_{t+1}, a_{t+1}))$$
となる。 (但し、 引数が $(s_{t}, a_{t})$以外のとき、 $Q_{t} = Q_{t-1}$)
2-1-3. モンテカルロ法とは?
さて、Q学習とSarsa法では、どちらも「各ステップ$t$に報酬$r_t$が貰える」という前提で$Q_t$を更新していた。
しかし、問題によっては「各ステップに報酬が貰えるわけではない」という場合もある。
例えば、囲碁やオセロといったゲーム7がそれだ。一手一手を好手、悪手として評価することは、プロ棋士にしかできないだろう。
そこで、「勝ったら$+1$、負けたら$-1$、引き分けなら$0$の報酬を与える」、「反則したら反則する度に$-0.1$の報酬を与える」のように、勝負が終わったときや、特定の条件が揃ったときのみに報酬を与えることが考えられる。
このような場合に使えるのがモンテカルロ法だ。
モンテカルロ法は「逐一訪問モンテカルロ法」と「初回訪問モンテカルロ法」の2つに分けられる。
逐一訪問モンテカルロ法では、次のことする。
- 関数 $N(状態, 行動)$、 $G(状態, 行動)$、 $Q(状態, 行動)$ を、任意の引数に対して$0$を返すようにする。
- ゲーム(エピソード)6番号$e$ ($1~e_\max$) について...
- エピソードを実行する
- 各ステップ $t$ ($1~$)について...
- $G(s_{e,t}, a_{e,t})$ を $r_{e,t} + \gamma r_{e,t+1} + \gamma^2 r_{e,t+2} + ...$ だけ増やす8
- $N(s_{e,t}, a_{e,t})$ を $1$ だけ増やす
- $Q(s_{e,t},a_{e,t})$ を $\frac
{G(s_{e,t}, a_{e,t}) - Q(s_{e,t},a_{e,t})
}{N(s_{e,t},a_{e,t})}$ だけ増やす
(より正確な表現... )
上記の説明では、エピソード$e$, ステップ$t$ の$N$ を $N_{e,t}$ のように分けて書いていないため、曖昧さがある。エピソードとステップごとに関数を区別し、関数の「上書き」を回避すると、次のようになる。
- 関数 $N_{-1,-1}(状態, 行動)$、 $G_{-1,-1}(状態, 行動)$、 $Q_{-1,-1}(状態, 行動)$ を、任意の引数に対して$0$を返すようにする。
- ゲーム(エピソード)番号$e$ ($0~e_\max$) について...
- エピソードを実行する (ステップ $t$を $0$ から $t_{\max,e}$ まで進める)
- 各ステップ $t$ ($0~t_{\max,e}$) について...
- $G_{e,t}(s_{e,t}, a_{e,t}) = G_{e,t-1}(s_{e,t}, a_{e,t}) + r_{e,t} + \gamma r_{e,t+1} + \gamma^2 r_{e,t+2} + ...$ とする
- それ以外の引数については $G_{e,t} = G_{e,t-1}$ とする。
- $G_{e,-1}$ は $G_{e-1, t_{\max,e-1}}$、 $t_{\max,-1}$ は $-1$ と読み替えること
- $N_{e,t}(s_{e,t}, a_{e,t}) = N_{e,t-1}(s_{e,t}, a_{e,t}) + 1$ とする
- それ以外の引数については $N_{e,t} = N_{e,t-1}$ とする。
- $N_{e,-1}$ は $N_{e-1, t_{\max,e-1}}$、 $t_{\max,-1}$ は $-1$ と読み替えること
- $Q_{e,t}(s_{e,t},a_{e,t}) = Q_{e,t-1}(s_{e,t},a_{e,t}) + \frac
{G_{e,t}(s_{e,t}, a_{e,t}) - Q_{e,t-1}(s_{e,t},a_{e,t})
}{N_{e,t}(s_{e,t},a_{e,t})}$ とする- それ以外の引数については $Q_{e,t} = Q_{e,t-1}$ とする。
- $Q_{e,-1}$ は $Q_{e-1, t_{\max,e-1}}$、 $t_{\max,-1}$ は $-1$ と読み替えること
- $G_{e,t}(s_{e,t}, a_{e,t}) = G_{e,t-1}(s_{e,t}, a_{e,t}) + r_{e,t} + \gamma r_{e,t+1} + \gamma^2 r_{e,t+2} + ...$ とする
(より正確な表現 終わり)
$N$ は、状態と行動の組み合わせの出現回数をカウントしており、 $G$ は未来に貰えそうな報酬の予想値を計算している。 $G$ を $N$で割ることで、「毎回異なる値に更新されて答えに向かわなくなる」ということを防ぎつつ、価値 $Q$ を更新している。
一方、初回訪問モンテカルロ法は、各エピソード、各ステップごとに$Q$を更新するのではなく、各エピソードの各(状態, 行動) ごとに1回だけ$Q$を更新する。同じ(状態, 行動) が続いていれば、その分だけ更新作業をサボるのが初回訪問モンテカルロ法である。
この記事では、今後単に「モンテカルロ法」といったときは、逐一訪問モンテカルロ法を指すものとする。
余談: モンテカルロ法の式が④式の形になっていることの確認
モンテカルロ法の$Q$更新式は
$$Q_{e,t}(s_{e,t},a_{e,t}) = Q_{e,t-1}(s_{e,t},a_{e,t}) + \frac
{G_{e,t}(s_{e,t}, a_{e,t}) - Q_{e,t-1}(s_{e,t},a_{e,t})
}{N_{e,t}(s_{e,t},a_{e,t})}$$
つまり
$$Q_{e,t}(s_{e,t},a_{e,t}) = \left(1-\frac{1}{N_{e,t}(s_{e,t},a_{e,t})}\right)Q_{e,t-1}(s_{e,t},a_{e,t}) + \frac
{1
}{N_{e,t}(s_{e,t},a_{e,t})}G_{e,t}(s_{e,t}, a_{e,t})$$
であるが、$N_{e,t}(s_{e,t},a_{e,t})$ を $\frac{1}{\alpha_{e,t}}$ としてしまえば
$$Q_{e,t}(s_{e,t},a_{e,t}) = \left(1-\alpha_{e,t}\right)Q_{e,t-1}(s_{e,t},a_{e,t}) + \alpha_{e,t} G_{e,t}(s_{e,t}, a_{e,t})$$
となる。さらに $G_{e,t}(s_{e,t}, a_{e,t}) = r_{e,t} + \gamma (r_{e,t+1} + \gamma r_{e,t+2} + ...)$ であるから、これを代入すると、
$$Q_{e,t}(s_{e,t},a_{e,t}) = \left(1-\alpha_{e,t}\right)Q_{e,t-1}(s_{e,t},a_{e,t}) + \alpha_{e,t} \cdot (r_{e,t} + \gamma (r_{e,t+1} + \gamma r_{e,t+2} + ...))$$
となり、Q学習やSarsa法同様、④式
$$Q_{t}(s_{t}, a_{t}) = (1-\alpha)Q_{t-1}(s_{t}, a_{t}) + \alpha・(r_t+\gamma・(ステップt+1での状態と行動の価値))$$
と同じ形になる。
(余談 終わり)
2-1-4. 行動はどう決めるの?
強化学習において、ステップ$t$ における行動 $a_t$ の決め方は様々考えられる。
基本的には$Q_{t-1}(s_t, a')$ を最大にするような $a'$ を $a_t$ として採用したいが、
常にそうしてしまうと、まだ十分に探索されていない選択肢がとられなくなってしまうため、より最適な行動を学習する機械を逃してしまう恐れがある。
そこで、 確率 $\varepsilon$ でランダムな行動を選び、確率 $1-\varepsilon$ で$Q_{t-1}(s_t, a')$ を最大にするような $a'$ を選ぶという方法が考えられる。
この $\varepsilon$ を探索率という。
このような行動の決め方を「ε-greedy法」という。
2-2. じゃんけん鬼ごっこ
環境に エージェント 「グー」、「チョキ」、「パー」の3体を置き、2次元トーラス平面を自由に動き回れるものとする。
各エージェントには、表2-2-1のとおり、「天敵」と「獲物」が1体ずついる。
直感的に言えば、「じゃんけんの関係」になっている。
表2-2-1. エージェントの敵対関係
| 自分 | 天敵 | 獲物 |
|---|---|---|
| グー | パー | チョキ |
| チョキ | グー | パー |
| パー | チョキ | グー |
各エージェントは、天敵に触れると罰として負の報酬を受け取り、獲物に触れると正の報酬を受け取る。
以上のようなシミュレーションを本記事では「じゃんけん鬼ごっこ」と呼ぶことにする。
2-2-1. 状態数と行動パターン数の制約
状態数と行動パターン数の積は$Q$関数の全パターン数である。本記事では、これを$1048575$ 以下であるようにする。これは、Excelが最大 $1048576$行しか処理できず、そのうち$1$行はヘッダに使われるからだ。
$Q$関数の全パターン数が$1048575$ 以下であると、学習中の$Q$関数の中身をExcelで確認出来て、何かと便利だ。
2-2-2. 状態
状態は、「天敵の距離」、「天敵の向き」、「獲物の距離」、「獲物の向き」、「自分の速さ」の5項目とする。
各項目は、それぞれ
距離リスト、向きリスト、速さリスト から、最も近いものを選ぶものとする。
状態数は len(距離リスト) * len(向きリスト) * len(距離リスト) * len(向きリスト) * len(速さリスト) となる。
2-2-3. 行動
行動は、「速さの変化」、「向きの変化」の2項目とする。
各項目は、それぞれ
速さの変化リスト、 向きの変化リスト から、最も近いものを選ぶものとする。
行動パターン数は len(速さの変化リスト) * len(向きの変化リスト) となる。
2-2-4. 報酬
報酬は、「速さに基づく報酬」と「天敵と獲物に基づく報酬」の和として、各ステップ各エージェントに与えられるものとする。
速さに基づく報酬は、 $-(速さ報酬係数)|(実際の速さ) - (目標速さ)|$ とし、速さ報酬係数($0$以上)と目標速さはハイパーパラメータとする。
天敵と獲物に基づく報酬は、
- 天敵に触れたとき、 $-(捕食報酬)$
- 天敵に触れずに獲物に触れたとき、 $+(捕食報酬)$
- その他のとき、 $0$
とする。
ただし、「天敵または獲物に触れる」とは、距離$10$以内に接近することを意味するものとし、
捕食報酬はハイパーパラメータとする。
2-2-5. 「方向」と「向き」の違い
- 「方向」も「向き」も $0$ 以上 $2\pi$ 未満である
- 「方向」 は、各エージェントの正面と$x$軸が為す角度である。
但し、正面が$y$軸である場合、方向は $\pi/4$ であるとする。 - 「向き」は、自分からみた相手の相対的な角度である。
- 例えば、グーから見たチョキの「向き」は
${\rm arctan2}((チョキの座標) - (グーの座標)) - (グーの方向)$
である。 - 但し、相手との座標の差分を求める際には、環境がトーラス構造になっていることに注意し、
最短距離になる相手座標を選ぶ必要がある。
- 例えば、グーから見たチョキの「向き」は
3. 実験
3-1. ファイル構成
./ ※4
├ hand_imgs/ ※1
│ ├ gu.png
│ ├ choki.png
│ └ pa.png
├ imgs/ ※3
└ base.py ※2
※1 いらすとや https://www.irasutoya.com/2013/07/blog-post_5608.html からダウンロードし、グーの画像は gu.png, チョキの画像は choki.png, パーの画像は pa.png と名前を変更して保存
※2 base.py は、「基本コード」であり、実験用コードのひな型である。 3-2節で中身を説明する。
※3 base.pyを元にした実験用コードを実行すると、 imgs/ 内にエージェントの位置関係がステップごとに画像として保存される
※4 base.pyを元にした実験用コードを実行すると、 カレントディレクトリには 各エージェントのQテーブルを表す csv ファイルが $100000$ ステップごとに保存される
3-2. 基本コード ./base.py
次のとおり。
(クリックして ./base.py を表示する)
import numpy as np
import pandas as pd
import itertools
import matplotlib
matplotlib.use("Agg") # Tkinter エラーを回避
import matplotlib.pyplot as plt
from matplotlib.offsetbox import OffsetImage, AnnotationBbox
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 10
目標速さ = 1
環境の幅 = 250
環境の高さ = 250
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), (2 * np.pi / 10)]
速さの変化リスト = [-1, 1]
# 状態数と行動パターン数の確認
状態数 = (len(距離リスト) * len(向きリスト))**2 * len(速さリスト)
行動パターン数 = len(方向の変化リスト) * len(速さの変化リスト)
print(f"""状態数: {状態数}, 行動パターン数: {行動パターン数}, \
Qテーブルサイズ: {状態数 * 行動パターン数}""")
assert 状態数 * 行動パターン数 <= 1048575, "状態数と行動パターン数が多すぎます"
class 環境型:
def __init__(self):
self.__ステップ = 0
self.エージェントたち = [
エージェント型(self, 手) for 手 in ["グー", "チョキ", "パー"]
]
self.__捕食者 = None
self.__被食者 = None
@property
def ステップ(self): return self.__ステップ
@property
def 幅(self): return 環境の幅
@property
def 高さ(self): return 環境の高さ
def ステップを進める(self):
for エージェント in self.エージェントたち:
エージェント.行動する()
報酬たち = self.エージェントたちの報酬を求める()
for (エージェント, 報酬) in zip(self.エージェントたち, 報酬たち):
エージェント.学習する(報酬)
if (
0 <= self.__ステップ % 100000 and self.__ステップ % 100000 < 300
) or (2000000 <= self.__ステップ):
try:
self.画像を作る("./imgs")
except:
plt.close("all")
if self.__ステップ % 100000 == 0:
try:
df = self.エージェントたち[0].Q.df
df.to_csv(
f"./Q_{self.__ステップ}_グー.csv",
index=False, encoding="cp932"
)
del df
df = self.エージェントたち[1].Q.df
df.to_csv(
f"./Q_{self.__ステップ}_チョキ.csv",
index=False, encoding="cp932"
)
del df
df = self.エージェントたち[2].Q.df
df.to_csv(
f"./Q_{self.__ステップ}_パー.csv",
index=False, encoding="cp932"
)
del df
except Exception:
pass
self.__ステップ += 1
def エージェントたちの報酬を求める(self):
報酬たち = []
self.__捕食者 = None
self.__被食者 = None
for エージェント in self.エージェントたち:
速さに基づく報酬 = - 速さ報酬係数 * abs(
エージェント.速さ - 目標速さ
)
天敵 = [
相手 for 相手 in self.エージェントたち
if 相手.手 == エージェント.天敵
][0]
天敵に触れている = エージェント.距離と向きを調べる(天敵)[0] <= 10
獲物 = [
相手 for 相手 in self.エージェントたち
if 相手.手 == エージェント.獲物
][0]
獲物に触れている = エージェント.距離と向きを調べる(獲物)[0] <= 10
if 天敵に触れている:
天敵と獲物に基づく報酬 = - 捕食報酬
self.__被食者 = エージェント
elif 獲物に触れている:
天敵と獲物に基づく報酬 = 捕食報酬
self.__捕食者 = エージェント
else:
天敵と獲物に基づく報酬 = 0
報酬 = 速さに基づく報酬 + 天敵と獲物に基づく報酬
報酬たち.append(報酬)
return 報酬たち
def 画像を作る(self, folder):
plt.figure(figsize=(6, 6))
colors = {"グー": "red", "チョキ": "green", "パー": "blue"}
paths = {
"グー":"./hand_imgs/gu.png", "チョキ":"./hand_imgs/choki.png",
"パー":"./hand_imgs/pa.png"
}
# グラフに画像と円をプロットする
for エージェント in self.エージェントたち:
(x, y) = エージェント.位置
circle = plt.Circle(
(x, y), 5, color=colors[エージェント.手], fill=True
)
plt.gca().add_patch(circle)
(artists, im) = imscatter(x, y, paths[エージェント.手], zoom=.05)
del im
# 捕食者に応じてグラフを塗りつぶす
if self.__捕食者 is None and self.__被食者 is None:
pass
else:
if self.__捕食者 is None:
# グー、チョキ、パー全員が1箇所に集まった場合
# → 全員が被食者で捕食者はいない
塗りつぶし色 = "k" # 黒
else:
塗りつぶし色 = colors[self.__捕食者.手]
plt.gca().axvspan(0, 環境.幅, color=塗りつぶし色, alpha=0.1)
plt.xlim(0, self.幅)
plt.ylim(0, self.高さ)
plt.xlabel("X")
plt.ylabel("Y")
平均速さ = sum(
[エージェント.速さ for エージェント in self.エージェントたち]
) / len(self.エージェントたち)
plt.title(f"""step {self.__ステップ} speed \
({self.エージェントたち[0].速さ:.1f}, {self.エージェントたち[1].速さ:.1f},\
{self.エージェントたち[2].速さ:.1f}) """)
filename = f"{folder.rstrip("/\\")}/step_{self.__ステップ:010d}.png"
try:
plt.savefig(filename)
except:
pass
plt.close("all")
class エージェント型:
def __init__(self, 環境, 手):
self.__環境 = 環境
self.__手 = 手
self.__x = np.random.rand() * 環境.幅
self.__y = np.random.rand() * 環境.高さ
self.__方向 = np.random.choice(向きリスト, 1)[0]
self.__速さ = np.random.choice(速さリスト, 1)[0]
self.__Q = Qテーブル型()
self.__直前の状態 = None
self.__直前の行動 = None
self.__直前の報酬 = None
@property
def 環境(self): return self.__環境
@property
def 手(self): return self.__手
@property
def 天敵(self):
return {"グー":"パー", "チョキ":"グー", "パー":"チョキ"}[self.手]
@property
def 獲物(self):
return ({"グー", "チョキ", "パー"} - {self.手, self.天敵}).pop()
@property
def Q(self): return self.__Q
@property
def 位置(self): return np.array([self.__x, self.__y])
@位置.setter
def 位置(self, value):
(x, y) = value
self.__x = x % self.__環境.幅
self.__y = y % self.__環境.高さ
@property
def 方向(self): return self.__方向
@方向.setter
def 方向(self, value): self.__方向 = 最も近いものを選ぶ(
value % (2 * np.pi), 向きリスト
)
@property
def 速さ(self): return self.__速さ
@速さ.setter
def 速さ(self, value): self.__速さ = 最も近いものを選ぶ(value, 速さリスト)
def 行動する(self):
現在の行動 = self.行動を選ぶ()
self.方向 += 現在の行動["方向の変化"]
self.速さ += 現在の行動["速さの変化"]
self.位置 += self.速さ * np.array([
np.cos(self.方向), np.sin(self.方向)
])
# 直後のステップのために現在の行動を記録しておく
self.__直前の行動 = 現在の行動
def 学習する(self, 報酬):
"""
Q(直前の状態, 直前の行動)
= (1 - 学習率) * Q(直前の状態, 直前の行動)\
+ 学習率 * (直前の報酬 + 割引残率 * Q(現在の状態, 最良の行動))
"""
現在の状態 = self.状態を調べる()
if self.__直前の状態 is None:
pass
else:
最良の行動 = self.行動を選ぶ(探索率 = 0)
old_Q_直前 = self.__Q[self.__直前の状態, self.__直前の行動]
old_Q_現在 = self.__Q[ 現在の状態, 最良の行動]
new_Q_直前 = (1 - 学習率) * old_Q_直前\
+ 学習率 * (self.__直前の報酬 + 割引残率 * old_Q_現在)
self.__Q[self.__直前の状態, self.__直前の行動] = new_Q_直前
# 直後のステップのために現在の状態と報酬を記録しておく
self.__直前の状態 = 現在の状態
self.__直前の報酬 = 報酬
def 行動を選ぶ(self, 探索率 = 探索率):
if np.random.rand() < 探索率:
行動 = {
"方向の変化": np.random.choice(方向の変化リスト, 1)[0],
"速さの変化": np.random.choice(速さの変化リスト, 1)[0]
}
return 行動
else:
状態 = self.状態を調べる()
暫定最大Q値 = - np.inf
暫定最良行動たち = []
for 方向の変化 in 方向の変化リスト:
for 速さの変化 in 速さの変化リスト:
行動 = {"方向の変化": 方向の変化, "速さの変化": 速さの変化}
Q値 = self.__Q[状態, 行動]
if Q値 > 暫定最大Q値:
暫定最大Q値 = Q値
暫定最良行動たち = [行動]
elif Q値 == 暫定最大Q値:
暫定最良行動たち.append(行動)
最良行動たち = 暫定最良行動たち
最良行動 = np.random.choice(最良行動たち, 1)[0]
return 最良行動
def 状態を調べる(self):
環境 = self.__環境
天敵 = [
エージェント for エージェント in 環境.エージェントたち
if エージェント.手 == self.天敵
][0]
獲物 = [
エージェント for エージェント in 環境.エージェントたち
if エージェント.手 == self.獲物
][0]
(天敵の距離, 天敵の向き) = self.距離と向きを調べる(天敵)
(獲物の距離, 獲物の向き) = self.距離と向きを調べる(獲物)
状態 = {
"天敵の距離": 最も近いものを選ぶ(天敵の距離, 距離リスト),
"天敵の向き": 最も近いものを選ぶ(天敵の向き, 向きリスト),
"獲物の距離": 最も近いものを選ぶ(獲物の距離, 距離リスト),
"獲物の向き": 最も近いものを選ぶ(獲物の向き, 向きリスト),
"速さ": self.速さ
}
return 状態
def 距離と向きを調べる(self, 相手):
環境 = self.__環境
(相手x, 相手y) = 相手.位置
距離と角度の候補たち = []
(Ax, Ay) = self.位置
for i in range(-1, 1+1):
Bx = 相手x + i * 環境.幅
for j in range(-1, 1+1):
By = 相手y + j * 環境.高さ
距離 = float(np.sqrt((By - Ay)**2 + (Bx - Ax)**2))
角度 = np.arctan2(By - Ay, Bx - Ax)
距離と角度の候補たち.append((距離, 角度))
(距離, 角度) = sorted(
距離と角度の候補たち,
key = lambda 距離と角度: 距離と角度[0]
)[0]
向き = (角度 - self.方向) % (2 * np.pi)
return (距離, 向き)
class Qテーブル型:
def __init__(self):
self.__ndarray = np.zeros((
len(距離リスト), len(向きリスト), len(距離リスト), len(向きリスト),
len(速さリスト),
len(方向の変化リスト), len(速さの変化リスト)
))
@property
def df(self): # メモリ不足に注意
全組み合わせ = list(itertools.product(
距離リスト, 向きリスト, 距離リスト, 向きリスト, 速さリスト,
方向の変化リスト, 速さの変化リスト
))
Q値たち = self.__ndarray.flatten()
df_ = pd.DataFrame(全組み合わせ, columns=[
"天敵の距離", "天敵の向き", "獲物の距離", "獲物の向き",
"自分の速さ",
"方向の変化", "速さの変化"
])
df_["Q値"] = Q値たち
return df_
def __getitem__(self, key):
(状態, 行動) = key
return self.__ndarray[
距離リスト.index(状態["天敵の距離"]),
向きリスト.index(状態["天敵の向き"]),
距離リスト.index(状態["獲物の距離"]),
向きリスト.index(状態["獲物の向き"]),
速さリスト.index(状態["速さ"]),
方向の変化リスト.index(行動["方向の変化"]),
速さの変化リスト.index(行動["速さの変化"])
]
def __setitem__(self, key, value):
(状態, 行動) = key
self.__ndarray[
距離リスト.index(状態["天敵の距離"]),
向きリスト.index(状態["天敵の向き"]),
距離リスト.index(状態["獲物の距離"]),
向きリスト.index(状態["獲物の向き"]),
速さリスト.index(状態["速さ"]),
方向の変化リスト.index(行動["方向の変化"]),
速さの変化リスト.index(行動["速さの変化"])
] = value
def 最も近いものを選ぶ(値, 配列):
idx = np.abs(np.array(配列) - 値).argmin()
return 配列[idx]
# https://qiita.com/sabopy/items/b4ed95f713e6d98ab52c を改造
def imscatter(x, y, image, ax=None, zoom=1):
try: len(x)
except: x = [x]
try: len(y)
except: y = [y]
if ax is None:
ax = plt.gca()
try:
image = plt.imread(image)
except:
pass
im = OffsetImage(image, zoom=zoom)
artists = []
for x0, y0 in zip(x, y):
ab = AnnotationBbox(im, (x0, y0), xycoords='data', frameon=False)
artists.append(ax.add_artist(ab))
return (artists, im)
環境 = 環境型()
for _ in range(2002189): # ここは適当にいじる
環境.ステップを進める()
3-2-1. ハイパーパラメータ
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 10
目標速さ = 1
環境の幅 = 250
環境の高さ = 250
学習率, 割引残率, 探索率 は 2-1 節で説明した通り、強化学習に固有のハイパーパラメータである。
捕食報酬, 速さ報酬係数 は、報酬を決定するためのハイパーパラメータである。
目標速さ は、 この速さとエージェントの速さの差の大きさが大きいほど、ペナルティ(負の報酬) を各ステップで受け取るというものであり、ペナルティの大きさは 速さ報酬係数 で決める。
環境の幅 と 環境の高さ は、名前のとおりエージェントが移動する2次元平面の広さを表している。
但しこの2次元平面は端と端が繋がっているトーラス構造をしている。
3-2-2. 状態と行動のリスト
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), (2 * np.pi / 10)]
速さの変化リスト = [-1, 1]
状態と行動の選択肢をリストアップしている。
$Q$テーブルを学習する際は、これらのリストの中から実際の状態に最も近い選択肢を選び、学習に利用する。
最も近い選択肢を選ぶために、コードの下のほうで 最も近いものを選ぶ(値, 配列) 関数 が定義されている。(3-2-6節で解説)
3-2-3. 環境型 クラス
class 環境型:
def __init__(self): #...
# properties...
def ステップを進める(self): #...
def エージェントたちの報酬を求める(self): #...
def 画像を作る(self, folder): #...
環境を表すクラスであり、各エージェントがこのクラスに登録される。
3-2-3-1. コンストラクタとプロパティ
class 環境型:
def __init__(self):
self.__ステップ = 0
self.エージェントたち = [
エージェント型(self, 手) for 手 in ["グー", "チョキ", "パー"]
]
self.__捕食者 = None
self.__被食者 = None
@property
def ステップ(self): return self.__ステップ
@property
def 幅(self): return 環境の幅
@property
def 高さ(self): return 環境の高さ
#...
各エージェント (エージェント型オブジェクト) を登録している。
幅 プロパティ と 高さ プロパティは ハイパーパラメータをそのまま返している。
3-2-3-2. ステップを進める メソッド
class 環境型:
#...
def ステップを進める(self):
for エージェント in self.エージェントたち:
エージェント.行動する()
報酬たち = self.エージェントたちの報酬を求める()
for (エージェント, 報酬) in zip(self.エージェントたち, 報酬たち):
エージェント.学習する(報酬)
if (
0 <= self.__ステップ % 100000 and self.__ステップ % 100000 < 300
) or (2000000 <= self.__ステップ):
try:
self.画像を作る("./imgs")
except:
plt.close("all")
if self.__ステップ % 100000 == 0:
try:
df = self.エージェントたち[0].Q.df
df.to_csv(
f"./Q_{self.__ステップ}_グー.csv",
index=False, encoding="cp932"
)
del df
df = self.エージェントたち[1].Q.df
df.to_csv(
f"./Q_{self.__ステップ}_チョキ.csv",
index=False, encoding="cp932"
)
del df
df = self.エージェントたち[2].Q.df
df.to_csv(
f"./Q_{self.__ステップ}_パー.csv",
index=False, encoding="cp932"
)
del df
except Exception:
pass
self.__ステップ += 1
#...
環境型 には ステップを進める メソッドがあり、
このメソッドでは各エージェントに
- 行動させる (
エージェント.行動する()) - 報酬を与える (
self.エージェントたちの報酬を求める()) - 報酬を元に学習させる (
エージェント.学習する(報酬))
といったことをしており、
また特定のステップにおいて、環境のスナップショットを撮ったり (self.画像を作る(フォルダ))、 各エージェントの $Q$ テーブルを csv 形式で出力したりしている。
3-2-3-3. エージェントたちの報酬を求める メソッド
class 環境型:
#...
def エージェントたちの報酬を求める(self):
報酬たち = []
self.__捕食者 = None
self.__被食者 = None
for エージェント in self.エージェントたち:
速さに基づく報酬 = - 速さ報酬係数 * abs(
エージェント.速さ - 目標速さ
)
天敵 = [
相手 for 相手 in self.エージェントたち
if 相手.手 == エージェント.天敵
][0]
天敵に触れている = エージェント.距離と向きを調べる(天敵)[0] <= 10
獲物 = [
相手 for 相手 in self.エージェントたち
if 相手.手 == エージェント.獲物
][0]
獲物に触れている = エージェント.距離と向きを調べる(獲物)[0] <= 10
if 天敵に触れている:
天敵と獲物に基づく報酬 = - 捕食報酬
self.__被食者 = エージェント
elif 獲物に触れている:
天敵と獲物に基づく報酬 = 捕食報酬
self.__捕食者 = エージェント
else:
天敵と獲物に基づく報酬 = 0
報酬 = 速さに基づく報酬 + 天敵と獲物に基づく報酬
報酬たち.append(報酬)
return 報酬たち
#...
エージェントたちの報酬を求める メソッドでは、
各エージェントの 速さに基づく報酬 と 天敵と獲物に基づく報酬 を計算し、
その和を各エージェントの報酬としている。
報酬の与え方は 2-2-4 節の方針通りである。
また、同時に self.__捕食者 属性 と self.__被食者 属性 を用いて、
誰が誰に捕まったかを特定できるようにしている。
これは、 self.画像を作る(フォルダ) メソッドで環境のスナップショットを撮る際に、誰が誰に捕まったかに応じてグラフを色付けすることに役立つ。
グラフの色付けに基づいて、どのような報酬が発生したかを実験者が容易に把握できるようになる。
3-2-3-4. 画像を作る メソッド
class 環境型:
#...
def 画像を作る(self, folder):
plt.figure(figsize=(6, 6))
colors = {"グー": "red", "チョキ": "green", "パー": "blue"}
paths = {
"グー":"./hand_imgs/gu.png", "チョキ":"./hand_imgs/choki.png",
"パー":"./hand_imgs/pa.png"
}
# グラフに画像と円をプロットする
for エージェント in self.エージェントたち:
(x, y) = エージェント.位置
circle = plt.Circle(
(x, y), 5, color=colors[エージェント.手], fill=True
)
plt.gca().add_patch(circle)
(artists, im) = imscatter(x, y, paths[エージェント.手], zoom=.05)
del im
# 捕食者に応じてグラフを塗りつぶす
if self.__捕食者 is None and self.__被食者 is None:
pass
else:
if self.__捕食者 is None:
# グー、チョキ、パー全員が1箇所に集まった場合
# → 全員が被食者で捕食者はいない
塗りつぶし色 = "k" # 黒
else:
塗りつぶし色 = colors[self.__捕食者.手]
plt.gca().axvspan(0, 環境.幅, color=塗りつぶし色, alpha=0.1)
plt.xlim(0, self.幅)
plt.ylim(0, self.高さ)
plt.xlabel("X")
plt.ylabel("Y")
平均速さ = sum(
[エージェント.速さ for エージェント in self.エージェントたち]
) / len(self.エージェントたち)
plt.title(f"""step {self.__ステップ} speed \
({self.エージェントたち[0].速さ:.1f}, {self.エージェントたち[1].速さ:.1f},\
{self.エージェントたち[2].速さ:.1f}) """)
filename = f"{folder.rstrip("/\\")}/step_{self.__ステップ:010d}.png"
try:
plt.savefig(filename)
except:
pass
plt.close("all")
matplotlib を用いて環境のスナップショットを撮り、引数で指定されたフォルダに保存するメソッド。
またスナップショットは、次の条件に基づいて薄く色付けしている
- グーがチョキを捕まえ、かつパーに捕まっていない時は赤色
- チョキがパーを捕まえ、かつグーに捕まっていない時は緑色
- パーがグーを捕まえ、かつチョキに捕まっていない時は青色
- グーがチョキを捕まえ、チョキがパーを捕まえ、パーがグーを捕まえている時は黒色
- その他 (誰も捕まえていないし捕まってもいない) の時は色付けをしない
また、いらすとやのじゃんけん画像をはめ込むのに用いる imscatter関数は、https://qiita.com/sabopy/items/b4ed95f713e6d98ab52c のものを改造して利用している
3-2-4. エージェント型 クラス
class エージェント型:
def __init__(self, 環境, 手): #...
# properties...
def 行動する(self): #...
def 学習する(self, 報酬): #...
def 行動を選ぶ(self, 探索率 = 探索率): #...
def 状態を調べる(self): #...
def 距離と向きを調べる(self, 相手): #...
エージェントを表すクラスであり、 $Q$テーブルを持つ。
3-2-4-1. コンストラクタとプロパティ
class エージェント型:
def __init__(self, 環境, 手):
self.__環境 = 環境
self.__手 = 手
self.__x = np.random.rand() * 環境.幅
self.__y = np.random.rand() * 環境.高さ
self.__方向 = np.random.choice(向きリスト, 1)[0]
self.__速さ = np.random.choice(速さリスト, 1)[0]
self.__Q = Qテーブル型()
self.__直前の状態 = None
self.__直前の行動 = None
self.__直前の報酬 = None
@property
def 環境(self): return self.__環境
@property
def 手(self): return self.__手
@property
def 天敵(self):
return {"グー":"パー", "チョキ":"グー", "パー":"チョキ"}[self.手]
@property
def 獲物(self):
return ({"グー", "チョキ", "パー"} - {self.手, self.天敵}).pop()
@property
def Q(self): return self.__Q
@property
def 位置(self): return np.array([self.__x, self.__y])
@位置.setter
def 位置(self, value):
(x, y) = value
self.__x = x % self.__環境.幅
self.__y = y % self.__環境.高さ
@property
def 方向(self): return self.__方向
@方向.setter
def 方向(self, value): self.__方向 = 最も近いものを選ぶ(
value % (2 * np.pi), 向きリスト
)
@property
def 速さ(self): return self.__速さ
@速さ.setter
def 速さ(self, value): self.__速さ = 最も近いものを選ぶ(value, 速さリスト)
#...
手の種類 (グー, チョキ, パー) を引数にて決定している。
また初期位置、初期方向、初期速さ をランダムに決めている。
さらに $Q$テーブルを初期化している。
また学習の都合上、直前の状態、行動、報酬を記録しておく必要があるため、
self.__直前の状態, self.__直前の行動, self.__直前の報酬 属性を定義している。
(この「都合」というのは、3-2-4-3節で解説する)
天敵プロパティと 獲物プロパティ は、自身の手プロパティに応じて、"グー", "チョキ", "パー" のいずれかに決まる。
位置 プロパティは、 代入時に 環境の幅や高さの剰余 を取る仕様になっている。これによりトーラス構造を実現しており、位置を更新する際にトーラス構造を意識して手動で剰余を取る必要がなくなっている。
方向 プロパティは、 代入時に $2\pi$の剰余を取り、さらに 向きリスト 内の最も近い値に離散化される仕様となっている。これにより、方向を更新する際に手動で離散化したり、剰余を取ったりする必要がなくなっている。
速さ プロパティは、 代入時に 速さリスト 内の最も近い値に離散化される仕様となっている。これにより、速さを更新する際に手動で離散化する必要がなくなっている。
3-2-4-2. 行動する メソッド
class エージェント型:
#...
def 行動する(self):
現在の行動 = self.行動を選ぶ()
self.方向 += 現在の行動["方向の変化"]
self.速さ += 現在の行動["速さの変化"]
self.位置 += self.速さ * np.array([
np.cos(self.方向), np.sin(self.方向)
])
# 直後のステップのために現在の行動を記録しておく
self.__直前の行動 = 現在の行動
#...
self.行動を選ぶ() メソッドにより行動を決め、自身の方向、速さ、位置を更新する。
さらに学習の都合上、選んだ行動を self.__直前の行動 属性に記録しておく
(この「都合」というのは、3-2-4-3節で解説する)
3-2-4-3. 学習する メソッド
class エージェント型:
#...
def 学習する(self, 報酬):
"""
Q(直前の状態, 直前の行動)
= (1 - 学習率) * Q(直前の状態, 直前の行動)\
+ 学習率 * (直前の報酬 + 割引残率 * Q(現在の状態, 最良の行動))
"""
現在の状態 = self.状態を調べる()
if self.__直前の状態 is None:
pass
else:
最良の行動 = self.行動を選ぶ(探索率 = 0)
old_Q_直前 = self.__Q[self.__直前の状態, self.__直前の行動]
old_Q_現在 = self.__Q[ 現在の状態, 最良の行動]
new_Q_直前 = (1 - 学習率) * old_Q_直前\
+ 学習率 * (self.__直前の報酬 + 割引残率 * old_Q_現在)
self.__Q[self.__直前の状態, self.__直前の行動] = new_Q_直前
# 直後のステップのために現在の状態と報酬を記録しておく
self.__直前の状態 = 現在の状態
self.__直前の報酬 = 報酬
#...
Q学習を行う。
本来Q学習の式は
$$Q_{t}(s_{t}, a_{t}) = (1-\alpha)Q_{t-1}(s_{t}, a_{t}) + \alpha・(r_{t} + \gamma \max_{a_{t+1}'}Q_{t-1}(s_{t+1}, a_{t+1}'))$$
であるが、今回の実験では、ステップ $t$ の時点で $s_{t+1}$を知ることが出来ない。そのため、$s,a,r$の添え字を一つ過去にずらし、
$$Q_{t}(s_{t-1}, a_{t-1}) = (1-\alpha)Q_{t-1}(s_{t-1}, a_{t-1}) + \alpha・(r_{t-1} + \gamma \max_{a_{t}'}Q_{t-1}(s_{t}, a_{t}'))$$
という更新式を利用することにする。
「学習上の都合で self.__直前の状態, self.__直前の行動, self.__直前の報酬 属性が必要になる」というのは
これらの $s_{t-1}, a_{t-1}, r_{t-1}$ の情報を利用するためである。
この更新式を分かりやすく言い換えると、
$$Q(直前の状態, 直前の行動)
\leftarrow (1 - (学習率)) \times Q(直前の状態, 直前の行動)
+ (学習率) \times ((直前の報酬) + (割引残率) \times Q(現在の状態, 最良の行動))$$
ということである。
現在の状態 というのは self.状態を調べる() メソッドにて把握し、
最良の行動 というのは self.行動を選ぶ(探索率 = 0) メソッドにて把握している。
さらに学習の都合上、
-
現在の状態をself.__直前の状態属性に記録しておく - 現在の報酬 を
self.__直前の報酬属性に記録しておく- 現在の報酬は、
学習するメソッドの引数として指定される
- 現在の報酬は、
3-2-4-4. 行動を選ぶ メソッド
class エージェント型:
#...
def 行動を選ぶ(self, 探索率 = 探索率):
if np.random.rand() < 探索率:
行動 = {
"方向の変化": np.random.choice(方向の変化リスト, 1)[0],
"速さの変化": np.random.choice(速さの変化リスト, 1)[0]
}
return 行動
else:
状態 = self.状態を調べる()
暫定最大Q値 = - np.inf
暫定最良行動たち = []
for 方向の変化 in 方向の変化リスト:
for 速さの変化 in 速さの変化リスト:
行動 = {"方向の変化": 方向の変化, "速さの変化": 速さの変化}
Q値 = self.__Q[状態, 行動]
if Q値 > 暫定最大Q値:
暫定最大Q値 = Q値
暫定最良行動たち = [行動]
elif Q値 == 暫定最大Q値:
暫定最良行動たち.append(行動)
最良行動たち = 暫定最良行動たち
最良行動 = np.random.choice(最良行動たち, 1)[0]
return 最良行動
#...
ε-greedy 法に基づいて 行動を選択する。
行動 は 表3-2-4-4-1に従う辞書である。
表3-2-4-4-1. 辞書 行動 の中身
| キー | 値 |
|---|---|
"方向の変化" |
方向の変化リスト内の任意の値 |
"速さの変化" |
速さの変化リスト内の任意の値 |
行動を選択する際、探索率 は引数として指定でき、省略された場合は ハイパーパラメータで決められた 探索率 を利用する。
探索率 の確率で、行動 をランダムに決め、
1 - 探索率 の確率で、最良の行動 を選ぶ。
最良の行動というのは、現在の状態において、最も $Q$ 値が高いような行動を意味し、
同率で最大の$Q$値を持つ行動が複数ある場合は、それらの行動 (最良行動たち) の中からランダムで 行動 を選ぶ。
探索率 引数を $0$ とすると、常に最良の行動を返すため、
これは self.学習する(報酬) メソッド内で最良の行動を特定する際に用いられる。
例題3-2-4-4-1
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), (2 * np.pi / 10)]
速さの変化リスト = [-1, 1]
とする。
今、探索率が$0$, 状態が s1 で、$Q$テーブルが表3-2-4-4-2の内容であるとき、
選ばれる 行動 を求めよう。
表3-2-4-4-2. $Q$テーブル
| 状態\行動 | 方向の変化$-2\pi/10$, 速さの変化$-1$ | 方向の変化$-2\pi/10$, 速さの変化$1$ | 方向の変化$2\pi/10$, 速さの変化$-1$ | 方向の変化$2\pi/10$, 速さの変化$1$ |
|---|---|---|---|---|
s0 |
$0$ | $-1.3$ | $0.6$ | $1$ |
s1 |
$0.2$ | $-0.4$ | $2$ | $1.2$ |
| : | : | : | : | : |
解答
表3-2-4-4-2 を見ると、現在の状態 s1 で最も価値の高い行動は、
「方向の変化$2\pi/10$, 速さの変化$-1$」であるから、
選ばれる 行動 は
{
"方向の変化": 2 * np.pi / 10,
"速さの変化": -1
}
という辞書になる。
3-2-4-5. 状態を調べる メソッド
class エージェント型:
#...
def 状態を調べる(self):
環境 = self.__環境
天敵 = [
エージェント for エージェント in 環境.エージェントたち
if エージェント.手 == self.天敵
][0]
獲物 = [
エージェント for エージェント in 環境.エージェントたち
if エージェント.手 == self.獲物
][0]
(天敵の距離, 天敵の向き) = self.距離と向きを調べる(天敵)
(獲物の距離, 獲物の向き) = self.距離と向きを調べる(獲物)
状態 = {
"天敵の距離": 最も近いものを選ぶ(天敵の距離, 距離リスト),
"天敵の向き": 最も近いものを選ぶ(天敵の向き, 向きリスト),
"獲物の距離": 最も近いものを選ぶ(獲物の距離, 距離リスト),
"獲物の向き": 最も近いものを選ぶ(獲物の向き, 向きリスト),
"速さ": self.速さ
}
return 状態
#...
環境にアクセスし、天敵や獲物の距離や向きを調べ、自分の速さの情報と合わせて 現在の状態 を返却するメソッド。
状態 は表3-2-4-5-1に従う辞書である。
表3-2-4-5-1. 辞書 状態 の中身
| キー | 値 |
|---|---|
"天敵の距離" |
距離リスト内の任意の値 |
"天敵の向き" |
向きリスト内の任意の値 |
"獲物の距離" |
距離リスト内の任意の値 |
"獲物の向き" |
向きリスト内の任意の値 |
"速さ" |
速さリスト内の任意の値 |
例題3-2-4-5-1
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), (2 * np.pi / 10)]
速さの変化リスト = [-1, 1]
とする。
天敵の距離が $32.4$, 天敵の向きが $4.4(2\pi/10)$,
獲物の距離が $12$, 獲物の向きが $2.6(2\pi/10)$,
自分の速さが $2$ のとき、
状態 を求めよう。
解答
各距離、向き、速さは状態のリストで離散化されるので、状態 は
{
"天敵の距離": 30,
"天敵の向き": 4 * (2 * np.pi / 10),
"獲物の距離": 15,
"獲物の向き": 3 * (2 * np.pi / 10),
"速さ": 2
}
となる。
3-2-4-6. 距離と向きを調べる メソッド
class エージェント型:
#...
def 距離と向きを調べる(self, 相手):
環境 = self.__環境
(相手x, 相手y) = 相手.位置
距離と角度の候補たち = []
(Ax, Ay) = self.位置
for i in range(-1, 1+1):
Bx = 相手x + i * 環境.幅
for j in range(-1, 1+1):
By = 相手y + j * 環境.高さ
距離 = float(np.sqrt((By - Ay)**2 + (Bx - Ax)**2))
角度 = np.arctan2(By - Ay, Bx - Ax)
距離と角度の候補たち.append((距離, 角度))
(距離, 角度) = sorted(
距離と角度の候補たち,
key = lambda 距離と角度: 距離と角度[0]
)[0]
向き = (角度 - self.方向) % (2 * np.pi)
return (距離, 向き)
#...
相手の距離と向きを調べる。
距離は |(相手の位置) - (自分の位置)|、
向きは ${\rm arctan2}((相手の位置) - (自分の位置)) - (自分の方向)$
を返すが、環境がトーラス構造であり上端と下端、左端と右端がつながっているために、相手の位置が複数考えられることに注意が必要である。
環境の幅だけ相手の$x$座標をずらして(or ずらさず)考える3通りと、
環境の高さだけ相手の$y$座標をずらして(or ずらさず)考える3通り
を組み合わせて、相手の位置の候補を9通り考え、それらのうち距離が最短となるものを「相手の位置」とみなして、相手の距離と向きを返却する。
3-2-5. Qテーブル型 クラス
class Qテーブル型:
def __init__(self): #...
@property
def df(self): #...
def __getitem__(self, key): #...
def __setitem__(self, key, value): #...
$Q$テーブルを表すクラス。
Qテーブル型オブジェクト Qに対して、
Q[状態, 行動] にアクセスされると、
Q.__getitem__(key) が呼ばれる。
ただし key は タプル(状態, 行動) となる。
また、 Q[状態, 行動] = Q値 のように代入されると、
Q.__setitem__(key, Q値) が呼ばれる。
3-2-5-1. コンストラクタ
class Qテーブル型:
def __init__(self):
self.__ndarray = np.zeros((
len(距離リスト), len(向きリスト), len(距離リスト), len(向きリスト),
len(速さリスト),
len(方向の変化リスト), len(速さの変化リスト)
))
#...
self.__ndarray 属性により、7次元配列として $Q$テーブルを管理している。7次元はそれぞれ
- 状態を表す5次元
- 天敵の距離 (サイズ
len(距離リスト)) - 天敵の向き (サイズ
len(向きリスト)) - 獲物の距離 (サイズ
len(距離リスト)) - 獲物の向き (サイズ
len(向きリスト)) - 自分の速さ (サイズ
len(速さリスト))
- 天敵の距離 (サイズ
- 行動を表す2次元
- 方向の変化 (サイズ
len(方向の変化リスト)) - 速さの変化 (サイズ
len(速さの変化リスト))
に対応する。
- 方向の変化 (サイズ
各状態, 行動 の $Q$ 値は
self.__ndarray[
距離リスト.index(状態["天敵の距離"]),
向きリスト.index(状態["天敵の向き"]),
距離リスト.index(状態["獲物の距離"]),
向きリスト.index(状態["獲物の向き"]),
速さリスト.index(状態["速さ"]),
方向の変化リスト.index(行動["方向の変化"]),
速さの変化リスト.index(行動["速さの変化"])
]
に格納される。
初期値はすべて$0$としたいため、numpyの np.zeros を用いている。
例題3-2-5-1-1
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), (2 * np.pi / 10)]
速さの変化リスト = [-1, 1]
とする。
状態 = {
"天敵の距離": 30,
"天敵の向き": 4 * (2 * np.pi / 10),
"獲物の距離": 15,
"獲物の向き": 3 * (2 * np.pi / 10),
"速さ": 2
}
行動 = {
"方向の変化": 2 * np.pi / 10,
"速さの変化": -1
}
のとき、対応する$Q$値を、 self.__ndarray を用いて表してみよう。
解答
対応する $Q$値は
self.__ndarray[
距離リスト.index(状態["天敵の距離"]),
向きリスト.index(状態["天敵の向き"]),
距離リスト.index(状態["獲物の距離"]),
向きリスト.index(状態["獲物の向き"]),
速さリスト.index(状態["速さ"]),
方向の変化リスト.index(行動["方向の変化"]),
速さの変化リスト.index(行動["速さの変化"])
]
つまり
self.__ndarray[
距離リスト.index(30),
向きリスト.index(4 * (2 * np.pi / 10)),
距離リスト.index(15),
向きリスト.index(3 * (2 * np.pi / 10)),
速さリスト.index(2),
方向の変化リスト.index(2 * np.pi / 10),
速さの変化リスト.index(-1)
]
なので、 self.__ndarray[4, 4, 1, 3, 2, 1, 0] となる。
3-2-5-2. df プロパティ
class Qテーブル型:
#...
@property
def df(self): # メモリ不足に注意
全組み合わせ = list(itertools.product(
距離リスト, 向きリスト, 距離リスト, 向きリスト, 速さリスト,
方向の変化リスト, 速さの変化リスト
))
Q値たち = self.__ndarray.flatten()
df_ = pd.DataFrame(全組み合わせ, columns=[
"天敵の距離", "天敵の向き", "獲物の距離", "獲物の向き",
"自分の速さ",
"方向の変化", "速さの変化"
])
df_["Q値"] = Q値たち
return df_
#...
$Q$テーブルを pandas の pd.DataFrame 型データフレームに変換する。
データフレームのカラムは
"天敵の距離""天敵の向き""獲物の距離""獲物の向き""自分の速さ""方向の変化""速さの変化""Q値"
となる。
変換ロジックに itertools.product を用いているため、場合によってはメモリ不足に陥るので要注意。
3-2-5-3. __getitem__, __setitem__ 特殊メソッド
class Qテーブル型:
#...
def __getitem__(self, key):
(状態, 行動) = key
return self.__ndarray[
距離リスト.index(状態["天敵の距離"]),
向きリスト.index(状態["天敵の向き"]),
距離リスト.index(状態["獲物の距離"]),
向きリスト.index(状態["獲物の向き"]),
速さリスト.index(状態["速さ"]),
方向の変化リスト.index(行動["方向の変化"]),
速さの変化リスト.index(行動["速さの変化"])
]
def __setitem__(self, key, value):
(状態, 行動) = key
self.__ndarray[
距離リスト.index(状態["天敵の距離"]),
向きリスト.index(状態["天敵の向き"]),
距離リスト.index(状態["獲物の距離"]),
向きリスト.index(状態["獲物の向き"]),
速さリスト.index(状態["速さ"]),
方向の変化リスト.index(行動["方向の変化"]),
速さの変化リスト.index(行動["速さの変化"])
] = value
Qテーブル型オブジェクト Q に対して、 Q[状態, 行動] へのアクセスおよび代入を可能にしている。
3-2-6. 最も近いものを選ぶ 関数
def 最も近いものを選ぶ(値, 配列):
idx = np.abs(np.array(配列) - 値).argmin()
return 配列[idx]
本来連続量である状態、行動を、3-2-2節のリストにある選択肢に離散化する関数。
例えば 速さリスト = [0, 1, 2, 3, 4] で 最も近いものを選ぶ(2.6, 速さリスト) とすると、 3が返却される。
3-2-7. imscatter 関数
def imscatter(x, y, image, ax=None, zoom=1):
try: len(x)
except: x = [x]
try: len(y)
except: y = [y]
if ax is None:
ax = plt.gca()
try:
image = plt.imread(image)
except:
pass
im = OffsetImage(image, zoom=zoom)
artists = []
for x0, y0 in zip(x, y):
ab = AnnotationBbox(im, (x0, y0), xycoords='data', frameon=False)
artists.append(ax.add_artist(ab))
return (artists, im)
https://qiita.com/sabopy/items/b4ed95f713e6d98ab52c にあったものを改造。
環境のスナップショットの作成に使っている matplotlib では、画像をプロットするのが簡単にできないため、
この関数を利用している。
3-2-8. メインコード
環境 = 環境型()
for _ in range(2002189): # ここは適当にいじる
環境.ステップを進める()
環境型 オブジェクトを作り、$2002189$ 回だけ ステップを進める メソッドを呼び出すことで、シミュレーションを$2002189$ ステップ実行している。
$2002189$ という数字については、筆者が使っている GIF アニメライターが 最大で$8189$枚の静止画しか読み込めないため、それにステップ数を合わせた都合で決めた。
読者が実験する際は当然自由に変更してよい。
3-3. 実験1
まずは ./base.py のハイパーパラメータ、状態と行動のリストを次のように変更した ./実験1.py を実行してみた。
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 10
目標速さ = 1
環境の幅 = 250
環境の高さ = 250
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), 0, (2 * np.pi / 10)]
速さの変化リスト = [-2, -1, 0, 1, 2]
すると、次のような結果となった。
動画3-3-1. 実験1の結果
speed (グー, チョキ, パー) は、それぞれグー、チョキ、パーのエージェントの速さを表している。
速さについては $100000$ ステップごろから、目標速さ $1$ に近い値をとるようになっている。
一方、追いかけたり逃げたりの「鬼ごっこ」のような挙動は、$300000$ ステップごろまで目立たなかった。
また、$300000$ ステップごろにおいても、互いにある程度(距離$50$程度)接近したときだけ、
逃げたり追いかけたりする挙動が確認できた。 ($300233~300255$ ステップ, 図3-3-1)
図3-3-1. 距離が近いときに見られた鬼ごっこのGIFアニメ
その後、 $1000193~1000299$ステップ、$1100000~1100140$ステップ、 $1200202~1200252$ でパーがグーを追いかけて捕まえたり、
$1100144~1100163$ステップでグーがチョキを追いかけて捕まえたり、
$1400000~1400157$ステップでチョキがパーを追いかけて捕まえたりする挙動が確認できた。
追いかけたり逃げたりするときは、目標速さを無視して可能な最大速さ$4$に近い速さで移動していた。(図3-3-2)
これらは、やはり互いにある程度接近した時のみに確認できる挙動で、長期的な利害を考えて敵や獲物が遠くにいるうちから行動するような挙動は$1300000$ステップごろまでは見られなかった。
図3-3-2. 距離が近いときに見られた鬼ごっこのGIFアニメ2
しかし、 $1400000$ステップごろになると、敵や獲物が遠くにいるうちから、速さ1で逃げたり追いかけたりする挙動も確認できた。
例えば、 $1400196~1400299$ステップでは、チョキは速さ$1$でパーを追いかけ、パーは速さ$1$でチョキから逃げつつグーを追いかけ、パーは速さ$1$でグーから逃げていたし、
$1500000~1500140$ステップでも、各エージェントは速さ$1$で天敵から逃げつつ、獲物を追いかけていた。(図3-3-3)
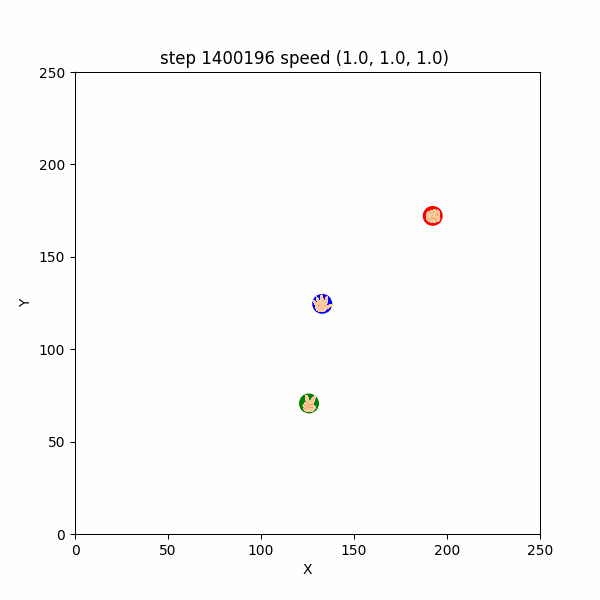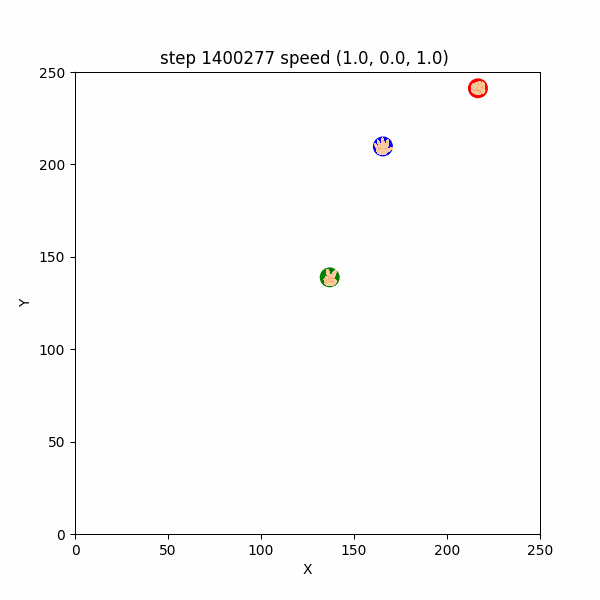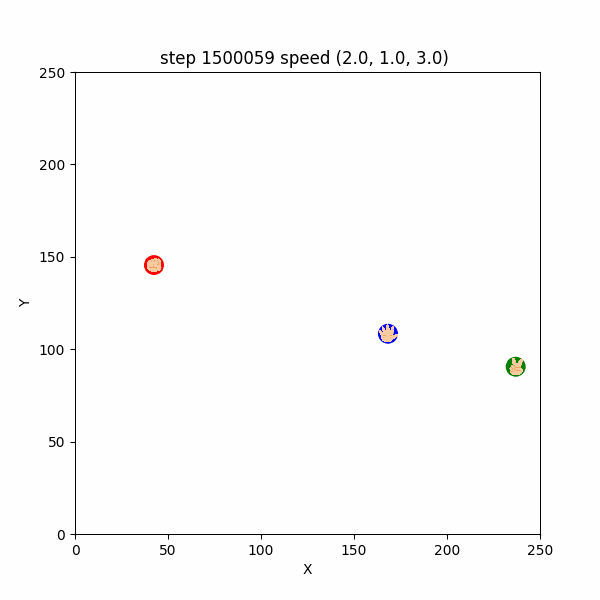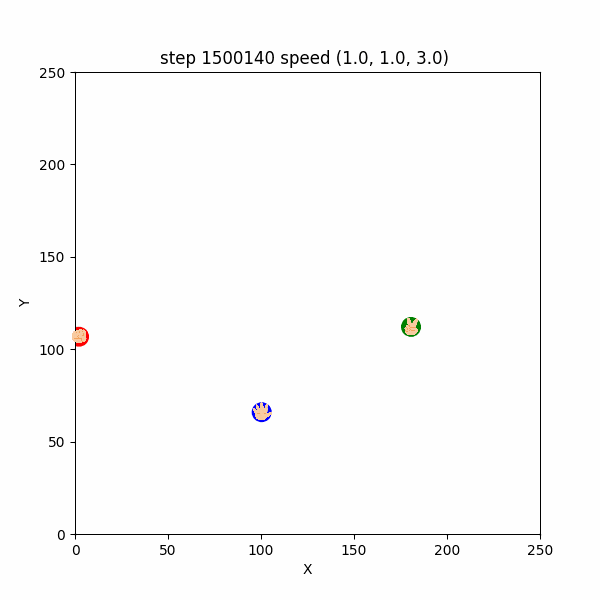
図3-3-3. 距離が遠いときの速さ1での鬼ごっこのGIFアニメ
一方残念なことに、$1600000$ステップごろにおいても、合理的ではなさそうな挙動をするエージェントが確認できた。
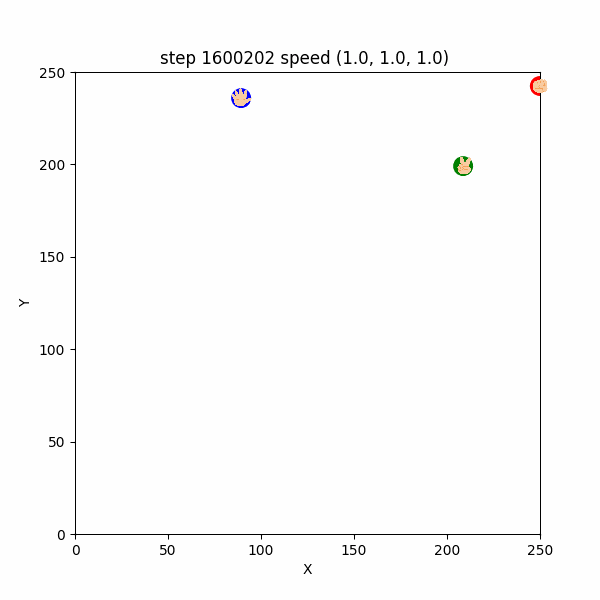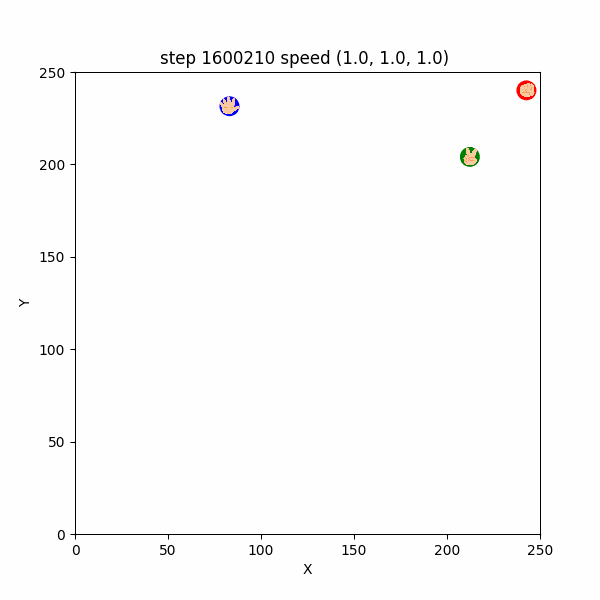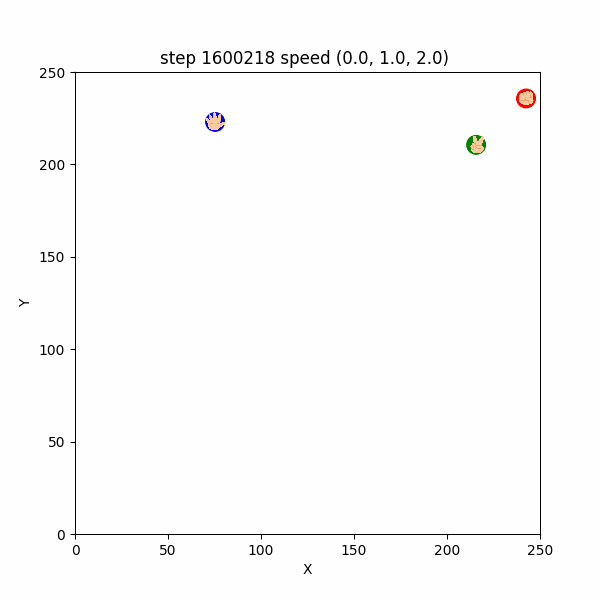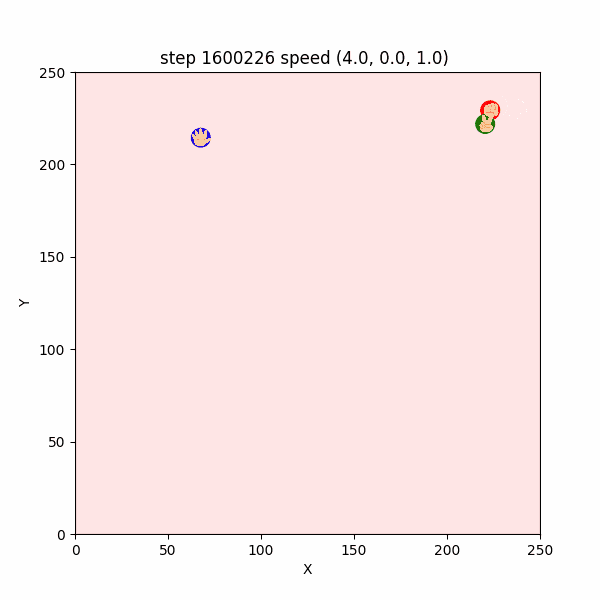
例えば、$1600202~1600226$ においては、チョキが天敵であるグーを速さ$3$程度で追いかけた挙句、グーに捕まる「自爆」をしていた。(図3-3-4)
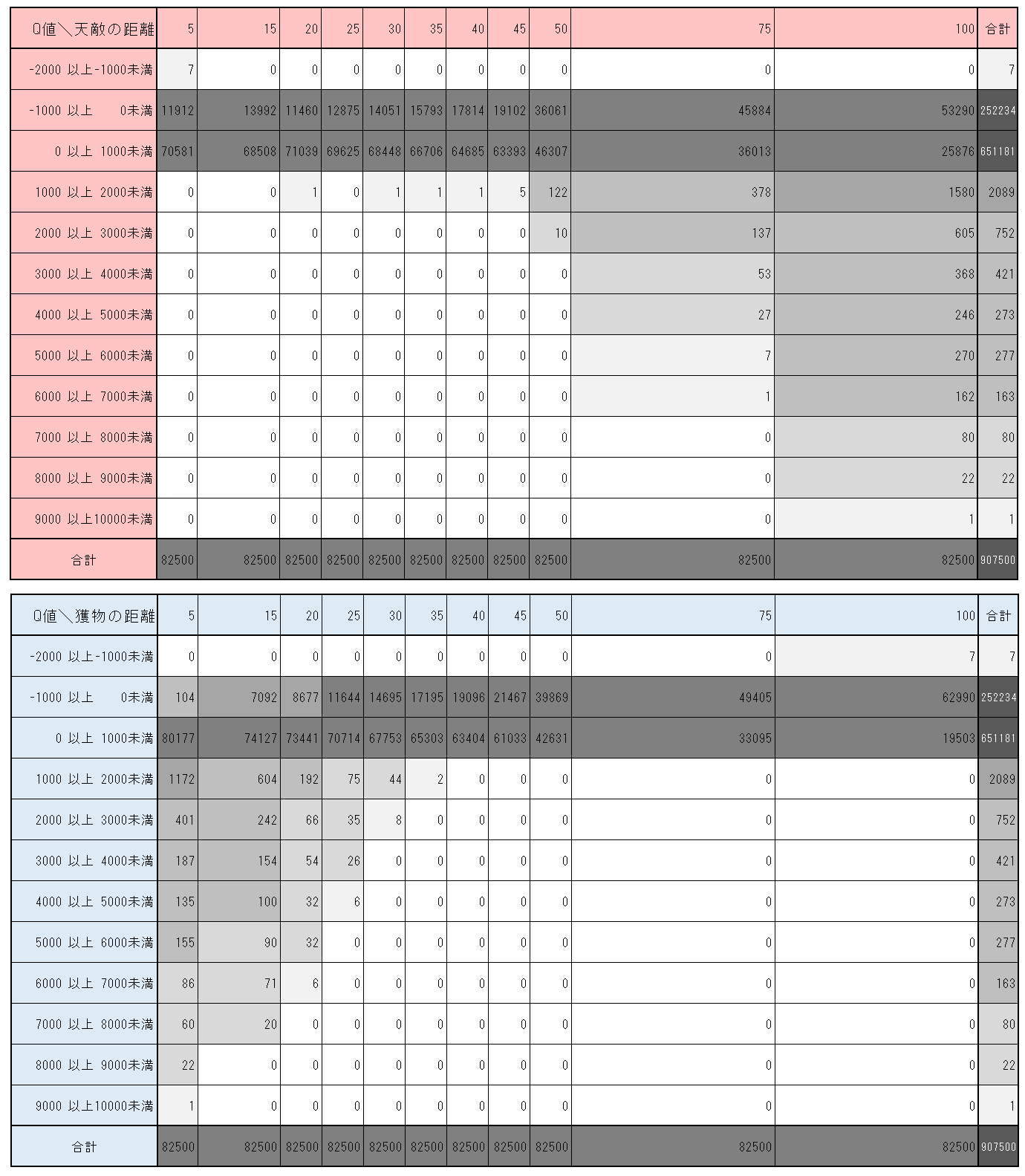
$1600000$ステップにおけるチョキの$Q$テーブルから、天敵や獲物の距離ごとの$Q$値度数分布表を作ると、
図3-3-5 のようになる。
図3-3-5. $1600000$ステップにおけるチョキの$Q$値の度数分布表
図3-3-5から、天敵との距離が遠い状態ほど、また獲物との距離が近い状態ほど、大きな価値を持つことが学習されていることがわかる。また階級からも分かる通り、$Q$値の最小値は $-2000$ 以上 $-1000$未満の範囲にあり、最大値は$9000$以上、$10000$未満の範囲にあることが分かる。このことから、チョキは天敵に捕まる経験よりも、獲物を捕まえる経験を多くしているのではないかと推察できる。$1600202~1600226$ における「自爆」は、天敵に捕まり、負の報酬を受ける経験の不足から来ているのではないかと考えられる。
さらに、$1600000$ステップにおけるチョキの$Q$テーブルから、天敵や獲物の向きごとの各行動の平均$Q$値をまとめたものが 図3-3-6である。
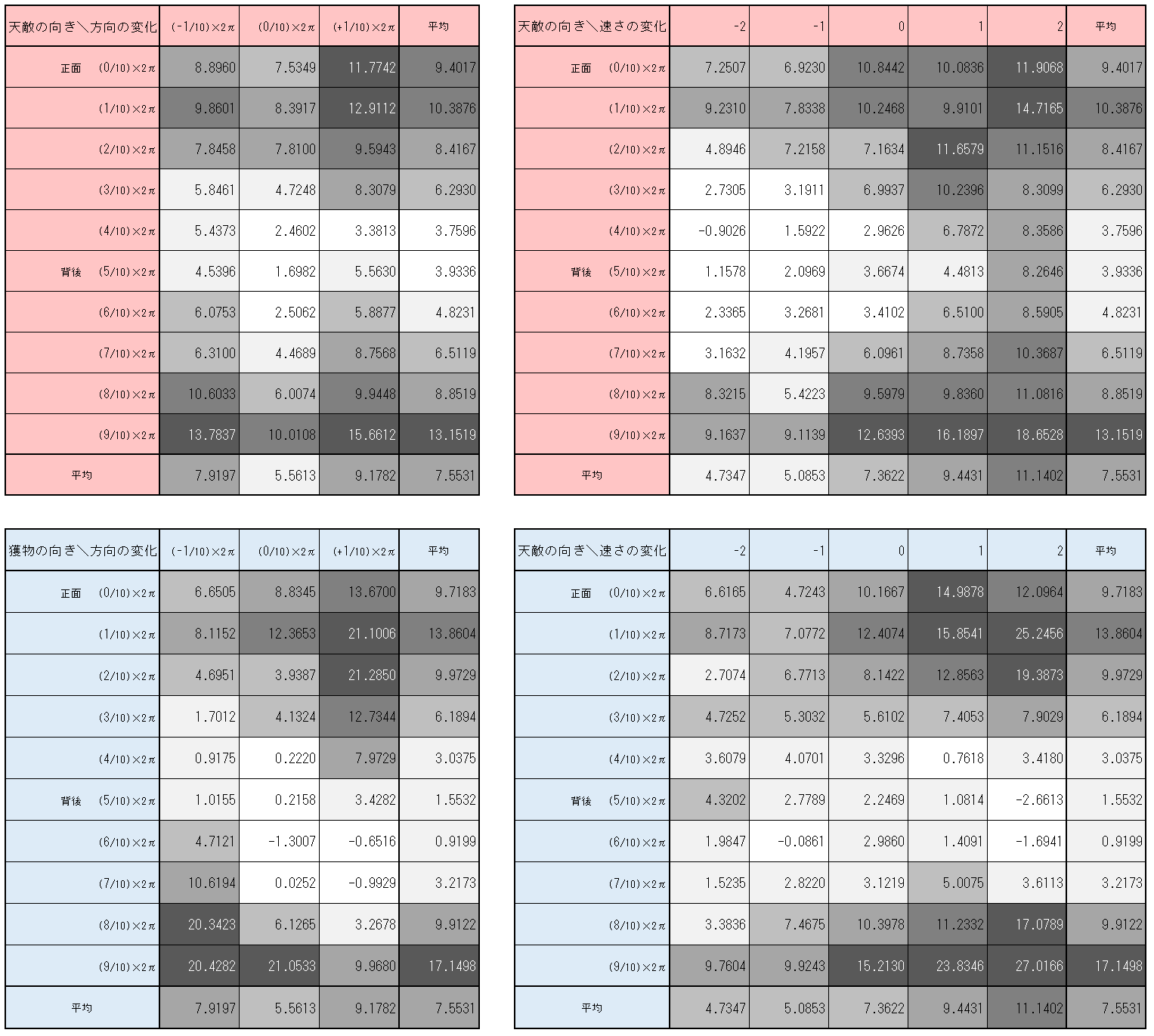
図3-3-6. $1600000$ステップにおけるチョキの$Q$値の平均(天敵や獲物の向き、および行動毎)
図3-3-6 から次のことが分かる。
- 天敵や獲物の向きと $Q$値の関係について
- 天敵や獲物が正面にいる場合の平均$Q$値は大きく、
背面にいる場合の平均$Q$値は低い
- 天敵や獲物が正面にいる場合の平均$Q$値は大きく、
- 行動 (方向の変化) について
- 天敵や獲物が正面または背面にいる場合は、方向を変化させない行動の$Q$値が低い傾向にある
- 獲物が斜めを向いている場合は、獲物の方向を向く行動の$Q$値が高い傾向にある
- 獲物が$(1/10)\times2\pi$ の向きにいる時、方向の変化を 獲物と同じ $+(1/10)\times2\pi$ とする$Q$値 ($21.1006$) が最も高く、
次いで方向を変えない $Q$値 ($12.3653$), 反対方向の $Q$値 ($8.1152$) となっている。 - 獲物が$(9/10)\times2\pi$ つまり$-(1/10)\times2\pi$の向きにいる時、方向の変化を 獲物と同じ $-(1/10)\times2\pi$ とする$Q$値 ($20.4282$) や、
向きを変えない $Q$ 値 ($21.0533$) が大きく、反対方向の $Q$ 値は $9.9680$ と、小さくなっている。
- 獲物が$(1/10)\times2\pi$ の向きにいる時、方向の変化を 獲物と同じ $+(1/10)\times2\pi$ とする$Q$値 ($21.1006$) が最も高く、
- 上記の傾向、あるいはその逆は、天敵に対しては確認できなかった
- 行動 (速さの変化) について
- 天敵や獲物が正面にいるときは、加速する行動の $Q$値が大きかった
- 天敵が背後にいるときは、加速する行動の$Q$値が大きかった
- 獲物が背後にいるときは、減速する行動の$Q$値が大きかった
「獲物の方向を向くと$Q$値が大きくなる」ことが学習できている一方、「天敵の方向を向くと$Q$値が小さくなる」ことが学習できていないこと、
また天敵が正面を向いていても$Q$値が大きく、そのまま加速する行動の$Q$値が大きかったことにより、「天敵に近寄ったら損をする」ことを充分学習できていないことが定量的に確認できた。そのために、図3-3-4でみられたような「自爆」が起きるものと考えられる。
図3-3-7 は、天敵や獲物の距離ごとに平均$Q$値をまとめたものである。図3-3-7からも、天敵が距離$5$以外で近くにいてもあまり低い$Q$値にならないことが確認できる。(獲物の距離が平均的であるとき、天敵が距離$15$にいようと$45$にいようと、$Q$値はほぼ変わらず$-0.5$付近にある)
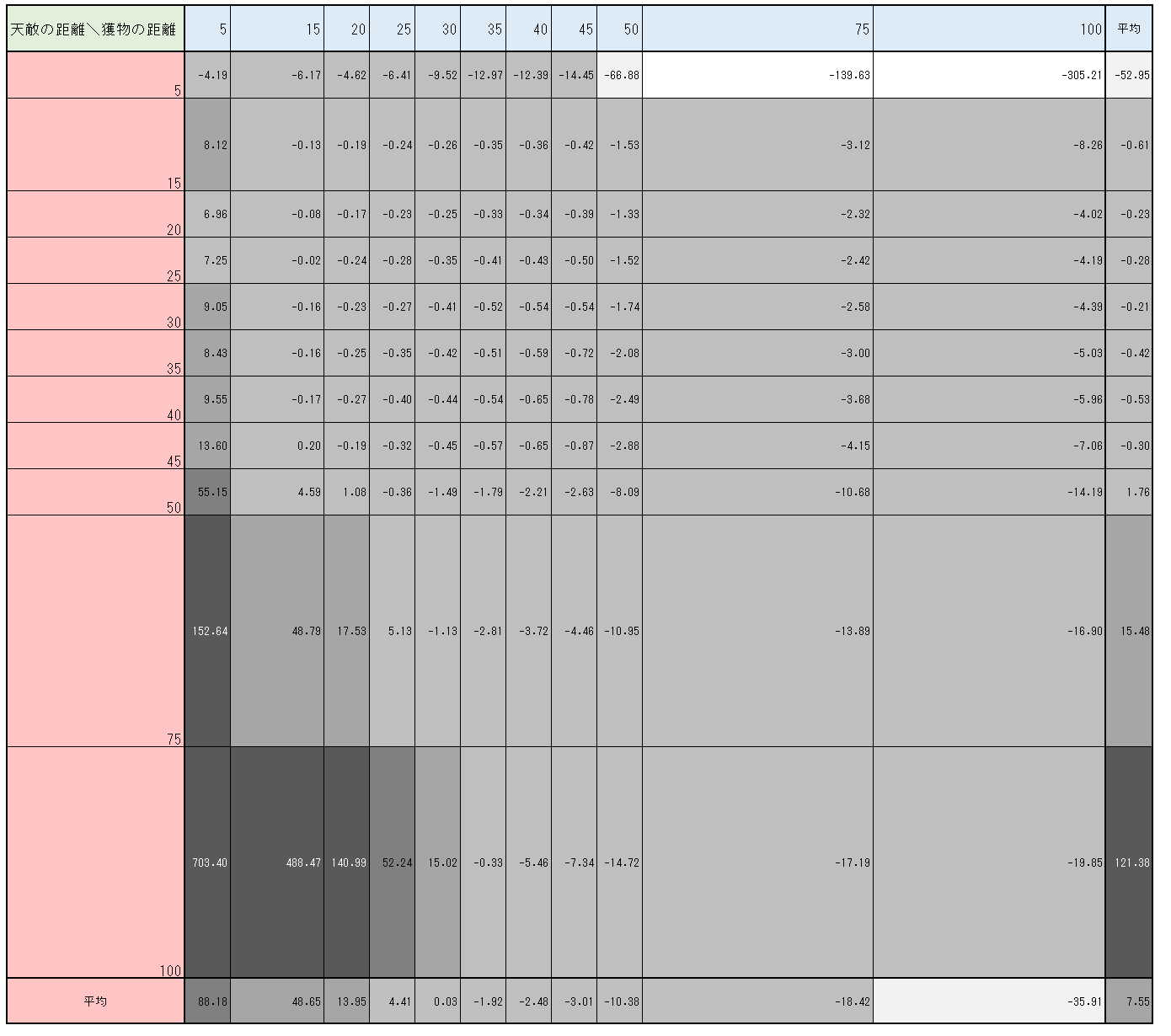
図3-3-7. $1600000$ステップにおけるチョキの$Q$値の平均(天敵や獲物の距離毎)
最後に、現在の速さと速さの変化ごとに平均$Q$値をまとめたものが図3-3-8である。
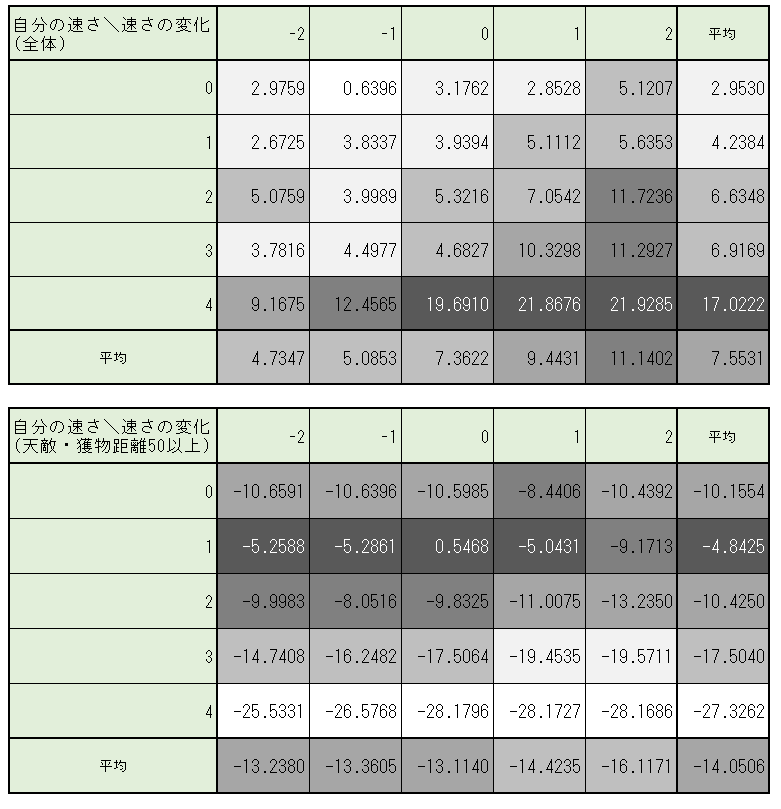
図3-3-8. $1600000$ステップにおけるチョキの$Q$値の平均(速さおよび速さの変化毎)
これは 「目標速さ」に拘わらず、獲物を大きい速さで追いかけることにより、より大きな報酬が貰えるためと考えられる。
(あるいは、天敵から大きい速さで逃げることにより、負の報酬を避けていると考えられる。)
天敵・獲物の距離$50$以上という条件を付けた表をみると、
今度は速さが$1$に近いほど$Q$値が大きくなっている。
また、速さを$1$に調整する行動ほど、$Q$値が大きくなっている。
- 速さが $0$ のとき、 速さの変化 $1$ が最大$Q$値となっている
- 速さが $1$ のとき、 速さの変化 $0$ が最大$Q$値となっている
- 速さが $2~4$ のとき、 速さの変化 $-1$ が最大$Q$値となっている
3-4. 実験2
実験1の結果では、チョキについて、獲物(パー)を追うことはよく学習できたことに比べて、
天敵(グー)から逃げることはあまりよく学習できていなかった。
これは、目標速さが小さすぎて、エージェント同士が慎重に距離を確保しやすくなったため、触れたり触れられたりする機会が少なかったためでないかと考えた。
そこで、実験2では、目標速さを最大値である$4$に変更してやりなおしてみた。
具体的には ./base.py のハイパーパラメータ、状態と行動のリストを次のように変更した ./実験2.py を実行してみた。
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 10
目標速さ = 4 # 実験1からの変更点
環境の幅 = 250
環境の高さ = 250
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), 0, (2 * np.pi / 10)]
速さの変化リスト = [-2, -1, 0, 1, 2]
すると、次のような結果となった。
動画3-4-1. 実験2の結果
速さについては、$200000$ ステップごろから目標速さ$4$に近づく傾向があったが、このころはノイズが大きかった。$500000$ステップごろになると、ノイズ(速さが$4$以外になること)が少し減ったようだった。
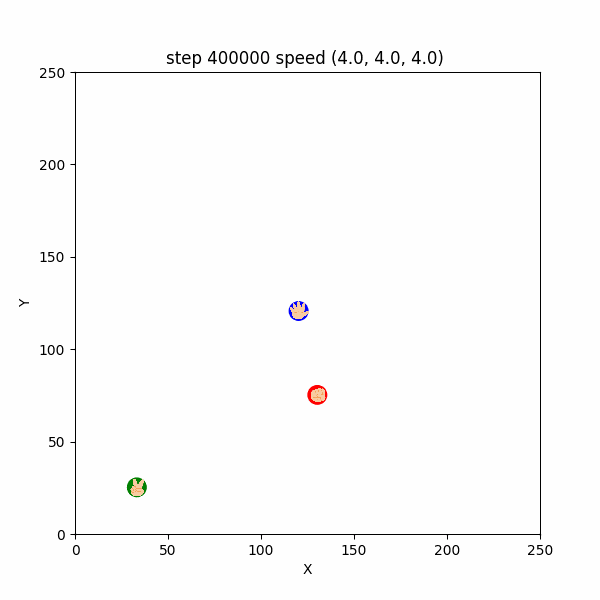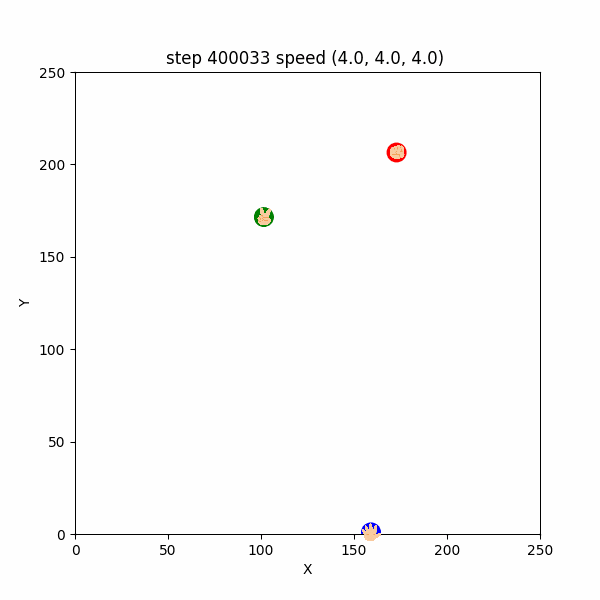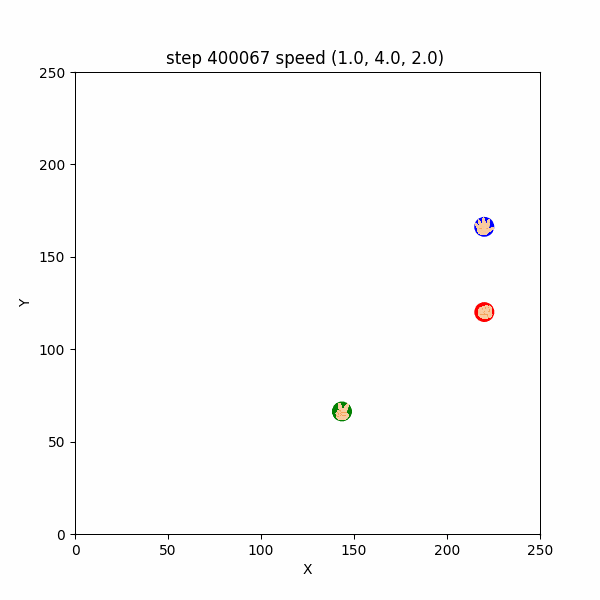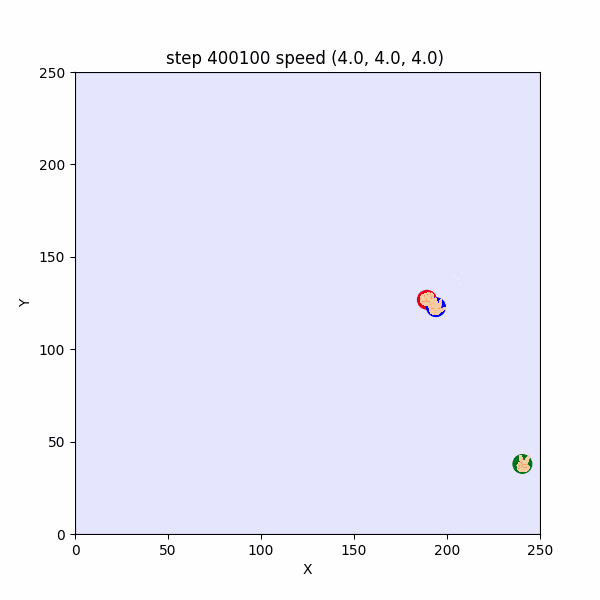
長期的な追いかけっこの挙動は $400000$ステップごろから確認出来て、このころは直線的な移動が多かった。(図3-4-2)
また、$700000$ステップごろになると、Uターンして方向を変えるなど、工夫した動きも見られた。
例えば$700120~700150$ステップでは、グーがUターンしている。(図3-4-3)
おそらくこれは、$700130$ステップまでは、トーラス構造の最短距離を考慮するとパーがグーの右上の方向にいたため、左下へ逃げていたところ、$700130$ステップ以降は最短距離でパーがグーの左下にいる形となったため、右上に引き返したものと考えられる。
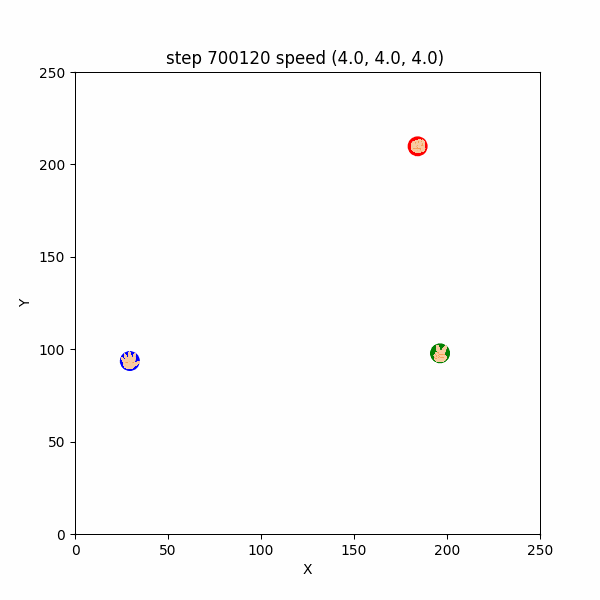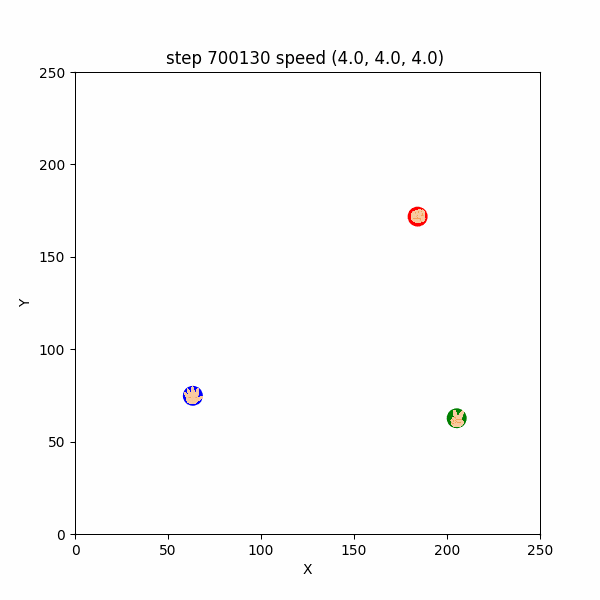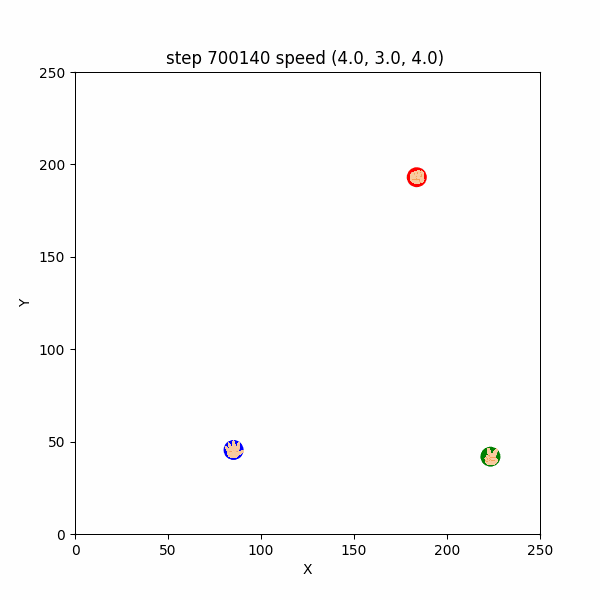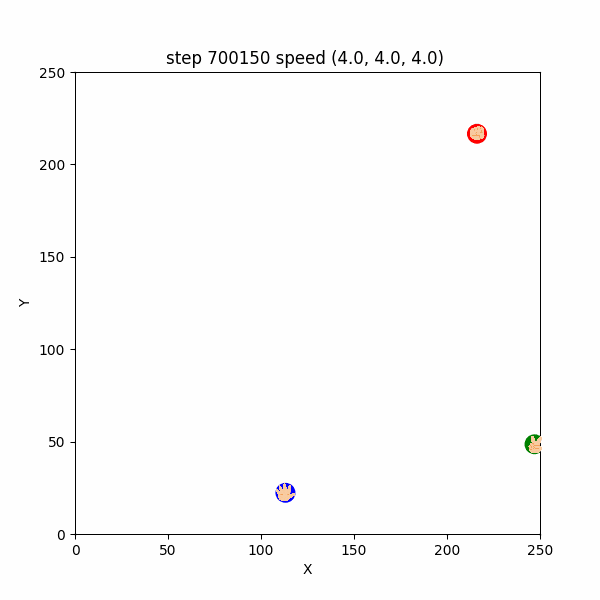
図3-4-3. グーがUターンしてパーから逃げるGIFアニメ
さらに、$1300000$ステップ以降では、回転しながら追いかけっこする挙動も見られた。(図3-4-4)
例えば $1300145~1300299$, $1600045~1600299$, $2000000~2000600$ステップなど。
また、実験1の図3-3-7と比較するため、実験2の$1600000$ステップにおけるチョキの$Q$値をまとめたものが図3-4-5である。
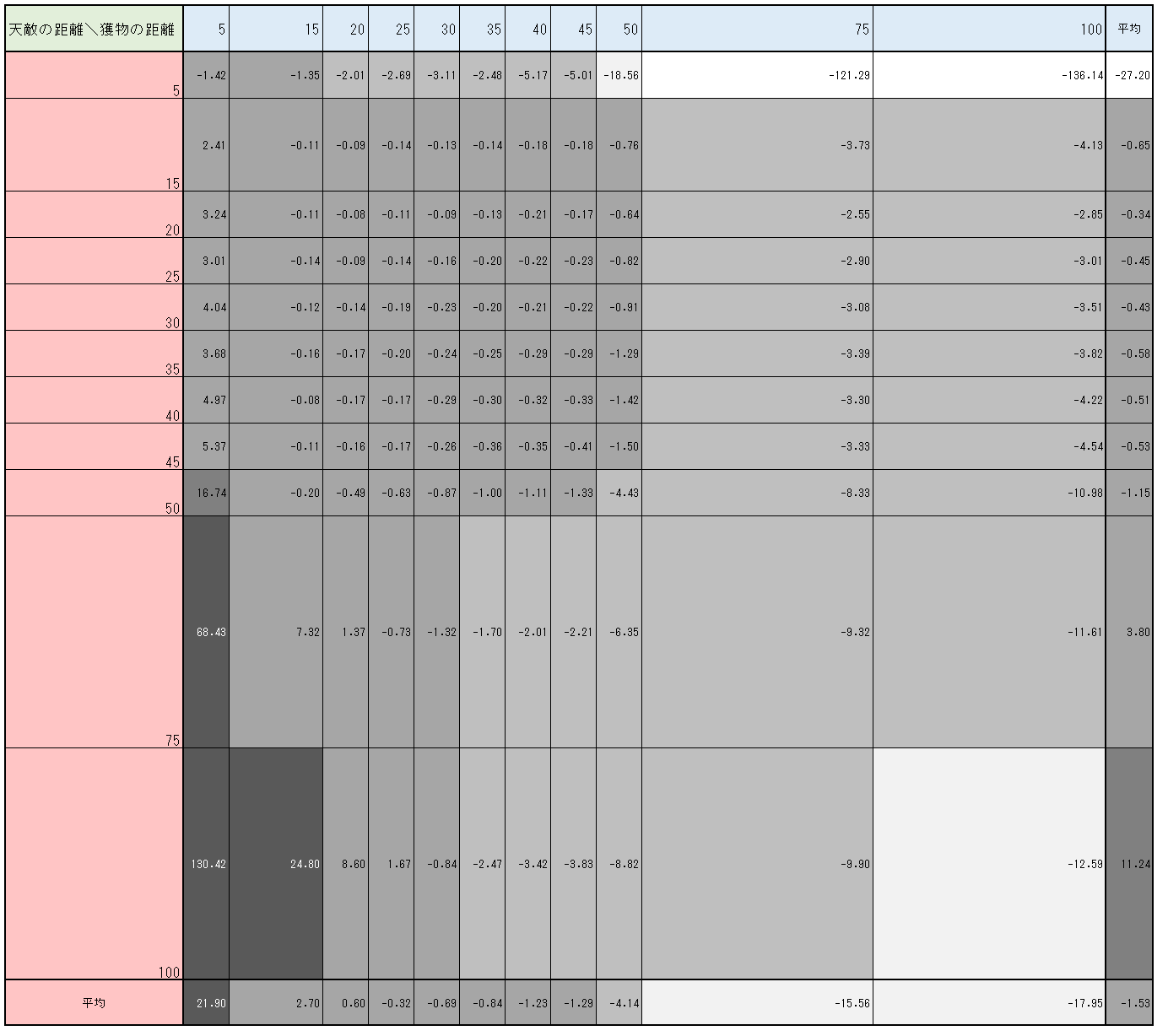
図3-4-5. $1600000$ステップにおけるチョキの$Q$値の平均(天敵や獲物の距離毎)
天敵が距離$5$以外で近くにいてもあまり低い$Q$値にならないのは、実験1と同様だった。
また、目標速さが速さの最大値である$4$である今回、基本的には減速したり等速での行動を選んだりする動機はなく、加速する行動を選び続けるはずである。しかし実際には、時々減速する行動が観察されている。
そこで、$1600000$ステップにおけるチョキの$Q$値について、天敵や獲物の距離の状態および加減速の行動毎にまとめた図3-4-6を作成してみた。
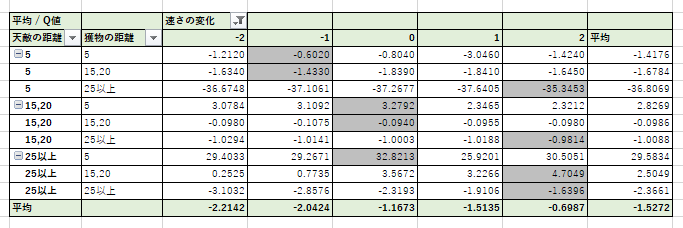
図3-4-6. $1600000$ステップにおけるチョキの$Q$値の平均(天敵や獲物の距離および速さの変化毎)
図3-4-6から、 天敵と獲物の両方が近くにいるときは減速、どちらか一方のみが近くにいるときは等速、それ以外は加速の行動が選ばれる傾向にあることが確認できた。
おそらく、
天敵が近くにいるときは、敢えて減速することで天敵を自分を追い越させることで、
自分を見失わせようとしており、
逆に獲物が近くにいるときは、獲物を見失わないように速さを落としているのではないだろうか。
3-5. 実験3
実験3では、速さ報酬係数を$0$とし、さらにパーを中央に固定し、動かなくさせてみた。
パーを動かなくすることで、チョキは「追いかける」ことを効率よく学習し、またグーは「逃げる」ことを効率よく学習するはずである。
また、ある程度学習が進むと、チョキは動かない獲物であるパーに重なって静止するものと考えられる。この場合、グーは「常に天敵(パー)に触れている獲物(グー)を如何にして捉えるか」というジレンマを抱えることになる。このジレンマをどう乗り越えるかが実験3の最大の見どころであると言っていいだろう。
まず、 ./base.py を複製し、 エージェント型のコンストラクタと 行動を選ぶ メソッドを次のように改修した ./pa_stop.py を作成した。
#...
class エージェント型:
def __init__(self, 環境, 手):
self.__環境 = 環境
self.__手 = 手
self.__x = np.random.rand() * 環境.幅
self.__y = np.random.rand() * 環境.高さ
self.__方向 = np.random.choice(向きリスト, 1)[0]
self.__速さ = np.random.choice(速さリスト, 1)[0]
self.__Q = Qテーブル型()
self.__直前の状態 = None
self.__直前の行動 = None
self.__直前の報酬 = None
# pa_stop.py ここから追加
if 手 == "パー":
self.__x = 環境.幅 / 2
self.__y = 環境.幅 / 2
self.__速さ = 0
# pa_stop.py ここまで追加
#...
def 行動を選ぶ(self, 探索率 = 探索率):
# pa_stop.py ここから追加
if 手 == "パー":
return {
"方向の変化": 最も近いものを選ぶ(0, 方向の変化リスト),
"速さの変化": 最も近いものを選ぶ(0, 速さの変化リスト)
}
# pa_stop.py ここまで追加
if np.random.rand() < 探索率:
行動 = {
"方向の変化": np.random.choice(方向の変化リスト, 1)[0],
"速さの変化": np.random.choice(速さの変化リスト, 1)[0]
}
return 行動
else:
状態 = self.状態を調べる()
暫定最大Q値 = - np.inf
暫定最良行動たち = []
for 方向の変化 in 方向の変化リスト:
for 速さの変化 in 速さの変化リスト:
行動 = {"方向の変化": 方向の変化, "速さの変化": 速さの変化}
Q値 = self.__Q[状態, 行動]
if Q値 > 暫定最大Q値:
暫定最大Q値 = Q値
暫定最良行動たち = [行動]
elif Q値 == 暫定最大Q値:
暫定最良行動たち.append(行動)
最良行動たち = 暫定最良行動たち
最良行動 = np.random.choice(最良行動たち, 1)[0]
return 最良行動
#...
#...
エージェントの手がパーである場合、
- 初期は中央に配置し、速さ$0$とすればよい →
エージェント型のコンストラクタで実現 - 各行動で、速さの変化を$0$とすればよい →
エージェント型の行動を選ぶメソッドで実現
次に ./pa_stop.py のハイパーパラメータ、状態と行動のリストを次のように変更した ./実験3.py を実行してみた。
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 0 # 実験2からの変更点
目標速さ = 4
環境の幅 = 250
環境の高さ = 250
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), 0, (2 * np.pi / 10)]
速さの変化リスト = [-2, -1, 0, 1, 2]
すると、次のような結果となった。
動画3-5-1. 実験3の結果
$300000~300126$ ステップでは、グーが敢えてパー付近に待機し、チョキがパーを捕まえようと接近してくるのを待ち構えるような挙動が確認できた。(図3-5-2)
図3-5-2. チョキを待ち伏せするチョキを待ち伏せするグーのGIFアニメ
その後、$400000$ステップ以降は、例えば図3-5-3のように、チョキがパーに張り付いて、「盾」のようにパーを利用し、
グーがチョキに接近できないという状態がほぼずっと続くだけだった。
グーはパーやチョキからある程度距離を離れたところをぐるぐる回るだけで、
「パーを避けつつチョキに接近する」とか、「パーを突破してチョキに無理やり触れる」といったような挙動は確認できなかった。
図3-5-3. パーを盾にグーから隠れるチョキのGIFアニメ
今回、グーがチョキを捕まえる挙動が出来なかった理由を考えてみる。
まずグーが「パーを盾にして隠れているチョキに触れる」ためには、次のA, B どちらかの挙動をしなければならない
- A. パーを避けつつチョキに触れる
- B. パーを突破してチョキにも触れる
Aについては、「パーを避けてチョキに触れる」ためにグーが動く距離よりも、
「パーがグーに対する盾になる向きに移動する」ためにチョキが動く距離のほうがはるかに短いため、
グーとチョキがどちらも同程度に合理的な振る舞いをする場合、Aの実現は現実的ではない。
Bについては、Bという挙動にトータルで正の価値がなければならない。
つまり、パーを突破することによる負の報酬よりも、その直後にチョキに触れることによる正の報酬のほうが大きくなくてはならない。
今回、1ステップ当たりの「捕食報酬」は一定なので、
単にパーを突破するのにかかるステップ数よりも、その後チョキを捕まえ続けられるステップ数の期待値のほうが大きくなければならない。
しかし、チョキは動いて逃げることが出来るため、その分チョキを捕まえ続けられるステップ数の期待値は小さくなってしまう。
よって、Bという挙動にトータルで正の価値を見出すことが難しかったものと考えられる。
さらに、パーとチョキが同じ位置にいるとき、グーと(パー,チョキ)の距離は、「最大距離の半分」程度になることが期待される。
これは、グーにとって天敵パーからは最大距離を取ることに最も価値があるが、獲物チョキに対しては、距離$0$を取ることが最も価値があるため、
パーとチョキが同じ位置にいるとき、グーは最大距離と$0$の中間を取ることが期待されるためである。
3-6. 実験4
実験3では、パーとチョキが同じ位置にいるとき、グーがパーやチョキから「最大距離の半分」程度だけ距離を取るよう学習してしまった(と考えられる)ため、
グーがチョキを捕まえに行くことが無くなってしまった。
そこで、実験4 では 「最大距離の半分」を小さくすることにした。つまり環境の幅と高さを小さくした
こうすれば、偶然でもグーがチョキを捕まる可能性が高まるため、
グーがチョキを捕まえる挙動を学習する可能性が高まると考えたからだ。
具体的には ./pa_stop.py のハイパーパラメータ、状態と行動のリストを次のように変更した ./実験4.py を実行してみた。
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 0
目標速さ = 4
環境の幅 = 75 # 実験3からの変更点
環境の高さ = 75 # 実験3からの変更点
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [i * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), 0, (2 * np.pi / 10)]
速さの変化リスト = [-2, -1, 0, 1, 2]
(些細な変更もした)
環境の大きさが小さくなったことに伴い、環境型の画像を作るメソッドでスナップショットが作られる際に描画されるエージェントを表す半径5の円が大きくなる。そのため、 画像を作るメソッド内で呼ばれる imscatter関数のzoom引数を、 .05から .15 に変更し、いらすとやのじゃんけんの画像を少し拡大した。
(些細な変更 ここまで)
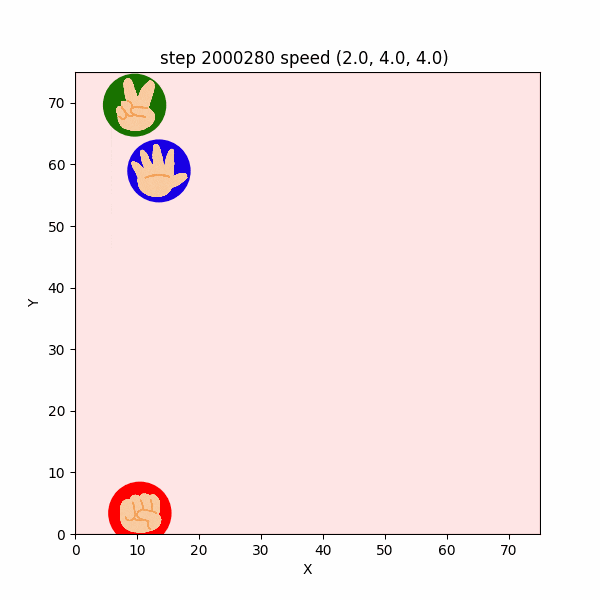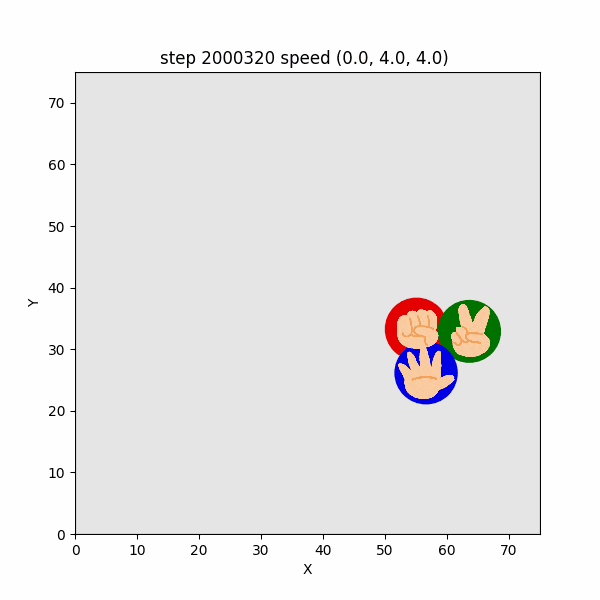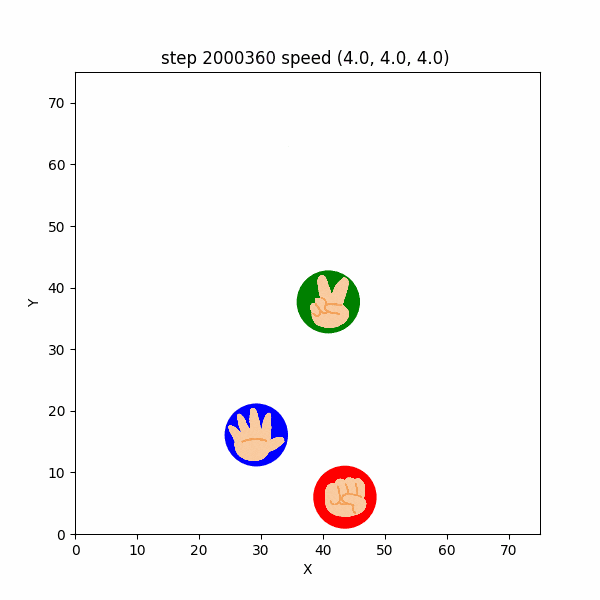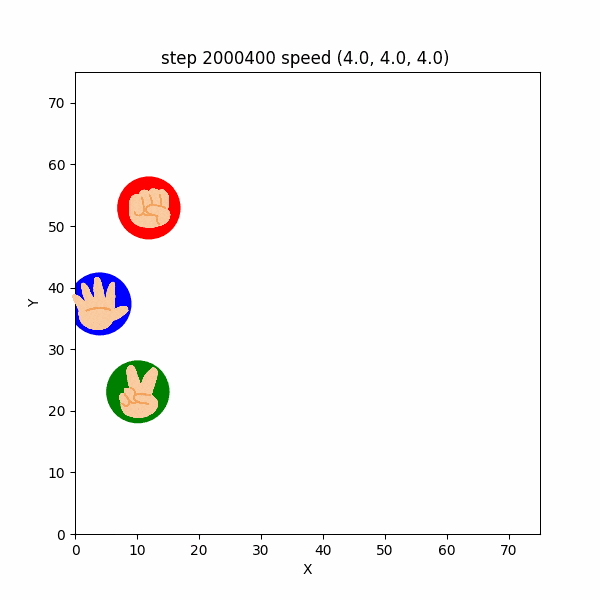
すると、次のような結果となった。
動画3-6-1. 実験4の結果例えば、図3-6-2 ($500000$ステップごろ)のように、チョキがパーを盾にしてグーから逃げつつも、時々逃げ遅れてグーに捕まる挙動が確認できた。
図3-6-2. パーを盾にしながらも時々グーに捕まるチョキのGIFアニメ
これは、環境の幅と高さが実験3と比較して小さくなったことで、グーの期待距離である「最大距離の半分」が小さくなったため、偶然でもグーがチョキを捕まる機会が増え、グーがチョキを捕まえる挙動を学習することが出来たためと考えられる。その他にも環境の大きさが小さくなったことで、「パーを避けてチョキに触れる」ためにグーが動く距離と、「パーがグーに対する盾になる向きに移動する」ためにチョキが動く距離の差が縮まったために、グーがチョキを、パーを避けつつ捕まえられる可能性が高くなったことも、グーの学習がうまくいった要因の一つと考えられる。
ただ、さらに学習を進めて $2000000$ステップごろになると、チョキがよりパーから「うまく逃げる」ようになり、グーがチョキを捕まえることがほとんどなくなった。(図3-6-3) それでも、実験3とはことなり、グーはパーすれすれの距離で執拗にチョキを追いかけ続けた。
3-7. 実験5
実験4において、グーとチョキがほとんど時計回りに動いて、反時計回りにはほとんど動いていなかったことが気になった。そこで実験5では、「時計回りに偏った実験4」が偶然なのか、それとも何らかの理由で時計回りになりやすい傾向があるのかを確かめるために、実験4と同じ実験を10回繰り返しながら、グーとチョキのパーに対する角速度をプロットしてみることにした。
3-7-1. 実験5のコードと実行
./実験4.py の
for _ in range(2002189):
環境.ステップを進める()
を、次の内容に置き換えた ./実験5.py を10回実行した。
def パーに対する向きと角速度を求める(エージェント, 位置直前, 向き直前):
"""
向きはradian, 角速度はdegree なので注意
"""
#向き = (パー.距離と向きを調べる(エージェント)[1] + パー.方向) % (2 * np.pi)
向き = パー.距離と向きを調べる(エージェント)[1]
if 向き直前 is None:
return (向き, None)
if np.linalg.norm(エージェント.位置 - 位置直前) > 環境.幅 / 2:
# 端をまたいだ場合は角速度を計算しない
return (向き, None)
角速度 = (向き - 向き直前) % (2 * np.pi)
if 角速度 > np.pi:
角速度 -= 2 * np.pi
角速度 = np.rad2deg(角速度)
return (向き, 角速度)
環境 = 環境型()
(グー向き直前, チョキ向き直前) = (None, None)
(グー位置直前, チョキ位置直前) = (None, None)
(グー角速度たち, チョキ角速度たち) = ([], [])
[グー, チョキ, パー] = 環境.エージェントたち
ステップ数 = 2002189
for _ in range(ステップ数):
環境.ステップを進める()
(グー向き, グー角速度) = パーに対する向きと角速度を求める(
グー, グー位置直前, グー向き直前
)
(チョキ向き, チョキ角速度) = パーに対する向きと角速度を求める(
チョキ, チョキ位置直前, チョキ向き直前
)
グー角速度たち += [グー角速度]
チョキ角速度たち += [チョキ角速度]
グー位置直前 = グー.位置
チョキ位置直前 = チョキ.位置
グー向き直前 = グー向き
チョキ向き直前 = チョキ向き
# 全体の角速度をプロットする。
# グー角速度とチョキ加速度を連結してシャッフルすることで、
# 特定の手のプロットが奥/手前に行かないようにしている
ステップたち = np.concatenate([np.arange(ステップ数), np.arange(ステップ数)])
角速度たち = np.concatenate([グー角速度たち, チョキ角速度たち])
色たち = np.array([[1, 0, 0]] * ステップ数 + [[0, 0.5, 0]] * ステップ数)
シャッフルindices = np.random.permutation(len(ステップたち))
ステップたち = ステップたち[シャッフルindices]
角速度たち = 角速度たち [シャッフルindices]
色たち = 色たち [シャッフルindices]
plt.close("all")
plt.figure(figsize = (16, 6))
plt.subplot(1, 2, 1)
plt.scatter(ステップたち, 角速度たち, color=色たち, alpha=0.2, s=0.01)
# plt.gca().axhline(0, color='k', alpha=0.5, zorder=-1) # 角速度0の線を引きたければコメント解除
plt.xlim(0, ステップ数)
plt.ylim(-180, 180)
plt.xlabel("step")
plt.ylabel("angular velocity [deg]")
plt.ticklabel_format(style='plain',axis="x")
plt.tight_layout()
# 最後2189ステップの角速度をプロットする
ステップたち = np.concatenate([
np.arange(ステップ数)[-2189:], np.arange(ステップ数)[-2189:]
])
角速度たち = np.concatenate([グー角速度たち[-2189:], チョキ角速度たち[-2189:]])
色たち = np.array([[1, 0, 0]] * 2189 + [[0, 0.5, 0]] * 2189)
シャッフルindices = np.random.permutation(len(ステップたち))
ステップたち = ステップたち[シャッフルindices]
角速度たち = 角速度たち [シャッフルindices]
色たち = 色たち [シャッフルindices]
plt.subplot(1, 2, 2)
plt.scatter(ステップたち, 角速度たち, color=色たち, alpha=0.5, s=0.25)
# plt.gca().axhline(0, color='k', alpha=0.5, zorder=-1) # 角速度0の線を引きたければコメント解除
plt.xlim(ステップ数 - 2189, ステップ数)
plt.ylim(-180, 180)
plt.xlabel("step")
plt.ylabel("angular velocity [deg]")
plt.ticklabel_format(style='plain',axis="x")
plt.tight_layout()
plt.savefig("angvel.png")
plt.close("all")
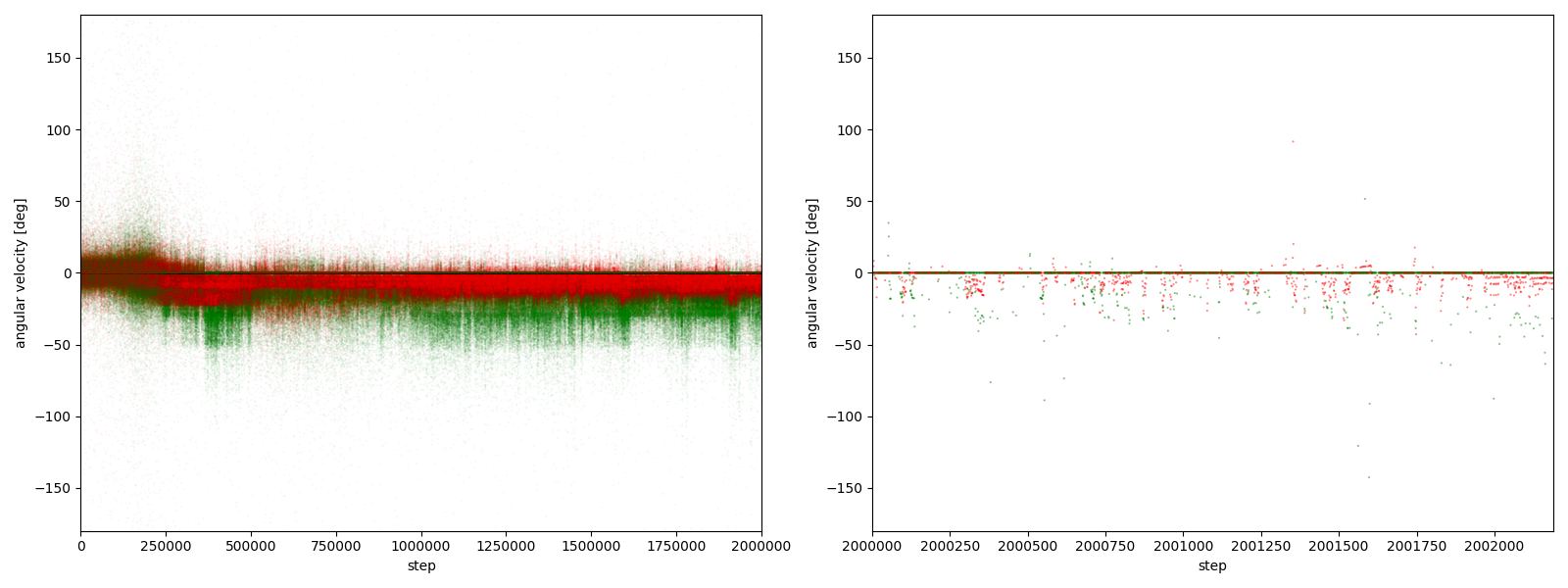
すると、図3-7-1~図3-7-10のようなグラフが得られた。(赤がグー、緑がチョキ。正方向が反時計回り)
図3-7-1~図3-7-10(赤がグー、緑がチョキ。正方向が反時計回り)
実験5-1
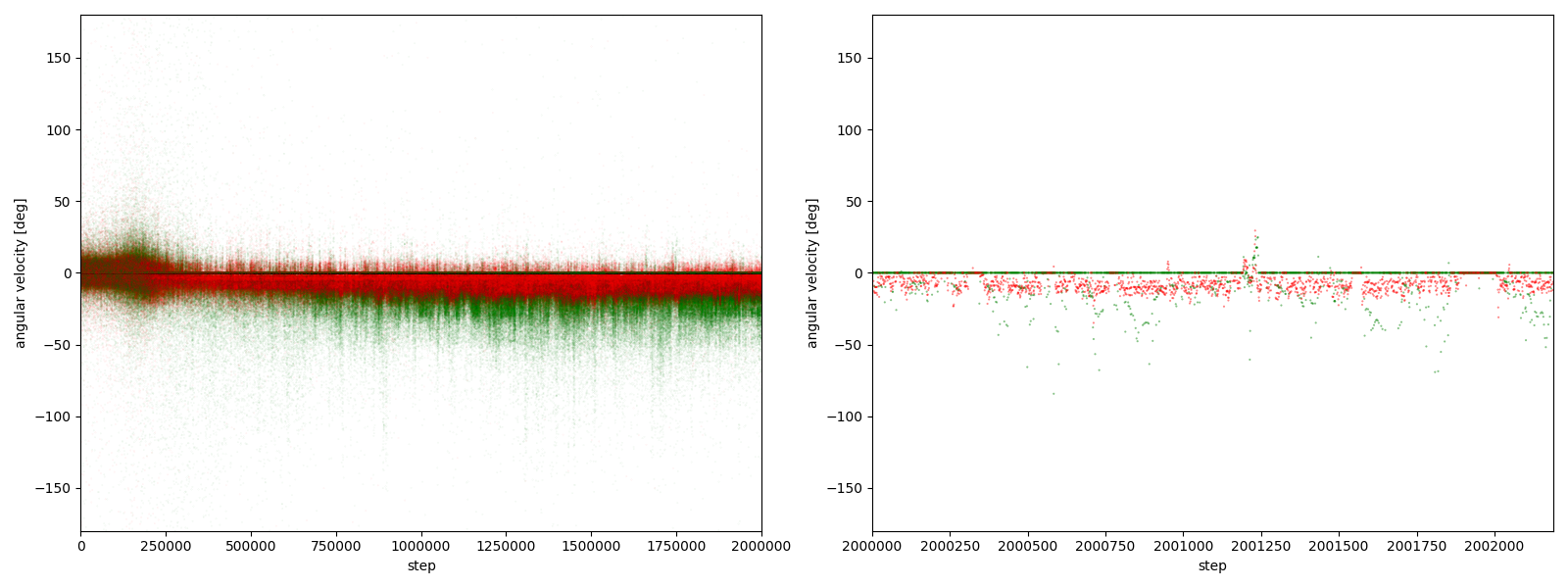
図3-7-1. 実験5-1における、パーに対するグーやチョキの角速度
実験5-2
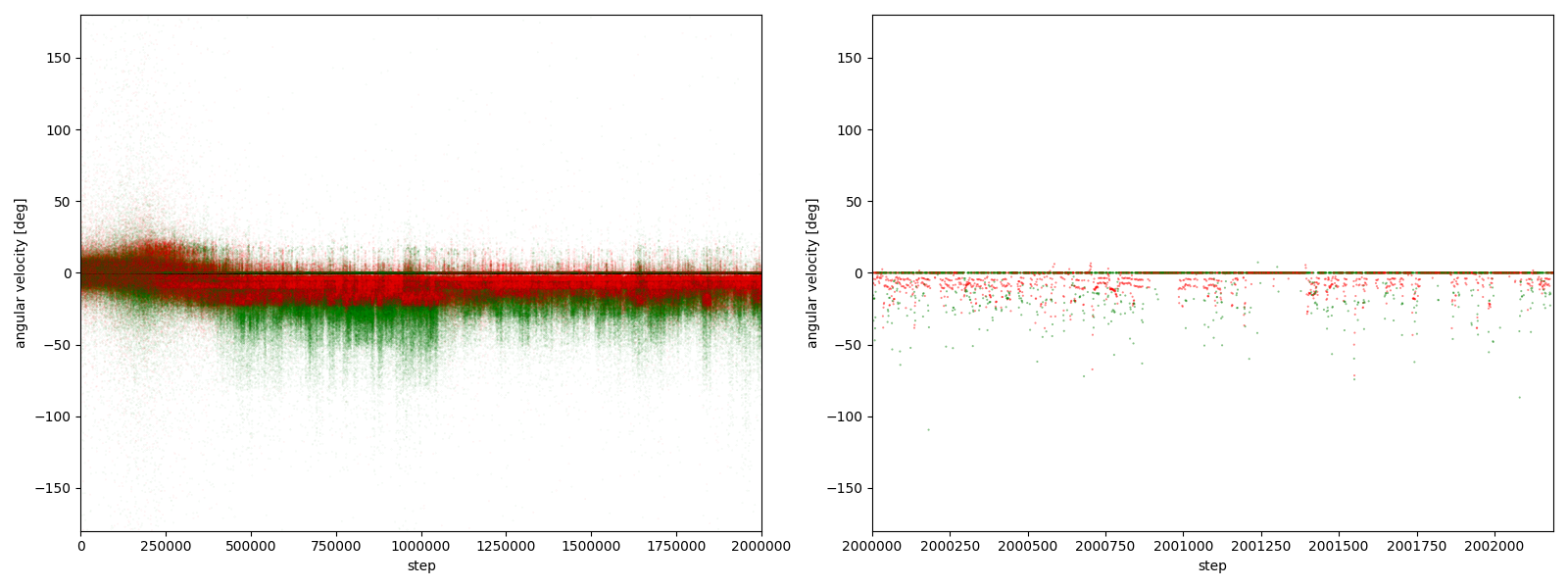
図3-7-2. 実験5-2における、パーに対するグーやチョキの角速度
実験5-3
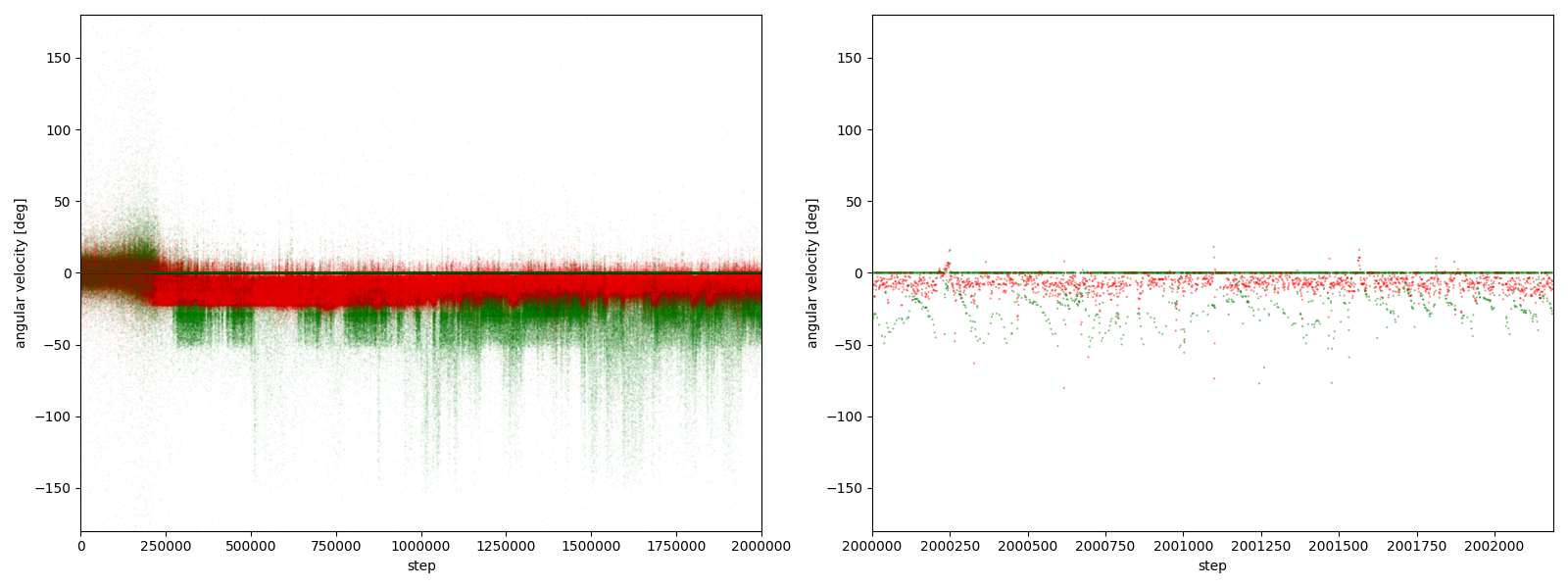
図3-7-3. 実験5-3における、パーに対するグーやチョキの角速度
実験5-4
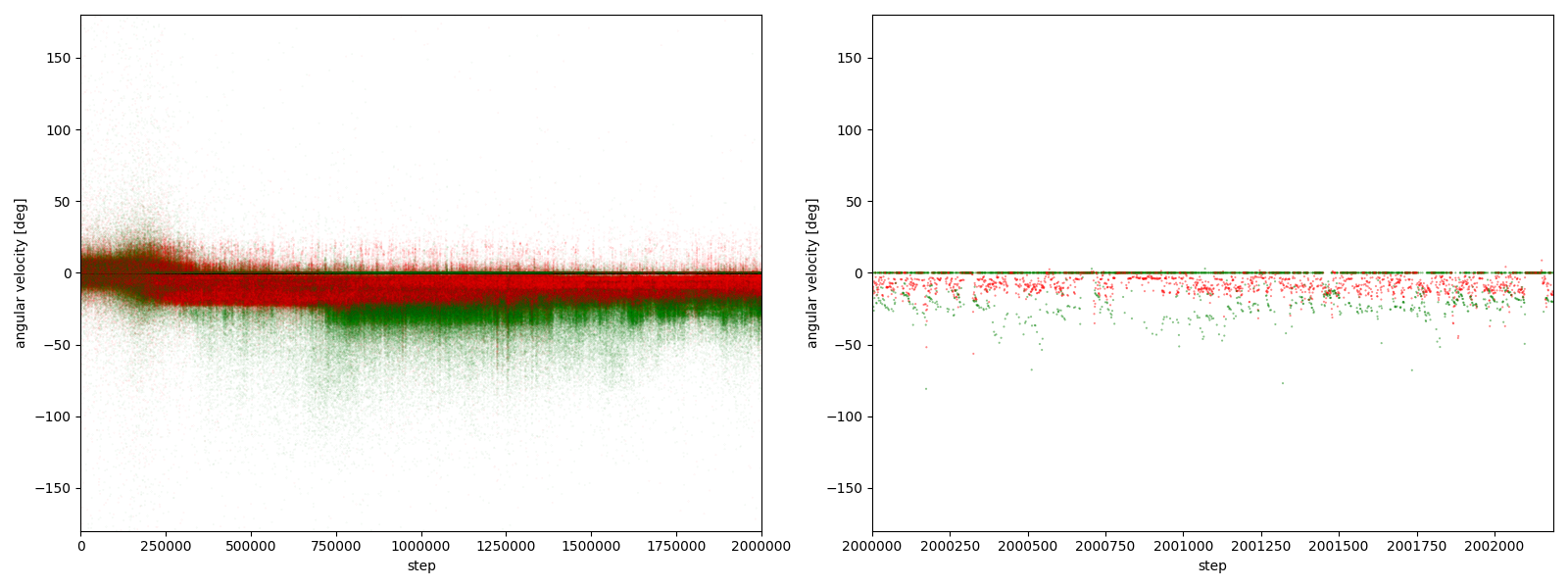
図3-7-4. 実験5-4における、パーに対するグーやチョキの角速度
実験5-5
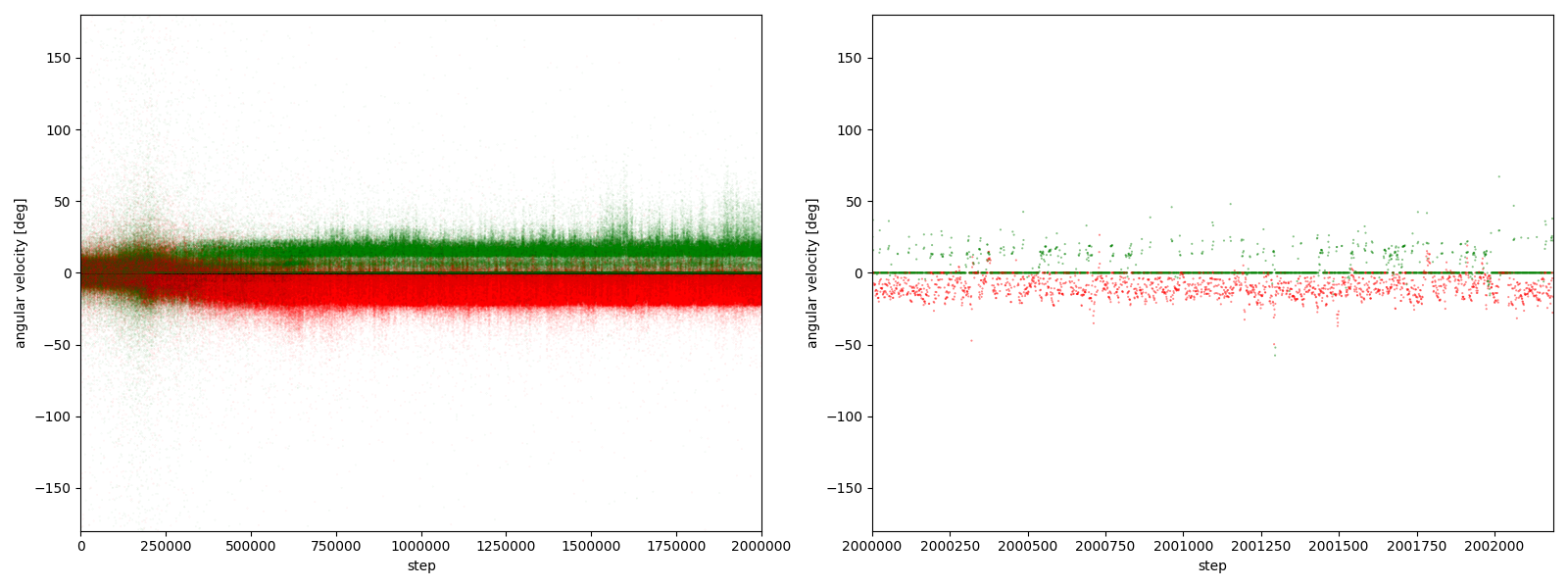
図3-7-5. 実験5-5における、パーに対するグーやチョキの角速度
実験5-6
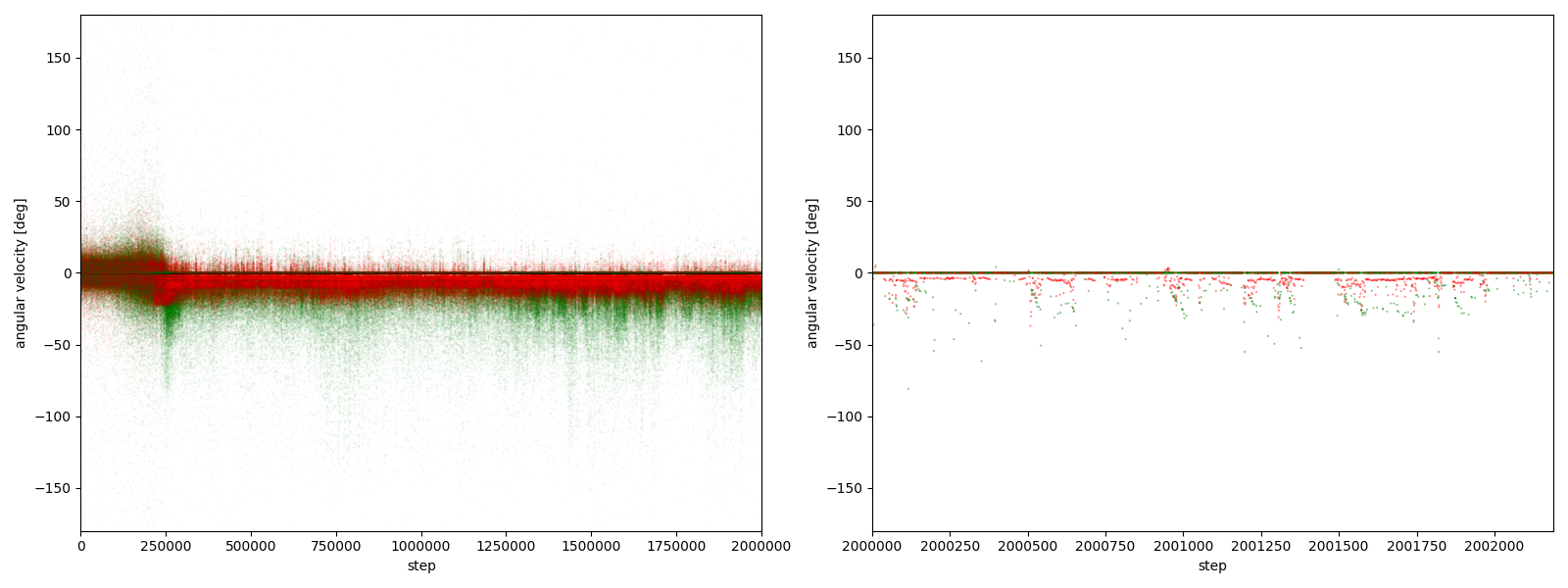
図3-7-6. 実験5-6における、パーに対するグーやチョキの角速度
実験5-7
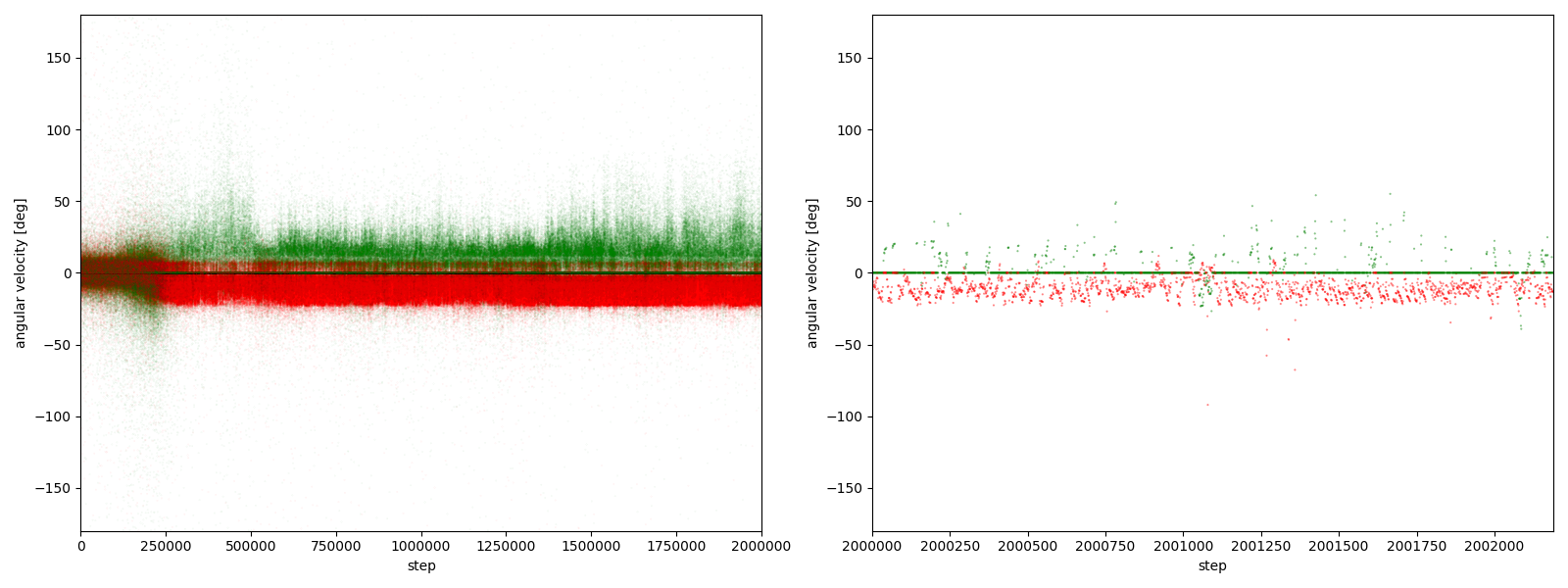
図3-7-7. 実験5-7における、パーに対するグーやチョキの角速度
実験5-8
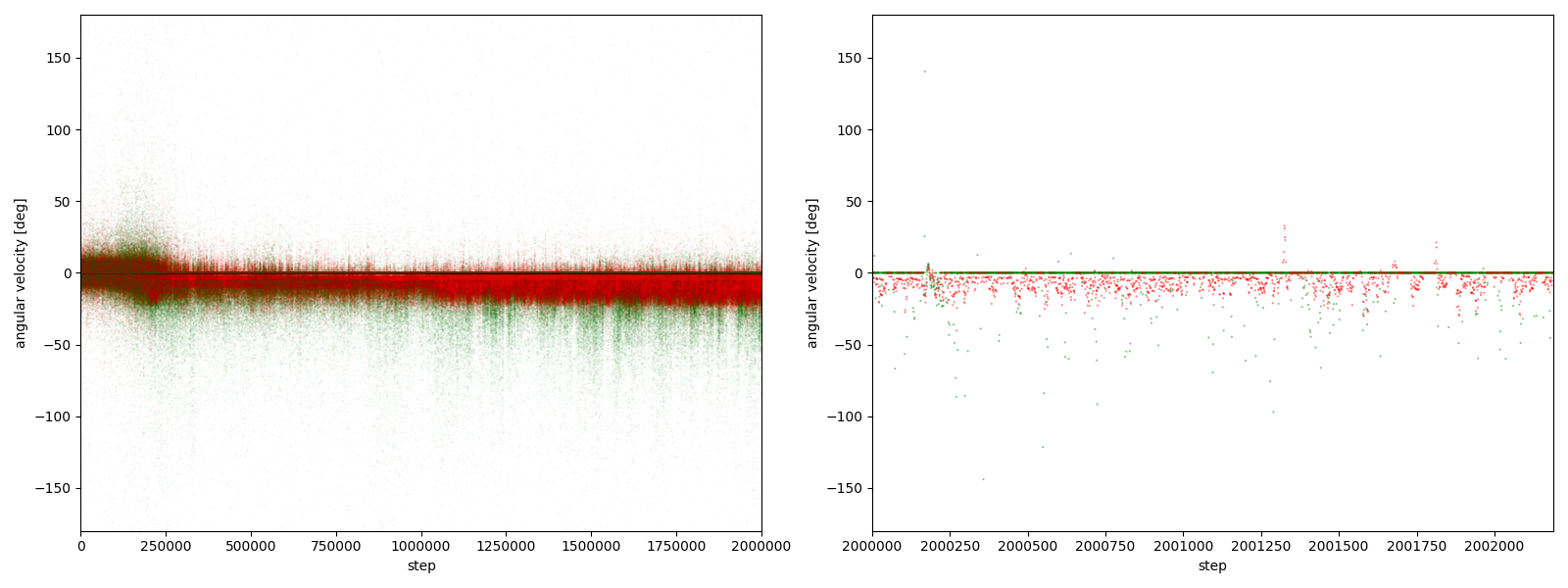
図3-7-8. 実験5-8における、パーに対するグーやチョキの角速度
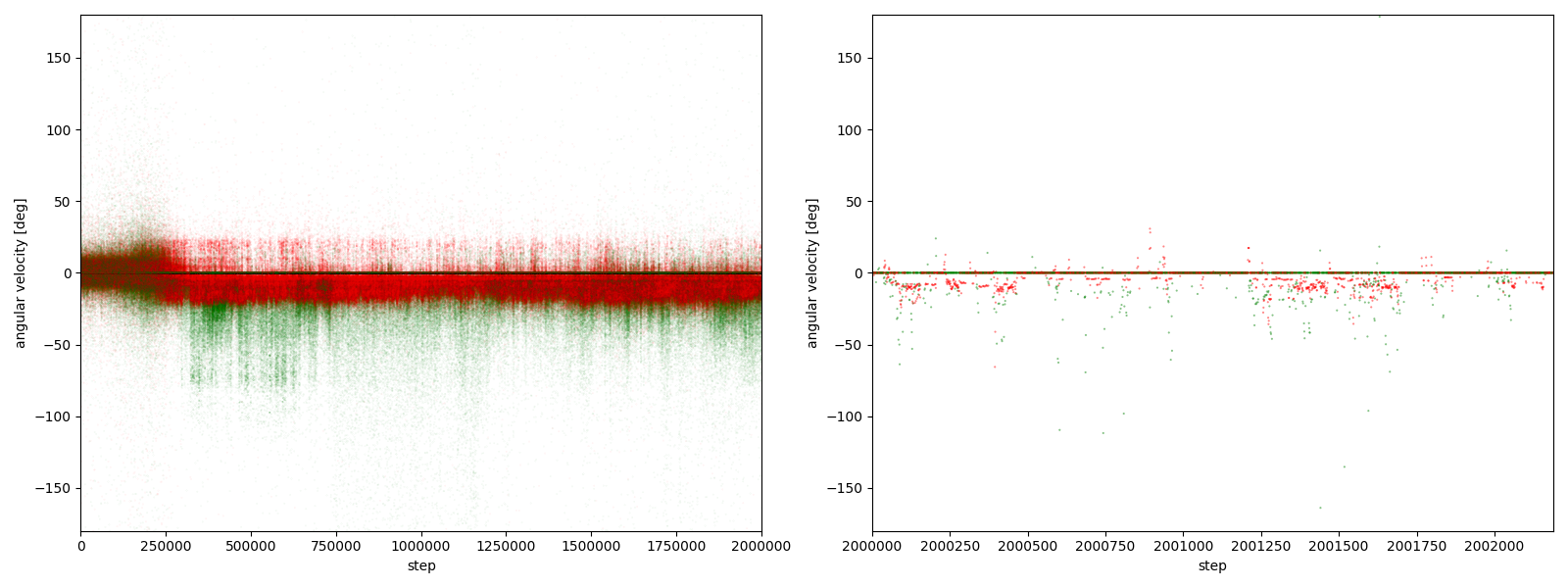
図3-7-1~図3-7-10 から、$2000000$ステップ目以降、10回の再実験のうち、
- 10回すべてにおいて、グーの角速度はほとんど $-25~0^\circ$、つまり時計回りである
- 10回すべてにおいて、チョキの角速度は基本的に $0$ (静止)である
- 8回において、チョキの角速度がしばしば $-50~0^\circ$、つまり時計回りになる
- 2回において、チョキの角速度がしばしば $0~50^\circ$、つまり反時計回りになる
ことが分かる。
チョキが反時計回りになる例として、実験5-5があるので、その $2000000~2000499$ステップを表示したGIFアニメが、図3-7-11である。
図3-7-11. 実験5-5 でチョキが反時計回りに逃げるGIFアニメ
3-7-2. 考察1. 反時計回りに動く場合があるチョキについて
図3-7-11 を見る限り、チョキが反時計回りに動く結果が得られた実験においては、
チョキは「グーの反対方向に動くことで、グーに捕まる時間を短くする」という戦略をとっているように見える。
下手にグーから必死に逃げて、パーに触れる機会を減らすくらいなら、
常にパーに触れて大きな報酬を獲得し続けつつ、一瞬だけグーに触れて負の報酬を受け取る戦略のほうが、
長期的に見て価値が高いというわけだ。
3-7-3. 考察2. 時計回りを好むグーについて―Q値を見てみる
また、なぜグーが時計回りに偏り、反時計回りをほとんどしないのかを探るべく、
グーの $2000000$ステップ目におけるQ値の平均値を、
獲物の向きと方向の変化毎にまとめたものが 図3-7-12 である。
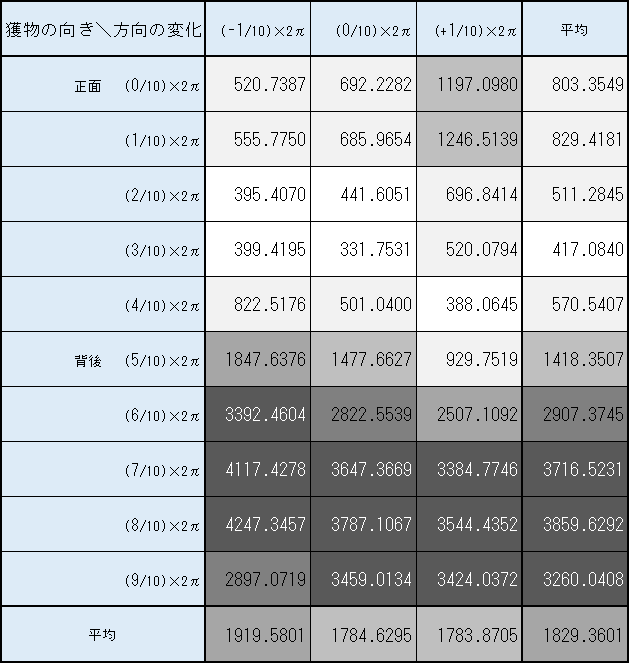
図3-7-12. 実験5-5 グーの $2000000$ステップ目における獲物の向きと方向の変化毎のQ値の平均値
図3-7-12 を見ると、
- 「獲物の向き」ごとの「方向の変化」の平均(一番右の列) から、獲物(チョキ)が正面右 ($((7~9)/10)\times2\pi$) にいるときにQ値が顕著に高いことが分かる。
- 「方向の変化」ごとの「獲物の向き」の平均(一番下の行) から、時計回り ($(-1/10)\times2\pi$) の行動のQ値が若干高いことが分かる。
このことから、グーはやはり時計回りの行動をどちらかといえば選んでいることが分かり、
またチョキが正面右向きにいるときに、チョキを捕まえやすい傾向が顕著にあることがわかる。
つまり、獲物であるチョキを正面右向きに見るときに大きなQ値となるので、
まず、グーはチョキを正面右向きにみようとする。
そして、正面右向きにいる獲物を捕らえるために、時計回りの行動をとるものと説明できる。
しかし、ではなぜ「正面右向き」に獲物がいるときにQ値が大きくなるという偏った傾向が生まれるのだろうかという疑問が残る。
対称性を考えれば、「正面右向き」の価値と「正面左向き」の価値は本来同程度であるはずだ。
3-7-4. 考察3. 時計回りを好むグーについて―Q値の偏りの原因を探る
獲物が「正面右向き」にいるときのQ値が大きくなり、「正面左向き」の場合はそうでないという、Q値の対称性の崩れた傾向が生まれる原因を探るため、図3-7-13のように、図3-7-12を環状にして獲物の向き$0$と$2\pi$を接続したレーダーチャート、およびその中央差分のレーダーチャートを作った。
すると、$0$と$2\pi$($0^\circ$と$360^\circ$)の間でQ値の平均値に大きな変化があることがわかった。
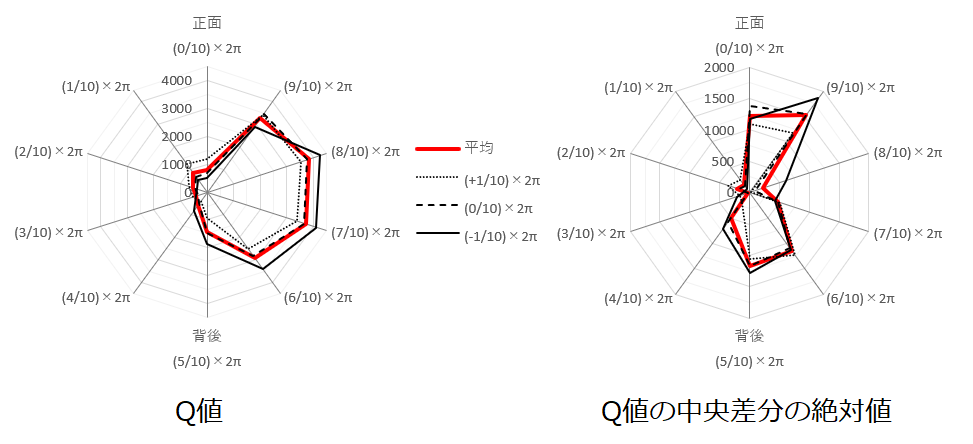
図3-7-13. 実験5-5 グーの $2000000$ステップ目における獲物の向きと方向の変化毎のQ値の平均値のレーダーチャート
その理由として、獲物の向きを離散化する際に、「均等に」離散化されていないことが挙げられる。
連続値としての獲物の向きは、 最も近いものを選ぶ 関数により、 向きリスト 内の離散値に近似される。
この近似は $0$や$2\pi$ の付近で、不均等に離散化される。これは、表3-7-1に示す、離散化される連続値の範囲を確認することで明らかになる。
表3-7-1. 離散値に対応する角度の範囲
| 離散値 | 範囲最小値 | 範囲最大値 | 範囲の大きさ |
|---|---|---|---|
| $(0/10)\times 2\pi$ | $(0/10)\times 2\pi$ | $(0.5/10)\times 2\pi$ | $(0.5/10)\times 2\pi$ |
| $(1/10)\times 2\pi$ | $(0.5/10)\times 2\pi$ | $(1.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(2/10)\times 2\pi$ | $(1.5/10)\times 2\pi$ | $(2.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(3/10)\times 2\pi$ | $(2.5/10)\times 2\pi$ | $(3.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(4/10)\times 2\pi$ | $(3.5/10)\times 2\pi$ | $(4.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(5/10)\times 2\pi$ | $(4.5/10)\times 2\pi$ | $(5.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(6/10)\times 2\pi$ | $(5.5/10)\times 2\pi$ | $(6.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(7/10)\times 2\pi$ | $(6.5/10)\times 2\pi$ | $(7.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(8/10)\times 2\pi$ | $(7.5/10)\times 2\pi$ | $(8.5/10)\times 2\pi$ | $(1/10)\times 2\pi$ |
| $(9/10)\times 2\pi$ | $(8.5/10)\times 2\pi$ | $(10/10)\times 2\pi$ | $(1.5/10)\times 2\pi$ |
表3-7-1から、離散値 $(0/10)\times 2\pi$ のみ、対応する連続値の範囲が他の離散値 ($((1~8)/10)\times 2\pi$) の半分と狭く、
また離散値 $(9/10)\times 2\pi$ のみ、対応する連続値の範囲が他の離散値の$1.5$倍大きく、
それ以外の離散値でのみ範囲の大きさが均等であることが分かる。
よって、獲物の向きが離散値 $(9/10)\times 2\pi$ (正面右向き)のときの学習機会が、
$(1/10)\times 2\pi$ (正面左向き)のときの学習機会と比較して1.5倍もあることになる。
これが「正面右向き」と「正面左向き」の対称性を崩し、「正面右向き」のQ値が不自然に大きくなる原因であると考えられる。
3-7-5. 考察4. グーを時計回りに偏らなくするためには
前述した、離散値に対応する連続値の範囲の不均等を解消することで、
対称性が保たれるようになり、グーの挙動が時計回りあるいは反時計回りのどちらかに偏らないようになるはずである。
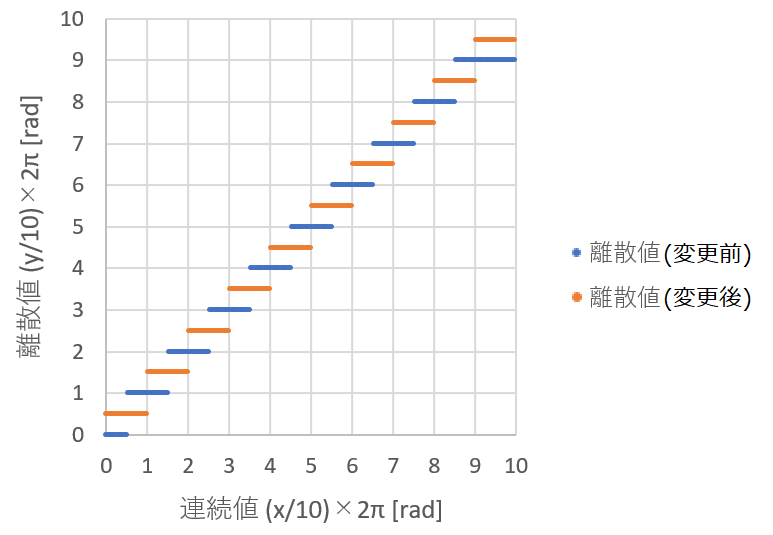
そのためには、向きの離散値を
$(0/10)\times 2\pi$, $(1/10)\times 2\pi$, ..., $(9/10)\times 2\pi$
から
$(0.5/10)\times 2\pi$, $(1.5/10)\times 2\pi$, ..., $(9.5/10)\times 2\pi$
に変更すればよい。
すると、図3-7-14のように、離散値に対応する連続値の範囲の大きさが均等になり、
正面左向きと正面右向きの対称性が保たれるようになる。
3-8. 実験6
実験5では、向きの離散化の方法が不適切であった故、向きの対称性が崩れ、「獲物を時計回りに追いかけやすく、反時計回りに追いかけにくい」という傾向が生まれたことを突き止めた。
そこで実験6では向きの離散化の方法を適切にし、向きの対称性を保ち、時計回りの起こりやすさと反時計回りの起こりやすさを等しくした上で、実験5と同じ実験を10回繰り返しながら、グーとチョキのパーに対する角速度をプロットしてみることにした。
3-8-1. 実験6のコードと実行
具体的には ./実験5.py のハイパーパラメータ、状態と行動のリストを次のように変更した ./実験6.py を実行してみた。
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 0
目標速さ = 4
環境の幅 = 75
環境の高さ = 75
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [(i+0.5) * (2 * np.pi / 10) for i in range(10)] # 実験5からの変更点
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), 0, (2 * np.pi / 10)]
速さの変化リスト = [-2, -1, 0, 1, 2]
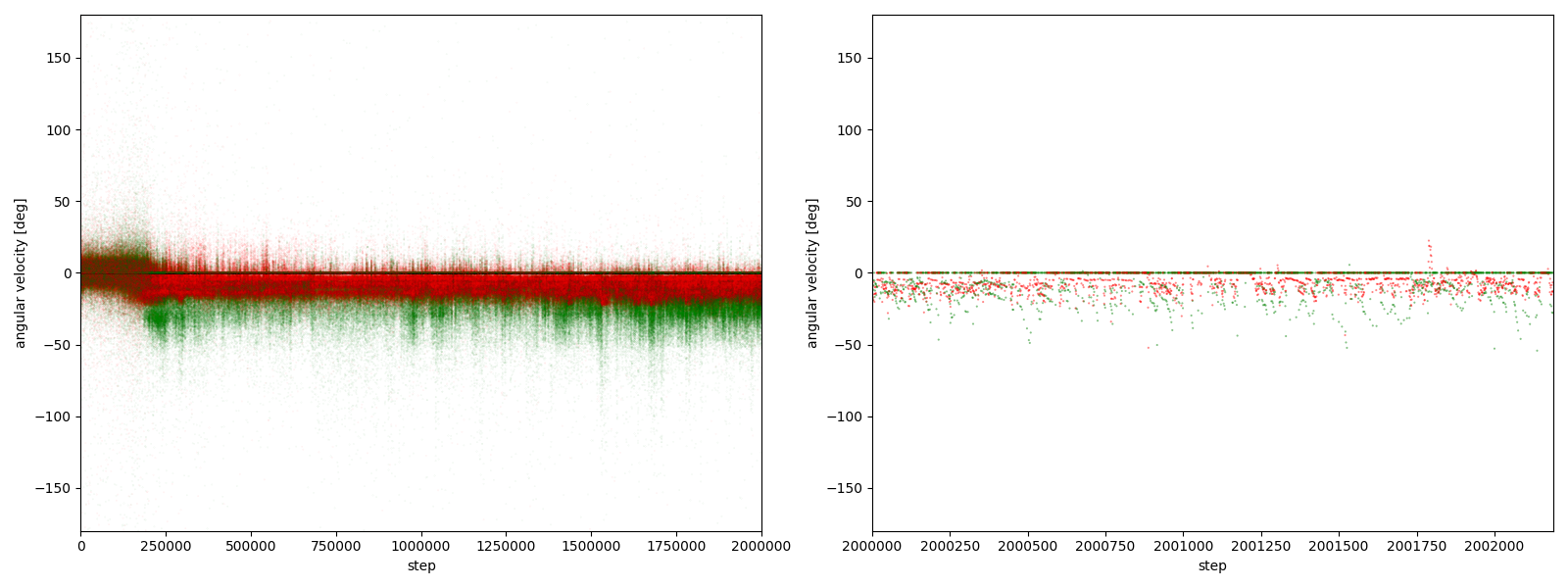
すると、図3-8-1~図3-8-10のようなグラフが得られた。(赤がグー、緑がチョキ。正方向が反時計回り)
図3-8-1~図3-8-10(赤がグー、緑がチョキ。正方向が反時計回り)
実験6-1
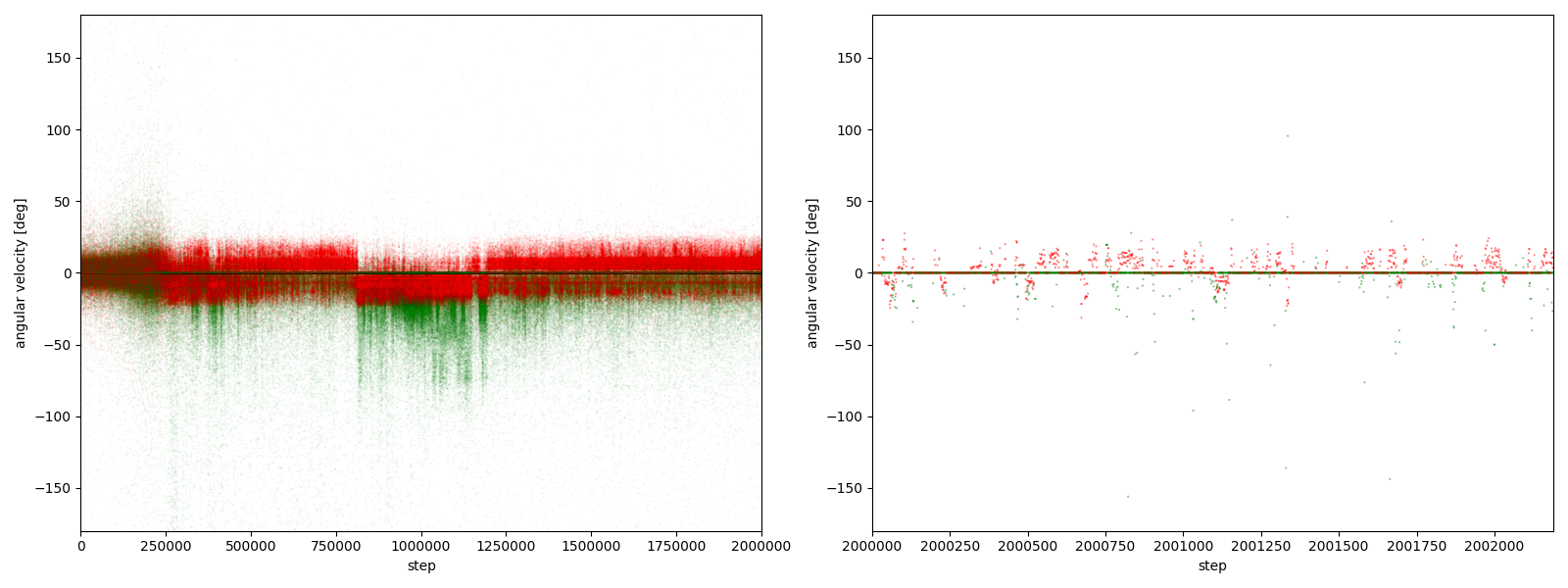
図3-8-1. 実験6-1における、パーに対するグーやチョキの角速度
実験6-2
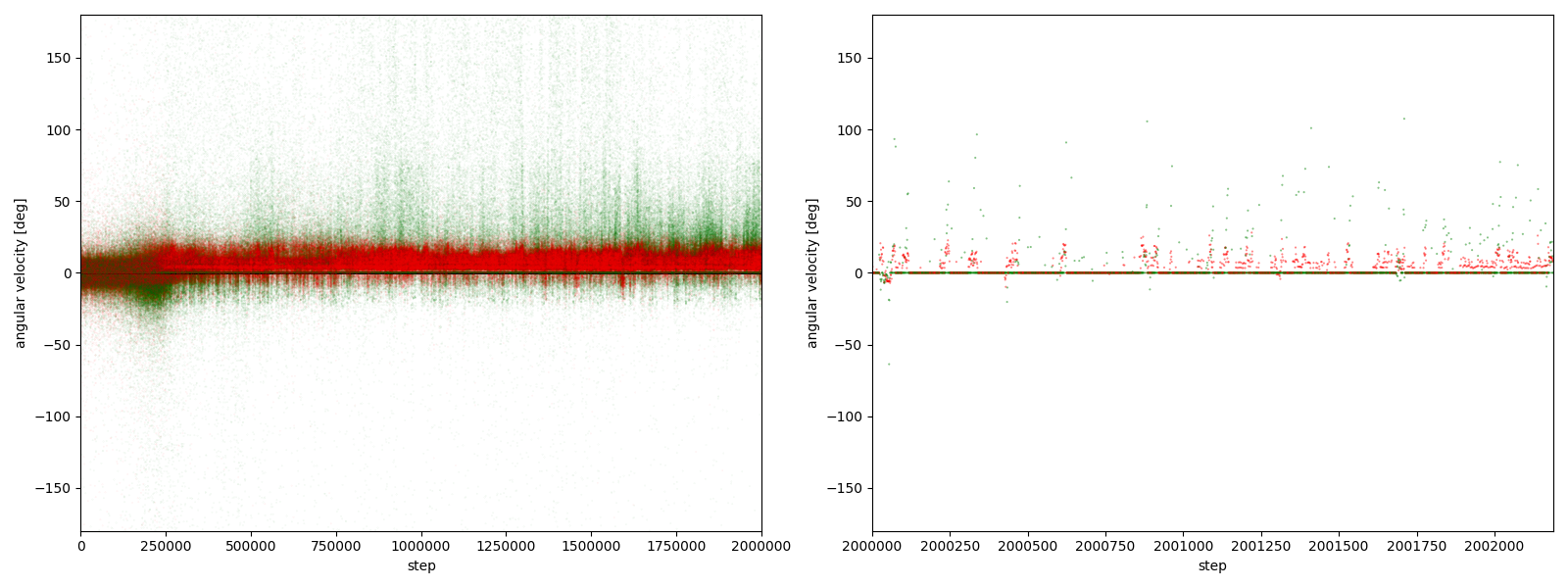
図3-8-2. 実験6-2における、パーに対するグーやチョキの角速度
実験6-3

図3-8-3. 実験6-3における、パーに対するグーやチョキの角速度
実験6-4
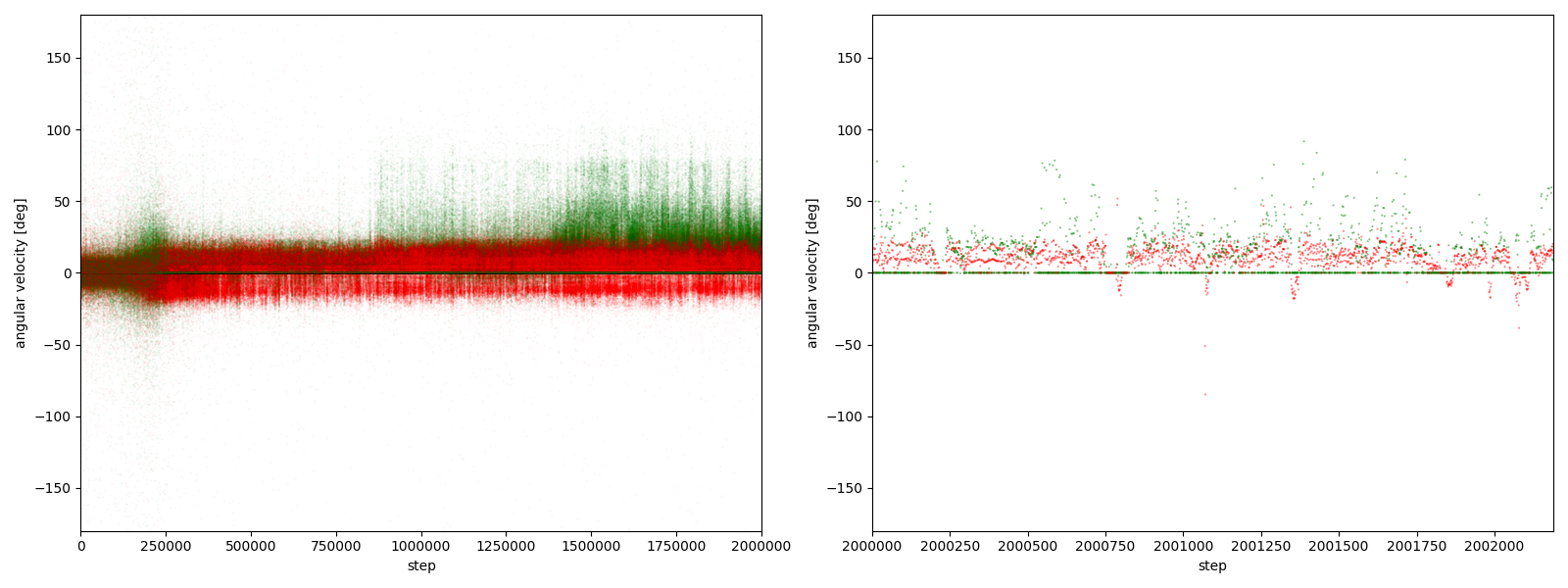
図3-8-4. 実験6-4における、パーに対するグーやチョキの角速度
実験6-5
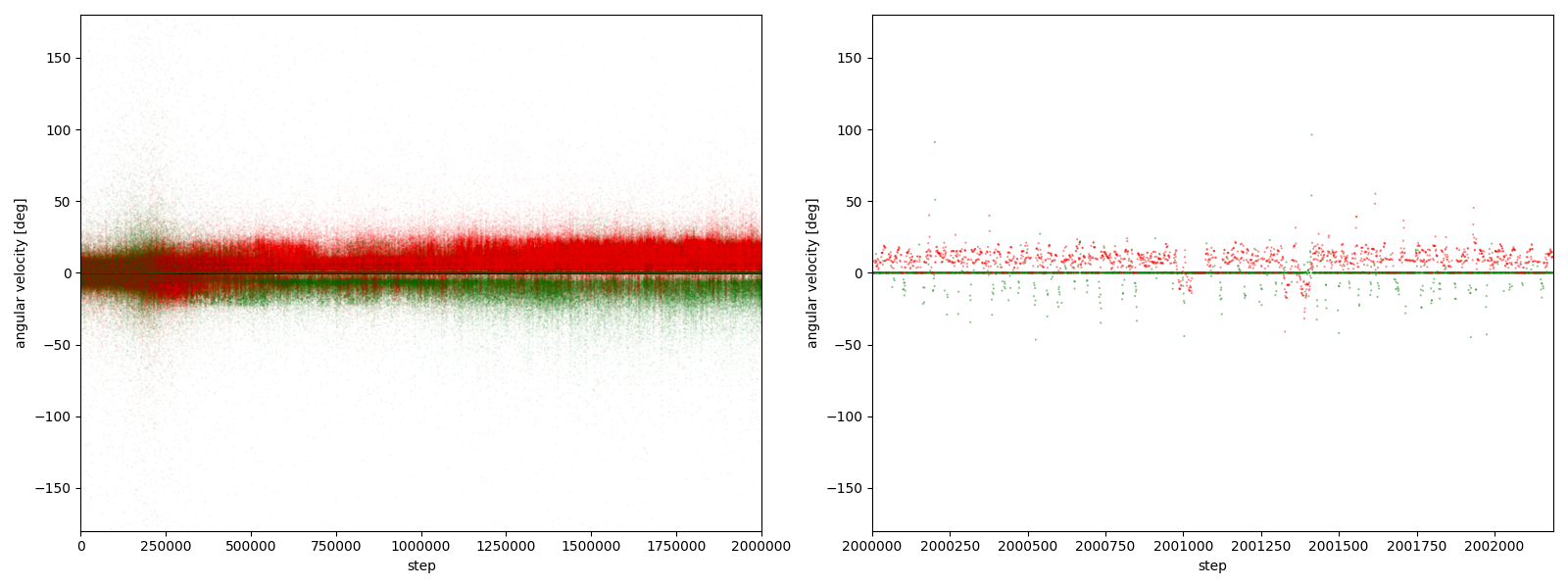
図3-8-5. 実験6-5における、パーに対するグーやチョキの角速度
実験6-6
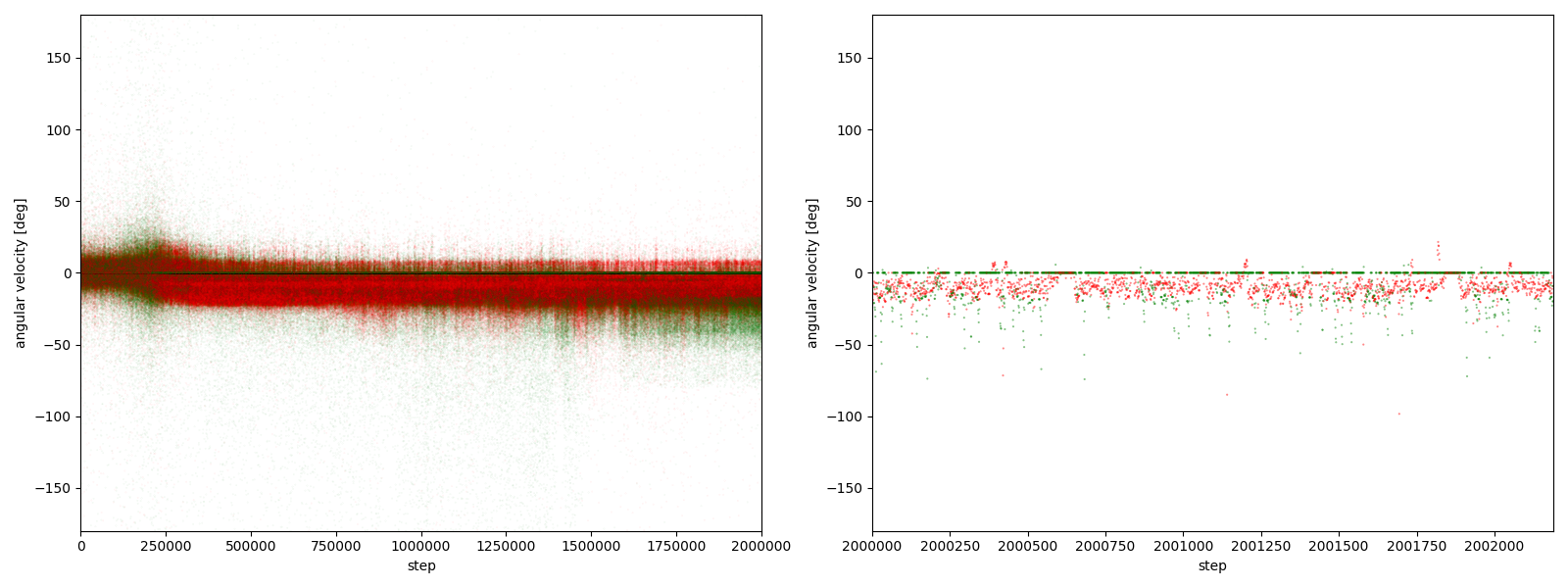
図3-8-6. 実験6-6における、パーに対するグーやチョキの角速度
実験6-7
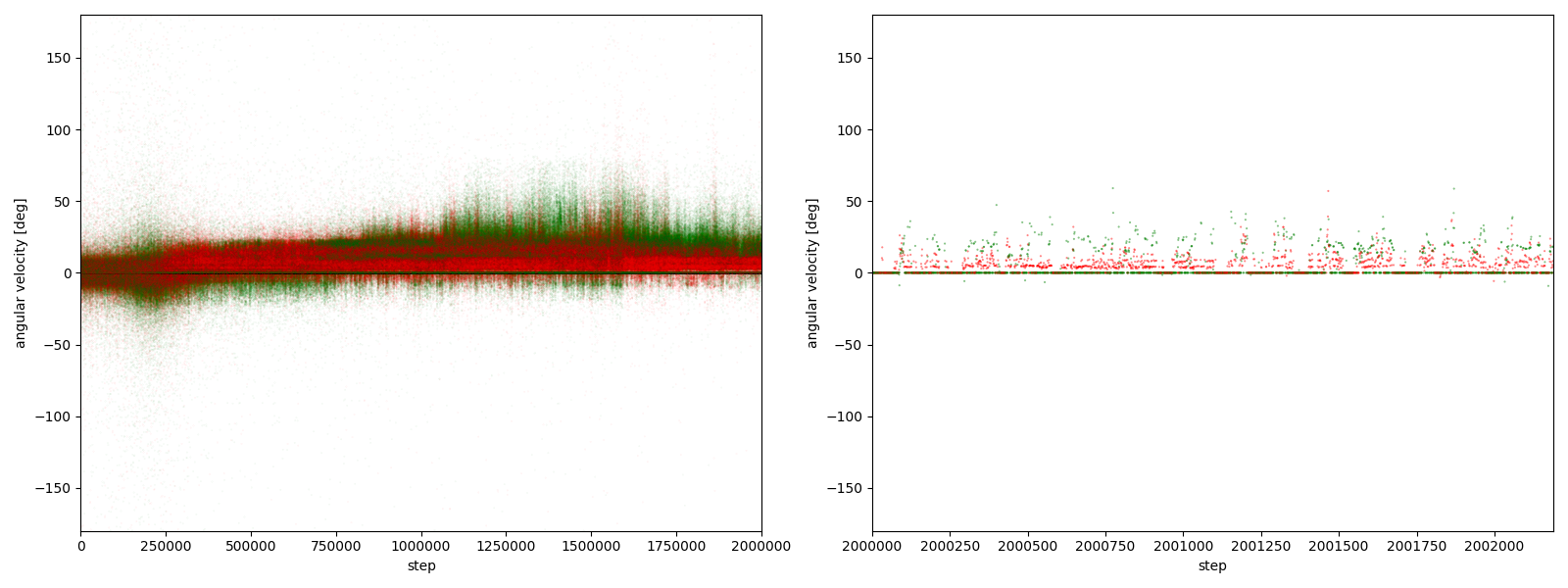
図3-8-7. 実験6-7における、パーに対するグーやチョキの角速度
実験6-8
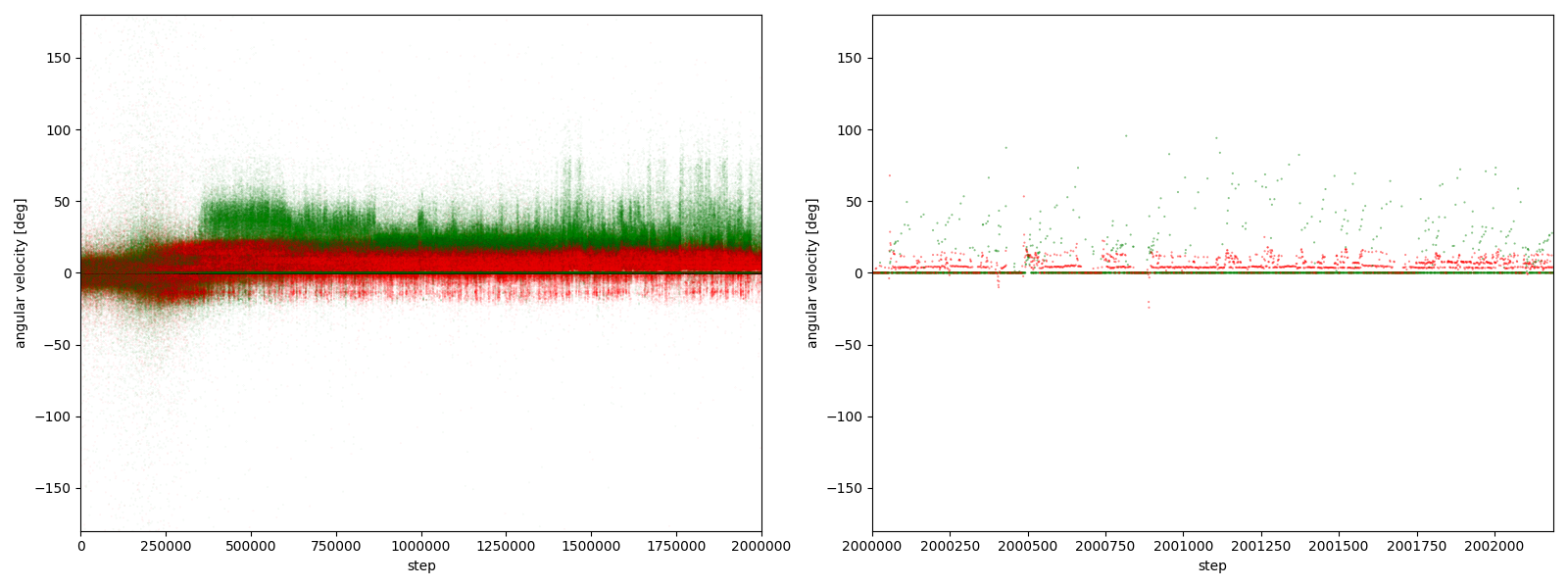
図3-8-8. 実験6-8における、パーに対するグーやチョキの角速度
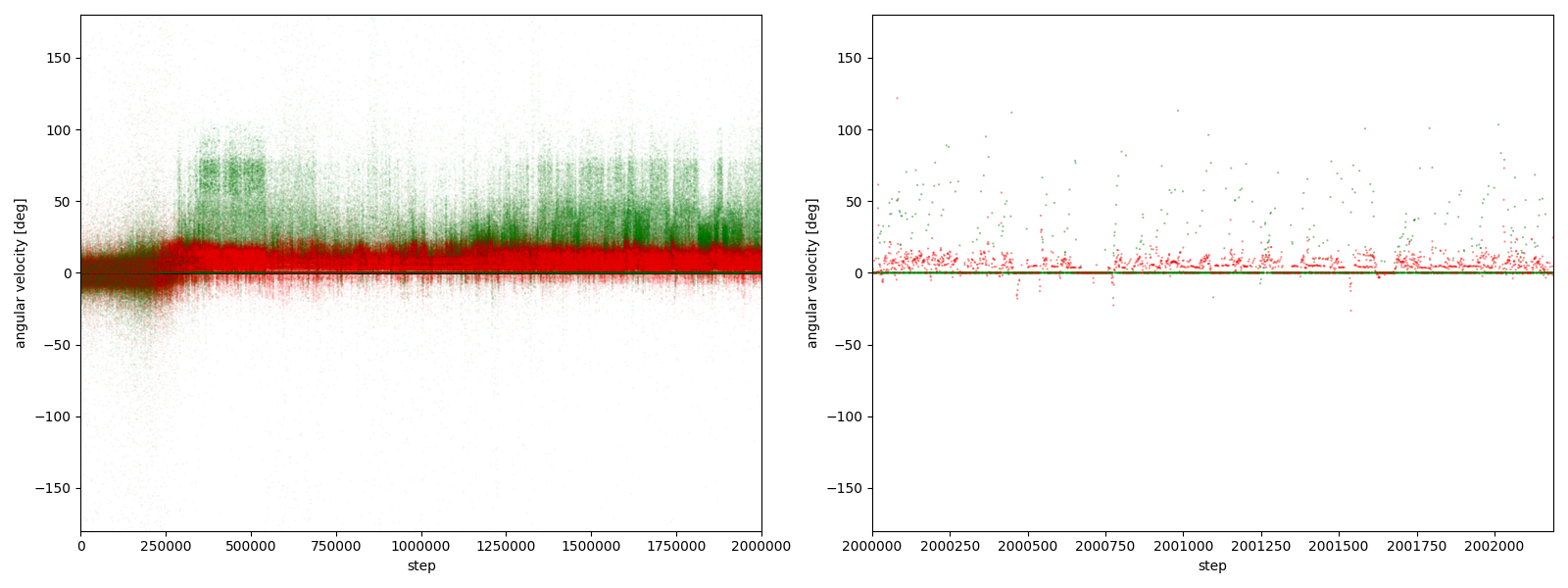
図3-8-1~図3-8-10 から、$2000000$ステップ目以降、10回の再実験のうち、
- 9回において、グーは反時計回りまたは時計回りのどちらかに偏っている
- 7回において、グーはほとんど反時計回りをしている
- 2回において、グーはほとんど時計回りをしている (実験6-6, 6-9)
- 1回において、グーは反時計回りをしたり時計回りをしたりしている (実験6-1)
ことが分かる。
3-8-1. 考察1 ε-greedy法と対称性の破れ
ほとんどの実験で、グーは反時計回りまたは時計回りのどちらかに偏っていたが、実験5と違い、反時計回りだけ、あるいは時計回りだけに偏ることはなく、反時計回りにも時計回りにも、場合によってどちらにも偏っていた。
このこと自体は、$\varepsilon$-greedy法という学習の仕組み上自然であると考えられる。
なぜなら、確率$1-\varepsilon$ において、行動はQ値が最大になるものを決定論的に選ばれるためである。
例えば、次の場合を考えよう。
$1 - \varepsilon = 0.9$,
反時計回りの行動により更新される価値: 常に $+100$,
時計回りの行動により更新される価値: 常に $+100$,
現在のQテーブル = {反時計回り: $49.9$, 時計回り: $50.1$}
(状態は1通りに固定し、行動は「反時計回り」と「時計回り」のみと仮定)
現在のQテーブルに置いて、反時計回りの行動と時計回りの行動の価値は、ノイズ程度の差しかなく、ほぼ対称的である。
しかしながら、次に選ばれる行動は、確率 $0.9 + (0.1/2)=0.95$ で最大Q値である時計回りである。
そして報酬 $100$ を受け取り、次ステップのQテーブルは
{反時計回り: $49.9$, 時計回り: $150.1$}
となる。
一方、反時計回りの行動が選ばれ、次ステップのQテーブルが
{反時計回り: $149.9$, 時計回り: $50.1$}
となる確率は わずか $0.1/2 = 0.05$ である。
次ステップのQテーブルの期待値を求めると、
{反時計回り: $0.05 \times 149.9 + 0.95 \times 49.9$, 時計回り: $0.95 \times 150.1 + 0.05 \times 50.1$}
= {反時計回り: $54.9$, 時計回り: $145.1$}
となり、対称性が破れ、時計回りのQ値が有意に大きくなる。
このようにして、「Q値が最大になる行動」を決定論的に選ぶことにより、
行動の対称性が自発的に破れることが、自然と考えられるのである。
3-8-2. 考察2
また、グーが反時計回りにも時計回りにも行動していた実験6-1の $2000000~2000499$ステップを表示したGIFアニメが、図3-8-11である。
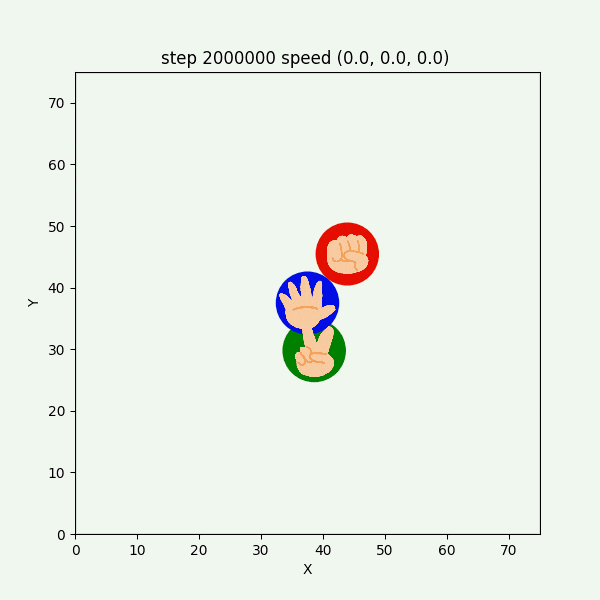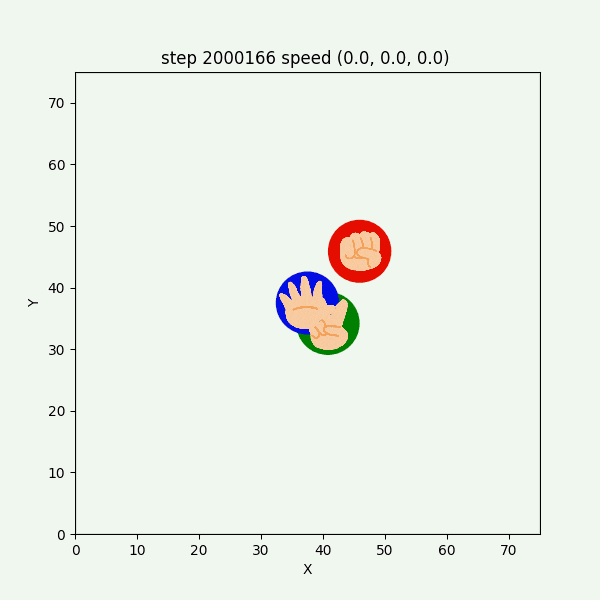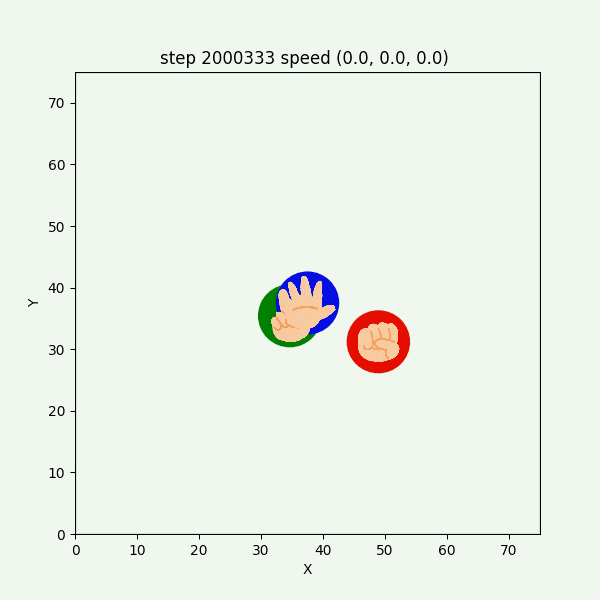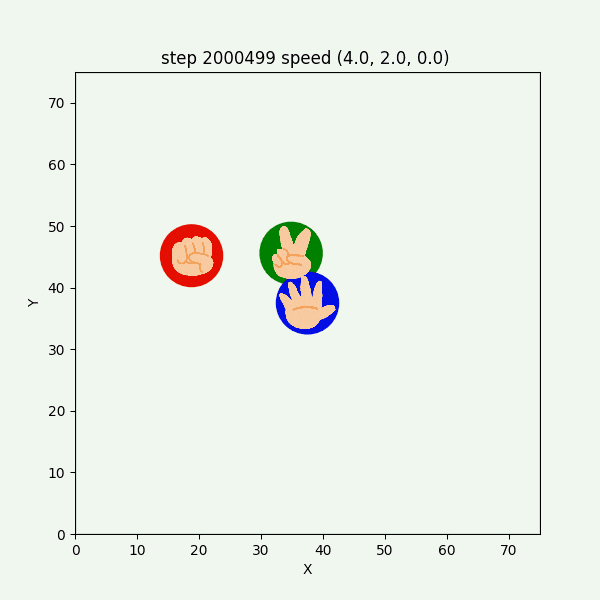
図3-8-11. 実験6-1 でグーが反時計回りにも時計回りにも動くGIFアニメ
グーもチョキも基本的に静止していて、突然グーが動き出す挙動をしていた。
3-9. 実験7
実験7では、実験6とほぼ同じ条件で、パーの固定を解除したらどのような挙動をするか観測してみる。
具体的には、 ./base.py のハイパーパラメータ、状態と行動のリストを次のように変更した ./実験7.py を実行してみた。
# ハイパーパラメータ
学習率 = 0.3
割引残率 = 0.999
探索率 = 0.1
捕食報酬 = 1000
速さ報酬係数 = 0
目標速さ = 4
環境の幅 = 75
環境の高さ = 75
# 状態と行動のリスト
距離リスト = [5, 15, 20, 25, 30, 35, 40, 45, 50, 75, 100]
向きリスト = [(i+0.5) * (2 * np.pi / 10) for i in range(10)]
速さリスト = [0, 1, 2, 3, 4]
方向の変化リスト = [-(2 * np.pi / 10), 0, (2 * np.pi / 10)]
速さの変化リスト = [-2, -1, 0, 1, 2]
すると、次のような結果となった。
動画3-9-1. 実験7の結果
$400000$ステップ目以降から、チョキがパーを追い、パーがチョキから逃げながらグーを追うが、
グーはパーから逃げるだけでチョキをあまり積極的に追わない傾向がみられた。
但し、それだけだとグーは報酬を貰えないので、グーは時々立ち止まり、パーに敢えて一瞬捕まった直後、チョキをネズミ捕り式に捕まえて報酬を得ることをしていた。
(図3-9-2)

図3-9-2. パーから逃げつつ、時々敢えてパーに捕まってその直後チョキをネズミ捕りするグーのGIFアニメ
これは、対称的な関係であるはずのグー・チョキ・パーが、それぞれ異なる戦略を学習したことを意味する。
このことは、3-8-1節 実験6の「考察1 ε-greedy法と対称性の破れ」で述べた通り、ε-greedy法に従った方策を取ることで自然に発生する対称性の破れであると考えられる。
4. まとめ
強化学習について、実践を通じて理解を深めることが出来た。
特に、
- 実験4で、環境の広さと学習の様子の関係を確認することが出来た。
- 実験6で状態(や行動)の離散化方法の誤りが、実験結果の偏りに与える影響や、
ε-greedy法がもたらす対称性の破れについて、実際に観測し、かつ理論的に考察できた。
-
https://www.brainpad.co.jp/doors/contents/01_tech_2017-02-24-121500/ ↩
-
強化学習では、時刻、つまり機械(エージェント)と環境の相互作用が行われるタイミングのことを「ステップ」という。
また、ゲーム、あるいはゲームの開始から終了までのことを「エピソード」という。また機械のことを「エージェント」という。 ↩ ↩2 -
本当に囲碁を機械に学習させる場合、強化学習だけでは状態数が多すぎて手に負えない。そこで、「深層強化学習」という手法を使う場合が多い。この記事では詳解しない。 ↩
-
「各ステップに報酬が貰えない」からモンテカルロ法を使っているのに、なぜモンテカルロ法の更新式に$r_{e,t}$ が出てくるのか?と疑問に思うかもしれない。実際その通りで、ほとんどの$e,t$において、 $r_{e,t}=0$ となる理解で問題ない。 ↩