More than 1 year has passed since last update.

【強化学習】第3回 - モンテカルロ(MC)法とTD(0)学習、TD(λ)学習について解説

Last updated at 2022-11-15Posted at 2022-11-07

はじめに

前回は遷移確率 $P$ や報酬 $R$ が既知の場合に状態価値関数を計算する方法について扱いました。しかし実際に強化学習を行う際は、むしろ遷移確率や報酬は未知である場合が多いです。第3回である本稿では、モデルが未知の場合に適用できるアルゴリズムとして「モンテカルロ法」と「TD(0)学習」「TD(λ)学習」の3つを紹介します。なお、強化学習にはSutton & Bartoによるバイブル的な参考書"Reinforcement Learning: An Introduction"があり、この記事もここに書かれている内容を元に作成しています。すべて英語ですが、参考にしてください。

前回 ▶ 【強化学習】第2回 - ベルマン方程式と方策反復法(PI)、価値反復法(VI)について解説
次回 ▶ 【強化学習】第4回 - SARSAとQ学習について解説

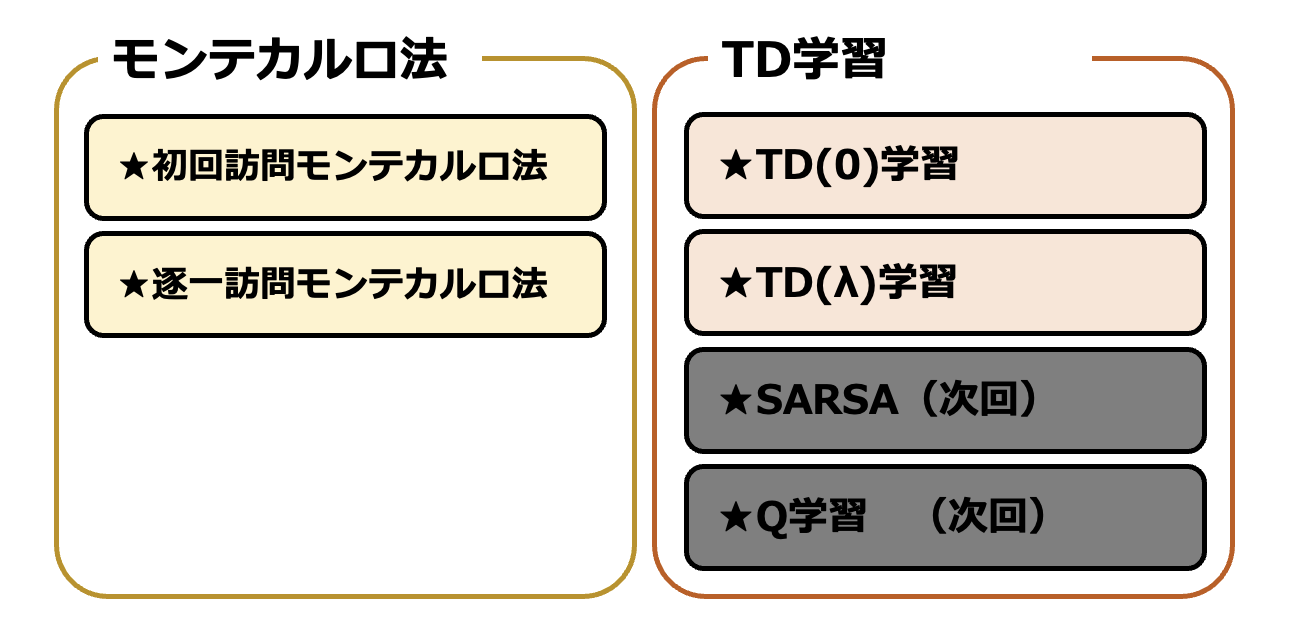
モデルフリーにおける方策評価

モデルフリーとは、モデルの情報を使用しないということです。すなわち、モデルフリーな学習は具体的な遷移確率 $P$ や報酬 $R$ が未知の際にも適用することができます。まずはモデルフリーな状況下における状態価値関数 $V^{\pi}(s)$ を評価する手法について見ていきましょう。モデルフリーな状況下において方策を改善する手法については第4回で扱います。

モンテカルロ法

第2回でも述べたように、最適な方策を求めるためには、方策の良さを知る必要があります。モデルの完全な情報が手元にない状態において、ある方策に従った際の各状態の将来的な報酬の見込み $V^{\pi}(s)$ を推測する方法について考えてみましょう。

具体的なモデルの情報が未知であっても、環境内で行動を重ねることでモデルの情報を推測することは可能です。モデルに従ったエピソードをいくつか用意した上で、それらのエピソードから得られる平均値を各状態の価値関数としましょう、というのがモンテカルロ法の発想です。Monte-Carloの頭文字を取ってMC法とも呼ばれます。

モンテカルロ法は、各状態がマルコフ的でない場合でも適用できます。一方でアルゴリズムの性質上、各エピソードのHorizon(長さ)は必ず有限である必要があります。本質的な差はありませんが、モンテカルロ法には初回訪問モンテカルロ法と逐一訪問モンテカルロ法の2種類があります。順に見ていきましょう。

初回訪問モンテカルロ法

モンテカルロ法という手法を用いて状態価値関数を評価する方法を説明します。ゴールは、方策 $\pi$ に従った行動の結果として得られた1つ以上のエピソードから、$\pi$ に従ったときの各状態における将来的な報酬の見込み $V^{\pi}(s)$ を推測することです。マルコフ決定過程のモデル $M$ において、$r_t$ を時刻 $t$ における報酬、$\gamma$を割引率とすると、時刻 $t$ からの将来的な報酬の見込み $G_t$ と状態価値関数 $V^{\pi}(s)$ はそれぞれ以下の式で定義されました。

$$
\begin{align}
&G_t=r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\cdots\\
&V^{\pi}(s)=\mathbb{E}[G_t\,|\,s_t=s]
\end{align}
$$

初回訪問モンテカルロ法における状態価値関数の評価は、以下の流れで行います。方策 $\pi$ に従った結果として得られたエピソード$i=s_{i,1},\,a_{i,1},\,r_{i,1},\,s_{i,2},\,a_{i,2},\,r_{i,2},\,\cdots,\,s_{i,n}$の集合を $I$ とします。

$\forall s\in S$ について $N(s)=0,\,G(s)=0$ と初期化する。
$\forall i\in I$ について、以下の処理を行う。
1. エピソード $i$ の中で訪問される任意の状態 $s$ について、以下の処理を行う。
  1. エピソード $i$ の中で初めて $s$ を訪問する時刻 $t$ を選ぶ。
  2. $G_{i,t}=r_{i,t}+\gamma r_{i,t+1}+\gamma^2 r_{i,t+2}+\cdots$を計算する。
  3. $N(s)=N(s)+1$ とする。
  4. $G(s)=G(s)+G_{i,t}$ とする。
  5. $V^{\pi}(s)=G(s)\,/\,N(s)$ とする。

$N(s)$ は用意したエピソードの集合の中で、状態 $s$ を訪問したエピソードが何個あるのかを表すカウンターです。また、$G(s)$ は各エピソードの中で初めて状態 $s$ が訪問されたときに計算した $G_{i,t}$ の合計です。$N(s)$ と $G(s)$ を用いて各状態 $s$ における未来の報酬の平均値を計算し、それを状態 $s$ の価値関数の値とします。

第2回に引き続き、火星探索ロボットに登場してもらいます。ロボットは時刻が $1$ 経過するごとに必ず左右のどちらかへ移動し、その場に留まることはありません。状態が$s_1$ のときに報酬1、状態が $s_5$ のときに報酬5をそれぞれ手にし、それ以外の状態における報酬は0です。割引率 $\gamma$ は $\gamma=0.5$ としましょう。

ロボットは状態1から状態5までをある一定の方策 $\pi$ に従って動き回ります。方策 $\pi$ に従った結果、1つ目のエピソードとして、「$s_3$→$s_4$→$s_3$→$s_4$→$s_5$」というエピソード $i$ が得られたとします。

このエピソードを用いてモンテカルロ法による方策評価を行いましょう。このエピソードの中で訪問する状態は $s_3,\,s_4,\,s_5$ですので、これらについて順に考えてみます。

まず、$s_3$ を初めて訪問する時刻は $t=1$ です。したがって、$G_{i,1}$ を計算します。

$$
\begin{align}
G_{i,1}&=r_{i,1}+\gamma r_{i,2}+\gamma^2 r_{i,3}+\gamma^3 r_{i,4}+\gamma^4 r_{i,5}\\
&=0+0+0+0+(0.5)^4\cdot5\\
&=5/16\\
&=0.3125
\end{align}
$$

これにより
$$
\begin{align}
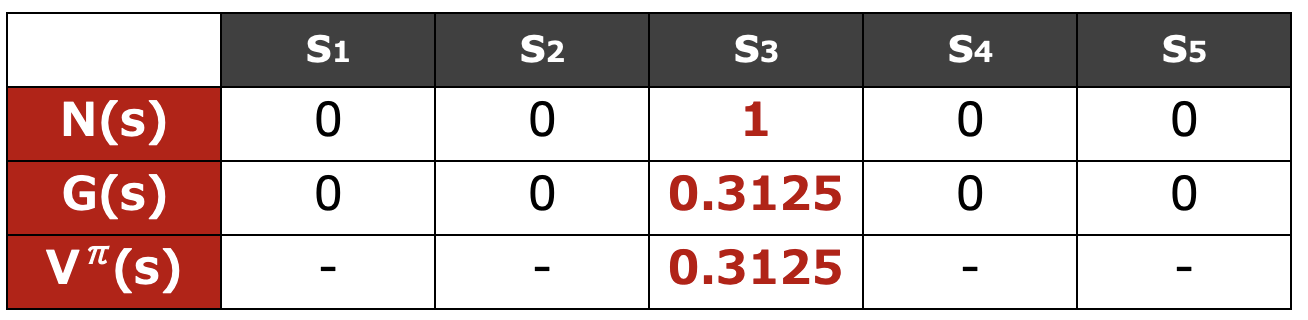
N(s_3)&=0+1=1,\\
G(s_3)&=0+0.3125=0.3125
\end{align}
$$
とそれぞれ更新できます。

$s_4$ を初めて訪問するのは時刻 $2$ なので、$s_4$ についても同様に考えると

$$
\begin{align}
G_{i,2}&=r_{i,2}+\gamma r_{i,3}+\gamma^2 r_{i,4}+\gamma^3 r_{i,5}\\
&=0+0+0+(0.5)^3\cdot5\\
&=5/8\\
&=0.625
\end{align}
$$

となり、$N(s_4)$ と $G(s_4)$ は下表のように更新できます。

最後に $s_5$ については、初めて訪問する時刻が $5$ であるため、

$$
\begin{align}
G_{i,5}&=r_{i,5}\\
&=5
\end{align}
$$

となり、このエピソード $i$ からは最終的に下表が完成します。

さらにまた他のエピソードを用いて同様の更新を繰り返すことで、状態価値関数 $V^{\pi}(s)$ を求めます。

モンテカルロ法で行動価値関数を求める際¹は、以上のような手順で計算を行います。初回訪問モンテカルロ法は偏り(bias)が全く無いというメリットがある一方で、得られる方策の分散(variance)は大きいです。言い換えると、正確な値を得るためには大量のエピソードをサンプリングする必要があります。このため、エピソードを得るのが難しい場合やエピソードのサンプリングの値段が高く付くような場合、試行錯誤による結果が重大な場合²には実用的ではありません。

逐一訪問モンテカルロ法

初回訪問モンテカルロ法は、それぞれの状態 $s$ を初めて訪問するときのみ $G_{i,t}$ を計算し、$G(s)$ と $N(s)$ を更新しました。初回訪問時のみだけでなく、すべての訪問において $G(s)$ と $N(s)$ を更新しようというのが逐一モンテカルロ法の発想です。このほかは初回訪問モンテカルロ法と全く変わりません。

$\forall s\in S$ について $N(s)=0,\,G(s)=0$ と初期化する。
$\forall i\in I$ について、以下の処理を行う。
1. エピソード内のすべての時刻 $t$ について以下の処理を行う。
  1. エピソード $i$ 内の時刻 $t$ における状態を $s$ とする。
  2. $G_{i,t}=r_{i,t}+\gamma r_{i,t+1}+\gamma^2 r_{i,t+2}+\cdots$を計算する。
  3. $N(s)=N(s)+1$ とする。
  4. $G(s)=G(s)+G_{i,t}$ とする。
  5. $V^{\pi}(s)=G(s)\,/\,N(s)$ とする。

逐一訪問モンテカルロ法は一つのエピソード内で複数回訪問した状態についても $N(s)$ と $G(s)$ の更新を繰り返します。そのため初回訪問モンテカルロ法と比較すると $N(s)$ が大きくなり、$V^{\pi}(s)$ の精度は向上します。とはいえ、今から紹介するTD学習と比較するとまだまだ正確な値を得るためには大量のエピソードを必要とする手法です。

TD学習

モンテカルロ法は方策の偏りを抑えられる一方、状態価値関数を得るためには膨大なデータが必要だという問題点がありました。

TD学習は、モデルの情報が未知な状況において、状態価値関数や行動価値関数をエピソードが終了するよりも前に更新していく手法の総称です。TD学習は一般に、方策に偏りが生じるものの、モンテカルロ法よりも分散が小さくなり素早く最適な方策に近づけるという特徴があります。

TD学習の代表的な手法としては、TD(0)学習やTD(λ)学習、SARSA、Q学習といったものが挙げられます。記事のボリューム的に今回はTD(0)学習とTD(λ)学習のみを取り上げ、SARSAとQ学習については次回扱います。なお"TD"とは、"Temporal Difference"の頭文字を取ったものです。

TD(0)学習

TD学習の中でも最もシンプルなTD(0)学習では、以下のステップで方策評価を行います。ゴールはある方策 $\pi$ のもとでの状態価値関数 $V^{\pi}(s)$ を各状態に対して求めることです。方策 $\pi$ に従った結果として得られたエピソードを1つ以上用意して、それらの集合を $I$ とします。

$\forall s\in S$ について $V^{\pi}(s)=0$ と初期化する。$\alpha\in[0,\,1]$ を決める。
$\forall i\in I$ について、以下の処理を行う。
1. エピソード $i$ 内のすべての時刻 $t$ について、以下の処理を行う。
  1. 遷移を表すタプル $(s_t,\,a_t,\,r_t,\,s_{t+1})$ をエピソード $i$ の中から取る。
  2. $V^{\pi}(s_t)=V^{\pi}(s_t)+\alpha([r_t+\gamma V^{\pi}(s_{t+1})]-V^{\pi}(s_t))$ と更新する。

2.1.2の更新式の意味が少し取りにくいですが、この式を(1)とすると式(1)は以下の式(2)に変形できます。
$$
\begin{align}
V^{\pi}(s_t)&=V^{\pi}(s_t)+\alpha([r_t+\gamma V^{\pi}(s_{t+1})]-V^{\pi}(s_t))\tag{1}\\
V^{\pi}(s_t)&=(1-\alpha)V^{\pi}(s_t)+\alpha([r_t+\gamma V^{\pi}(s_{t+1})])\tag{2}
\end{align}
$$
「もともと保持していた $V^{\pi}(s_t)$ の値」と、「遷移後の状態が保持していた $V^{\pi}(s_{t+1})$ の値と実際に得られた報酬から予測できる $V^{\pi}(s_t)$ の値」の重み付き平均を次なる $V^{\pi}(s_t)$ として採用しているわけです。

なお、このときの更新差分である
$$
\delta_t=r_t+\gamma V^{\pi}(s_{t+1})-V^{\pi}(s_t)
$$
のことを、TD誤差と呼びます。

モンテカルロ法ではエピソードの終点までの報酬を考慮したのに対し、TD(0)法では次の状態までの報酬のみを考慮しています。3つの状態を遷移するエピソードが与えられたとき、状態を$s$、行動を $a$ と表せば、2つの手法の違いは以下の図のように表現できます。オレンジ色の背景の部分がモンテカルロ法における状態価値関数の更新で考慮する範囲、黄色の背景の部分がTD(0)法における状態価値関数の更新で考慮する範囲です。

モンテカルロ法が終点まで考慮しているのに対し、TD(0)法は次に遷移する状態までのみを考慮していることがポイントです。なお、どちらの手法もエピソードに沿って価値関数を更新するため、エピソードの中で遷移しなかった部分については考慮していません。

TD(λ)学習

TD(0)学習では直後に遷移する状態のみを更新に用いましたが、エピソードがその後も続くのであれば直後よりも後にある遷移の情報も考慮したほうが効率良く学習できそうです。TD(λ)学習はこのような発想に基づいた、エピソードの終点まで考慮するモンテカルロ法と直後の遷移のみを考慮するTD(0)学習の中間を取った方法です。

まずは、$G_t$ を拡張した $G^{(n)}_t$ を以下で定義します。

$$
\begin{align}
G^{(1)}_t&=R_{t+1}+\gamma V(s_{t+1})\\
G^{(2)}_t&=R_{t+1}+\gamma R_{t+2} +\gamma^2 V(s_{t+2})\\
G^{(n)}_t&=R_{t+1}+\gamma R_{t+2} +\gamma^2 R_{t+3}+\cdots+\gamma^{n-1} R_{t+n}+\gamma^n V(s_{t+n})
\end{align}
$$

ここで、TD(0)学習における以下の更新式を改良することを考えます。
$$
\begin{align}
V^{\pi}(s_t)&=V^{\pi}(s_t)+\alpha([r_t+\gamma V^{\pi}(s_{t+1})]-V^{\pi}(s_t))\\
\end{align}
$$
上の更新式は直後の遷移しか考えていませんが、先程導入した $G^{(n)}_t$ を用いれば、例えば

$$
\begin{align}
V^{\pi}(s_t)&=V^{\pi}(s_t)+\alpha(G^{(2)}_t-V^{\pi}(s_t))\\
V^{\pi}(s_t)&=V^{\pi}(s_t)+\alpha(G^{(4)}_t-V^{\pi}(s_t))\\
V^{\pi}(s_t)&=V^{\pi}(s_t)+\alpha(G^{(4)}_t-V^{\pi}(s_t))\tag{3}
\end{align}
$$
といったように改良できそうですね³。一方で、最も上手く学習ができるような $n$ を選ぶのは簡単ではありません。そこで、すべての $n$ に渡って $G^{(n)}_t$ の加重平均を取った値 $G^{\lambda}_t$ を更新に用いましょう、というのがTD(λ)のアイディアです。$\lambda\in[0,\,1]$ に対して $G^{\lambda}_t$ は以下のように定義されます。

$$
G^{\lambda}_t=(1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}G^{(n)}_t
$$

これを用いて、TD(0)の更新式を

$$
V^{\pi}(s_t)=V^{\pi}(s_t)+\alpha(G^{\lambda}_t-V^{\pi}(s_t))
$$

と改善したのがTD(λ)学習です。$G^{\lambda}_t$ の計算時に $n$ が無限まで足し算しているので、モンテカルロ法と同様にエピソードは有限である必要があります。$\sum$ の係数に $1-\lambda$ がついているのは、$G^{n}_t$ の係数の総和を $1$ にするためです。

また、このような更新手法は「ある状態よりもあとの状態を更新に利用する」ことから、Foward View TDと呼ばれます。対になる概念としてBackward View TDが存在しますが、こちらの解説は本稿では省略します。

おわりに

モンテカルロ法と、TD(0)学習、TD(λ)学習について扱いました。特にTD(λ)学習の更新式は一見複雑ですが、TD(0)学習の自然な改良となっていることが分かれば飲み込みやすいと思います。今回は、モデルフリーの状況で状態価値を推定する方法について扱いました。次回は同じ状況下で方策を改善する手法として、モンテカルロ法を用いた方法やSARSA、Q学習について扱う予定です。

訳出について

専門用語は以下のように訳出しています。機械学習分野はしっかりとした和訳が確立されていないものも多いので、そのようなものは英語のままにしました。

日本語	英語
初回訪問モンテカルロ法	First-Visit Monte Carlo
逐一訪問モンテカルロ法	Every-Visit Monte Carlo
偏り	bias
分散	variance
TD誤差	TD error

参考文献

Sutton & Barto, "Reinforcement Learning: An Introduction", http://incompleteideas.net/book/the-book.html （最終閲覧: 2022/11/07）
sconeman, "強化学習理論の基礎2", https://qiita.com/sconeman/items/b1aacfa924e52102e9d612 （最終閲覧: 2022/11/07）
Wikipedia, "強化学習", https://ja.wikipedia.org/wiki/%E5%BC%B7%E5%8C%96%E5%AD%A6%E7%BF%92 （最終閲覧: 2022/11/07）
(画像素材) Unsplash, https://unsplash.com/ （最終閲覧: 2022/11/07）

なお、内容の説明にはLeibniz Universität HannoverのMarius Lindauer先生の講義を参考にしています。

モンテカルロ法を用いて方策を改善する方法は第4回で紹介します。 ↩
火星探査は難しそうですね。他にも、患者へ薬を投与する時の状態観察に強化学習を適用する場合なども、モンテカルロ法の適用は難しいでしょう。 ↩
(3)式のように改良すればモンテカルロ法です。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up