はじめに

前回は、モデルフリーな状況において状態価値を推定する方法を紹介しました。第4回である本稿では、モデルフリーな状況において最適な方策を得るための手法として、モンテカルロ法を用いた方法やSARSA、Q学習について紹介します。どちらも、ベーシックな強化学習では有名な手法です。なお、強化学習にはSutton & Bartoによるバイブル的な参考書"Reinforcement Learning: An Introduction"があり、この記事もここに書かれている内容を元に作成しています。すべて英語ですが、参考にしてください。

前回 ▶ 【強化学習】第3回 - モンテカルロ(MC)法とTD(0)学習、TD(λ)学習について解説
次回 ▶ 【強化学習】第5回 - 強化学習における線形関数近似について解説（執筆中）

モデルフリーにおける方策反復

モデルフリーな状況において、最適な方策を得るための手段について考えます。前回扱った方策評価を用いて方策反復の要領で学習を行うことができそうですが、遷移確率が未知なため $V^{\pi}(s)$ だけが求まったとしても状態 $s$ における最適な行動はわからず、方策は改善できそうにありません。

状態価値ではなく状態行動価値を求めるようにすることで、方策反復の要領でモデルの情報が未知な場合にも最適な方策を探すことができます。ここではまずモンテカルロ法を用いた、モデルフリーな状況における方策反復を説明します。

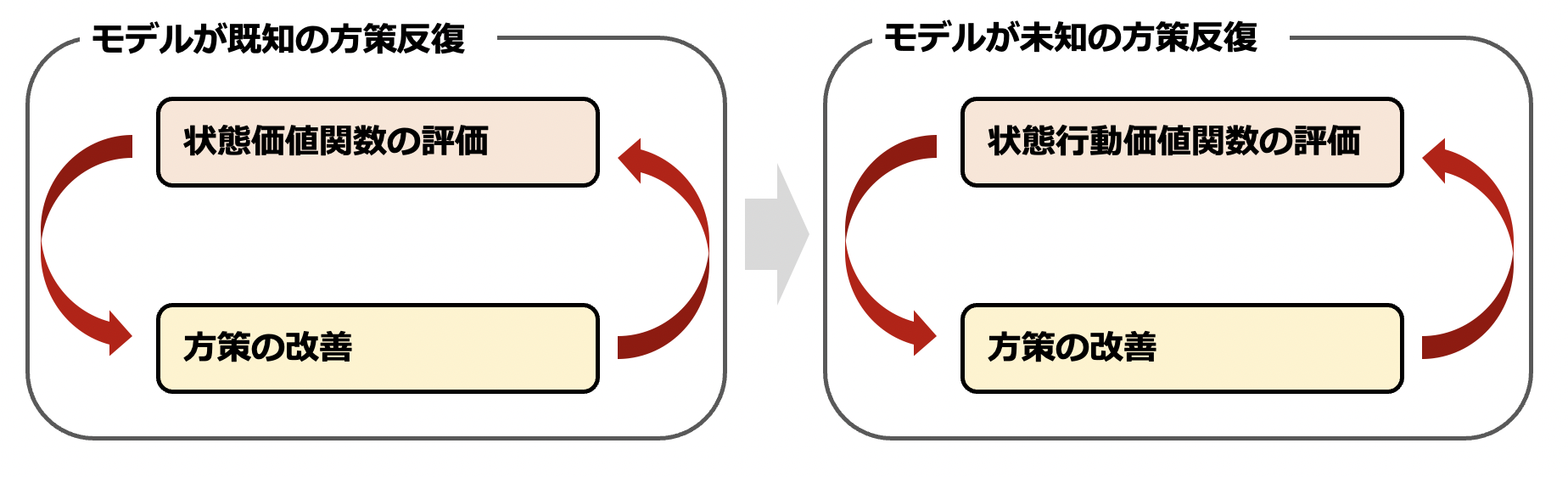
なお、第2回で既に述べている通り「ある方策に従った際の状態行動価値 $Q^{\pi}(s,\,a)$ をモンテカルロ法によって求める」→「$Q^{\pi}(s,\,a)$ を用いて方策を改善する」という流れを何度も繰り返すことを方策反復といいます。実際に方策反復を実施する際は、以下で述べる「モンテカルロ法」のアルゴリズムと「方策改善」のアルゴリズムのセットを何度も繰り返すことになります。

モンテカルロ法

モデルフリーの場合では、例えば初回訪問モンテカルロ法を状態行動価値の推定に適用することが考えられます。アルゴリズムは以下の通りです。予め、方策 $\pi$ に従って得られるエピソードをサンプリングしておきます。

$\forall s\in S,\,a\in A$ について $N(s,\,a)=0,\,G(s,\,a)=0,\,Q^{\pi}(s,\,a)=0$ と初期化する。
サンプリングしたエピソード $i=s_{i,1},\,a_{i,1},\,r_{i,1},\,s_{i,2},a_{i,2},\,r_{i,2},\,\cdots,\,s_{i,T_i}$ について以下を繰り返す。
1. エピソード $i$ の中で現れる任意の「状態と行動の組」 $(s,\,a)$ について、以下の処理を行う。
  1. エピソード $i$ の中で初めて $(s,\,a)$ の組が現れる時刻 $t$ を選ぶ。
  2. $G_{i,t}=r_{i,t}+\gamma r_{i,t+1}+\gamma^2 r_{i,t+2}+\cdots$ を計算する。
  3. $N(s,\,a)=N(s,\,a)+1$ とする。
  4. $G(s,\,a)=G(s,\,a)+G_{i,t}$ とする。
  5. $Q^{\pi}(s,\,a)=G(s,\,a)\,/\,N(s,\,a)$ とする。

「状態と行動の組」とは同じ時刻に現れる状態と行動の組、例えば $(s_{i,1},\,a_{i,1})$ や $(s_{i,2},\,a_{i,2})$ を指します。もちろん、このアルゴリズムを逐一訪問モンテカルロ法の要領で書き換えることも可能です。

方策改善

モデルが既知の場合と同様に方策改善を行いましょう。今回は $Q^{\pi}(s,\,a)$ が直接求まっているため、方策改善では単に最も大きな値を与える行動 $a$ を選択するという貪欲な方策を採用します。改善前の方策を $\pi_i$ とすると、改善後の方策 $\pi_{i+1}$ は
$$
\pi_{i+1}(s)\in \underset{a\in A}{\rm{argmax}}\,Q^{\pi_i}(s,\,a)
$$
と表すことができます。

方策反復の例と問題点

方策反復の例を見てみましょう。例によって火星探索ロボットを考えますが、今回は状態①の報酬が $999$ と極端に高く、状態⑤の報酬が $5$、残りの状態の報酬は $0$ であるような場合を考えます。

第3回で紹介したモンテカルロ法の際と同様に、方策 $\pi_0$ に従った際のエピソードとして「③→④→③→④→⑤」が得られたとします。

このとき、行動と状態を表にまとめると以下のようになります。左へ移動するという行動を $L$、右へ移動するという行動を $R$ としています。

ゆえに、割引率 $\gamma=0.5$ として初回訪問モンテカルロ法による状態行動価値関数の評価を行うと、
$$
\begin{align}
Q(3,\,R)&=0+0+0+0.5^3\cdot5=0.625\\
Q(4,\,L)&=0+0+0.5^2\cdot5=1.25\\
Q(4,\,R)&=5
\end{align}
$$
の $3$ つが求まります。残りの $Q(s,\,a)$ はすべて $0$ のままです。

したがって、新たな方策として下表の最下段のような方策が得られます。ピンク色は各状態における最大の報酬が期待できる行動、青色は最大の報酬が期待できなかった行動です。

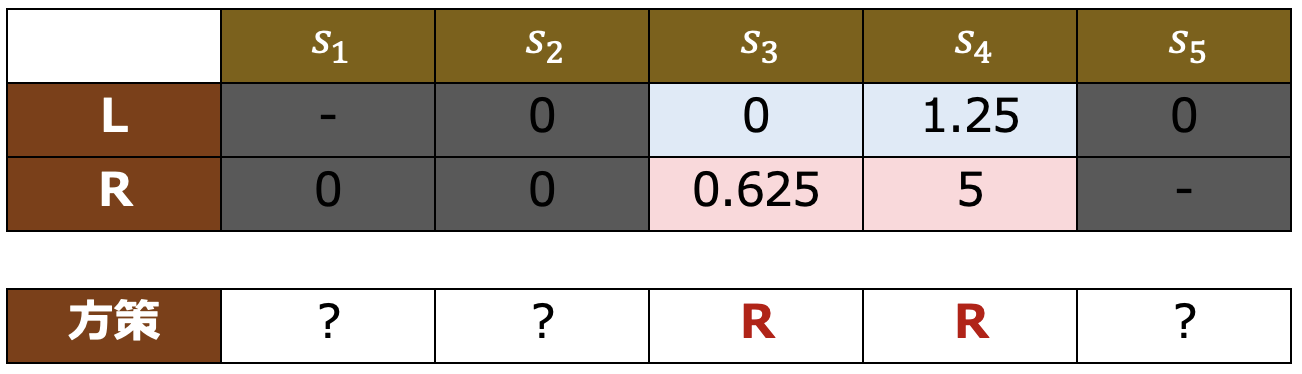
次はこの方策に従ってエピソードをサンプリングすることになります。ところで、現時点で得られているこの方策は合理的でしょうか？　また、同じようにサンプリングと改善の流れを繰り返せば、しっかりと最適な方策にたどり着くのでしょうか？

答えはどちらも「いいえ」ですね。状態①の報酬 $999$ を獲得するためには、状態③から左へ動くという行動も試してみる必要があります。しかし、方策が決定的な場合、このような試行錯誤は発生しません。これが貪欲な方策の問題点です。

ε-greedy方策

それでは、先程の問題点を改善するためにはどうすればよいのでしょうか。

問題は、方策が常に決定的な選択を行うという点にあります。方策に確率的な要素を取り入れることで、適度に探索も織り交ぜてこの問題を解決しようというのがε-greedy方策のアイディアです。

状態行動価値関数 $Q(s,\,a)$ が与えられたとき、以下のような確率分布 $\pi(a\,|\,s)$ のことをε-greedy方策といいます。

確率 $\epsilon$ で完全にランダムに行動を決定する
確率 $1-\epsilon$ で $\underset{a\in A}{\rm{argmax}}\,Q(s,\,a)$ を選択する

基本的には現在の $Q(s,\,a)$ に基づいて最も報酬が高くなりそうな行動を選択するが、たまに全くランダムに行動を決定する、というイメージですね。$\epsilon$ が大きくなればなるほど未知の領域のランダムな探索を積極的に行いますが、学習がなかなか進まなくなるというデメリットがあります。一方で $\epsilon$ 小さくなればなるほど速く方策を学習しますが、先述したような「本当に価値のある状態の見落とし」が起こりやすくなってしまうというデメリットがあります。

モデルフリーにおける価値反復

方策反復の要領で、「方策 $\pi$ に従ったときの状態行動価値観数を求め、方策を改善する」というループを繰り返すと、モデルが既知の場合と同様に計算効率が悪そうです。ここからは、モデルフリーな状況における価値反復の手法として有名なSARSAとQ学習について説明します。

用語の準備

SARSAとQ学習の説明に入る前に、ここでいくつかの用語をまとめて説明しておきます。

方策オンと方策オフ

先程説明した方策反復による学習においては、まず一定の方策 $\pi$ に従った結果得られたエピソードをサンプリングしました。そして、方策 $\pi$ に従ったときの状態価値関数を求め、方策 $\pi$ の良さを求めました。

このように、サンプリングする際の方策と、良さを評価する方策が同じ場合の学習を、方策オンである、といいます。反対に、サンプリングする際の方策と良さを評価する方策が異なる場合の学習は、方策オフである、といいます。また、方策オフ学習の際には実際の振る舞いを示す方策のことを、"Behavior Policy"、良さを評価したい方策のことを"Current Policy"と呼び、それぞれ $\pi_b$、$\pi^{*}$ で表すことがあります。

GLIE

ある探索方法が以下の2条件を満たすとき、その探索方法はGLIEである、といいます。

考えうる任意の状態と行動の組 $(s,\,a)$ について
$$
\lim_{i\to\infty}N_i(s,\,a)\to\infty
$$を満たす。
Behavior Policyが必ず
$$
\forall s\in S\quad\lim_{t\to\infty}\pi(a\,|\,s)\to\underset{a\in A}{\rm{argmax}}\,Q(s,\,a)
$$を満たす。

すなわち、すべての行動と状態の組が無限回探索されるような探索方法で、かつその探索方法によって得られる方策がすべての状態に対して貪欲であるような場合、その探索方法はGLIEである、ということです。ちなみに、GLIEは"Greedy in the Limit of Infinite Exploration"の略です。「無限の探索の極限において貪欲である」という概念そのままの名前ですね。

Robbins-Munro sequence

ある数列 ${a_n}$ が以下の2つの条件を満たすとき、${a_n}$ はRobbins-Munro sequenceであるといいます。
$$
\sum_{t=1}^{\infty}a_t=\infty\\
\sum_{t=1}^{\infty}a_t^2<\infty
$$
例えば $a_n=1\,/\,n$ はRobbins-Munro sequenceです。

SARSA

SARSAは、モデルフリーの際に用いられる方策オン型の学習方法です。まずはSARSAのアルゴリズムを見てみましょう。

方策 $\pi$ をε-greedyになるように初期化する。$\forall s\in S,\,\forall a\in A$ に対して $Q(s,\,a)=0$ と初期化する。$t=0$ とし、現在の状態 $s_t$ を $s_t=s_0$ とセットする。
以下を繰り返す。
1. 方策 $\pi(s_t)$ に従って、行動 $a_t$ を選び行動する。
2. 報酬 $r_t$ と、次の時刻の状態 $s_{t+1}$ を観測する。
3. 方策 $\pi(s_{t+1})$に従って、行動 $a_{t+1}$ を選ぶ。
4. 得られた $(s_t,\,a_t,\,r_t,\,s_{t+1},\,a_{t+1})$ に基づいて以下のように状態行動価値関数 $Q$ を更新する。
  $$
  Q(s_t,\,a_t)=Q(s_t,\,a_t)+\alpha(r_t+\gamma Q(s_{t+1},\,a_{t+1})-Q(s_t,\,a_t))
  $$
5. $\pi(s_t)$ を、確率 $1-\epsilon$ で $\pi(s_t)\in\underset{a\in A}{\rm{argmax}}\,Q(s_t,\,a)$、確率 $\epsilon$ でランダムに行動を選ぶような確率分布に更新する。
6. $t=t+1$ とする。

TD学習の際のアルゴリズムにε-greedyの要素を取り入れ、評価対象を状態価値関数ではなく状態行動価値関数にしたというイメージです。2.4で$(s_t,\,a_t,\,r_t,\,s_{t+1},\,a_{t+1})$ という列が出てくることから、SARSAと呼ばれています。

なお、$\alpha$ については定数ではなく、時刻に依存する $\alpha_t$ に置き換えるという改良を行うことができます。この際、数列 ${\alpha_t}$ がRobbins-Munro sequenceであるとき、SARSAは最適な状態行動価値関数に収束することが知られています。

SARSAの例

状態①の極端な報酬を元に戻し、再び火星探索ロボットに登場してもらいましょう。SARSAのアルゴリズムより、今回は状態①からスタートです¹。初めはε-greedy方策をセットしますが、まだ状態行動価値関数についての情報がないため、例えば状態①から順に「基本的に $R,\,R,\,R,\,R,\,L$ をそれぞれ選択する」ような方策からスタートするとしましょう。ここで「基本的に $L$ を選択する」とは、「ε-greedy「確率 $1-\epsilon$ で $L$ を選択し、確率 $\epsilon$ で $L$ と $R$ からランダムに行動を選択する」ということを指します²。$R$ についても同様です。また$\alpha_t$ は $\alpha_t=1\,/\,(t+1)$ とし、$\epsilon=0.2,\,\gamma=0.5$ とします。

例えば $\epsilon=0.2$ で「基本的に $L$ を選択する」という戦略に従うとき、実際に $L$ を選択する確率は $0.8+0.2\cdot 1\,/\,2=0.9$ となります。

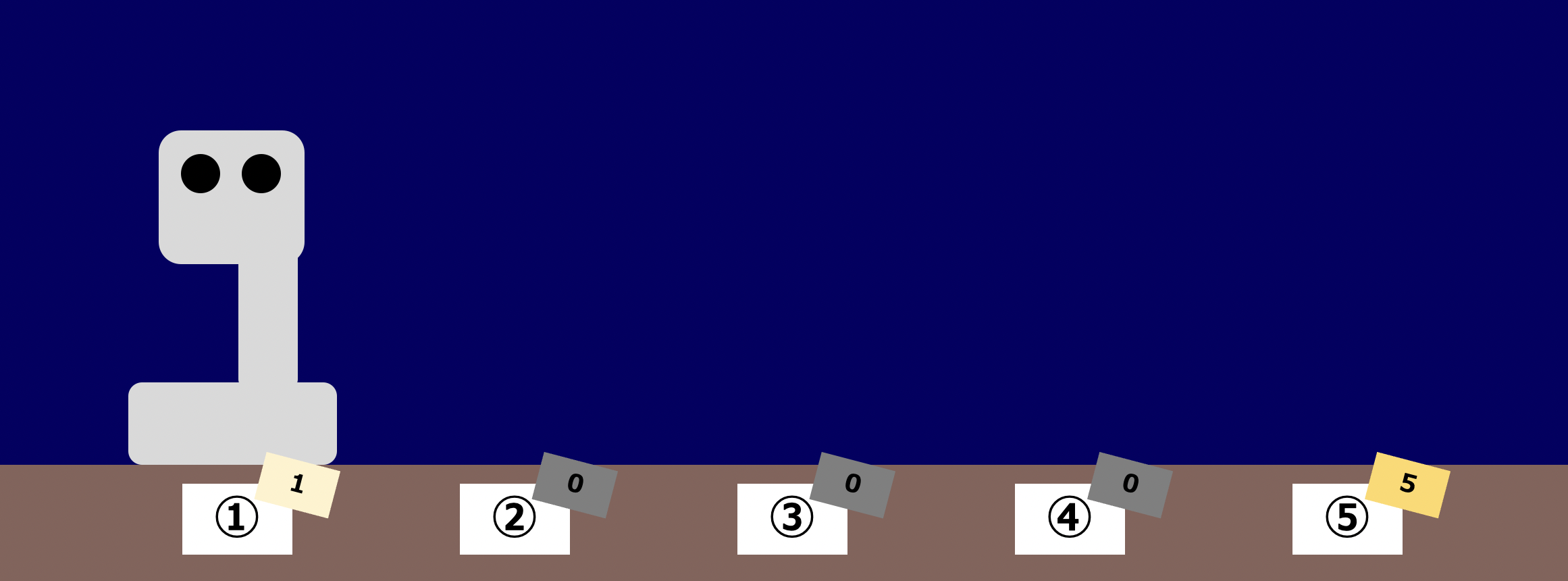
この方策に従った際の時刻 $0$ における行動として $R$ が得られるため、この行動を実施します。この行動を取った結果、ロボットは状態②へ移動することができたとします。移動先である状態②では報酬を獲得できないため、時刻 $0$ における報酬は $0$ です。さらに、時刻 $0$ 時点での方策に従って、状態②における行動をシミュレーションしてみましょう。「基本的に $L$」という方策に従ってランダムに決定した結果、ここでは $L$ を選択したとします。

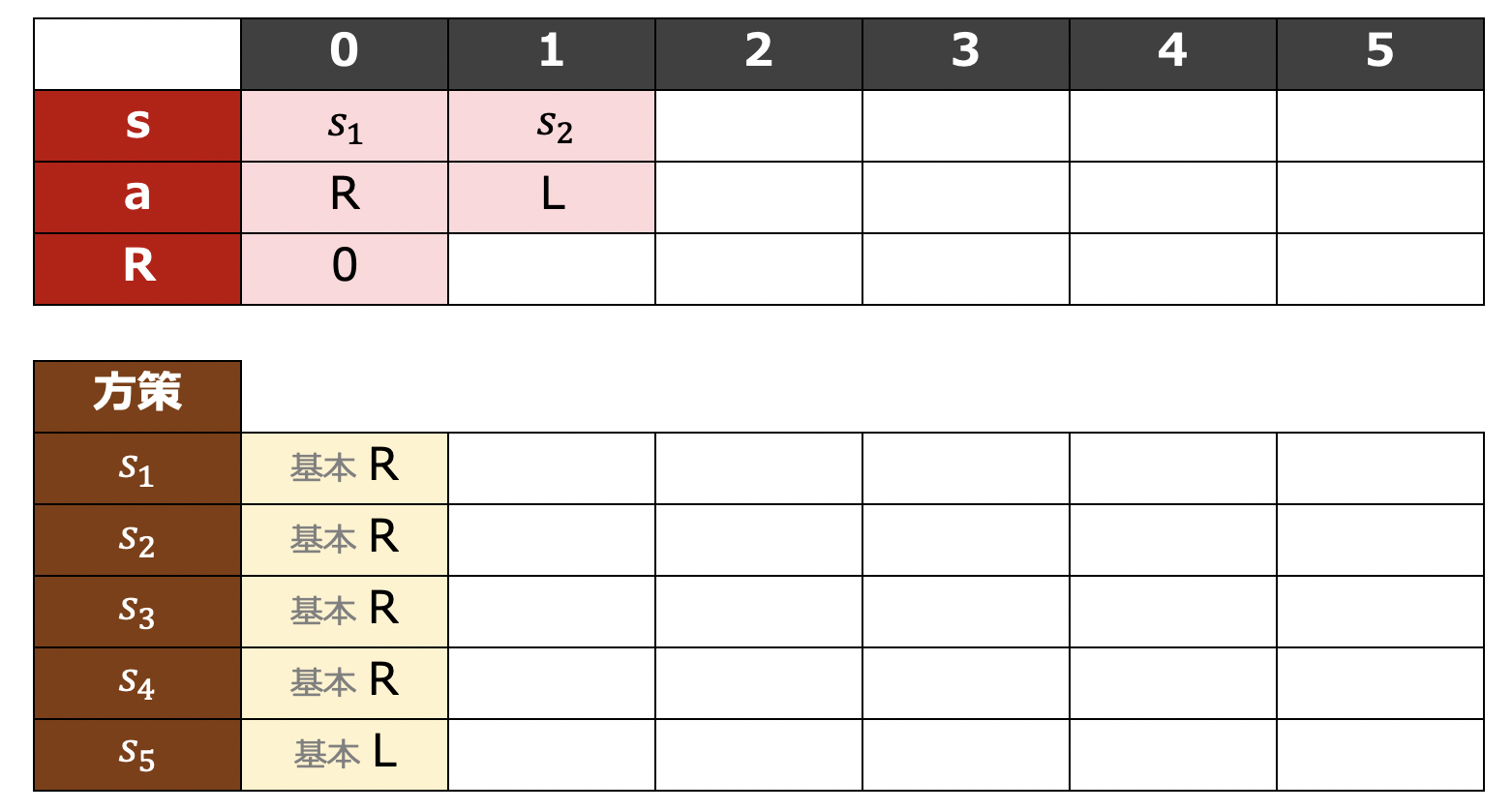
更新に用いる情報があるマスをピンク色で塗りつぶすと上のようになります。$(s,\,a,\,r,\,s,\,a)$ の組が更新に用いられているのが分かりやすいです。

SARSAのアルゴリズムに従えば、 $Q(s_1,\,R)$ は以下のように更新することができます。

$$
\begin{align}
Q(s_1,\,R)&=Q(s_1,\,R)+\alpha(r_0+\gamma Q(s_{2},\,L)-Q(s_1,\,R))\\
&=Q(s_1,\,R)+\dfrac{1}{1}(0+0.5\cdot Q(s_2,\,L)-Q(s_1,\,R))\\
&=0.5\cdot Q(s_2,\,L)\\
&=0
\end{align}
$$

$Q(s_1,\,R)$ を更新したので、状態 $s_1$ に関する方策 $\pi(s_1)$ を更新します。本来はここでとり得る行動 $a$ に対する $Q(s_1,\,a)$ を比較することになりますが、今回は状態 $s_1$ で行動 $R$ しか取れないため、「基本的に $R$」という方策は変わりません。

次に、更新後の時刻 $1$ における方針にしたがって行動を選択してみましょう。ここでは「基本的に $R$」という方針に従った結果、たまたま確率が低い方の行動 $L$ を実施したとします。観測される報酬は $1$ です。また、行動実施後に状態 $s_1$ へ移動したとします。状態 $s_1$ における「基本 $R$」という方策に従った結果、行動 $R$ を選択したとしましょう。

よって、SARSAのアルゴリズムに従うと $Q(s_2,\,L)$ は次のように更新できます。

$$
\begin{align}
Q(s_2,\,L)&=Q(s_2,\,L)+\alpha(r_1+\gamma Q(s_{1},\,R)-Q(s_2,\,L))\\
&=Q(s_2,\,L)+\dfrac{1}{2}(1+0.5\cdot Q(s_1,\,R)-Q(s_2,\,L))\\
&=0.5\cdot Q(s_2,\,L)+0.5+0.25\cdot Q(s_1,\,R)\\
&=0+0.5+0\\
&=0.5
\end{align}
$$

$Q(s_2,\,L)$ を更新したため、状態 $s_2$ に関する方策 $\pi(s_2)$ を更新します。$Q(s_2,\,L)=0.5$ と $Q(s_2,\,R)=0$ を比較すると、状態 $s_2$ においてより大きな報酬が期待できるのは行動 $L$ です。したがって、方策 $\pi(s_2)$ を「基本的に$L$」と更新することができます。

今は$s_2$ において、$s_1$ を目指す方向に学習が進んだ、ということになります。局所最適解に陥ってしまっているように思うかもしれませんが、適切にパラメータを調整すれば、学習を重ねることで徐々に $s_5$ を目指す方策へ変化していきます。これがε-greedy方策による探索の強みです。

Q学習

SARSAが方策オン型であったのに対し、Q学習はモデルフリーの際に用いられる方策オフ型の学習方法です。ほとんどアルゴリズムはSARSAと変わりませんが、次の時刻での行動を観測せず、次の時刻における状態行動価値関数の最大値を更新に用いています。

方策 $\pi_b$ をε-greedyになるように初期化する。$\forall s\in S,\,\forall a\in A$ に対して $Q(s,\,a)=0$ と初期化する。$t=0$ とし、現在の状態 $s_t$ を $s_t=s_0$ とセットする。
以下を繰り返す。
1. 方策 $\pi_b(s_t)$ に従って、行動 $a_t$ を選び行動する。
2. 報酬 $r_t$ と、次の時刻の状態 $s_{t+1}$ を観測する。
3. 得られた $(s_t,\,a_t,\,r_t,\,s_{t+1})$ に基づいて以下のように状態行動価値関数 $Q$ を更新する。
  $$
  Q(s_t,\,a_t)=Q(s_t,\,a_t)+\alpha(r_t+\gamma\,\underset{a'\in A}{\rm{max}}Q(s_{t+1},\,a')-Q(s_t,\,a_t))
  $$
4. $\pi_b(s_t)$ を、確率 $1-\epsilon$ で $\pi_b(s_t)\in\underset{a\in A}{\rm{argmax}}\,Q(s_t,\,a)$、確率 $\epsilon$ でランダムに行動を選ぶような確率分布に更新する。
5. $t=t+1$ とする。

以上のアルゴリズムにおいて、実際の行動を示す方策 $\pi_b$ は $Q(s,\,a)$ に従うε-greedy方策、良さを評価したい方策 $\pi^{*}$ は $Q(s,\,a)$ に従うgreedy方策です。

Q学習の例

Q学習の例を見てみましょう。SARSAと同じ火星探索ロボットによる学習の状況を考えます。Q学習による学習を進めた結果、時刻 $8$ において下表のような学習結果が得られているとしましょう³。今回は、右下に時刻 $8$ における状態行動価値関数 $Q$ の値も示します。

Q学習では、まずSARSAのときと同様に時刻 $8$ における方策に従って行動を決定します。「基本 $R$」という方策に従った結果、行動 $R$ が選択され、その結果 $s_3$ へ移動したとします。このときの報酬は $0$ です。

さて、ここでSARSAでは現在の方策に従って $s_3$ における行動を考えていましたが、Q学習では次の時刻の行動を選ぶということをしません。代わりに、現在保持している $Q(s_3,\,L)$ と $Q(s_3,\,R)$ の値を参照します。このうち、大きい方は $Q(s_3,\,L)$ です。下表の緑色で示したマスを比較しています。

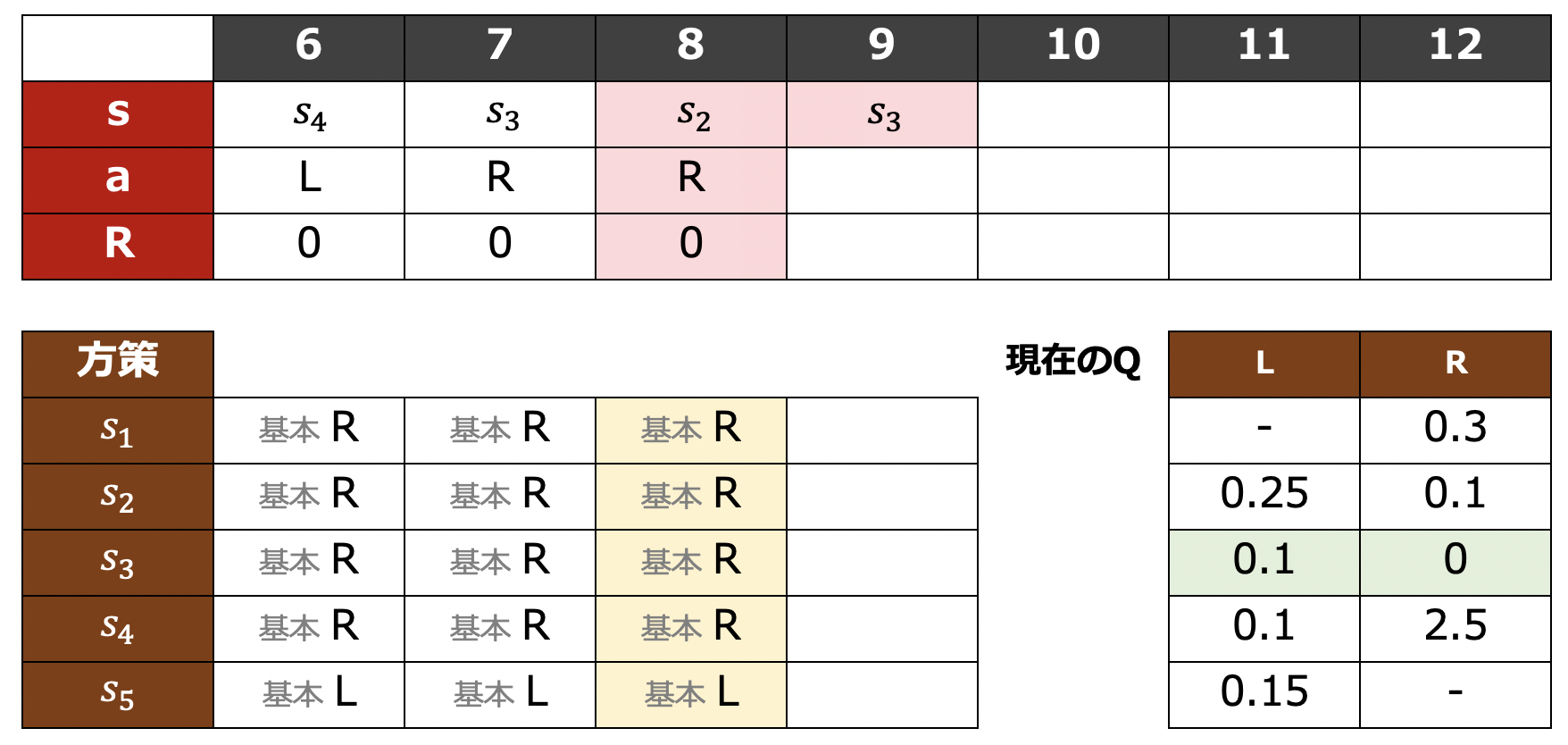
以上のことから、状態行動価値関数 $Q(s_2,\,R)$ を次のように更新します。

$$
\begin{align}
Q(s_2,\,R)&=Q(s_2,\,R)+\alpha(r_1+\gamma\,\underset{a'\in A}{\rm{max}}\, Q(s_{3},\,a')-Q(s_2,\,R))\\
&=Q(s_2,\,R)+\dfrac{1}{2}(0+0.5\cdot Q(s_3,\,L)-Q(s_2,\,R))\\
&=0.5\cdot Q(s_2,\,R)+0.25\cdot Q(s_3,\,L)\\
&=0.5\cdot0.1+0.25\cdot0.1\\
&=0.075
\end{align}
$$

この状況におけるSARSAでは高確率で次の時刻の行動が $R$ と選択されるため、更新の結果も異なりますね。

ダブルQ学習

Q学習では、方策を更新する際と状態行動価値関数を評価する際に、同じ状態行動価値関数 $Q(s,\,a)$ を用いていました。しかし、このように学習を進めると、常に次の時刻における最大値を用いるため $Q(s,\,a)$ が過大評価されてしまいます。その結果、過大評価された行動をより多く選ぶようになり、評価のズレがなかなか改善されません。

このような偏りを低減するための方法として提案されたのが、ダブルQ学習です。ダブルQ学習では、状態行動価値関数を $Q_1(s,\,a)$ と $Q_2(s,\,a)$ の2つ用意します。そして、$Q_1$ や $Q_2$ を更新する際にはお互いの情報をバランスよく用います。アルゴリズムは以下の通りです。

$\forall s\in S,\,\forall a\in A$ に対して $Q_1(s,\,a)=0,\,Q_2(s,\,a)=0$ と初期化する。$t=0$ とし、現在の状態 $s_t$ を $s_t=s_0$ とセットする。
以下を繰り返す。
1. 行動 $a_t$ を、$\underset{a\in A}{\rm{argmax}}\,Q_1(s_t,\,a)+Q_2(s_t,\,a)$ を用いてε-greedyに選択する。
2. 報酬 $r_t$ と、次の時刻の状態 $s_{t+1}$ を観測する。
3. 半々の確率で、次のうちどちらかの更新を行う。
  3.a $$
  Q_1(s_t,\,a_t)=Q_1(s_t,\,a_t)+\alpha(r_t+\gamma\,Q_2(s_{t+1},\,\underset{a'\in A}{\rm{argmax}}\,Q_1(s_{t+1},\,a'))-Q_1(s_t,\,a_t))
  $$
  3.b $$
  Q_2(s_t,\,a_t)=Q_2(s_t,\,a_t)+\alpha(r_t+\gamma\,Q_1(s_{t+1},\,\underset{a'\in A}{\rm{argmax}}\,Q_2(s_{t+1},\,a'))-Q_2(s_t,\,a_t))
  $$
4. $t=t+1$ とする。

$Q_1$ を更新する際は、「現在の時刻における$Q_1$」と「次の時刻における $Q_2$ の最大値」を用います。ただし、どの行動が次の時刻において最大値を与えるかを決める際には $Q_1$を用います。$Q_2$ を更新するときについても同様です。

たとえ $Q_1$ で過大評価された行動があったとしても、$Q_2$ においてそのような行動が同じように過大評価されている確率は低いため、評価の偏りが早い段階で吸収されやすく、純粋なQ学習よりも高速に最適な $Q$ が得られます。

おわりに

モデルフリーなときの価値反復やSARSA、Q学習について扱いました。状態が離散的なときの強化学習についてはここまでで概ねベーシックなものを網羅しました。次回は連続的な状態に話題を移し、線形関数近似について扱う予定です。

訳出について

専門用語は、以下のように訳出しています。機械学習分野はしっかりとした和訳が確立されていないものも多いので、そのようなものは英語のままにしました。

日本語	英語
方策オン	On Policy
方策オフ	Off Policy
Q学習	Q-Learning
ダブルQ学習	Double Q-Learning

参考文献

Sutton & Barto, "Reinforcement Learning: An Introduction", http://incompleteideas.net/book/the-book.html （最終閲覧: 2022/11/03）
icoxfog417, "ゼロからDeepまで学ぶ強化学習", https://qiita.com/icoxfog417/items/242439ecd1a477ece312 （最終閲覧: 2022/11/03）
(画像素材) Unsplash, https://unsplash.com/ （最終閲覧: 2022/11/03）

なお、内容の説明にはLeibniz Universität HannoverのMarius Lindauer先生の講義を参考にしています。

アルゴリズムでは $s_0$ と示しましたが、状態 $s_1$ としても同じことです。 ↩
この記事のみでの用語です。 ↩
時刻 $7$ において行動 $L$ を選択した結果、状態が $s_2$ から $s_3$ へ変化していますが、これはミスではありません。$L$ はあくまでも「左へ移動しようと試みる」というだけで、環境によってはこの行動の結果、右へ移動してしまうこともあります。あるいは、すぐ左ではなく2個左の状態へ移動してしまうこともあるでしょう。もちろんモデルフリーのアルゴリズムは、このような場合でも問題なく学習することができます。 ↩

【強化学習】第4回 - SARSAとQ学習について解説