ゼロからDeepまで学ぶ強化学習

ロボットから自動運転車、はては囲碁・将棋といったゲームまで、昨今多くの「AI」が世間をにぎわせています。

その中のキーワードとして、「強化学習」というものがあります。そうした意味では、数ある機械学習の手法の中で最も注目されている(そして誇張されている・・・)手法ともいえるかもしれません。

今回はその強化学習という手法について、基礎から最近目覚ましい精度を出しているDeep Q-learning(いわゆるドキュン、DQNです)まで、その発展の流れと仕組みについて解説をしていきたいと思います。

本記事の内容をベースに、ハンズオンイベントを開催しました(PyConJPのTalkの増補改訂版)

Pythonではじめる強化学習 OpenAI Gym 体験ハンズオン

講義資料の方が図解が豊富なので、数式とかちょっと、という場合はこちらがおすすめです。

• Tech-Circle #18 Pythonではじめる強化学習 OpenAI Gym 体験ハンズオン
• ハンズオン用GitHubリポジトリ

強化学習の特性

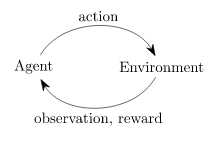
強化学習は教師あり学習に似ていますが、(教師による)明確な「答え」は提示されません。では何が提示されるかというと、「行動の選択肢」と「報酬」になります。

これだと答え=報酬と考えれば同じじゃないか(行動A=10pt、のような)、と感じると思いますが、一つ大きな違いがあります。それは強化学習においての報酬は「各行動」に対してではなく、「連続した行動の結果」に対して与えられるという点です。
サッカーでたとえると、ゴールをしたら1点、というのは強化学習における報酬になります。ただ、ゴールに至るためにパスをする、ドリブルをする、という各行動についてはいちいち報酬が与えられません。逆に、コートの外から「今のパスはいいぞ！」「そこでドリブルしたらダメだろ！」と逐一指示が飛んでくるのが教師あり学習になります。強化学習では「連続した行動の結果」としてのゴールの1点しか報酬が与えられないため、それに至るためのパスやドリブルがどれぐらいいいのかは、ゴールできたケースとできなかったケースから、自分自身で「評価」を行っていく必要があります。

では、どうやって各行動を「評価」していくのか。
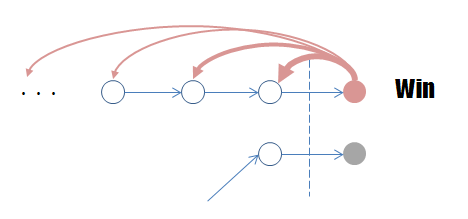
まず、ゴールした瞬間の行動(最後のシュート)には、報酬が入ります(1点)。では、その一つ手前の行動はどうでしょうか。これも、最後にゴールを決めるためのお膳立てをしたわけですから、なかなかに良い行動だったのではないかと思えます。ではその前の・・・と逆算していくと、最後の行動から遡って各行動を評価できます。

強化学習では、このように「連続した行動の結果」に対する報酬から、各行動の「評価」を自分自身で更新します。これにより、各行動に対する報酬を逐一設定しなくても、自らの評価を基に最終的に報酬が得られる連続した行動を学習してくれるというわけです。
将棋や囲碁のような複雑なゲームの場合、どの場面でどの手が最善なのかは意見が分かれることもありますし、ましてその報酬を何ポイントにすべきかなど輪をかけて難しくなります。そうした場合でも最後の勝ち負けは明確であるため、強化学習を適用することで行動評価の難しさをスキップして、最終的に勝つ行動を学習させることができます。そのため、強化学習は教師あり学習よりも一般的に複雑な問題を扱うことができます。

ただ、この点をもって強化学習が教師あり学習より上等な手法である、というわけではない点に注意してください。逆に言えば強化学習は明確な指示がない状態で自分自身の中での「行動に対する評価」を獲得していかなければならないということで、これにはとても時間がかかります。ゴールという結果に至るまでの行動の数、またその組み合わせの数は膨大であり、最適化には多くの時間がかかります(コンピューターが計算速いとはいえ)。また、強化学習が獲得した「行動に対する評価」が人間から見て合理的な保障もどこにもありません。
きちんと先生がいるのと、独学するのでは前者の方が効率がよく最適解にたどり着きやすいのは明らかなので、学習方法は、扱う問題に応じて適切に選ぶ必要があります。

以上が、強化学習の特性になります。続いては、これをモデル化しその学習方法について解説していきます。

強化学習のモデル化(Markov Decision Process)

強化学習が対象とする問題を、以下のようにモデル化します。

• States: S
• 状況。ゲームでいえば、特定の局面を表す
• Model: T(s, a, s') (=P(s'|s, a))
• TはTransitionで、状況sの時に行動aをとると状況s'になる、ということ。ただし、aを選択しても発動しなかったり別のところに行ったり、といった状況を表現するため確率的な表現(P(s'|s, a))になる
• Actions: A(s), A
• 行動。状況によって取れる行動が変わる場合は、A(s)といった関数になる
• Reward: R(s), R(s, a), R(s, a , s')
• 状況、またその状況における行動から得られる報酬。この報酬は、最後の結果以外は自己評価になります(即時報酬)。
• Policy: $\pi(s)$ -> a
• 戦略。状況sにおいてどういう行動aを取るべきか、を返す関数。

このモデル化をMarkov Decision Process(MDP、マルコフ決定過程)といいます。マルコフというのはマルコフ性という意味で、$\pi(s)$で表されるように次の行動には現在の状態(s)しか関与しないという性質を表します。

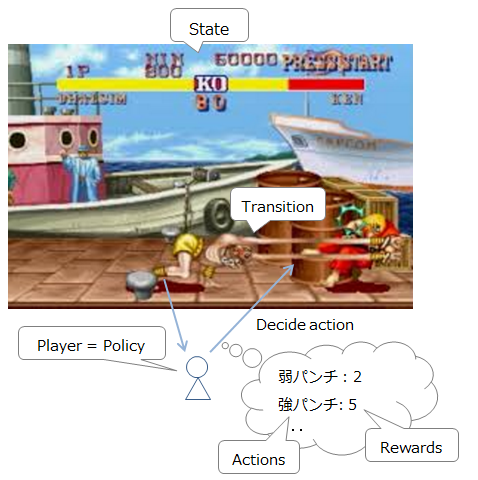
ストリートファイター的に説明すると、以下のような感じです。

• 現在の状況(敵・自分の位置及びHP): State
• 現在入力可能なコマンド: Actions
• 移動・攻撃etc: T(s, a, s')　入力可能なコマンドとその発動確率の一覧(ヨガファイアを出そうとしてもコマンドをミスることがあるため、確率的になる)
• プレイヤー(意思決定者): Policy
• 行動により得られる報酬: Reward

※なお、「機械学習で最強のスト２戦士を作って欲しいと思った」というコメントを頂きましたが、すでにAIの戦闘能力は一般人を上回っており、逆に「いかに手加減するか」が課題となっています(参考)。人類は鍛錬に励む必要があります。

さて、ストリートファイトにおいては相手のHPを削るのが勝つための最短経路になりますが、パンチばっかりしても最終的に勝利するのが難しいことは明らかです。よって、戦略の最適化のためには短期ではなく、長期における報酬の最大化を行う必要があります。

ただ、長期といっても時間が無限なら、なるべく遠くからズームパンチ(上図参照)が一番効率的な戦略になります。時間が無限にあるなら危険を冒して近づいてヨガフレイムをするよりは、与えられるダメージは少なくとも相手に近寄らない方策を取った方が無難なためです。
このように時間が無限の場合低リスクローリターンな行動に偏りがちなるため、時間による割引の概念を導入します。つまり、さっさと行動しないと同じ行動でも得られる報酬がどんどん減るようにするということです。

つまり、戦略を最適化するためには以下の2点が重要になるということです。

• 報酬の総和を最適化するようにする
• 時間に対する、報酬の割引を導入する

これを式で表すと、以下のようになります。

$$
U^{\pi}(s) = E \left[ \sum_{t}^{\infty} \gamma^{t} R(s_t) | \pi, s_0=s \right]
$$

• 報酬の総和=$U^{\pi}(s)$: 状態$s$から戦略$\pi$を行う場合($\pi, s_0=s$)の、報酬の総和
• 時間に対する割引=$\gamma$: $0 \leq \gamma < 1$で、概ね1に近い値

この「時間割引を考慮した報酬の総和」を最大化する戦略を発見するのが目指すところになります。この最適な戦略を$\pi^*$とします。
最適な戦略においては、基本的には報酬が最大になるように行動するはずです。これは、数式的に以下のように表現できます。

$$
\pi^{*}(s) = argmax_a \sum_{s'} T(s, a, s') U(s')
$$

$argmax$は最大のものを選ぶ、という意味です。つまり$s$からの遷移先である$s'$のうち、期待される報酬の総和$U(s')$が最大の$s'$を目指して行動するということです。結局のところ最適な戦略$\pi^*$とは、どんな$s$でもそこからの報酬の総和が最大になるような行動をとるということになるので、最初に定義した$U^{\pi}(s)$を以下のように書き直せます。

$$
U(s) = R(s) + \gamma max \sum_{s'} T(s, a, s') U(s')
$$

この等式をBellman equationと言います。わざわざこのように書き直したのは、こうすることで式から戦略$\pi$を追い出せたので、「選択している戦略によらずその報酬を計算する」ことができるようになるからです。つまり、ゲーム設定(環境)のみから最適な行動を計算できるということです。これが、モデルを学習させるためのキーアイテムになります。

モデルの学習

ここからは、上記で構築したモデルをどのように学習させるのかについて解説していきます。

Value Iteration

先ほど導出したBellman equationを利用し、さっそく「環境のみから」最適な行動を計算してみます。この計算では、最初のセクションで解説した通り、「最後の報酬」が得られた状態から遡って繰り返し計算をしていきます。この繰り返しの計算を、Value Iterationと呼びます。

以下で、パックマンの例をとってValue Iterationの様子を図示しています。

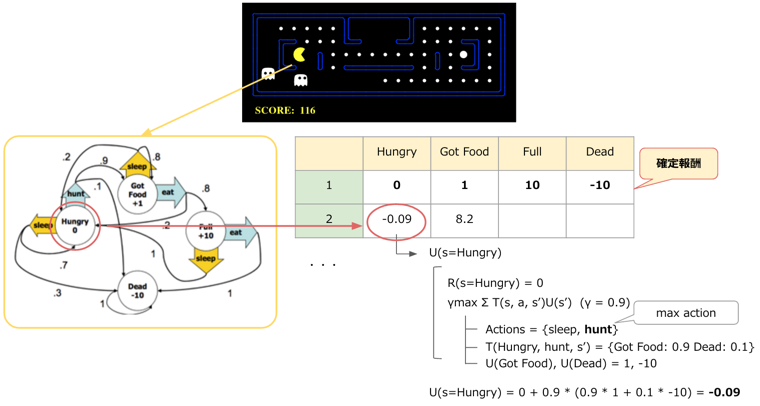
Markov Decision Processes and Reinforcement Learning, p18~21 をモデルにしています。

この様子を書き下すと、以下のようになります。

1. 確定報酬を設定する
2. 各状態sについて、実行可能なaにより得られる報酬を計算する

• $\gamma \sum T(s, a, s') U(s')$

1. 1の中で最も高い報酬が得られるaで、報酬総和$U(s)$を計算する

• $U(s) = R(s) + \gamma max \sum_{s'} T(s, a, s') U(s')$ = Bellman Equation!

1. 収束する($U(s)$の更新幅が少なくなるまで)まで1に戻り、更新を繰り返す

• 最終的には期待値へ収束することが証明されている

こうして、Value Iterationにより「環境のみから」報酬マップを推定することができました。ただ、この状態だとすべての状況に置けるすべての行動をしらみつぶしに調べていることになるので、最適な行動は導けますがあまり効率が良くありません。そのため、まず適当な戦略を決めてしまって、その範囲で報酬の探索を行い、更新していくという手法を考えます。それがPolicy Iterationです。

Policy Iteration

Policy Iterationでは、まず適当(ランダム)な戦略$\pi_0$を決めます。そうするとそこから「戦略から得られる報酬」$U^{\pi_0}(s)$が計算できるため、それを基に戦略を改善します($\pi_1$)。つまり、以下のようなステップになります。

1. 適当な戦略($\pi_0$)を決める
2. 戦略を元に$U^{\pi_t}(s)$を計算する
3. 戦略$\pi_t$を更新し$\pi_{t+1}$とする。($\pi_{t+1} = argmax_a \sum T(s, a, s') U^{\pi_t}(s')$)
4. 収束するまで1に戻り、更新を繰り返す

収束するとは$\pi_{t+1} \approx \pi_{t}$、つまり選択される行動がほぼ変わらなくなったら、となります。この繰り返しをPolicy Iterationと呼びます。

さて、Value IterationやPolicy Iterationにより、最適戦略を計算することはできそうです。しかし、式を見ればわかる通りこの計算には$T(s, a, s')$が判明している必要があります。つまり、各状況において行動した場合の遷移先が事前に明らかでないといけないということです。
これは微妙に大きい制約で、特に状況の数ととれる行動の数が多い場合、「ここでこうしたらこうなって・・・」と、すべからく設定するのはとても大変になります。

これを解決するのが、次節で紹介するQ-learningとなります。事前の環境(モデル)設定が不要なことから、"Model-Free"の学習方法とも呼ばれます。

Q-learning

では、Q-learningでは環境(モデル)の情報がない中でどうやって学習をするのでしょうか。その答えは「まず試してみる」となります。$T(s, a, s')$が不明でも、一回状態sで行動aをとってみればs'は明らかになるわけですから、この「試行」を繰り返すことで学習していくわけです。当然こんなことをしているとずいぶん時間がかかるので、そういう意味では事前のモデル設定が不要というメリットがある反面、学習時間の面でハンデを背負うことになります。

「まず試してみる」を定式化すると、以下のようになります。

$$
Q(s, a) \approx R(s, a) + \gamma max_{a'} E[Q(s', a')]
$$

$T(s, a, s')$が消え、期待値($E[Q(s', a')]$)となっています。試行を繰り返すことでこの期待値は精緻化されていきます。よって、最終的には上記でほぼ等しい($\approx$)となっている式は等式として成立するようになります。なぜなら、等式が成立するということは見込みの値($Q(s, a)$)と、実際行動した場合の期待値($R(s, a) + \gamma max_{a'} E[Q(s', a')]$)が等しいということであり、報酬の正確な見込みができているということになるためです。これが学習完了の目安になります。

この学習の過程を式にすると、以下のようになります。

$$
Q(s, a) = Q(s, a) + \alpha(\underline{R(s, a) + \gamma max_{a'} E[Q(s', a')]} - \underline{Q(s, a)})
$$

$\alpha$は学習率で、期待値($\approx$実際の報酬)と見込みの差分から学習をしていくということになります。この差分(=誤差)をTD誤差といい(TD = Temporal Difference)、TD誤差により学習を行う手法をTD学習といいます。つまり、Q-learningはTD学習の一種になります。

なお、上記の式は以下のようにもかけます。

$$
Q(s, a) = (1 - \alpha)\underline{Q(s, a)} + \alpha(\underline{R(s, a) + \gamma max_{a'} E[Q(s', a')]})
$$

少し複雑になってきましたが、これらはつまるところ「どの状態で、どう行動したら、どういう報酬が得られるのか」を明らかにしようとしているということです。この報酬の見込みの表をQ-Tableといいます(下図参照)。

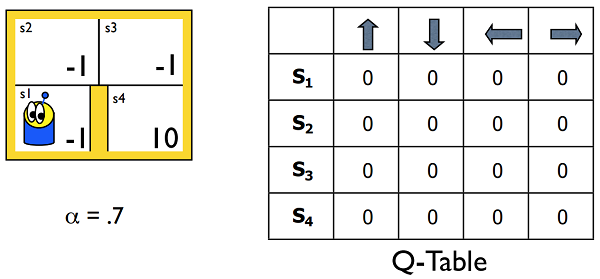
Markov Decision Processes and Reinforcement Learning, p39

上記資料のp39~p46にかけて、Q-Tableがどのように更新されていくのか、つまりどう学習が進んでいくのかを確認できるため、参考にしてみてください(資料中0.9となっているのは$\gamma$、報酬の割引率です)。

これで$Q(s, a)$をどんどん改善していけるようになりました・・・が、そもそもどうやってaを決めるのか、という問題がまだ残っています。端的には$Q(s, a)$が最大のものを選んでいけばいいのですが、これだと「わかっている中での最大」を選び続けることになるため、まだ未知の報酬の高い$s'$にたどり着ける可能性をつぶしてしまうことになります。
お宝があるかもしれない未知の道をとるか、報酬がわかっている安定した道をとるか・・・これはトレードオフの関係にあり、exploration and exploitation dilemma(探索/活用のジレンマ)と呼ばれます。

この問題に対するアプローチはいくつかありますが、基本的な手法としてε-greedy法があります。εの確率で冒険をして、あとはgreedy、つまりわかっている報酬を基に行動を行うという手法です。他にはBoltzmann分布($P(a|s) = \frac{e^{\frac{Q(s, a)}{k}}}{\sum_j e^{\frac{Q(s, a_j)}{k}}}$)を使った手法があり、これは$k$が大きいとランダム、小さくなるにつれわかっている中で報酬の高い行動をとるようになります。

これであとはひたすら戦略に基づき行動を繰り返し$Q(s, a)$を更新していけば、いつかは最適な値に収束することが証明されています。そう、いつかは・・・
しかしいつかを待てないのが人間なので、どうにかして最適な$Q(s, a)$を近似できないかと色々な試みが行われてきました。その中のうち、ニューラルネットワークを用いた近似が近年目覚ましい精度を出したDQN、Deep Q-learningへと繋がっています。

Deep Q-learning

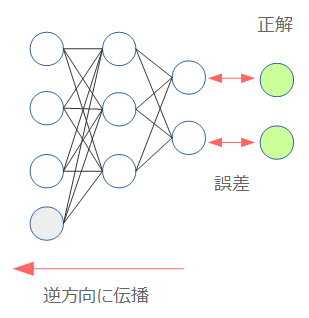
ニューラルネットワークの学習の基本は誤差伝搬法(Back Propagation)になります。端的に言えば、正解との誤差を計算して逆方向に伝搬させることで、モデルが正解に近くなるように調整する、という手法です。

Chainerで始めるニューラルネットワーク

そのため、ニューラルネットワークで$Q(s, a)$を近似する場合「誤差」はなんなのか、という点が問題になります。
ここで、上記で「TD誤差」という誤差が出てきました。

$$
Q(s, a) = Q(s, a) + \alpha(R(s, a) + \gamma max_{a'} E[Q(s', a')] - Q(s, a))
$$

これは報酬の期待値($\approx$実際の報酬)と、見込みの差分でした。これが誤差の定義のとっかかりになりそうです。
まず、$Q(s, a)$をニューラルネット化します。この時のニューラルネットの重みを$\theta$とし、$Q_\theta(s, a)$とします。そうすると、上記の式のTD誤差を利用した誤差の定義は以下のようにかけます。

$$
L_\theta = E[\frac{1}{2} (\underline{R(s, a) + \gamma max_{a'} Q_{\theta_{i-1}}(s', a')} - Q_\theta(s, a))^2]
$$

二乗しているのは誤差のためで、$\frac{1}{2}$しているのは微分したときに出てくる2を消すためです($f(x) = x^2$のとき、$f'(x) = 2x$)。式の構成から分かるとおり、下線部(期待値)が教師あり学習でいう所の教師ラベル(target)になります。
そして、この式を微分し得られる誤差伝搬する際の勾配は以下のようになります。

$$
\nabla_\theta L(\theta_i) = E[(\underline{R(s, a) + \gamma max Q_{\theta_{i-1}}(s', a')} - Q_{\theta_i}(s, a))\nabla_\theta Q_{\theta_i}(s, a)]
$$

これで準備は完了です。
ただ、勘の良い方はあれ？と思ったかもしれませんが、期待値側の$Q$が$Q_{\theta_{i-1}}(s', a')$になっています。これはひとつ前の$\theta$を使って期待値を計算するため、このようになっています。前述のとおりここは教師あり学習でいう所の教師ラベルの役目を果たしており、そのため期待値側の方は$\theta$が式に入っていますが勾配を計算する際ここは微分対象ではありません。この点は、実装する際注意しておく必要があります。

さてあとは学習するだけ・・・なんですが、実はこれこのまま学習してもなかなかうまくいきません。ニューラルネット化したことで余計にパラメーターが増えているわけですから当然と言えば当然でもありますが・・・。そのため、学習におけるいくつかの工夫が編み出されており、これを含んで初めてDeep Q-learningが可能になります。

Experience Replay

強化学習において与えられるデータは、当たり前ですが時系列的に連続したものになっています。これだとデータ間に相関が出てしまうので、なんとかばらばらにしたい、というのがExperience Replayが目指している所になります。

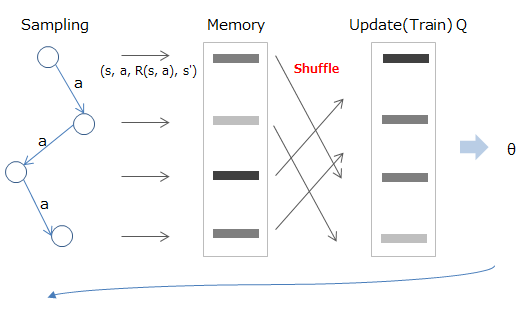
手法としては、まず一旦経験した状態/行動/報酬/遷移先をメモリーに蓄積し、学習を行う際はそこからランダムサンプリングして利用する、といった流れになります。

数式的には、以下のようにメモリー(D)の中に記憶した値からサンプリング行い(赤字部分)、計算済みの期待値(青字部分)を使って学習する、という感じになります。

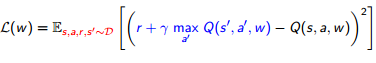
Deep Reinforcement Learning/David Silver, Google DeepMind, p12

Fixed Target Q-Network

期待値に含まれる$Q_{\theta_{i-1}}(s', a')$ですが、これは教師ラベルの役目を果たしているにもかかわらず、ひとつ前の重み$\theta_{i-1}$に依存しています。そのため、さっきまでAだったのに次はB、と$\theta$が更新されるにつれラベルが変わってしまいます。まさに朝令暮改的な状態です。

そのため、上記のExperience Replayのようにまずデータからいくつかサンプルを抽出してミニバッチを作成し、その学習中は期待値の計算に利用する$\theta$は固定する、とします。

数式的には、以下のように期待値の計算に使用する$w^-$(赤字)を固定することで、期待値(青字部分)を安定させる、ということです。学習が終わった後に$w^-$を$w$へ更新し、次回のバッチの計算に移ります。

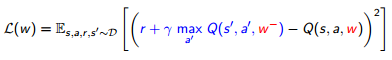
Deep Reinforcement Learning/David Silver, Google DeepMind, p13

報酬のclipping

これは与える報酬を固定するということで、正なら1、負なら-1という風に決めてしまいます。そのため報酬の重みづけ(速くゴールできたから10pt!のような)はできなくなるのですが、その代わりに学習が進みやすくなります。

以上のように、Deep Q-learningとはQ-learningをニューラルネットワークで近似するという手法と、その場合の学習を効率的に進めるための(少なくとも)上記3つのテクニックを包含したものになります。
ニューラルネットワークによる近似には、状態sの入力として数値ベクトルが受け取れるようになったというメリットもあります。ブロック崩しなどのゲームにおいて、ゲームの画面をそのままベクトル化して入力、学習させるといった芸当はこれにより可能になっており、AlphaGoでも同様の手法(盤面の画像をそのまま入力として使う)が使われています。

Deep Q-learningは現在進行形で様々な改良が行われていますが、上記の内容を把握していればそれらの研究動向を追う際の理解の助けになる、と思います。

実践

ここまでは理論的な内容でしたので、ここからは実際に試してみましょう。
強化学習用の様々な学習環境をまとめた、Open AIというプラットフォームがあります。今回は、こちらを利用し実際にアルゴリズムを学習させてみます。

OpenAI Gym
「AI用トレーニングジム」を、OpenAIがオープン

こちらを見ていただければわかるとおり、ゲームをはじめとして様々な学習環境が提供されています。見ているだけでも楽しいですね。

OpenAI Gym environments

こちらは実際にはPythonのライブラリとなっており、インストール方法は公式のGitHubに詳しい記載があります。

openai/gym

インストールは基本的にはpip install gymですが、これは最小構成のインストールで動かせるのは以下の環境のみです。

• algorithmic
• toy_text
• classic_control (描画にpygletが必要)

他の学習用環境では追加のインストールが必要です。例えば、Atariのゲームを動かす場合はpip install gym[atari]で追加のモジュールをインストールする必要があります。Python以外のインストールが必要場合もあるので、その際はInstalling everythingに記載のものを入れておけば間違いないです。Python3で使い場合は、Supported-systemsの記述に注意してください。

使い方は、Documentに記載の通りですが以下のような形になります。

import gym


env = gym.make('CartPole-v0')  # make your environment!

for i_episode in range(20):
    observation = env.reset()
    for t in range(100):
        env.render()  # render game screen
        action = env.action_space.sample()  # this is random action. replace here to your algorithm!
        observation, reward, done, info = env.step(action)  # get reward and next scene
        if done:
            print("Episode finished after {} timesteps".format(t+1))
            break

1. env.reset()で環境の初期化(ゲームのリセットに相当)
2. 観測された状態(state=observation)から、何らかのアルゴリズムでactionを決定
3. 'env.step(action)'により、行動に対する報酬(reward)と、行動により遷移した次の状態(state')を得る
   
4. doneはepisodeの終了を表す(勝負の結果がついた状態)。ここまでたどり着いたら、1に戻り再度学習を開始する

env.monitorを使えば、簡単に精度のモニタリングをしたりビデオを撮ったりできます。この結果はOpenAIのサイトにアップロードすることもできるので、われこそはという方は試してみましょう。

実際に実装してみたコードはこちらです。OpenAI Gymの方に結果をアップロードしているので、そちらで評価結果も確認できます(icoxfog417's algorithm)。

icoxfog417/chainer_pong

実装に際しては、以下のコードを参考にしました。

• ugo-nama-kun/DQN-chainer
• karpathy/pg-pong.py

なお、学習にはかなりの時間がかかり、そのため上手くいっているのかどうか判別するのにもかなり時間がかかります(上記のgistのコードの方は、学習に3日くらいかかってます)。画像認識もそうですが、端的に言えばGPUがないと開発は厳しいです。そういう意味では、昨今の機械学習では、サンプルを動かすだけでないのならGPUは必須になりつつあります。

とはいえ、AWSのGPUインスタンスなど手軽に環境は用意できるようになってきているので、ぜひ試してみてください(インスタンス立ち上げているときすごいドキドキしますが)。

解説は以上となります。ゼロからDeepまで潜っていただけたら幸いです！

参考文献

• Reinforcement Learning
• Machine Learning: Reinforcement Learning
• Markov Decision Processes and Reinforcement Learning
• Reinforcement Learning: A User’s Guide
• Value Iteration, Policy Iteration, and Q-Learning
• UC Berkeley CS188 Intro to AI Course Materials/Project 3: Reinforcement Learning
• Deep Q-learning
• DQNの生い立ち ＋ Deep Q-NetworkをChainerで書いた
• 最近のDQN
• Deep Q-Network　論文輪読会
• Artificial Intelligence: What is an intuitive explanation of how deep-Q networks (DQN) work?
• Deep-Q learning Pong with Tensorflow and PyGame
• Deep Reinforcement Learning: Pong from Pixels
• Deep Reinforcement Learning/David Silver, Google DeepMind