こんにちは。 DeepLearning で対話ロボットを作ろうとしているインコです。
この記事は mixi Advent Calendar 2017 の 12/03 の記事です。
概要
近年対話モデルとして DeepLearning を用いた End to End のアプローチが盛んに行われています。
この記事ではこれらに用いられるモデルとして一問一答に使われる Seq2Seq から出発して、複数発話コンテキストを扱いベイズ的なアプローチを組み込んだ VHRED を理解することをゴールとします。
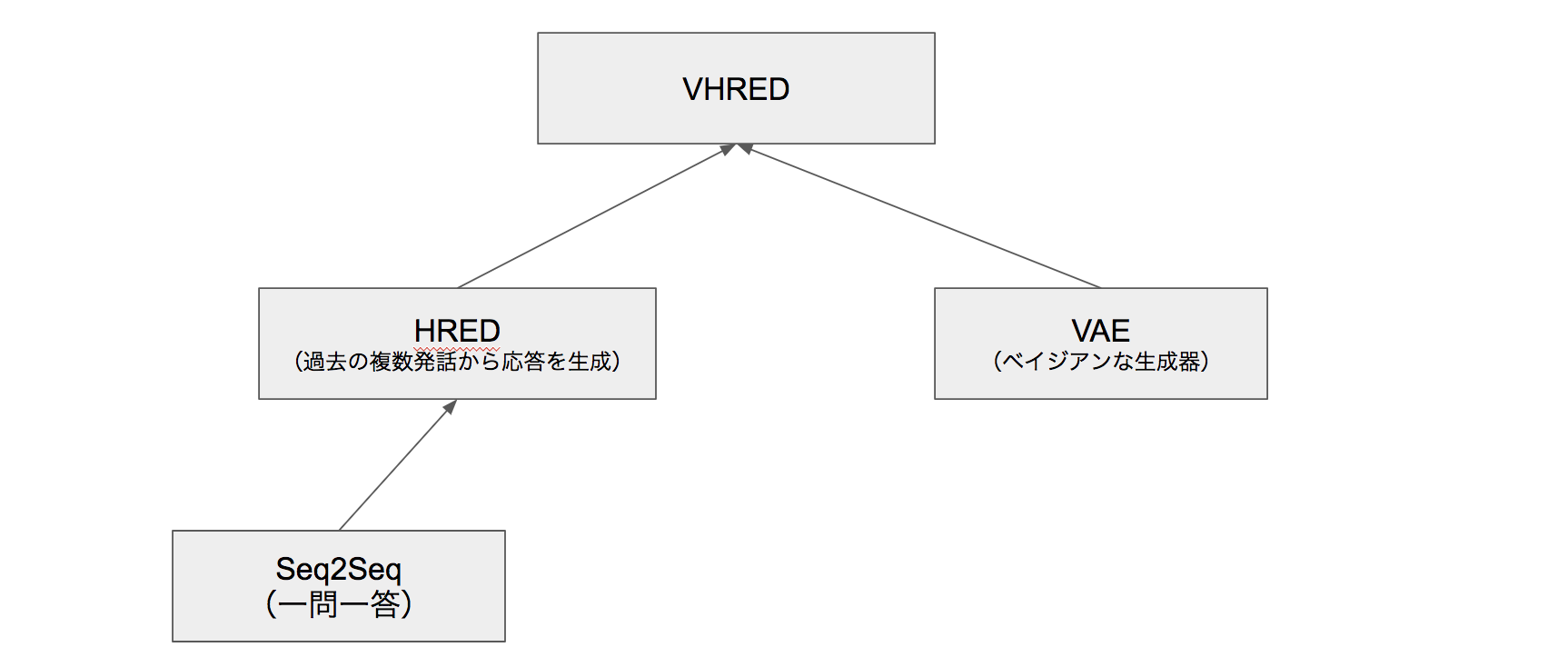
会話モデルのもろもろ
Seq2Seq
https://arxiv.org/pdf/1506.05869.pdf
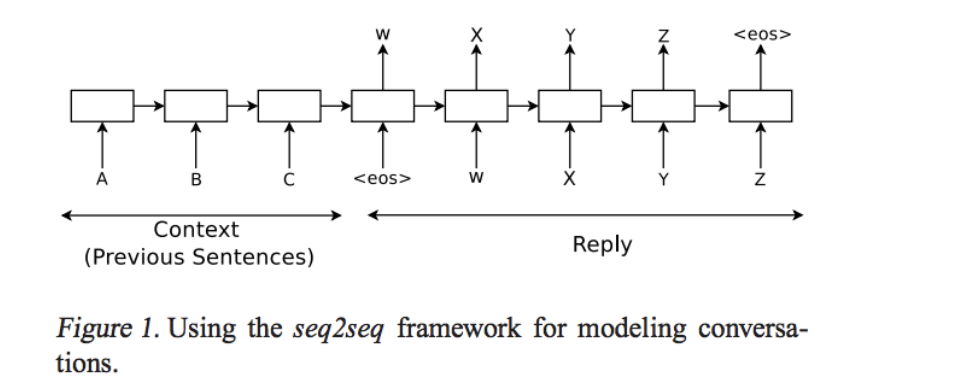
DeepLearning で対話!と言ったときにまず出てくる基本的なモデルが Sequence to Sequence こと Seq2Seq です。
これは発話・応答のシーケンスのペアを学習させることで、発話から応答を生成するモデルです。
tensorflow 上にも実装があります。
対話モデル以外にも様々な方面に応用されていますが、特に入力を日本語の文、出力を英語の文などとして翻訳モデルとして盛んに使われています。 Google 翻訳が 2016/11 に劇的に精度向上したのが話題になりましたが、この Google 翻訳にも Seq2Seq が使われているようです。
構造
LSTM などの RNN を用いたネットワークで2つの部分から構成されます
(LSTM?? RNN?? という方はLSTMネットワークの概要 を読むのがおすすめです)
- Encoder RNN: (図の Context) 人間からの問いかけの文章を単語などトークンに区切って渡します
- Decoder RNN: (図の Reply) システムからの応答を単語などトークン毎に生成します
Encoder RNN は図のトークン A, B, C を入力として受け取ったあとの final state を Decoder RNN の initial state として渡します。
この Encoder RNN の final state は thought vector と呼ばれており、 A, B, C という文章全体の情報を持つベクトルとなるとされています。
Seq2Seq をうまく学習させるための研究は盛んに行われており、 LSTM を多層にする、 Encoder RNN を bidirectional RNN にする、 Attention Mechanism (日本語解説) を使うなど様々な性能改善手法があります。
もうすこし具体的に
これだけだと抽象的でわかりづらいのでもう少し具体的なフローを説明します。
「インコは可愛いね」 という文を Seq2Seq に入力して、 「可愛いよね」 が生成されるまでの過程は以下のようになります。
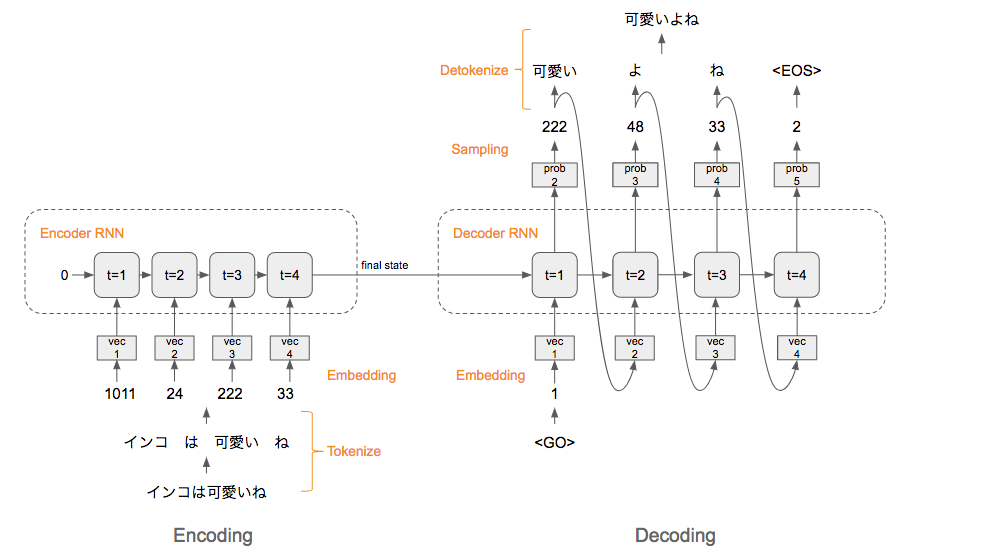
- Encoding
- Tokenize: 文章を単語等(token と呼びます)毎に分割し、 token 毎の ID に変換します。
-
Embedding: ID から、その token を表す分散表現ベクトルに変換します。
- Word2Vec が有名ですね。
- 私のチームではこれを文字単位で行う Char2Vec なども試しています。
- word2vec を使わなくとも、 token ID と一対一対応する適当な正規分布からサンプルしたベクトルを入れておけば OK です。
-
Encoder RNN: ベクトルを順番に RNN に入力していきます。
- vec1 を RNN に入力して hidden state (横矢印)を出力。この hidden state と次の入力 vec2 をまた RNN に入力してまた hidden state を出力・・を繰り返します。
- 最後の vec4 を入れたときの hidden state を final state としてとっておきます。
- この final state が thought vector と呼ばれ、「インコは可愛いね」という文の意味のようなものを表すベクトルとなっています。
- Encoder とはつまり、「インコ可愛いね」という文(の ID 列)を thought vector にエンコードするものなわけです
- Decoding
-
Decoder RNN: Encoder RNN の final state (thought vector) から、各 token の生成確率を出力していきます
- final state を Decoder RNN の initial state ととして設定し、特別なシンボル
<GO>の Embedding を入力 - RNN の隠れ層に全結合層等を噛まして、 token ID ごとの生成確率を出力。
- 例えば
[0.1, 0.001, 0.3, ..]なら ID:0 は10%、ID:1は0.1%・・といった具合
- 例えば
- final state を Decoder RNN の initial state ととして設定し、特別なシンボル
-
Sampling: 生成確率にもとづいて token をランダムに選びます
- より精度の良い生成を行うにはここでビームサーチを行います
-
Embedding: 2で選ばれた token を Embedding して Decoder RNN
への次の入力とします。 - Detokenize: 1-3 を繰り返し、2で得られた token を文字列に直します
-
Decoder RNN: Encoder RNN の final state (thought vector) から、各 token の生成確率を出力していきます
このようにして、 Seq2Seq はインコの可愛さに同意することが可能になります。
ここで最終的に説明したい VHRED への伏線として、 2.2 で次の**token (単語等)**を選ぶときに(重み付き)ランダムサンプリングをしていることを覚えておいて下さい。
ニューラルネットというとランダム性無く決定論的に生成を行うイメージがありますが、 Seq2Seq ではこのように単語などの並びというレベルでは生成される文にランダム性をもたせることができます。
できること
元論文では映画のセリフを学習データとして使うことで以下のように様々な問に答えるモデルができたとしています。
Human: who is skywalker ?
Machine: he is a hero .
Human: who is bill clinton ?
Machine: he ’s a billionaire .
Human: is sky blue or black ?
Machine: blue .
Human: does a cat have a tail ?
Machine: yes .
Human: does a cat have a wing ?
Machine: no
Human: can a cat fly ?
Machine: no .
...
ただし、このモデルは直前の会話のみを Encoder RNN に渡す仕組みですので、それより前の発言から次の発言を生成することはできません。つまり一問一答です。
HRED
https://arxiv.org/pdf/1507.04808.pdf
実装: https://github.com/julianser/hed-dlg-truncated
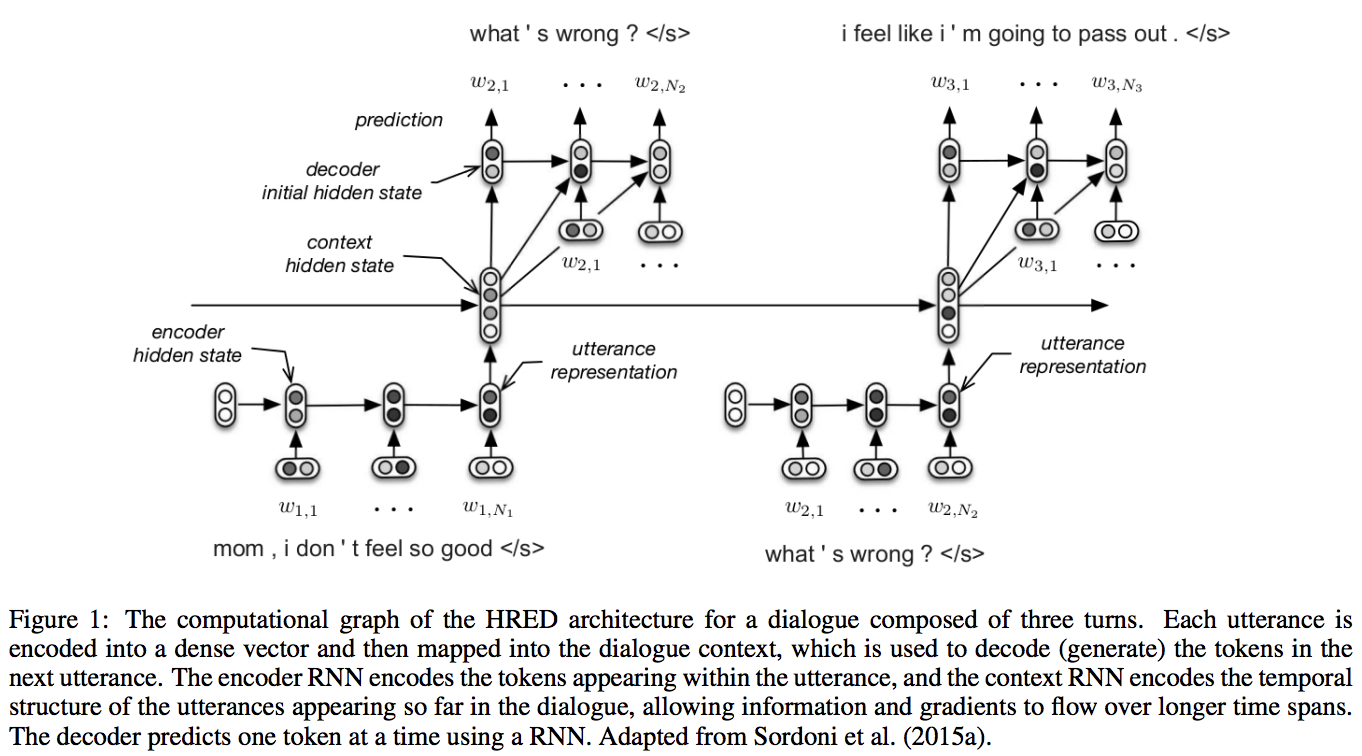
Hierarchical Recurrent Encoder-Decoder の略です。
Seq2Seq は一問一答ですが、これを過去の n-1 個の発話から次の n 個目の発話を推測するようにしたのが HRED です。
Seq2Seq では例えば
- システム:「インコ好きだよね?」
- ユーザー:「うん」
- システム:<次の答え>
の次の答えが「うん」のみから生成されるため、おそらくインコに関する話題が次生成されることはありません。
HRED では過去 n-1 個の発話から次の発話を生成するため、例えば「インコかわいいよねわかる。」みたいな発話を生成できる可能性があります。
構造
Seq2Seq は Encoder RNN, Decoder RNN の2段構成でしたが、 HRED は Encoder RNN, Context RNN, Decoder RNN の3段構成です。
- Encoder RNN: 一つ一つの文章(会話なら過去の一つ一つの発言)をそれを表すベクトルに変換する
- Context RNN: Encoder のまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する
- Decoder RNN: Context RNN の情報から応答を生成する
2 の Context RNN というレイヤーがあることによって、過去の発話の履歴を加味した返答をできるようになっているということですね。
VAE
VAE は対話モデルではないのですが、最終的に説明をしたい VHRED を数学的に理解する上で重要なモデルですので説明をします。
https://arxiv.org/pdf/1312.6114.pdf
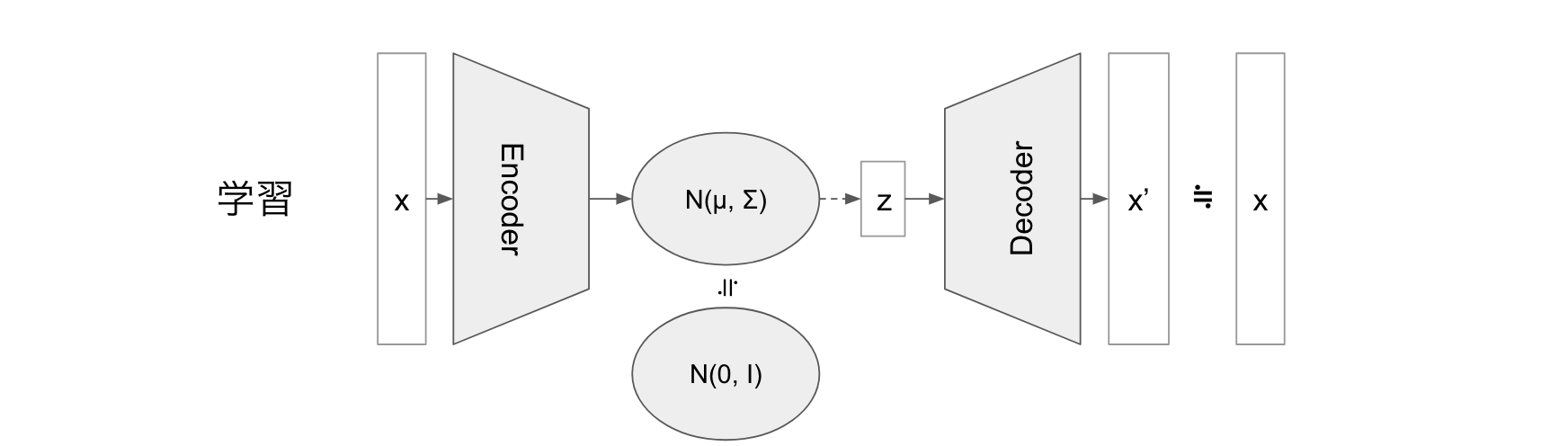
標準正規分布からサンプリングした潜在変数 z から画像等データを生成することのできるモデルです。
Variational Autoencoder徹底解説 がとても詳しくわかりやすく書かれておりおすすめです。
VAE ができること
標準正規分布 $\mathscr{N}(0, I)$ から適当な潜在変数 z をサンプリングして VAE に入力することで、学習データをうまく補完したようなデータを生成できます。
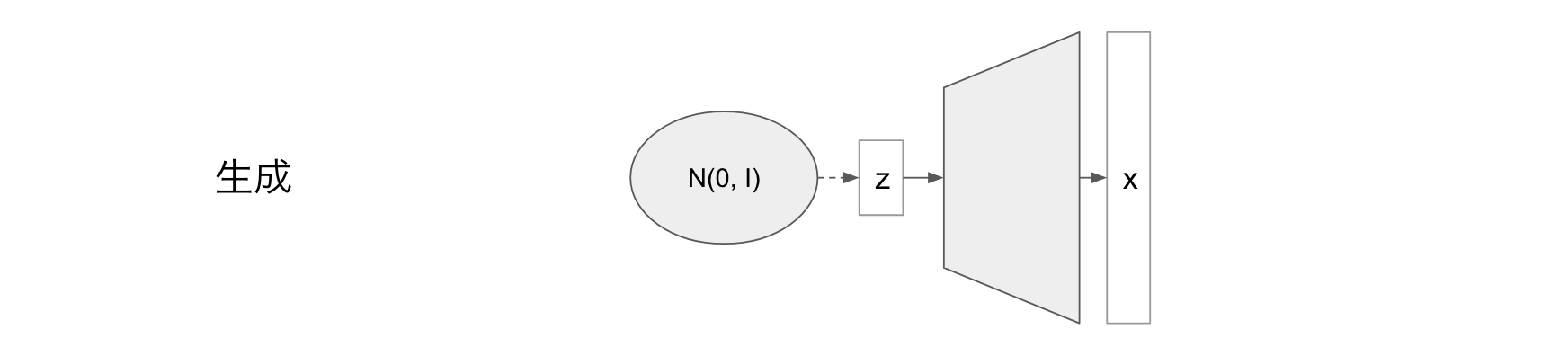
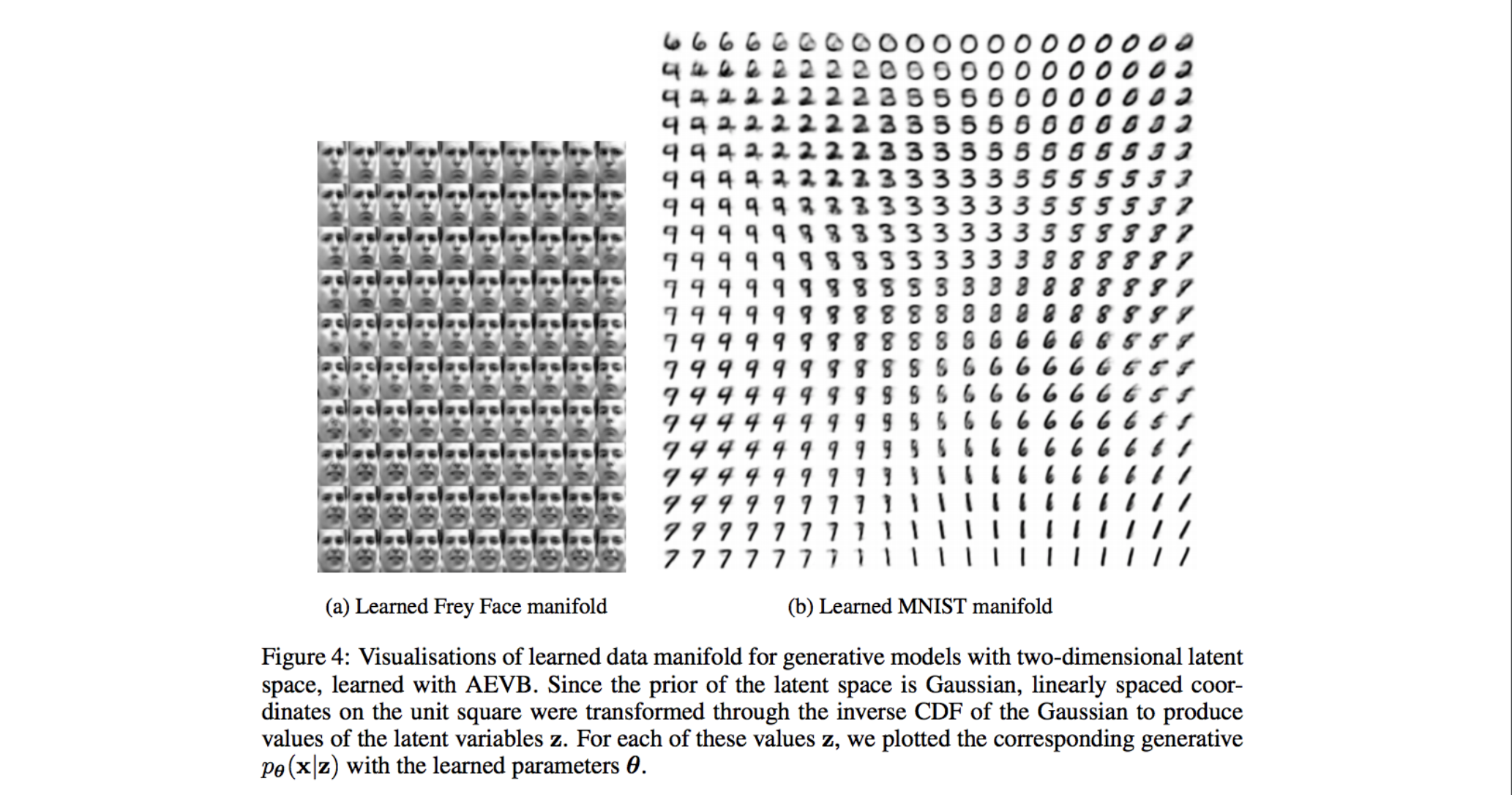
この例では画像を生成していますが、言語の生成への応用なども研究されています。
VAE の数学的な考え方
Auto-Encoding Variational Bayes で提案された、潜在変数
z からデータ x が生成される場合の汎用な数学的モデルがまずあり、 VAE はその例として書かれているものです。
Auto-Encoding Variational Bayes
まずは VAE の元になっている数学的モデルの説明をします。
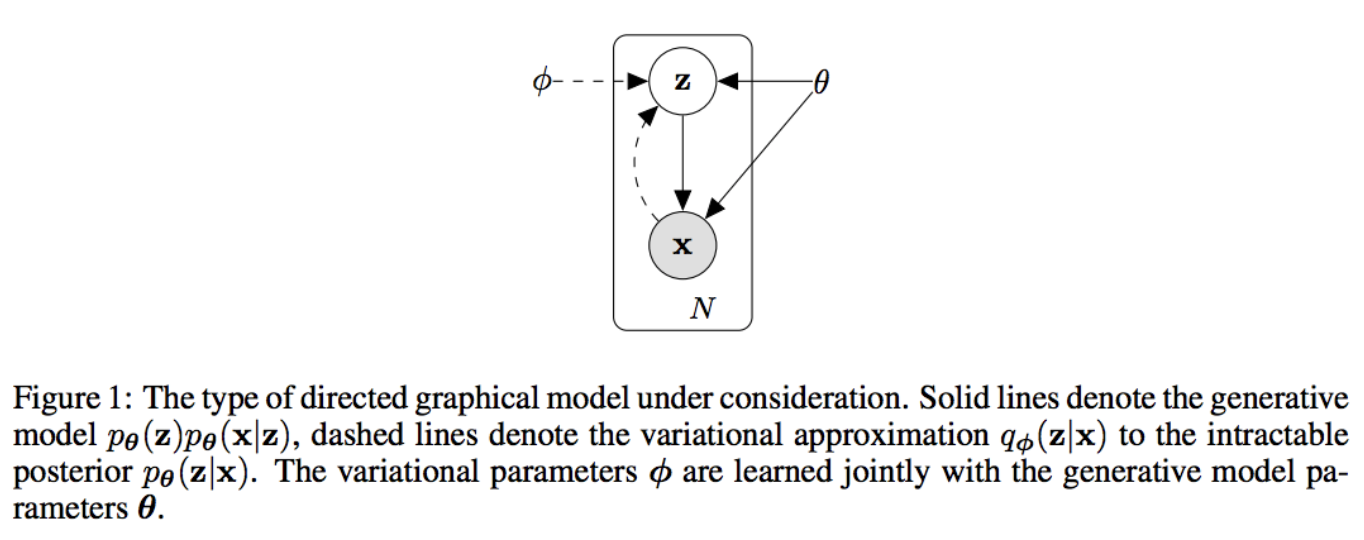
潜在変数 z の事前分布 $P_\theta(z)$ があり、 $P_\theta(x|z)$ によって x が生成されるとします。
この時点では $P_\theta(z)$, $P_\theta(x|z)$ はその確率密度関数が $\theta, z$ 両方に関してほぼ全体で微分可能という仮定はありますが、とくにそれらが正規分布だとかいう仮定はありません。
このようなモデルでの対数尤度を最大化することを考えます。
L=\sum_xlogP_\theta(x)
目的は上の対数尤度 L を最大化する $\theta$ を見つけることになります。
L を最大化するには各 $logP_\theta(x)$ を最大化すれば良いです。
付録1、 Lower Bound の導出より、適当な分布 $Q_\phi(z|x)$ に対して以下が言えます。
logP_\theta(x) \geqq -KL[Q_\phi(z|x)||P_\theta(z)] + E_{Q_\phi(z|x)}[logP_\theta(x|z)]
- $Q_\phi(z|x)$ は事後分布 $P_\theta(z|x)$ の近似(付録1参照)
- $KL[Q||P]$: Kullback-Leibler divergence つまり Q, P 2つの分布の差異。非負。
- $E_Q(P)$: 確率分布QでのPの期待値。
この右辺を Lower Bound と呼び、この右辺を最大化することによって $logP_\theta$ を最大化します。
つまり、 KL を小さくして E を大きくすれば良いわけです。
VAE
ここで、 P, Q の条件付き確率に対して、条件を入力としてその確率分布を出力するニューラルネットワークを使うことを考えます。
これが VAE です。
VAE では $P_\theta(z)$ は標準正規分布 $\mathscr{N}(0,I)$ を仮定します。
- $Q_\phi(z|x)$: Encoder
- x を入力として z の分布を出力
- VAE では正規分布を仮定
- $\mathscr{N}(\mu(x), \sigma(x))$ の $\mu, \sigma$ を出力するニューラルネット
- x を入力として z の分布を出力
- $logP_\theta(x|z)$: Decoder
- z を入力として x の分布を出力
- VAE では正規分布もしくはベルヌーイ分布を仮定
- z を入力として x の分布を出力
右辺第一項の $KL[Q_\phi(z|x)||P_\theta(z)]$ は Encoder をできるだけ $P_\theta(z)$ に近づければ小さくなります。
$P_\theta(z)$ は標準正規分布としたので、 $logP_\theta(x)$ を大きくするには $Q_\phi(z|x)$ (Encoder) を標準正規分布に近づくよう学習させればよいことになります。
右辺第二項の $E_{Q_\phi(z|x)}[logP_\theta(x|z)]$ は $x$ を Encoder への入力として $z$ を生成し、その $z$ を更に Decoder に入力して $x^\prime$ を出力するニューラルネットとみなせます。ですのでこの出力 $x^\prime$ が真の分布に近づくよう、大元の入力 $x$ との誤差を小さくするよう学習させることで $logP_\theta(x)$ を大きくできます。
VHRED
https://arxiv.org/pdf/1605.06069.pdf
実装: https://github.com/julianser/hed-dlg-truncated
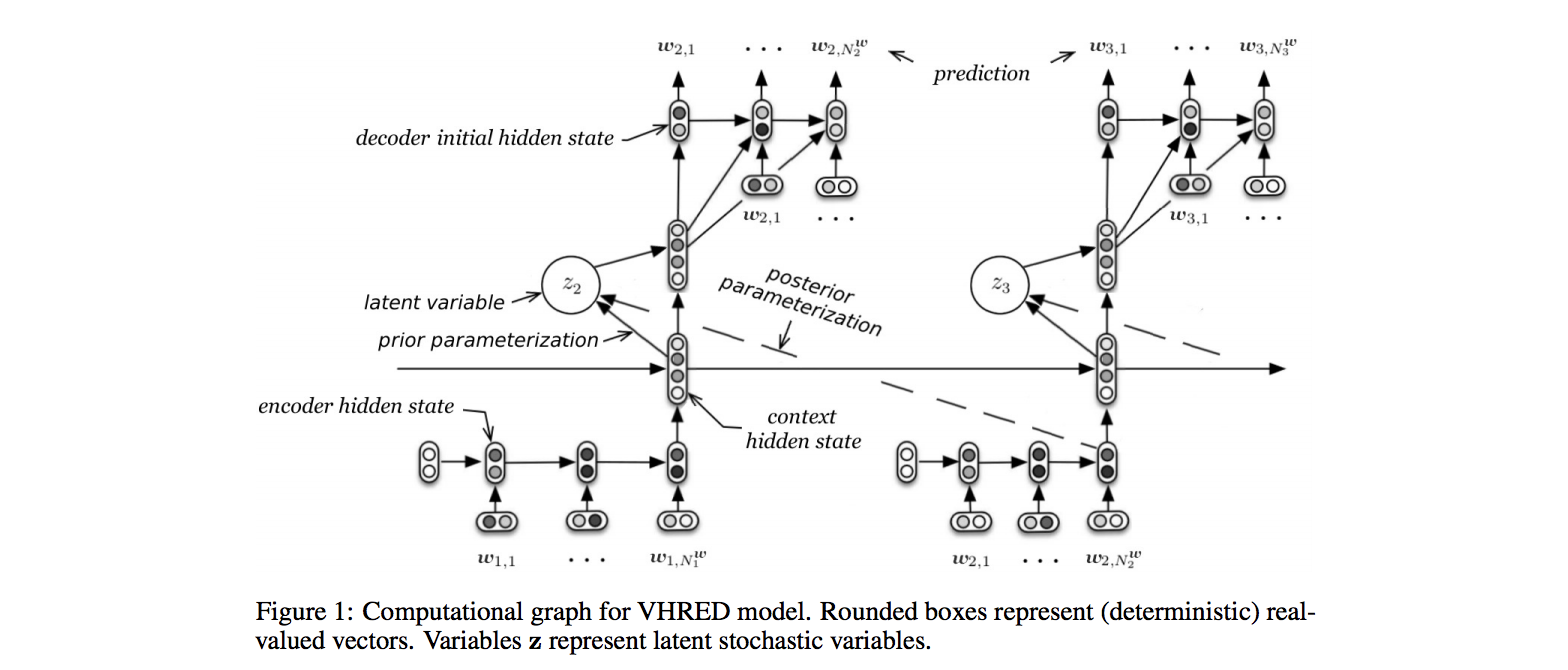
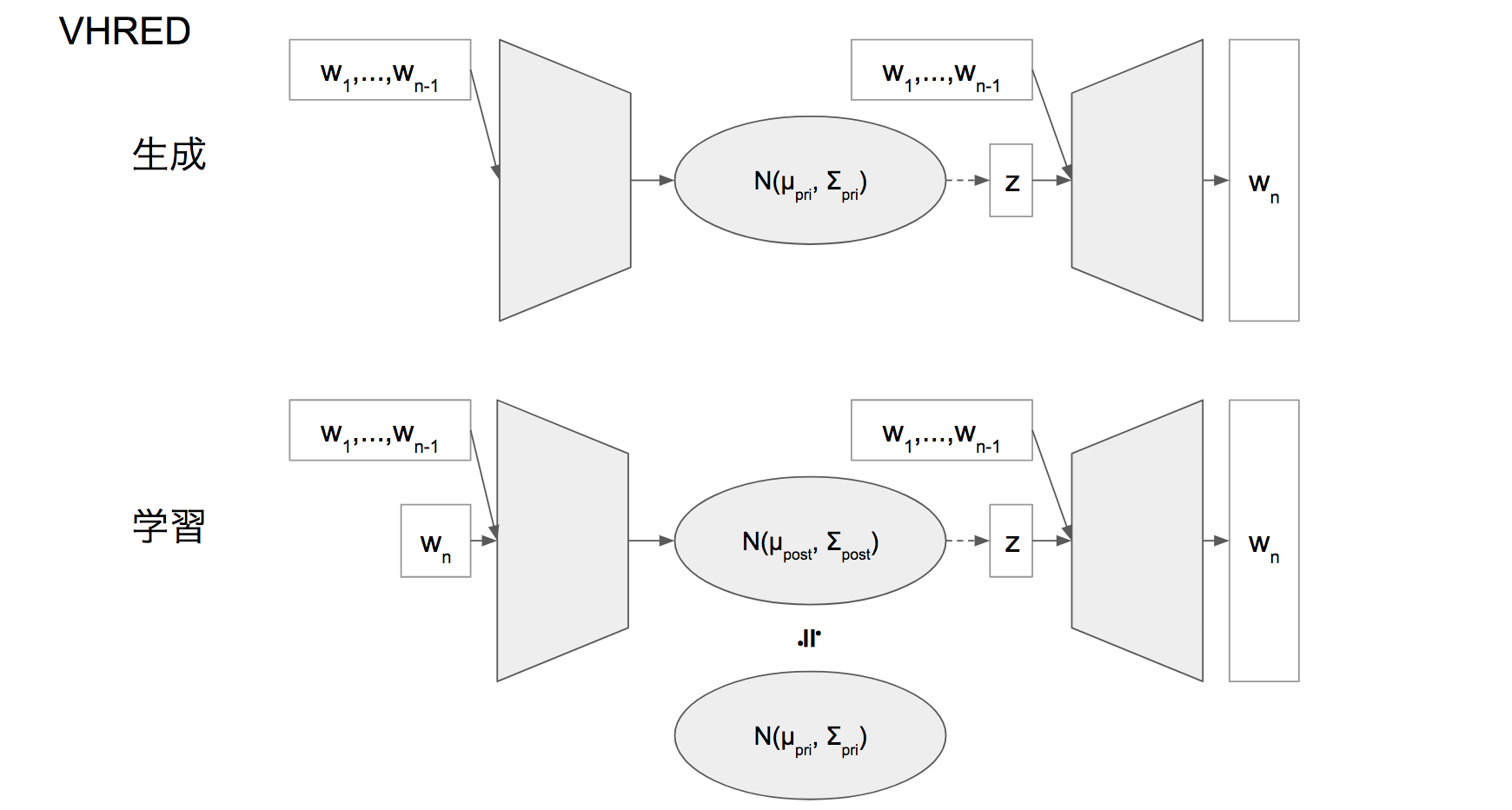
上のネットワーク図を見て分かる通り、 HRED に対して VAE の潜在変数 z を組み合わせたモデルです。
VHRED でできること
HRED と同じく過去の n-1 個の発話を与えられて、 n 個目の発話を生成します。
ただし、 HRED は対話学習において以下の問題を持っておりこれを解決することを目的にしています
- HRED は確率的な多様性が字面にしかなく、会話の「流れ」のようなロングタームな多様性が無い。
- Encoder RNN, Context RNN, Decoder RNN のうち確率的な処理が Decoder RNN の次ステップの単語を生成する部分にしか無いから。
- これによって、同じコンテキスト(発話リスト)を与えられても、答えの内容が毎回会話の流れとしては同じものしか出せない。
- HRED は短く情報量に乏しい答えをしがちである。
- 同じコンテキスト(発話リスト)を与えられても、それに続く発話は全く異なるものでありうる
- 「おはよう」「やあおはよう」 というコンテキストに対し 「いい天気だね」 も 「昨日の件どうなった?」も会話として成立する
- これらを決定論的に学習しようとすると、結果「無難な」答えつまり短いよくある答えを学ぶ傾向がある。
- 「うん」「そうだね」「・・・」など。
- 同じコンテキスト(発話リスト)を与えられても、それに続く発話は全く異なるものでありうる
これに対し、 VHRED では Context RNN の部分に確率的なノイズを与えて学習することで上記の問題を解決します。
- VHRED は会話の流れを表す Context RNN にノイズを乗せることで、同じコンテキストに対しても字面だけではない多様な返答ができる
- VHRED はコンテキストに対する返答のばらつきを Context RNN の確率的な幅で吸収することでそれらをうまく学習できる
特に論文では VHRED では HRED などの従来の会話モデルに比べより長い文章を生成する傾向があることが書かれています。
VHREDの数式的な理解
VHRED は HRED に VAE の潜在変数の概念を追加したものとみなせますが、 HRED 側から入るよりも VAE 側から数式的に理解していくほうが近道です。論文の数式を VAE と比較しながら読み解いていきます。
VHRED は、 $w_i$ で表される、 i 番目の発話が i=1, ..., n-1 まで並んだ状態での、 $w_n$ の発話について考える問題となっています。
ここで n は現在の発話の数で、一つの会話全体で N 個の発話があるとします。
各発話 $w_i$ は各単語等トークン $w_{i,1}, ..., w_{i,m}$ から成っているとします。
例えば、「おなかが減った」「そろそろ行く?」「ラーメンがいいな」という文章であれば
- $w_1$: おなかが減った
- $w_{1,1}$: おなか
- $w_{1,2}$: が
- ...
- $w_2$: そろそろ行く?
- ...
などとなります。
VHRED では $logP_\theta(w_1, ..., w_N)$ を観測された w のセットに対し最大化しようとします。
潜在変数 z の分布
VAE では z は標準正規分布 $\mathscr{N}(0, I)$ に従いますが、 VHRED では $z_n$ 以下の $\mu_{prior}, \sigma_{prior}$ という関数によって平均と分散が決まる正規分布に従うとされます。
(付録1の VAE の式変形上は Q は必ずしも標準正規分布である必要は無いですね。)
P_\theta(z_n|w_1, ..., w_{n-1}) = \mathscr{N}(\mu_{prior}(w_1, ..., w_{n-1}), \sigma_{prior}(w_1, ..., w_{n-1}))\\
添字が n-1 までで n は含まれないのがキーポイントになってきます。
尤度 logP を最大化する
VAE と同じく Lower Bound が求められそれを最大化します。
logP_\theta(w_1, ..., w_N) \geqq \sum_{n=1}^N\left\{ -KL[Q_\phi(z_n|w_1, ..., w_n)||P_\theta(z_n|w_1, ..., w_{n-1})] + E_{Q_\phi(z_n|w_1, ..., w_n)}[logP_\theta(w_n|z_n, w_1, ..., w_{n-1})] \right\}
この式を注意深く見てみると、添字が $n$ の部分と $n-1$ の部分が入り混じっています。実はこの数式の $w_{n-1}$ と $w_n$ の間にはとても大きな溝があります。
VAE での $logP_\theta$ は
logP_\theta(x) \geqq -KL[Q_\phi(z|x)||P_\theta(z)] + E_{Q_\phi(z|x)}[logP_\theta(x|z)]
でしたが、ここで
- $z$ -> $z_n$
- $x$ -> $w_n$
として、各確率に条件 $|w_1, ..., w_{n-1}$ をつけてnを1~Nまで和をとると VHRED の式になることがわかります。(付録2)
VHRED の式で $w_n$ を $x$ としてみるとわかりやすいかもしれません。
logP_\theta(w_1, ..., w_N) \geqq \sum_{n=1}^N\left\{ -KL[Q_\phi(z_n|x, w_1, ...,w_{n-1})||P_\theta(z_n|w_1, ..., w_{n-1})] + E_{Q_\phi(z_n|x, w_1, ..., w_{n-1})}[logP_\theta(x|z_n, w_1, ..., w_{n-1})] \right\}
つまり VHRED は数式的には、
- $w_1, ..., w_{n-1}$ が事前に与えられている状態での
- $w_n$ と $z_n$ での VAE
と見ることができます。
VAE では $Q_\phi(z|x)$ は $\mathscr{N}(\mu(x), \sigma(x))$ であるとされましたが、 VHRED では $\mathscr{N}(\mu_{posterior}(w_1, ..., w_n), \sigma_{posterior}(w_1, ..., w_n))$ とします。
(上に出てきた prior の方は $w_1, ..., w_{n-1}$ のみなのに対して、この posterior は $w_n$ も入っていますね。)
VAE で $Q_\phi(z|x)$ の $\mu, \sigma$ を $P_\theta(z) = \mathscr{N}(0,I)$ つまり0, I に近づけたように、 VHRED では $\mu_{posterior}, \sigma_{posterior}$ を $\mu_{prior}, \sigma_{prior}$ に近づけるよう学習を行います。
VHRED がやろうとしていること:数式的な方向から
生成も学習も、 $w_1, ..., w_{n-1}$ によって条件付けされた状態での潜在変数 $z_n$ の学習と、その $z_n$ からの $w_n$ つまり発話生成を行っていると考えられます。
- 学習
- $w_1, ..., w_{n-1}$ によって条件付けされた状態で
- $w_n$ を入力として(潜在変数 $z_n$ を介して) $w_n$ を出力する学習
- $z_n$ も $w_1, ..., w_{n-1}$ によって条件付けされたある正規分布に従うよう正則化がされる
- 生成
- $w_1, ..., w_{n-1}$ によって条件付けされた状態で
- $z_n$ をサンプリングし
- (VAE の文脈での)Decoder で $w_n$ を生成する
VHRED のニューラルネット的な理解

再び VHRED のモデル図です。
先程の数式的な方面からの理解により、なぜ学習時に posterior parametarization つまり今生成しようとしている次の発話 $w_n$ が入力になってるんだ?とかが理解できると思います。
先程の数式とネットワークが以下のように対応します
- $|w_1, ..., w_{n-1}$ の条件: n-1 までのデータを Encoder RNN と Context RNN に入力したときの Context RNN の final state
- $w_n$:
- エンコード時: n のデータでの Encoder RNN
- デコード時: Decoder RNN の出力
- $Q_\phi(z_n|w_n, w_1, ..., w_{n-1})$: Context RNN と Encoder RNN の final state を FNN に食わせたもの
- 出力は $\mu_{posterior}, \sigma_{posterior}$
- $P_\theta(w_n|z_n, w_1, ..., w_{n-1})$: Decoder RNN
- 入力
- $\mu_{posterior}, \sigma_{posterior}$ からサンプリングされた z
- Context RNN の final state
- 入力
Github のコードでのネットワーク
本家の Github に上がっているコードをざっと見た感じ以下のようなネットワークになっているようです。
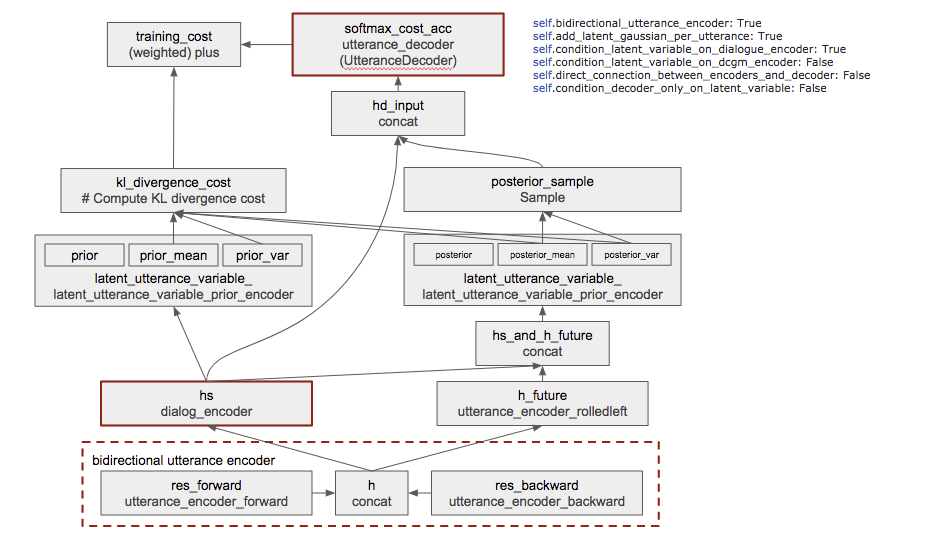
- ボックス: 処理とその返り値の変数名
- 一行目: 返り値の変数名
- 二行目: その処理をおこなう関数など
- 太い茶色枠は HRED にもある要素
- プログラムは設定によって様々な構成の NN を作れるよう書かれているので、図では図右上の条件でのものを書いています
- 一部省略した部分などもあります
おわりに
最初は VHRED 論文の自身での整理とチームメンバーへの共有の目的で書き始めたこの記事ですが、途中から Advent Calendar に出そうという気持ちになり、 Deep Learning の対話モデルの話にしようと風呂敷を広げ続けた結果、このような長大な文章になってしまったことをお詫びいたします。
DeepLearning といえば画像!ということで画像・CNN から Deep Learning に入った方は多いと思いますが、自然言語処理、とくに言語の生成に興味を持ってくれる Deep Learner が増えたらいいなと思っています。
私自身大学時代にロボットの視覚と運動指令を結びつけるモデルとして RNN は使っていたものの、今のチームに移動してから初めて自然言語処理で Deep Learning をはじめた人です。
ロボットを動かすのにせよ、画像を生成するのにせよ、自然言語を生成するのにせよ、何かを生成できるモデルというのはとてもおもしろいです。何か生き物のようなものを感じます。
この面白さに触れられる人が増えますように。
付録
付録0. よく使う式変形・定義
a. 確率の積分
\int_zP(z)dz = 1
b. 期待値
確率密度関数 $Q(z)$ に対し値 $X(z)$ の期待値
E_{Q(z)}[X(z)] = \int_zX(z)Q(z)dz
c. ベイズの定理
P(x,z) = P(z|x)P(x)
d. Kullback-Leibler divergence
カルバックライブラー情報量。2つの分布 P, Q の差。非負。
KL[P(z)||Q(z)] = \int_z P(z)log\left\{\frac{P(z)}{Q(z)}\right\}dz
付録1. VAE Lower Bound の導出
$logP_\theta(x)$ に対し任意の分布 Q を組み込んで KL の式が出るように変形していくことで下限(Lower Bound)を求めます。
なぜそんな式変形を・・となりますがパターンです。
logP_\theta(x) = \int_zQ_\phi(z|x)logP(x)dz
~~ \verb|←a. より追加された部分は1|\\
= \int_zQ_\phi(z|x)log\left\{\frac{P_\theta(x,z)}{P_\theta(z|x)}\right\}dz
~~ \verb|←c. ベイズの定理|\\
= \int_zQ_\phi(z|x)log\left\{\frac{Q_\phi(z|x)}{P_\theta(z|x)}\frac{P_\theta(x,z)}{Q_\phi(z|x)}\right\}dz
~~ \verb|←分子分母にQをかけた|\\
= \int_zQ_\phi(z|x)log\left\{\frac{Q_\phi(z|x)}{P_\theta(z|x)}\right\}dz
+ \int_zQ_\phi(z|x)log\left\{\frac{P_\theta(x,z)}{Q_\phi(z|x)}\right\}dz\\
= KL[Q_\phi(z|x)||P_\theta(z|x)] + \int_zQ_\phi(z|x)log\left\{\frac{P_\theta(x,z)}{Q_\phi(z|x)}\right\}dz
~~ \verb|↑d. 左辺は KL|\\
\geqq \int_zQ_\phi(z|x)log\left\{\frac{P_\theta(x,z)}{Q_\phi(z|x)}\right\}dz
~~ \verb|← KL は非負(≧0)|
まとめると、この右辺を $L_b$ として以下の不等式が成り立ちます。
logP_\theta(x) \geqq L_b \\
\left(L_b = \int_zQ_\phi(z|x)log\left\{\frac{P_\theta(x,z)}{Q_\phi(z|x)}\right\}dz \right)
ちなみに上に出てきた $KL[Q_\phi(z|x)||P_\theta(z|x)]$ は、事後確率 $Q_\phi(z|x), P_\theta(z|x)$ が近いほど0に近づきます。
$L_b$ を大きくしようとすると上記の KL は小さくなるので、 Q は P に近づいていきます。すなわち $Q_\phi(z|x)$ は $P_\theta(z|x)$ の近似とみなせます。
次にこの $L_b$ が KL と期待値となることを示します。
L_b = \int_zQ_\phi(z|x)log\left\{\frac{P_\theta(x,z)}{Q_\phi(z|x)}\right\}dz \\
= \int_zQ_\phi(z|x)log\left\{\frac{P_\theta(z)}{Q_\phi(z|x)}P_\theta(x|z)\right\}dz
~~ \verb|← c. ベイズの定理|\\
= - \int_zQ_\phi(z|x)log\left\{\frac{Q_\phi(z|x)}{P_\theta(z)}\right\}dz
+ \int_zQ_\phi(z|x)logP_\theta(x|z)dz\\
= -KL[Q_\phi(z|x)||P_\theta(z)] + E_{Q_\phi(z|x)}[logP_\theta(x|z)]
~~ \verb|←d. KL と b. 期待値|
これらをまとめて、
logP_\theta(x) \geqq -KL[Q_\phi(z|x)||P_\theta(z)] + E_{Q_\phi(z|x)}[logP_\theta(x|z)]
付録2. VHRED Lower Bound の導出
logP_\theta(w_1, ..., w_N) = \sum_{n=1}^NlogP_\theta(w_n|w_1, ..., w_{n-1})
あとは
logP_\theta(w_n|w_1, ..., w_{n-1})
に対して、 VAE の式を
- $z$ -> $z_n$
- $x$ -> $w_n$
として、各確率に条件 $|w_1, ..., w_{n-1}$ をつけて全く同じ計算をするだけです。