概要
シーケンス(例えば文章)のペアを関連付けて学習させる DeepLearning の手法 sequence-to-sequence learning において、長いシーケンスでの学習の精度を上げると言われている Attention Mechanism の論文を読んだので備忘録を兼ねて概要を書いておきます。
元論文: Neural Machine Translation By Jointly Learning To Align And Translate
そもそも seq2seq とは
シーケンスのペアを大量に学習させることで、片方のシーケンスからもう一方を生成するモデルです。
元論文: Sequence to Sequence Learning with Neural Networks
tensorflow 上にも実装があります。
実用例としては以下のようなものがあります。
- 翻訳: 英語 -> フランス語 のペアを学習。英語を入力するとフランス語に翻訳してくれる。
- 構文解析: 英語 -> 構文木 のペアを学習。英語を入力すると構文木を返してくれる。
- 会話bot: 問いかけ -> 返答 のペアを学習。「お腹減った」に対して「ご飯行こうぜ」などと返してくれる。
いろいろ夢の広がるモデルです。
LSTM を使った以下のような形をしたネットワークで、入力を内部表現に変換するエンコーダ部分(画像左半分)と内部表現から出力を得るデコーダ(画像右半分)で構成されます。

引用元:TensorFlow
このネットワークの動きを英語->日本語翻訳を例に考えていきます。
このネットワークは、エンコーダ部で入力された単語列を基にネットワークの隠れ状態(図の四角い箱)を更新していき、入力文の「意味」のようなものを図の <go> の上の四角に対応する隠れ状態に詰め込みます。go の上の四角には I have a pen の、意味のような英語でも日本語でもないもやっとしたものが入っているわけです。そして右半分ではその「意味のようなもの」を表す内部状態から、日本語の文章を生成していきます。「私はペンを持っている」が出力されるわけです。
seq2seq の問題点と Attention Mechanism のやりたいこと
seq2seq の問題は長い文章への対応が難しいことです。具体的には上の例での「意味のようなもの」を表すのが固定次元のベクトルであることに問題があります。つまり、3単語のとても短い文であっても、50単語あるとても長い文であっても、その意味をある固定次元ベクトルの中に押し込まなくてはなりません。
そこで、文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていくような何らかの仕組みが必要になります。
Attention Mechanism ではこの問題に対して、「入力と出力のどの単語が関連しているのか」を学習させることで対応します。
下図のようにネットワークは翻訳前後の単語の対応関係を学習し、単語列の出力時に対応する入力の単語を引っ張ってくることで長い文書でも翻訳の精度をあげます。
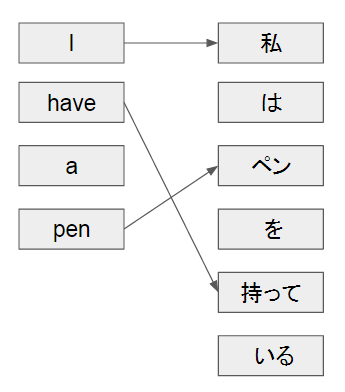
(上の図では理解を助けるため余分な線は引いていません)
これによって従来より長い文章でも翻訳の精度が上がったということが書かれています。
Attention Mechanism の原理
以下上記をどのように実装しているのかを図と数式で説明します。
ネットワークと変数の説明
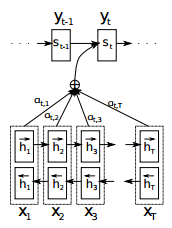
引用元:Neural Machine Translation By Jointly Learning To Align And Translate
- 入力側
- $x_j$: j番目の入力単語
- $h_j$: j番目の入力に対応する隠れ層
- 入力側はバイディレクショナル RNN になっており、隠れ層には順方向のものと逆方向のものがあります。それぞれ矢印の向きで表現されています。
- 出力側
- $y_t$: t番目の出力単語
- $s_t$: t番目の出力単語に対応する隠れ層
- AttentionMechanism
- $\alpha_{ij}$: i番目の単語に対してj番目の単語が関連している確率もしくは結びつきの強さ
各ニューロンの値の決定のされ方
出力側から遡って、どのようにi番目の出力とj番目の入力が関連づくのか見ていきます。
出力の隠れ層の決定
出力の隠れ層、 $s_i$ は次のように決定されます。
$$s_i = f(s_{i-1}, y_{i-1}, c_{i})$$
$s_{i-1}, y_{i-1}$ の部分は普通の RNN です。ここででてくる $c_i$ が以下で述べるように、 i番目の出力に関連度が高い入力の隠れ層の値になる ように学習されるというのがミソです。
関連する入力の決定
では $c_i$ がどのように決定されるのか見ていきましょう。
$$c_i = \sum_{j=1}^{T_x}\alpha_{ij}h_j$$
$h_j$ はj番目の入力の隠れ層の値です。 $\alpha_{ij}$ は上に出てきたように、i番目の出力に対してj番目の入力が関連している確率になるよう学習されます。そして下で説明するように $\alpha_{ij}$ はただ1つのjに対して大きい値(≒1.0)を持ち、他はほぼ0になるよう学習されます。すなわち、 $c_i$ はi番目の出力に関連度が高い入力の隠れ層になるわけです。i番目の出力に関連が高い入力が $j_{max}$ 番目とすると以下のようになります。
$$c_i = \dots ≒ h_{j_{max}}$$
入力の関連度の高さの確率の決定
では $\alpha_{ij}$ がどのように決定されるのか見ていきましょう。
$$\alpha_{ij} = \frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})} = softmax_j(e_{ij})$$
ここで $softmax_j$ は j に関する softmax 関数で、 $e_{ij}$ の内 j に関して一番でかいものだけがほぼ1.0をとり、他はほぼ0になるような関数です。名前の通り max をとっているようなものですね。
では $e_{ij}$ はなんなのだというと、
$$e_{ij} = a(s_{i-1},h_j)$$
とされており、 a はこの seq2seq モデル全体とともに学習されるフィードフォワードニューラルネットワーク(FNN)と書かれています。
まとめると
時刻iの出力の隠れ状態 $s_i$ を計算するときに以下のような処理がはしります。
FNN によって、前時刻の出力の内部状態 $s_{i-1}$ 及び各時刻jの入力 $h_j$ を入力として、時刻iの出力に最も関連のありそうな入力時刻 j が計算されます($e_{ij}, \alpha_{ij}$)。そして、その時刻の入力の隠れ層が $c_i$ として $s_i$ への入力の一部になります。
これを図で表すと、

引用元:Neural Machine Translation By Jointly Learning To Align And Translate
のようになります。
ちなみに論文にはエンコーダ部分をバイディレクショナル RNN にするという話もあるのですが本記事ではそこは割愛します。