物理ベースレンダリングを柔らかく説明してみる（５）

今回は光の単位について

　今まで４回(第１回、第２回、第３回、第４回)に渡って、「柔らかく」「ゆるふわ」に物理ベースレンダリングの解説を試みてきたこのシリーズですが、さすがにいつまでも避けて通るわけにはいかない話題もあります。それは光の単位についてです。今回は多分、あんまり柔らかくないと思いますがご了承ください。
　アーティストさん向けの「具体的にどうやってPBRアセットを作ればいいの？」という疑問や「IBL（イメージベースドライティング）やUnreal EngineやUnityなどに通ずる実際的なPBRの実装の基礎」などについては、また次回以降にやりたいと思います。

光の単位は二種類！？　「放射量」と「測光量」とは

　まず、光の単位といってもいろいろあるのですが、今日ではそれらは大きく２種類に大別されます。その種類とは「放射量（ほうしゃりょう）」と「測光量（そっこうりょう）」です。

　前者の「放射量」は、光を純粋なエネルギーとして捉えた時の光量の測り方・単位になります。光はエネルギーの一つです。エネルギーとはなんでしょうか。物理的な定義はおそらくWikipediaや物の本に載っているかと思うのですが、少なくともエネルギーを何らかの対象に働きかけることで「仕事」をするものとここでは考えましょう。物理を高校で習ったことのある方は「J（ジュール）」や「W（ワット）」というエネルギーの単位について勉強された経験があると思います。光のエネルギーは、実はこれらの単位で表すことができます。¹
　仕事、とかいいましたが、CG的にはそのエネルギー量での光が人間の目に感知されることで、人間の知覚に明るさとして認識されます。そのエネルギー量が大きいほど、人に知覚される「光の明るさ」も大きくなります。

　一方の「測光量」とはなんでしょうか。これは、光の放射（放射量）を人間の眼が受けて、それを人間が実際に感じる「明るさ」の量になります。なんだか、こう聞くと曖昧に聞こえますね。例を出しましょう。現在のディスプレイはRGBという光の３原色、つまり赤・緑・青の光の量のバランスで色を表現しています。HTMLやお絵かきソフトで、RGB値をそれぞれ（255, 0, 0）（つまり赤原色）と(0, 0, 255)（つまり青原色）の２つ作ってみてください。２つを「明るさ」を見比べてみましょう。
　・・・（255, 0, 0）（赤原色）の方が、ずっと明るく見えないでしょうか？　これは、人間の目の仕組みとして、「光の波長によって感じる光の明るさに差がある」という性質によるものです。この波長によって異なる「明るさ」についての感度を「分光視感効率」といいます。^{2 3 4}
　測光量をもう少し具体的に言えば、光の放射（放射量）を波長ごとに標準的な人間の目の分光視感効率で重みを付け合計した光の量ということができます。これは、実際に計算して算出することができる光の量であり、定義によると波長 555 nmの単色光の放射束が 1 ワット [ W ] あったときの光束は 683 ルーメン [ lm ] であるとされています（ワットやルーメンについては後述）。

　ちなみに、放射量は物理量（エネルギーとして直接計測できるので）といえますが、測光量は人間の知覚に基づく単位なので厳密には物理量ではなく、心理物理量と呼ばれます。

放射量単位の幾何学的な分類

　光の単位は放射量と測光量に大別できると書きましたが、それらはさらに幾何学的により細かく分類することができます。（今、若干読者の抵抗を感じましたが、むしろ今までは前座でこれからが本番です）

　以下Wikipediaからの実質的なコピペになってしまいますが、主に幾何学的に下表のように分類されます。（放射照度と放射発散度は、単位的には同じで、前者は特に入射光について、後者は特に出射光についての呼び方です）。

放射量	SI単位	記号	備考
放射エネルギー(Radiant energy)	ジュール	J	測光量における光度エネルギーに相当
放射束(Radiant flux)	ワット	W	測光量における光束に相当
放射強度(Radiant Intensity)	ワット毎ステラジアン	$\frac{W}{sr}$	測光量における光度に相当
放射輝度(Radiance)	ワット毎ステラジアン毎平方メートル	$\frac{W}{sr \cdot m^2}$	測光量における輝度に相当
放射照度(Irradiance)	ワット毎平方メートル	$\frac{W}{m^2}$	測光量における照度に相当
放射発散度(Radiosity)	ワット毎平方メートル	$\frac{W}{m^2}$	測光量における光束発散度に相当

（放射発散度(Radiosity)のラジオシティは、あのレンダリング手法の一つである、ラジオシティ法のラジオシティですね）

測光量単位の幾何学的な分類

　測光量についても、幾何学的な観点から複数に分類することができます。とはいえ、その分類は放射量と同じ対応関係として定義されています。なので、覚えるのは割と簡単です。
　こちらもWikipediaからのコピペですが、主に幾何学的に下表のように分類されます。（照度と光束発散度は、単位的には同じで、前者は特に入射光について、後者は特に出射光についての呼び方です）。

測光量	SI単位	記号	備考
光度エネルギー(Luminous energy)	ルーメン·秒	lm·s	放射量における放射エネルギーに相当
光束(Luminous flux)	ルーメン（またはカンデラ·ステラジアン）	lm	放射量における放射束に相当
光度(Luminous intensity)	カンデラ	cd	放射量における放射強度に相当
輝度(Luminouce)	カンデラ毎平方メートル	$\frac{cd}{m^2}$	放射量における放射輝度に相当
照度(Illuminance)	ルクス（またはルーメン毎平方メートル）	lx	放射量における放射照度に相当
光束発散度(Luminous exitance, luminous emittance)	ラドルクス（またはルーメン毎平方メートル）	rlx	放射量における放射発散度に相当

　ちなみに、放射量について「放射輝度」のつもりだけど「放射」を略して「輝度」と言ったり、「放射照度」のつもりだけど同様に省略して「照度」と言ったり書いたりしてしまう場合もよくあるので、文脈に注意が必要です。むしろ、英語でラディアンスやイラディアンス、ルミナンス、イルミナンス、と読んだほうが誤解が少ないかもしれません。

　さて、放射量と測光量、前者は物理量で、もう片方はそれ元に人間の分光感度を考慮して算出した心理物理量という若干の差はあれど、CGのライティング計算においては、むしろ両者に通じて存在する、「幾何学的な単位の各小分類をきちんと意識できるかどうか」、がより重要になってきます。そのため、今後の説明で片方についてのみ言及があったとしても、大抵はもう一方についても同様に言えることだと解釈してください。

放射エネルギー(Radiant energy)

　放射エネルギー、上の放射量の単位表の一番上の単位ですね。光は発光体や反射体から放たれ、他の領域へと注ぎ込まれていくわけですが、放射エネルギーとはその純粋な光のエネルギーそのものを指す物理量になります。単位はJ（ジュール）であり、わかりやすく言えば別の種類のエネルギーですが、J（ジュール）という単位自体のイメージとしては、熱エネルギーなどが想像しやすいかもしれません。とにかく、光もエネルギーの一種であり、物理量としては一番基本的な単位の１つであるJ（ジュール）で測られます。
　これに対応する測光量は光度エネルギー(Luminous energy)と呼ばれ、そちらの単位はlm·s（ルーメン・秒）になります。光度エネルギーの方はあまりCGでは意識しないかもしれません。物理量である放射エネルギーも、CGの光の単位の勉強で座学の最初に出てくるお約束のようなものです。

　多分、後述する放射束・光束などと違い、かけた時間次第でエネルギー量がどんどん変わってしまうため、共通の尺度としては扱いづらいことがあるのでしょう。後述の放射束・光束は、「共通の単位時間（秒）の間だけ測定したエネルギー量！」とぴっちり決まっているため、同じ基準で定量的に扱える（比較したり、計算に使える）わけです。

放射束(Radiant flux)

　CGで主に重要になってくる単位はここからです。放射束とは、一言で言うと「ある領域を単位時間あたりに通過する光のエネルギー」のことであり、その単位はW（ワット）です。Wは電気エネルギーの単位「電力」としても有名ですね。W（ワット）別の単位の呼び方でいうとJ/s（ジュール／秒）であり、つまりは時間当たりのエネルギーということになります。

放射束 \Phi = \frac{dQ}{dt}

　

　これに対応する測光量は光束(Luminous flux)で、単位はlm(ルーメン)です。なんか聞いたことありますね。LED電球や壁に映像を写すプロジェクターの光の明るさを表すスペック値の単位としても有名です。具体例をあげると、小型のプロジェクターで3000ルーメンあたりから、大型・高級機のプロジェクターだと5000〜7000ルーメンくらいでしょうか。

　他の幾何学的な光量単位を導出するにあたって基本となる単位になりますので、基本事項として覚えておいてください。

放射強度(Radiant intensity)

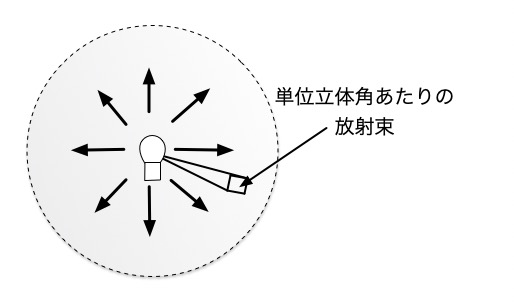
　放射強度は、「ある三次元的な角度（単位立体角sr：単位はステラジアン）単位における放射束」のことを意味します。この放射強度は登場頻度でいうと、後述する放射輝度（Radiance）や放射照度(Irradiance)ほど多くはありませんが、関連する単位として心の隅にとどめておきましょう。
　ちなみに測光量としては、光度といって単位はcm（カンデラ）、こちらはルーメンと同様に光学製品の照明性能のスペック値として使われることがよくあります。ただし、実際は光度（カンデラ）を直接的に正確に測ることはどうやら難しいようで、ルーメン（光束）や計測したルクス（照度）から逆算した値を載せていることが多いようです。

放射輝度（Radiance）

　（概念図を描くの難易度高くて断念しました。すみません…。）

　放射輝度は、単位射影面積あたりかつ単位立体角（sr:ステラジアン）あたりの放射束です。なかなかむづかしいと感じられるかもしれませんが、感覚的に捉えるならば、「方向性を強く意識した光量単位」と言えます。
　細かい話ですが、「単位面積あたり」ではなく、「単位射影面積あたり」とあるのがミソというか実際ややこしいところで、放射輝度の定義を式にすると以下のようになります。

L(x,\omega') = \frac{d^2 \Phi}{dA (\vec n \cdot \vec \omega') d \vec \omega}

　ちなみに、放射輝度の光が物体表面に垂直に入射している場合、この垂直入射であることを特に強調するために垂直放射輝度$L_\perp(x)$と表記することがあります。

　ライティング計算に放射輝度を用いる場合は、BRDFとコサイン項を放射輝度に乗算し、さらにそれを半球面上に積分する必要があります。これは計算としては非常に重く、重点（インポータンス）サンプリングなどの高速化手法を用いることが定石となっています。

　大雑把な話ですが、GPUなどでのリアルタイムレンダリングではなく、レイトレーシング法で計算する場合は特にこの放射輝度（または輝度）を意識することが多いと思います。

　ちなみに測光量である輝度の単位は$cd/m^2$（カンデラ／平方メートル）なのですが、言いにくいので別にnit（ニト）という単位の呼ばれ方をすることもあります。よく液晶ディスプレイの明るさを表すときに使われます。一般的な液晶ディスプレイの最大輝度は400nit程度。最近の４K HDRディスプレイの高級品などでは1000nitあたりまで出せる機種も出てきました。

放射照度（Irradiance）

　放射照度は、単位面積あたりの放射束です。より具体的に言えば「物体表面に流入する放射束を、単位面積あたりに換算した場合の放射量」ということになります。放射輝度が単位立体角という「向きの概念を持つ光の単位」とするなら、放射照度は「向きの概念を持たない光の単位」と言えます。
　放射輝度$L(x,\omega')$の入射光を半円球上に積分すると、その結果の量は単位としては放射照度$E(x)$になります。ただし、その積分の際には、放射輝度にコサイン項を乗算する必要があります。というのも、放射輝度は放射照度とは異なり「単位射影面積あたり」であるので、その互換を取るためです。

E(x) = \int_\Omega L_i(x,\omega')(\vec n \cdot \vec \omega')d \vec \omega'

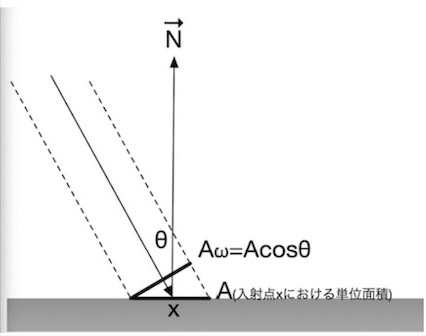
　言い換えると、放射照度は放射輝度と異なり、光が物体表面について垂直に入射してきた場合での測り方を前提としています。そのため、放射照度の算出にあたり、光が斜めから入射する可能性を想定し、垂直に入射してきた場合に換算するためにコサイン項を乗算して計算するわけです。
　ちなみに、平行光源や太陽光などの場合、それらが垂直に物体表面に入射した場合での放射照度を、垂直放射照度$E_\perp(x)$と表示することがあります。それらが実際に斜めに入射してきた場合、$E_\perp(x)$にコサイン項を乗算して、物体表面での放射照度$E(x)$を計算します。

　測光量である照度についても、心理物理量という特性を除けば、考え方は同様です。単位はルクスです。よく部屋の明るさなどを表す際に使われます。ちなみに一般的な部屋の明るさは３００〜８００ルクス程度といわれています。

　放射照度は出射光（反射光）を求める際に、単にBRDFに乗算するだけでよいため、ライティング計算は非常に楽です⁵。リアルタイムCGにおいては、扱う光源の入射光の光の単位が放射照度（または照度）であることが大半です。多くの方は、そこらへんを今まであまり意識せずにやっていたかもしれませんが、実はそうだったのです。⁶

各種光源にそれぞれ向いた単位はなに？

放射輝度と放射照度、それぞれのライティング計算について

　さて、以前の回でも説明したとおり、反射計算においては、物体の反射材質の数学的表現としてBRDFが関係してきます。
　その計算方法は主に２つあります。一つは入射光の単位が放射輝度または輝度の場合で、この場合は半球面上での積分計算が必要になります。

L_r(x, \vec \omega) = \int_\Omega f_r(x, \vec \omega', \vec \omega)(\vec n \cdot \vec \omega') L_i(x, \vec \omega') d \vec \omega'.

　上記はいわゆるレンダリング方程式です（エミッション項を省略していますが）。

　さて、この計算の放射照度または照度版があります。こちらは、なんと積分計算が必要ありません。非常に計算は楽ですね。⁵

L_r(x) = f_r(x,\vec\omega', \vec\omega) E(x).
ただし、
E(x) = E_\perp(\vec n \cdot \vec \omega')

$E_\perp(x)$は物体表面に対して、光源から放たれた光の（垂直に入射してきたときの）放射照度または照度です。実際は斜めに入射してくる場合も想定して、コサイン項を乗算して$E(x)$とします。

　この２パターンが、どうしてこういう計算になるのかについてはBRDFの定義とともに後述します。

点光源（ポイントライト）またはスポットライト

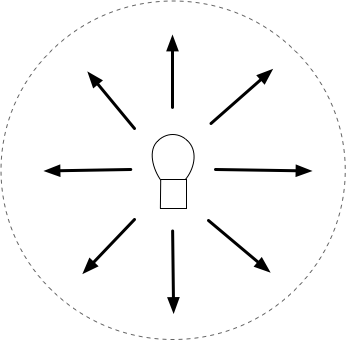
　点光源（ポイントライト）やスポットライトといった、仮想的なライト（なぜ仮想的かというと、実際の光源には表面積や体積がありますが、これらは幾何学的に無限小の点だからです）ですが、これらは放射状に広がるその性質から、放射束または光束の単位で扱うのが都合が良いようです。

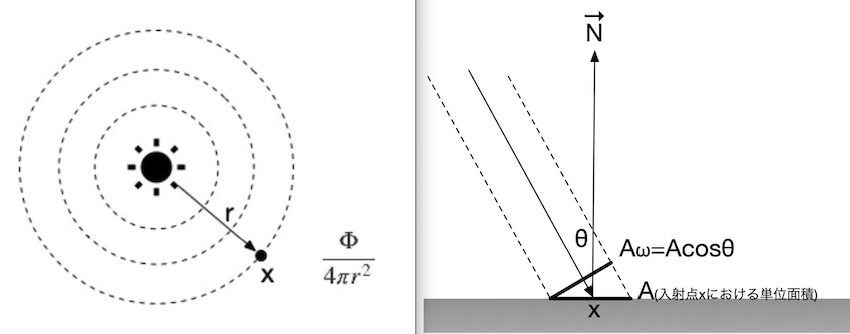
　理由としては、第１回でも書きましたが、点光源を例に取ると、光源中心から距離ｒ離れた地点での単位面積上の明るさ（放射照度または照度）は以下の図および式で考えられます。

光源からrの距離離れた物体の単位面積上の放射照度E(x) = \frac{\Phi (\vec n \cdot \vec \omega')}{4 \pi r^2}

（点光源から放たれた光は、物体表面の真上にある場合を除き、大抵は斜めに入射してくるでしょう。そのため、物体表面上の垂直方向の入射として放射照度に換算するためコサイン項$(\vec n \cdot \vec \omega')$の乗算が必要です）

　ここでよく考えてみてください。距離rは、実際のCGのケースによって様々ありえるわけで、放射照度を単位としてしまうと、その値は実際の放たれた光の到達位置によってバラバラになってしまいます。そんなの、CGソフトの光量プロパティとして利用するわけにはいきませんね。しかし、分子部分の放射束または光束を光量の単位として利用すれば、距離がいくら変わろうとも不変なので、定量的に取り扱いやすいというわけです。

また、ポイントライトとスポットライトにおいては、

放射束と放射強度の関係（放射強度を球面で積分すると放射束になる）から、

\Phi = \int_{\Omega} I dl = \int_{0}^{2\pi} \int_{0}^{\pi} I d\theta d\phi = 4 \pi I \\

放射束を$4 \pi$で割ると放射強度になります。

I = \frac{\Phi}{4 \pi}

すると、ポイントライトやスポットライトにおいては、物体表面における放射照度は実は下式のように、光源から放たれた光の放射輝度にコサイン項をかけることでも得られることがわかります（ただし、その放射輝度は上式に従い正しく算出されていることが前提です）

（以前、この記事では「放射輝度にコサイン項をかけて放射照度とするのは間違い」と書いていたのですが、いろいろ私の理解不足でした。それは文脈次第です。もちろんコサイン項をただかけるだけで単位が変化してしまうわけではもちろんなく、下式のように、点光源から光が放射状に広がる過程によって、結果的に式にするとそういう形に落ち着くのです。⁶

E = \frac{\Phi (\vec n \cdot \vec \omega')}{4 \pi r^2} = \frac{I}{r^2} (\vec n \cdot \vec \omega') = L_{in} (\vec n \cdot \vec \omega')

上式の２つめの等式については、放射強度の単位が$\frac{W}{sr}$、放射輝度の単位が$\frac{W}{sr \cdot m^2}$であったことを思い出しましょう。

平行光源（ディレクショナルライト）または太陽光

　平行光源（ディレクショナルライト）や太陽光（実際は完全な平行光源ではありませんが、地球とは非常に距離が離れているので平行光源とみなしてしまいます）場合、その明るさは放射照度または照度の単位で扱うほうが都合が良いようです。
　というのも、点光源やスポットライトと違って、平行光源は光のレイが並行に進む（広がらない）ため、少なくとも幾何学的な理由による減衰が起こらないからです（現実世界においては、大気の散乱現象などによる減衰はありえますが…）。つまり、放射照度または照度をそのまま光源の光量単位として使用できます。
　ただし、光源から発する光と、照射される表面で、同じ放射照度という単位同士ではありますが、やはり光が斜めに入射する場合を想定して、コサイン項を乗算します。

E(x) = E_\perp (\vec n \cdot \vec \omega')

（ここで$E_\perp$は平行光源から放たれる光が垂直に照射された場合の放射照度、$E(x)$は物体表面xに照射される放射照度です）

HDRI画像またはスカイライトによるIBL（イメージベースドライティング）

　これらの場合は、本質的には放射輝度または輝度を単位として使います。というのも、これらを使ってのレンダリングは、本質的には半球面上における積分計算だからです。つまり、例の以下の式です。

L_r(x, \vec \omega) = \int_\Omega f_r(x, \vec \omega', \vec \omega)(\vec n \cdot \vec \omega') L_i(x, \vec \omega') d \vec \omega'.

　ただし、実際にオフラインのレイトレーシングならともかく（オフラインでも、通常はインポータンスサンプリングという高速化手法を使って積分を行います。）、リアルタイムで半球面積分は、計算コストから言ってそうそう気楽にできるものではありません。
　余談になりますが、そのためリアルタイムCGにおけるHDRI画像のライティング利用では、HDRI画像の放射輝度（または輝度を）前もって積分したHDRI画像に変換する（これをHDRI画像のプレフィルタリング処理といいます）処理をよく行います（そうして変換された画像は、ぱっと見の印象ではぼやけた画像に見えます）。
　この変換後のHDRI画像を環境マップとして使い、シェーダー上でフェッチしてきた光量は、放射照度として扱います（積分済みだからです）。つまり、計算がラクな以下の計算にできるわけですね（※ディフューズIBLの場合のみ）⁵

L_r(x) = f_r(x,\vec \omega',\vec \omega) E(x).
ただし、
E(x) = E_\perp(\vec n \cdot \vec \omega')

　という工夫もあるとはいえ、まぁ本質的にはIBLにおける単位は放射輝度または輝度だと思ってください。

具体的な事例

　さて、ここまで読んで、一部のCG業務経験がある方は、もしかして……と思われたかもしれません。そうです。平行光源と点光源・スポットライト、IBLは、慣例的な単位が違うため、そのCGソフトまたはゲームエンジン上での光の強さの数値を直接比べることができません。

　たとえば、Unreal Engineのドキュメントを見てみましょう。点光源の光量単位はルーメン（光束）で指定、平行光源はルクス（垂直照度）で指定、スカイライト（IBL）は 1㎡ あたりカンデラ(cd/m2)つまり輝度で指定、とあります。本記事の説明通りですね。単位が違うので、指定する値もそこらへんを考慮して数値の大きさの違いを解釈する必要があるわけです。

BRDFを光の単位という意味できちんと考えてみる

　さて、初回からたびたび話に出てきたBRDF（双方向反射分布関数）をもう少し詳しく見てみましょう。BRDF$f_r(x,\omega,\omega')$は感覚的な説明としては「ある地点xに$\omega'$方向から入射した光のどれだけが、$\omega$方向へ反射するのか」という反射分布を示す関数（確率密度関数）ということになります。

　ただ、定義をより正確に見ると、「入射する放射輝度と反射する放射輝度の比」ではないという注意点があります。BRDFは、入射光については実は単位が放射輝度ではなく、放射照度になっているのです。

f_r(x,\vec \omega',\vec \omega) = \frac{d L_r(x,\vec \omega)}{d E(x)} = \frac{d L_r(x,\vec \omega)}{L_i(x,\omega' )(\vec n \cdot \vec \omega') d \vec \omega'}

　書籍「CG Magic」⁷によれば、このような定義にすることで、面の法線の向き（逆に言えば入射光が差し込む角度）による陰影の変化（第１回目の記事でいうところの「入射光の薄まり具合」）をコサイン項がBRDFとは式の上で分離した項として担当することができ、その結果、BRDFは純粋に物体の材質そのものによる反射特性を示すことに役割を専念できるから、ということのようです。これは主に、放射輝度（または輝度）でライティング計算するときのことを言っているのでしょう。

L_r(x, \vec \omega) = \int_\Omega f_r(x, \vec \omega', \vec \omega)(\vec n \cdot \vec \omega') L_i(x, \vec \omega') d \vec \omega'.

ここで、BRDFをこちらの式の形として捉えてみてください。

f_r(x,\vec \omega',\vec \omega) = \frac{d L_r(x,\vec \omega)}{L_i(x,\omega' )(\vec n \cdot \vec \omega') d \vec \omega'}.

　概念的にはコサイン項$(\vec n \cdot \vec \omega')$と乗算されて、その結果、分かりやすい放射輝度同士の入反射の比になりますね。その「比率」が入射放射輝度と乗算され、それが積分されるという、感覚的にも分かりやすい計算におちつくことになります。

そして、放射照度でライティング計算する場合は、BRDFをもう一方のこちらの式の形で捉えることになります。

f_r(x,\vec \omega',\vec \omega) = \frac{d L_r(x,\vec \omega)}{d E(x)}.

放射照度$E(x)$と乗算された結果、$L_r(x,\vec \omega)$になりますね。こちらはもっとシンプルでわかりやすいですね。⁵

L_r(x) = f_r(x,\vec\omega', \vec\omega) E(x).

第１回目のコラムの答え「ランバート反射の考え方」

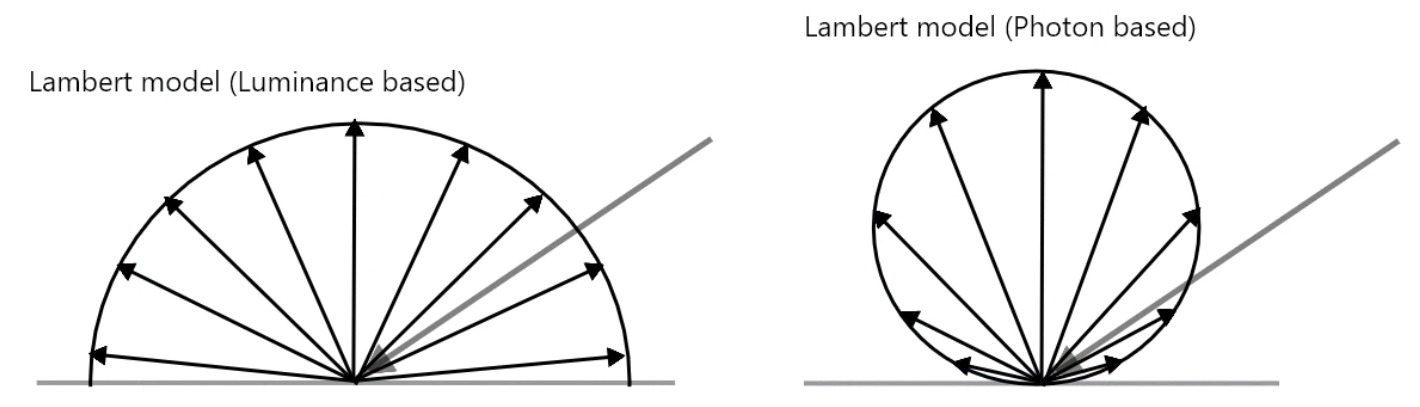
さて、第１回目の１つ目のコラムで、ランバート反射の図には基準によって図が二種類あるとお話ししました。

左の図は明るさ（輝度）ベースなので、私たち人の目の感覚的にわかりやすいですが、右の図（フォトンベース）は一体、何を示しているのでしょうか。

これは、実際の光子（フォトンベース⁸）で考えた時の、実際の光の物理的挙動としての反射具合を表しています。なので、光の挙動としては左の図ではなく右の図の方が正しいです。

それなのになぜ私たちの目には、結果的な目に見える明るさとして、ランバート反射が（左の図のような）どの方向から見ても同じ明るさに見えるのでしょうか。

実は、これはランバート反射の概念の提唱者であるJohann Heinrich Lambert（なんと、１８世紀の時代の方です）という方による「ランバートの余弦則」を読み解くことで見えてきます。

というか、Wikipediaの説明読めば早いのですが、このシリーズらしく柔らかく説明してみましょう。

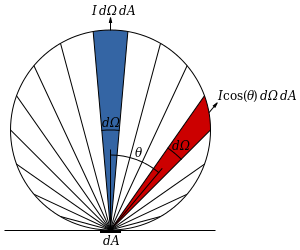
(Wikipeida「ランベルトの余弦則」のページから引用)

まず、Wikpediaから引用してきた上の図を見てみます。光が真上（法線上）に反射する光量（フォトンの量）を$I$とすると、理想的なランバート面の物理的特性として、角度Θ分斜めの方向に反射する光量は$I cos\theta$に減少するとされています。これはまさに、上の二種類あるLambert反射の図のうちの右側（フォトンベース）の図そのものですね。

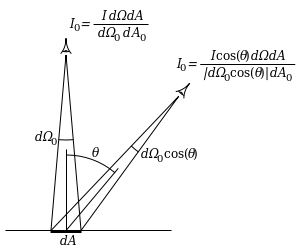
(Wikipeida「ランベルトの余弦則」のページから引用)

しかし、この斜めの方から反射面を観察するとき、観察者（ここではカメラとしましょう）から見た時の反射面は当然斜めに見えていますよね。斜めに見える、ということは、見え方的に面積が小さくなっているということです。ちょうど同じで$cos\theta$をかけた分に小さくなっているのです。

ここで思い出しましょう、放射輝度（または輝度）の単位は

放射輝度＝放射束／面積／立体角
また、
輝度＝光束／面積／立体角

なのでしたね。これが、分子の放射束（光束）が$cos\theta$をかけた分小さくなった。でも、分母の面積も$cos\theta$をかけた分小さくなっているのです。分子と分母が同じだけ小さくなっているのだから、打ち消しあって結局どの方向から見ても輝度が一定になる、という計算になります。これが、Lambert反射がどの方向からみても同じ明るさ（輝度または放射輝度）で見える理由です。

また、別の説明の仕方もできます。

斜めから見た時、反射してくる光量が$cos\theta$をかけた分小さくなるわけですが、実は反射面の面積だけでなく、それを捉えている視覚上の立体角も小さくなっています。立体角が小さくなるということは、観察者（カメラ）のイメージセンサーに入射してくる全角度からの光量計算に占める寄与率も小さくなるということです。同じ寄与率になるように、小さくなった立体角に$1/cos\theta$を乗算して元の立体角に戻してみましょう。すると、立体角が大きくなるわけですから、その新しい立体角に収まる注目すべき反射面の面積も広くなりますよね。面積が増える分入ってくる光量も増えます。それで、同様に輝度計算上はつじつまが合う（一定になる）ことになるのです。

まとめ

　いかがでしたか？　ちょっと難しかったでしょうか？　慣れないとそうですよね。こればっかりは、にらめっこしながら徐々に頭を慣らしていくしかなさそうです。私も最初はなかなか理解できず、関連書籍を何度も何度も読み直したものです。

　「柔らかく説明してみる」シリーズとしてはちょっと固すぎたかもしれませんが、ここらへんをずっと避けてしまうと、本当にいい加減な理解のままで解説を終えることになってしまい、それはさすがにCGを多少かじる者として、許容できませんでした。
　物理ベースレンダリングは決して、BRDFの各項の式をシェーダーコードに落とし込んで、ちょっとリアルそうな反射になったら「わーい！できた！」ではありません。光の単位も含めて、できる限り正確に物理量を取り扱おうという努力が重要です。

　誰が呼び始めたのかわかりませんが、「物理ベース」という、そもそもの命名がかなり前衛的だとは思いませんか。何を持っての「物理ベース」なのでしょうか。第１回目で、定義らしき説明を何項目か挙げましたが、それだって現時点におけるPBR（物理ベースレンダリング）の動向における大雑把で慣例的な説明に過ぎません。人によっては異論すらあるはずです。とはいえ、もちろんあまり細に入りすぎても互いの議論が難しくなりますし、やはり文脈やケースによって、「物理ベース」に対する捉え方はある程度柔軟であるべきでしょう。

　さて、固い話はこのくらいにして、次回からはもう少し実践的な話題に戻ろうと思います。とはいえ、具体的に何にするかはまだ思案中です。どうしましょうかねぇ……。

1. あるWebページの説明（ https://www.ccs-inc.co.jp/guide/column/light_color/vol04.html ）では、放射量の考え方（計測）の１つとして、放射束$P_1$Wの光を黒体（あらゆる光を１００％吸収する理想的な物体）に時間$t_1$照射した結果の温度上昇$T_1$と、同じ黒体に対して$T_2$時間電力$P_2$Wの電流を流しその電気エネルギーによって起きた発熱量$T_2$。この２つの発熱量が等しくなるように（$T_1=T_2$）両者を合わせた場合、その関係から電気エネルギー量は既知とすれば一方の光エネルギーを計測したことになると説明していました。光エネルギー⇔熱エネルギー⇔電気エネルギー間の１００％変換を前提としていますが、なるほど…。ちなみにこれが放射量の定義そのものかどうかは私は知らないです。 ↩

2. 実は、この「分光視感効率」は人によって多少のばらつきがあります。たまに「あなたにはこれが何色に見えますか？」みたいな謎掛けの写真を見せられたことがあるかと思います。これは、人間の眼の受容体（桿体（かんたい）や錐体（すいたい）と呼ばれます）の特性や比率に個人差が若干あるためで、いわば人によって物の明るさや色の見え方が完全に同じではないことを確かめる簡易試験の一種といえます。 ↩

3. 人によって感じ方に若干の差があるということは、何らかの平均的・標準的な基準がなければ測光量を定義することができません。今日では、CIE（国際照明委員会)という団体が定めた（いろんな人で実験して統計した）「標準分光視感効率」が基準とされています。 ↩

4. 世の中には、色弱や色盲といった、色を感じることが困難なハンディを持っている方もいらっしゃるのが現実です。4K8KだHDRだ広色域だとテクノロジーが進歩する一方ですが、より住みよい時代を作っていくには、今後はそういった方々への配慮もたいへん大事になってくるでしょう。 ↩

5. ただし、楽は楽なのですが、「BRDF*放射照度」の式は何にでも適用できるわけではありません。これがCook-Torranceベースのスペキュラ反射になると若干話がややこしくなります。というのも、ディフューズと違い、スペキュラBRDF自体がライトベクトルの情報を必要としています。そのため、平行光源や点光源など、ライトベクトルがわかるものであればともかく、IBLなどの場合でプレフィルタリングされた放射照度または照度テクセルのみを得ても、そのままでは計算が行なえません。ここらへんはSpecular IBLの場合、特別な方法があるのですが、それは別の機会に説明します。 ↩ ↩² ↩³ ↩⁴

6. あくまで、点光源の放射状の光の広がりを考慮して放射照度の式を立てるとそういう形になるだけであり、「放射輝度にコサイン項をかけることで放射照度に変換します」という言い方はいささか誤解を招くような気がします。 ↩ ↩²

7. 倉地紀子「CG Magic：レンダリング」オーム社， 2007 ↩

8. フォトンベース、つまり光のエネルギーに着目した話になりますが、そういう意味では最初の光の単位の表でいうと「放射輝度（または輝度）ではなく、放射強度（または光度）で話を論じている」ということでもあります。 ↩