この記事の狙い
- 本記事は、「シェーダーを触り始めてLambertやPhong反射までは作れる」くらいのレベルを最低ラインとして読者層を想定しています
- 説明の厳密さより、感覚的にイメージの湧きやすい説明の仕方を重視します。数式も少なめです。
- 厳密な説明を求める方は、他の記事にあたってください。
- 第1回と第2回もどうぞ。
前回まで
前回はdiffuse BRDFについて紹介しました。その次は素直にspecular BRDFについて紹介すればよいはずですが、このシリーズなぜか寄り道してしまいます。
今回はレンダリング方程式について考えてみましょう。
レンダリング方程式とは
皆さんは「レンダリング方程式」という言葉を聞いたことはありますか? このレンダリング方程式1は、今日のCGにおけるレンダリング処理の根幹をなす方程式です。
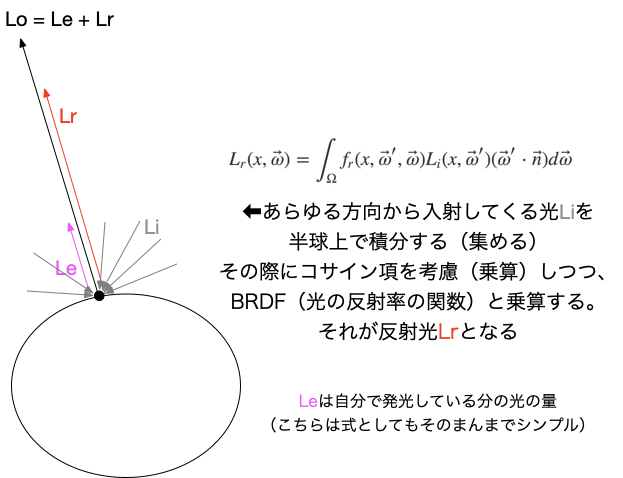
まず、物体上のある点xにおいて、ある方向$\vec \omega$(正確には単位立体角(単位はステラジアン)と言います)に放射する光の量(正確には放射輝度といいます)を関数$L_{o}(x,\vec{\omega})$で表すとします。
$L_{o}(x,\vec{\omega})$は次の2つの項に分けて考えることができます。
L_{o}(x,\vec{\omega}) = L_{e}(x,\vec{\omega}) + L_{r}(x,\vec{\omega})
$L_{e}(x,\vec{\omega})$ は自己発光する物体(蛍光塗料やもちろんライトなどの発光物も含まれます)が自ら外に($\vec{\omega}$に)向かって放射する光量を表しています。発光(emission)だから、頭文字のeがついています。
$L_{r}(x,\vec{\omega})$ は、他から入射してきた光を物体上の点xから$\vec{\omega}$にむかって反射する光の量になります。反射(reflect)だから頭文字のrがついています。
さて、$L_{r}(x,\vec{\omega})$の項はさらに次のように書くことができます。
L_{r}(x,\vec{\omega}) = \int_{\Omega} f_{r}(x,\vec{\omega}',\vec{\omega}) L_{i}(x,\vec{\omega}') (\vec{\omega}' \cdot \vec{n}) d\vec{\omega}
つまり、レンダリング方程式の式全体としては、次の形になるわけですね。
L_{o}(x,\vec{\omega}) = L_{e}(x,\vec{\omega}) + \int_{\Omega} f_{r}(x,\vec{\omega}',\vec{\omega}) L_{i}(x,\vec{\omega}') (\vec{\omega}' \cdot \vec{n}) d\vec{\omega}
「ぎゃああああ!」「数式極力出さない言うたやん!」という声が聞こえてきそうです。
しかし、全く出さないとは言わなかった・・・。冗談です。ちゃんと説明しますから、なんとか頑張ってついてきてください。
積分 $\int_\Omega$の中にある$f_{r}(x,\vec{\omega}',\vec{\omega})$を見てください。何か懐かしくないですか? そうでもない?(笑) これはBRDFです。そうです。思い出しましたか?
そして、過去の記事のこんな説明もあったのを思い出してください。
================================(回想ここから)====================================
================================(回想ここまで)===================================
積分記号はとりあえずおいといておきましょう(なんかよくわからないですもんね!)
レンダリング方程式の一部 $f_{r}(x,\vec{\omega}',\vec{\omega}) L_{i}(x,\vec{\omega}') (\vec{\omega}' \cdot \vec{n})$ と、回想で説明した反射の式 $f_r(x,\vec\omega', \vec\omega) (L \cdot N) i_d$ なんか似てないですか?
BRDFである $f_{r}(x,\vec{\omega}',\vec{\omega})$ は共通ですね。
$L_{i}(x,\vec{\omega}')$って何かというと、これは入射光でして、これってつまり$i_d$(光の強さ)と対応します(厳密にいうとほんの少しだけ意味が違うんですが)
そして、 $(\vec{\omega}' \cdot \vec{n})$ ですが、この$\vec{\omega}'$って実は入射する光の方向を表していて、つまりはライトベクトルLなんですよね。つまり回想の式の$(L \cdot N)$(つまり、コサイン項)に相当するのです。
え、ということは……そうですね。私達は今まで、レンダリング方程式の一部をシェーダーで計算していたことになるのです! これは発見ですね。2
レンダリング方程式は再帰的に考えることができる
さて、以下のレンダリング方程式ですが、図で考えてみましょう。
L_{o}(x,\vec{\omega}) = L_{e}(x,\vec{\omega}) + \int_{\Omega} f_{r}(x,\vec{\omega}',\vec{\omega}) L_{i}(x,\vec{\omega}') (\vec{\omega}' \cdot \vec{n}) d\vec{\omega}
図にすると分かりやすいですね。さて、ここで疑問です。色々な方向からやってくる入射光$L_i$ですが、これらはどういう過程をたどってやってきたのでしょうか。もしや……。
そうです、これらの入射光も、レンダリング方程式の理論によってまた考えることができるのです。
これら入射光も、もとを辿れば(光源から直接放たれた光でない限り)、他の物体で起きた放射(反射)によってやってきた光のはず……。
つまり、式としては、こんな感じに$L_i$を展開できます。
L_{o}(x,\vec{\omega}) = L_{e}(x,\vec{\omega}) + \int_{\Omega} f_{r}(x,\vec{\omega}',\vec{\omega}) L_{i}(x,\vec{\omega}') (\vec{\omega}' \cdot \vec{n}) d\vec{\omega} \\
ここで L_{i}(x,\vec{\omega}') = L_{e}(x_2,\vec{\omega_2}) + \int_{\Omega} f_{r}(x_2,\vec{\omega_2}',\vec{\omega_2}) L_{i}(x_2,\vec{\omega_2}') (\vec{\omega_2}' \cdot \vec{n_2}) d\vec{\omega_2} \\
つまり、
L_{o}(x,\vec{\omega}) = L_{e}(x,\vec{\omega}) + \int_{\Omega} f_{r}(x,\vec{\omega}',\vec{\omega}) \left( L_{e}(x_2,\vec{\omega_2}) + \int_{\Omega} f_{r}(x_2,\vec{\omega_2}',\vec{\omega_2}) L_{i}(x_2,\vec{\omega_2}') (\vec{\omega_2}' \cdot \vec{n_2}) d\vec{\omega_2}\right) (\vec{\omega}' \cdot \vec{n}) d\vec{\omega}
ますます複雑になってきました……。めまいがしますので、式をまともに追わなくていいです。なんとなくで。
つまりは、レンダリング方程式は、$L_i$について、再帰的に展開していくことができるんだよ。ということを理解できればいいです。
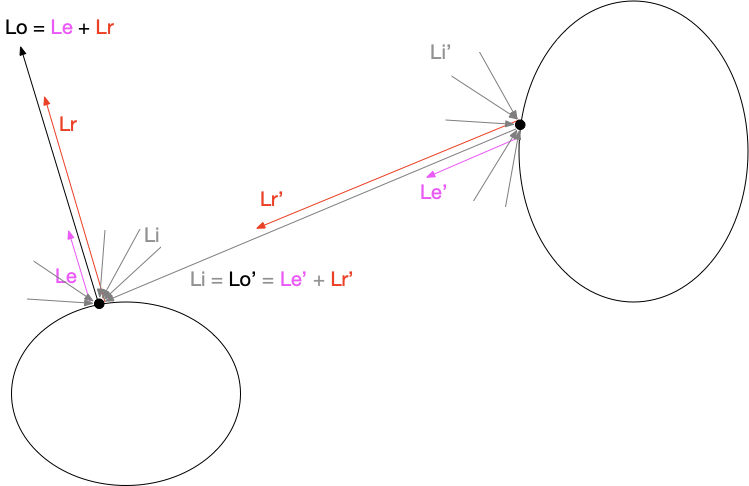
図にすると、そんな難しい話ではありません。
つまり、レンダリング方程式は、光が様々な物体にぶつかっては反射し、それがまた他の物体に入射してまた反射し……という、現実の世界で起きる光の複数回反射を計算することができる(いわば、「光の物体間の輸送」を計算することができる)方程式であるということです。
VRayやArnoldといった、映画CGなどでも使われるオフラインレンダラーでは、レイトレーシングと呼ばれるレンダリング手法が使われますが、これらのレンダラーは、このレンダリング方程式を計算しているのです。
ただし、レイトレーシングは光の進行方向とは逆に、カメラから「レイ(光線)」を飛ばして、光を逆方向に追跡します。というのも、光源からレイを飛ばすやり方だと、それが観察者のカメラの映像素子に相当するエリアに届くレイは一部なので、計算の効率が非常に悪いからです。
とはいえ、逆方向からレイを飛ばして計算なんて、してよいのでしょうか?
そこで重要となるのがBRDF(Bidirectional Reflectance Distribution Function)の性質です。実はBRDFは、入射方向と出射方向を入れ替えても、結果が変わらないという性質を満たした関数なのです。これをヘルムホルツの相反性と呼びます。
また、今日のゲームCGでも、限定的ながらこのレンダリング方程式を計算していると言っても良いでしょう。
さらにいえば、私達がLambertやPhongのシェーダーを書いて、「わーい、陰影がついたぞー♪」なんてやっているときも、このレンダリング方程式のごくごく一部を計算していたことになります。ただし、この場合は直接光のみを計算していることになります。レイトレーシングのように、再帰的に複数回反射してきた光まで追って計算しているわけではありません。
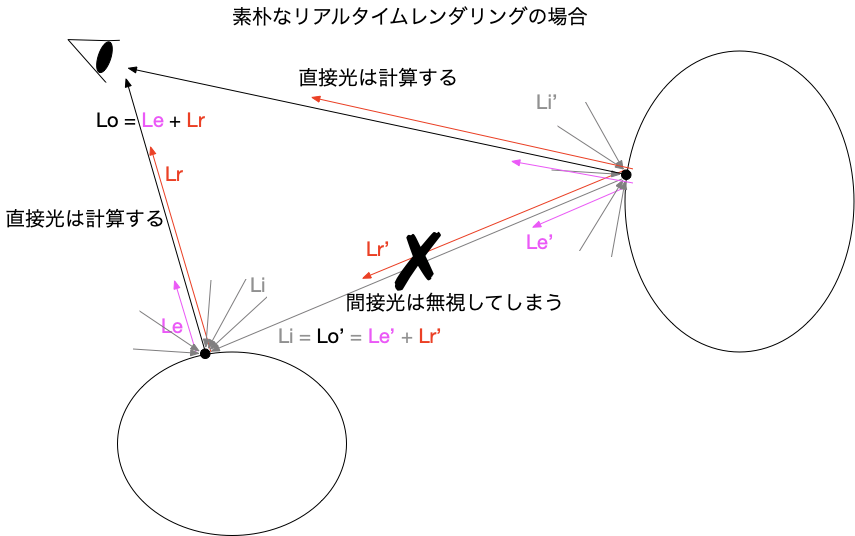
さて、複数回反射まで計算するのと、しないのとでは、レンダリング結果の絵はどう違ってくるのでしょう?
結論から言えば、直接光だけのレンダリングでもCGとしての綺麗な絵は出ます。ただ、どこか物足りなさを感じると思います。すこしCGっぽいというか、光の充満感がないというか空気感がないというか……そういう印象を受けるかもしれません。
つまり、本来存在しているはずの間接光(複数の反射を経てやってくる光)の分をそのまま無視しているわけですから、当然、本来よりやや暗めかつ光のコントラストが強い絵ができあがります。
オフラインレンダラーや、GI(グローバルイルミネーション)を採用した最新のゲームエンジンで複数回反射まで計算したシーンを見てみると、少し……細かい部分がほんのりと明るいんですね。直接光しか計算しなかった絵に比べ、全体的に少し場が明るくなり、また細部の陰影の密度感が高まります。そんな感じの、より現実感のある絵になるのです。
本記事では、基本的にローカル反射のBRDFの文脈に限定して物理ベースレンダリングを説明していきます。つまり、複数回反射までは考えない物理ベースレンダリングです(それだけでも覚えることは山程あります)。ですが、CGの考え方の背景としてこのようなことがあるということは覚えておいてください。
FAQ
Q:最近のゲームCGでディファードレンダリングという用語を聞くけれど、ディファードレンダリングでないと物理ベースレンダリングはできないの?
A: ディファードでなくてもできます。
ディファードレンダリング(Deferred Rendering)とは、GPUのリアルタイムレンダリングにおいて、通常のレンダリング方式(フォワードレンダリング)と異なる、大量のライトを処理するためのレンダリング方式です。
フォワードレンダリングが、一回のレンダリングで描画物のシェーディングを一気に行うのに対し、ディファードレンダリングは工程を分けます。
最初にGバッファ(ジオメトリバッファ)という、3Dシーンの幾何学情報をバッファにレンダリングし、その後で複数のライトをポストプロセス式にライティング処理を重ねていく方法になります。
数年前より、ディファードレンダリングがゲームCGでもてはやされるようになったのは、通常のフォワードレンダリングと比べて、より大量のライトを処理できるからです。
リアルなレンダリングを行うには、BRDFだけが物理に基づいたリッチなものというだけでは足りません。現実の世界では、我々が考えている以上の光源が周りに存在します。それほどの光源があるために、我々の世界は複雑多様な光に満ち溢れており、それが眼の前の世界を現実足らしめているのです。そのため、ゲームCGでも本当にリアルなシーンを作るには、大量の光源(ライト)をシーンに配置しなければなりません。
ディファードレンダリングは、それだけの大量のライトを処理するためのレンダリング設計の一つであり、それ自体が物理ベースレンダリングの考えと直結しているわけではありません。
逆に言えば、我々がライティングを実装するときの、一番簡単で素朴なやり方である、普通(フォワードの)レンダリングのやり方でも、(ローカル反射の枠内でという意味ですが)物理ベースレンダリングはできる、ということになります。
さいごに
さて、このレンダリング方程式やBRDFを考える上では、本来、放射輝度や放射照度という光の量の単位についてきちんと学んでいなければなりません。それを、学習の敷居を下げるために、本記事ではあえて定義の説明を飛ばして解説を行っています。
しかし、次回以降でこれらの光の単位についての学習をやります。そして、そのときにこれらレンダリング方程式やBRDFの定義をふたたび振り返ることになるでしょう。
追記:結局みんな待ってたと思うので(ほんとか?)、第4回目の内容は鏡面反射BRDFにしました。