この記事の狙い

　近年、最新のテレビゲームやVRコンテンツ等で、写実的な３Dグラフィックスは珍しいものではなくなりました。
　これらの多くには「物理ベースレンダリング」という手法が用いられています。

　この記事シリーズでは、UnityやUnreal Engine、Three.jsなどでCGコンテンツを作った経験がある人を想定し、次のような知見の手助けとなることを目的としています。

物理ベースレンダリングのイメージを掴んでもらう。
物理ベースレンダリングを自分で実装するための情報を提供する。
世の中にある物理ベースレンダリング対応のアセット素材をUnityやWebGLライブラリで活用するのに必要な知識を提供する。

前提（おことわり）

あくまで「なんとなくわかりたい人向け」の記事です。ネット上には物理ベースレンダリングについての良記事がたくさんありますが、多くは厳密性を重視しており、数式も沢山あるために初学者にはハードルが高いと思います。
このシリーズでは、厳密さよりも一般の人にもイメージを持ってもらえるよう、感覚的な説明を行います。明らかに間違った説明やたとえは避けるように努めますが、厳密さを求める方には全く向かない内容であることをご承知おきください。
最初は数式をあまり出さないようにします。しかし全く数式無しで物理ベースレンダリングを説明することは不可能なので、次第に増えてくる点はご了承ください。

想定する前提知識

　以下のレベルを想定しています。

Three.jsやUnityなどを使って、何らかのCG・ゲームコンテンツを作ったことがある。
Lambert反射とPhong反射までは、だいたい理解している。
それ以上のCGの知識を勉強したいという熱意がある。

おさらい

　古典的なライティングについておさらいしましょう。
　まずは一番単純なLambert反射です。シェーダーを勉強し始めた頃、一番簡単なライティング計算として次のような式をシェーダーコードとして書かれたことがあると思います。

L_r = \rho_d \times (L \cdot N) \times i_d

$L_r$は、光の入射が起きた点から、ある方向（大体は観測者の方向）へ放射（反射）する光の量です。放射と書いたのは稀にですが反射だけでなく自ら発光する物体もあるためです（といっても、上式では自己発光の項は無視していますが）。
$\rho_d$ はLambert反射における反射率です。
$(L \cdot N)$はコサイン項といいます。法線と入射光のベクトル同士が離れた方向になるほど、この値が小さくなることは知っている方も多いと思います。
$i_d$は入射光の強さになります。

※ 初心の方でも受け入れやすいよう、ここでは厳密な書き方を避けていますが、記事の回を追うごとに詳細を突き詰めていきます。
※ 実際は、コサイン項がマイナスにならないように $max(0, L \cdot N)$ とするものですが、本質ではないので省いています。

　この式をシェーダーコードとして実行すれば、ライトを一つ配置しただけで、それなりになだらかな物体の陰影が得られることでしょう。
　本記事では、この辺りまでを自力でやれる方をミニマムレベルと仮定して話を進めます。

物理ベースレンダリングとは

　物理ベースレンダリングの定義について、はっきりとした標準化は行われていません。最低限満たすべき要件についてのなんとなくのコンセンサスはあるようですが、それもリアルタイムCG（ゲーム等）やオフラインCG（VFX業界）等では、重視する点にずれもあることでしょう。本記事著者の捉え方を一言で表すなら、次のようになるでしょう。

光の反射や屈折といった現象を、物理的な根拠に極力基づいて計算するレンダリングである。¹

　より具体的には、物理的根拠に基づくために次のような事項を守ることが原則となっています。

光の計算に用いる反射モデルの式に、物理的な根拠に基づいたものを採用している。
採用する反射モデルが、エネルギー保存則を満たしている。つまり反射時に、物体表面から反射して出ていく光量が、入射してくる光量を超えない。
レンダリング対象の物質の素材（マテリアル）のパラメーターが、現実に存在する素材の物理的特性を反映した値になっている。
CGの計算の過程において、データの入力から出力装置（ディスプレイなど）までを通じて、正しい取扱いになっている。

いきなり柔らかくない表現が出てきました。しかし最初のイメージをあやふやにすると良くないので、ここで一旦、明確化します。
それぞれ、以降で説明していきます。

1. 「光の計算に用いる反射モデルの式が、物理的な根拠に基づいている」とは？

　この記事の想定する読者は、最低でもLambert反射（なだらかな反射）やPhong反射（ツヤっとした反射、イラストレーターさんなら「ハイライト」などと呼んだりするかもしれません。ああいう感じの反射を実現するものの一つです）についてはある程度知識があることを想定しています。

　「反射モデル」とは何かと言うと、具体的にはこうしたLambert反射やPhong反射といった計算式のことを指しています。

これらの反射モデル（物理ベースなものも、Lambert反射モデルやPhong反射モデルも含みます）は、別名でBRDF（Bidirectional Reflectance Distribution Function：双方向反射率分布関数）とも呼ばれます。

　BRDFは、光の入射方向、物体表面上の光の入射・出射がなされる位置座標、そして光の出射方向（反射して出ていく方向）という３つを引数にとる確率密度関数です。
　その関数の意味を言葉で説明すると「ある材質の物体表面のとある位置ｘに、ある方向ω'から光が入射してきた時、別の方向ωへと出射していく光の確率（割合）はどれくらい？」という意味になります。

f_r(x, \vec \omega', \vec \omega ) = (BRDFの種類によっていろいろ)

　実際は、入射した位置ｘがそのまま光の出射位置になるとは限らず、物体表面下で散乱を繰り返した結果、少し離れた位置x'から光が出ていくケースもありえます。これを扱う関数もあって、BSSRDFというのですが、これは流石に計算が重たすぎるので、多くの場合はある程度状況を限定して、BRDFで済むケースのみで運用することが多いです（逆に言うと、全てのケースや材質を扱えるとは限らなくなります）。

　物理ベースレンダリングの理論では、このBRDFという単語が頻出します。といっても、全てのBRDFが物理的根拠に基づいているわけではありません。言ってしまえば、前述の通り、LambertやPhongもBRDFの一つです。²

　ではLambert反射やPhong反射は物理的な反射モデル（BRDF)ではないのでしょうか？

Lambert反射

　Lambert反射とは、入射した光がどの方向から見ても同じ明るさに見えるように反射する反射モデルのことです。
　現実世界には、そんな風に単純な反射をするような物質は存在しません。ですが、CGの世界ではそうした極端に単純な反射特性の方が数学的にシンプル（言い換えると、計算が軽い）なので、昔からよく使われます。
ということは……Lambertは物理的な根拠に基づいた反射方式（CG分野の人は「反射モデル」とよく言います）ではありません。

LambertのBRDF式は以下のとおりです。

f_r(x,ω',ω)=ρ_d

ここで、$ρ_d$は定数になります（定数ですから、それはもう計算は軽いですね）

「えっ、定数なの？仮に$ρ_d$=1.0とかだったら、f_r(x,ω',ω) = 1.0 なの？　そんな単純でいいの？」と思われるかもしれません。ですが、そうなのです。

「光が入射する角度（正確には物体の表面法線と入射方向の内積）によって、Lambertでも反射の具合がなだらかに変化するじゃない！」

と思われた方もいらっしゃるかと思います。そのとおりなのですが、そのなだらかな変化は、（Lambert反射の場合は）BRDFでは処理されないのです。実際は、ローカル反射全体の式の中で、BRDFの隣に居る余弦項（コサイン項ともいいます。具体的には物体表面法線ベクトルと入射方向ベクトルの内積です）がその変化を担当します。

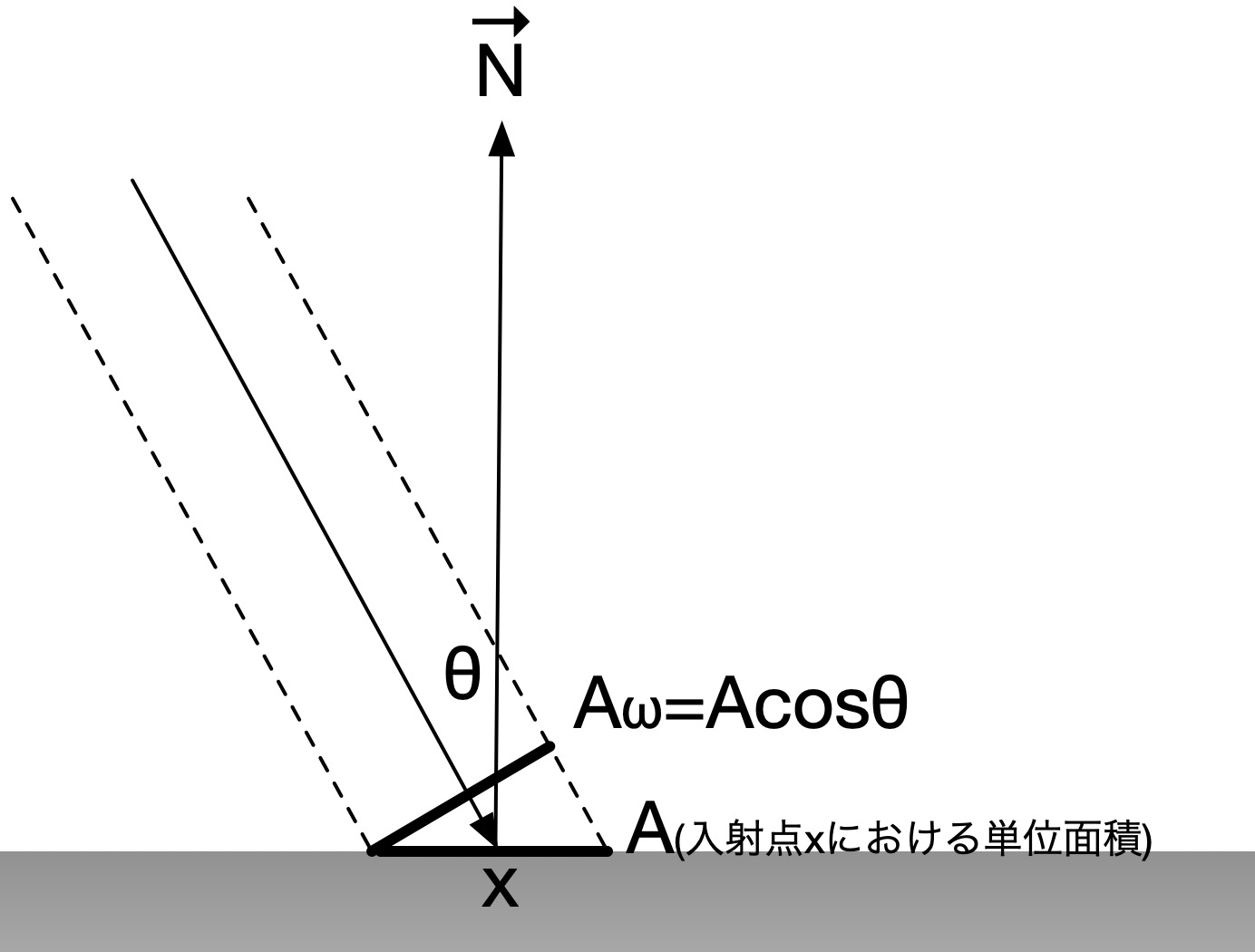
　この図を見ると、光の計算で着目している点X上の計算対象となる単位面積Aに対して、光が入射する向きが傾けば傾くほど、光の筋の断面面積Aω=Acosθは、小さい値になっていきます。それが、より大きな面積である単位面積Aに射影されるわけです。
　感覚的になんとなく、光が斜めから差し込むと、単位面積上は光が薄まってしまうことが想像できると思います。

　実際に計算式の上でも、以下の関係がなりたちます。つまり、入射光が斜めから差し込むことによる光の薄まり具合はコサイン項で考慮することができるのです。

E_\omega = \frac{\Phi}{A_\omega} = \frac{\Phi}{A \cos\theta}
\\
E = \frac{\Phi}{A} より
E = E_\omega cos\theta

　Lambert反射でのなだらかな陰影の変化は、Lambert BRDF（定数）によるものではなく、このコサイン項の仕業であることを覚えておいてください。逆に、コサイン項が変化しない条件下であるなら、Lambert BRDFは定数であることから、どの方向から見ても同じ明るさに見えるように反射するのです。

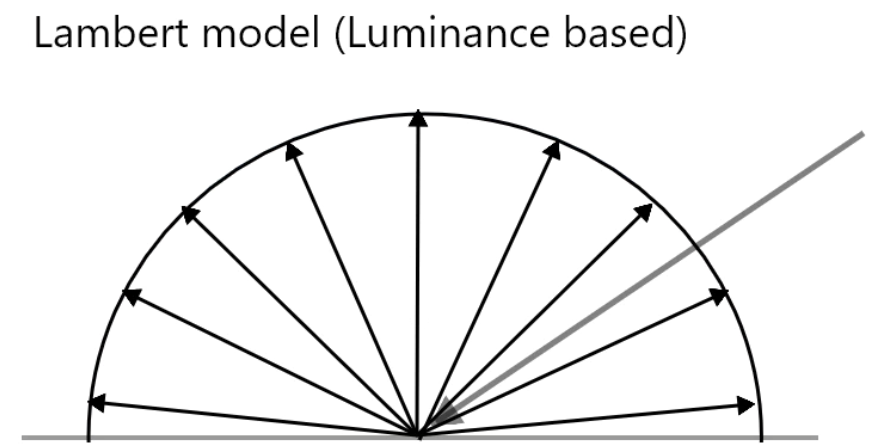
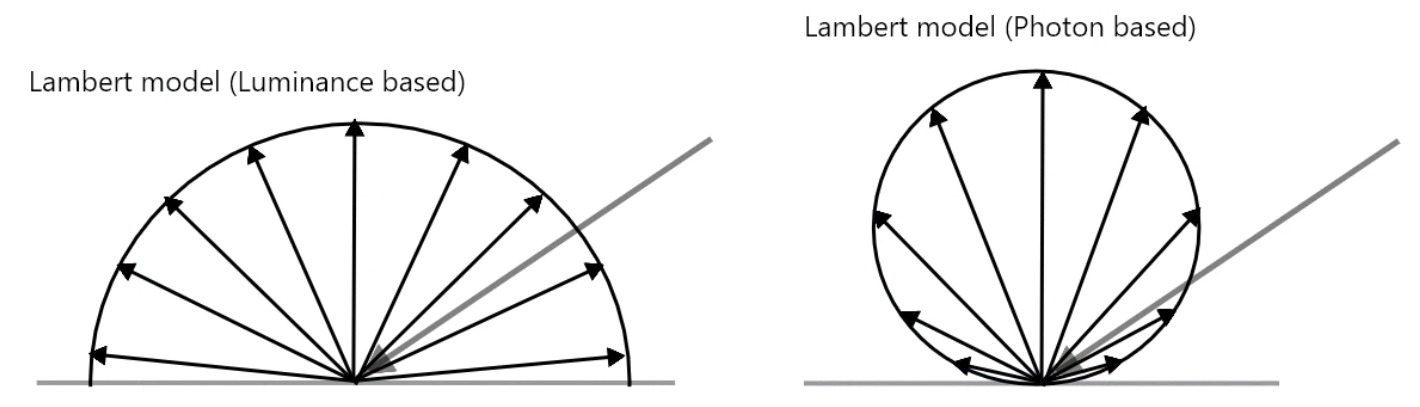
コラム１：Lambert反射の正しい図はどっち？？

CGについてちょっと突っ込んで勉強している方は、ランバート反射の図として上の２つの図のうち、左ではなく右の図（Photon Basedと書いてある方）がLambert反射の図であるという説明を見たことがあると思います。
いったい、どっちの図が正しいのでしょうか？

実は、これは基準によります。単純に各方向から見た「明るさ（光学的には輝度といいます）」という意味で考えると、左の図（Luminance Basedと書いてある方）の方がふさわしい図です。CGのシェーダーで単純にランバート反射の式を書いて、レンダリングさせてみた時の、あの映り方ですね。なんとなく感覚的にわかりやすいですよね。

しかし、より物理的な意味……光の光子（フォトン）という意味で考えると、実は右の図（Photon Based）の方が正しいのです。

これの詳細については、第５回で詳しく説明しようと思います。今回はシリーズの最初です。話を単純化するために、この第一回目の記事では、左の図、つまり「明るさ（輝度）」ベースの考え方で説明を行います。

（混乱してきた方は、とりあえず右の図は忘れてください）

Phong反射

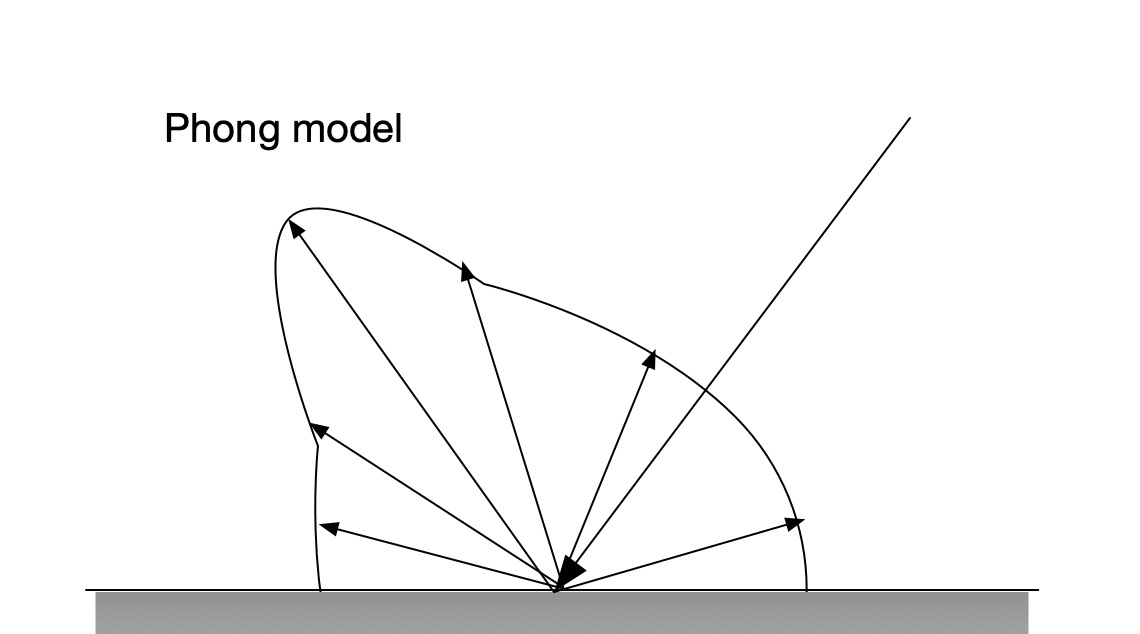
（図がだいぶ雑になりました。この形をそのまま鵜呑みにしないでください。あとこれも輝度ベースでの形とお考えください💦）

　Phong反射（今後、こうした反射の種類は「反射モデル」と呼ぶことにします）も、それっぽくハイライト（CG分野の人はハイライトではなく「スペキュラ」と呼びます。本記事でも今後は「スペキュラ」というようにします）を出すための経験則的に作られた簡易計算モデルで、実際の物理的な光学現象を基づくものではありません（基づいてはいませんが、似るように参考にはされています）。

　上の図で、半円状から少し飛び出して尖っているあたりが、スペキュラ反射成分の方向と強さを表しています。

　ちなみに、反射の方向と強さを表すこうした形をCG用語で「反射ローブ」と呼びます。

　Phong反射モデルは、実はspecular反射だけでなく、diffuse反射（Lambert反射）や環境光までを含んだ式になっています。上のローブの図で、突起部分以外もまんべんなく面積があるのは、Lambert成分によるものです。

L_r = k_a i_a + ρ_d(L \cdot N)i_d + ρ_s(R \cdot V)^α i_s

（上記はライトが１つの場合）

あえて、specular反射部分だけ取り出すと、Phong BRDFは以下の形になります。

\frac{ρ_s(R \cdot V)^α}{(L \cdot N)}

分母の内積はなにかというと、前述した入射光の傾きによる影響（コサイン項）を打ち消すために存在しています。

このPhong反射モデルも、そもそもPhongのBRDF部分自体が物理的な根拠に基づいたものではなく、またエネルギー保存という意味でも満たしていないものになっています。³

コラム２：Lambert（ランバート）とdiffuse（ディフューズ）は違うの？　phong（フォン）とspecular（スペキュラ）は違うの？

　つい混同してしまいますよね。
　現在のCGでは、光の反射は次の２種類に分解することができる、とされています。

diffuse（ディフューズ：拡散反射とも言います。なだらかに広範囲に広がって反射していくタイプの反射です）
specular（スペキュラ：鏡面反射とも言います。特定の方向に鋭く光が反射していくタイプの反射です）

実際、光の反射をdiffuseとspecularに分けて考えるこの方式は、CGを考える上での反射モデルの一種の単純化であり、近似であるのですが、多くの場合満足な結果を得られるということで、広く世に受け入れられています。

入射してくる光が、光学現象としてどうdiffuse反射とspecular反射に分かれるのか、ということについては、フレネルという光学現象が深く関わってくるのですが、それはまた次回以降の記事で説明します。

　さて、次の図をみてください（自力で図を書くのに挫折して、引用させていただきました…）

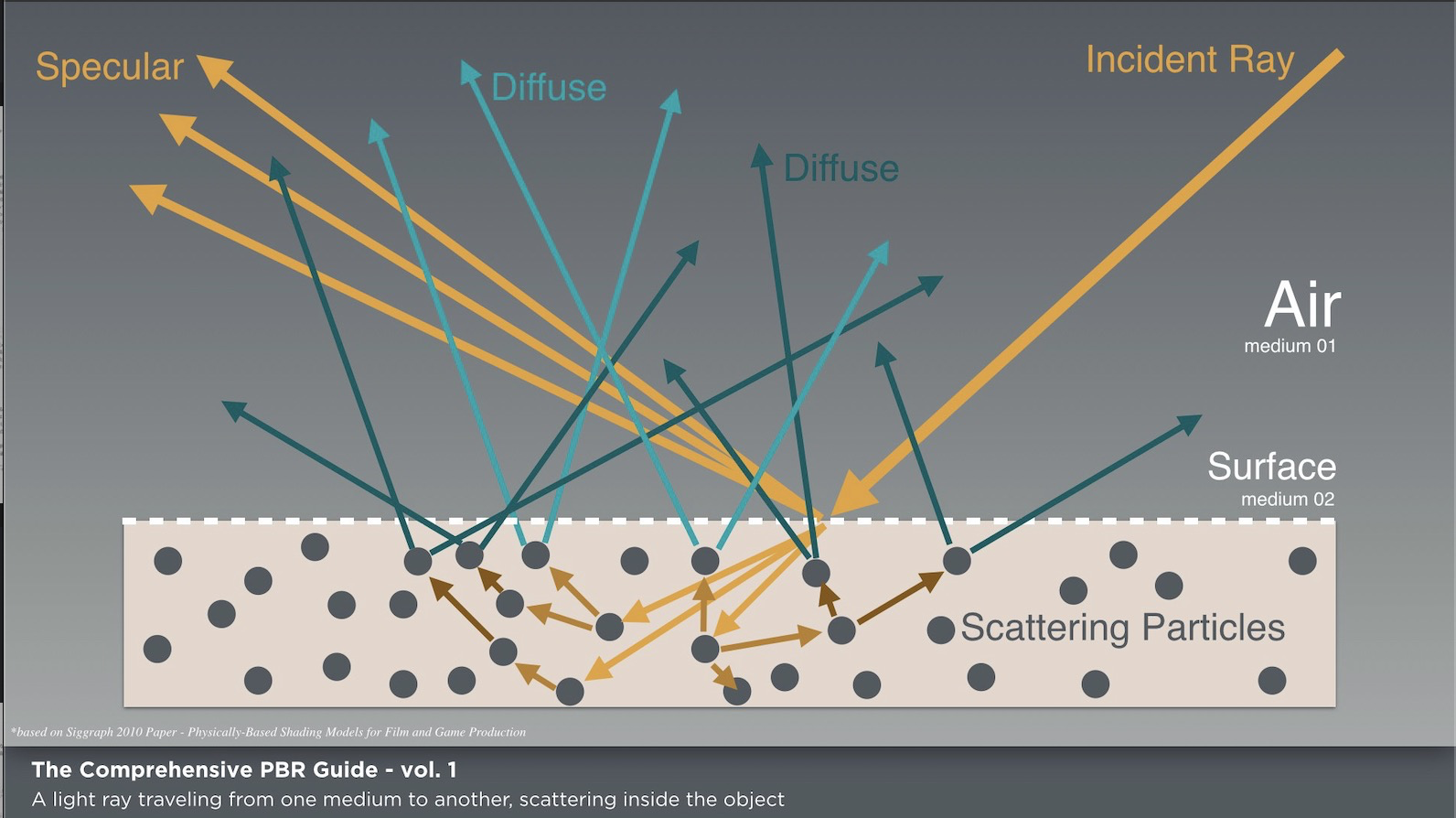
Wes McDermott「The Comprehensive PBR Guide by Allegorithmic - vol. 1 Light and Matter : The theory of Physically-Based Rendering and Shading」©Allegorithmic　から引用

上の図から伺えるように、diffuse反射とspecular反射は、反射に至るまでの過程が大きく異なることがわかります。その違いを考慮し、別々に計算できるようにするため、CGの反射の概念としても分離していることになります。

diffuse反射

物体表面に入射してきた光が、フレネル光学現象の結果、屈折して物体内部に一旦進入し、その物体の内部で様々な方向に散乱を多重に繰り返した結果、再び物体の外に出ていく（細かいことをいうと、ここでもまた屈折するのですが）光はdiffuse反射光と呼ばれます。この過程では、光の波長のうち物体内に吸収されてしまう成分も出てくるため、その結果、物体特有の色を帯びて（リンゴなら赤）我々の目に物体固有の色として知覚されることになります。

specular反射

物体表面に入射した光が、フレネル光学現象の結果、物体表面でそのまま反射した光になります。物体内部に光が侵入せず、光源の光がそのまま反射されるため、基本的には反射光は光源の色合いがそのまま残ります（例外もあります）。

　Lambert反射モデルは、diffuse反射にカテゴライズされる、具体的な拡散反射計算式の一つになります。

　Phong反射モデルは、Lambert反射（diffuse反射）とPhongスペキュラー反射、アンビエント項⁴まで複合させた反射式なのでややこしいですが、２つ目のPhong独自のspecular反射の成分のみを指してPhong反射と言及する場合があります。Phongと用語が出た場合には文脈に注意が必要です。⁵

　ちなみに、物理ベースレンダリングにおいても、基本的には反射をdiffuseとspecularに分けて考えます。

物理的な根拠に基づいた反射モデルとは？

　LambertやPhongは物理的な根拠に基づいていないといいました。
　逆に言うと、「物理ベースレンダリングでは、物理的な考慮がなされたBRDFを採用して光の計算をしている」ということです。

　物理ベースレンダリングについて調べようとしたことがある方は、「GGX」などといった単語をちらほら見かけたことがあると思います。GGXは、物理的根拠に基づいたBRDFを構成する計算式の一要素として、よく使われる関数です。

　では、「物理的な根拠に基づいたBRDF」とはなんなのか。主に具体的には次の点を持たしたものと言えます。

エネルギー保存を（概ね）満たしている（完全に満たしていない物も実は多いですが…それまた別の話で）。
BRDFを構成する幾何学モデルが、物理的な微細構造をきちんと考慮したうえで数式として導出されており、実際の想定した素材の実測値にうまくフィットしている。

逆に言うと、正規化Lambertや正規化Phongなどは、エネルギー保存を満たしているため、光の計算として大きな破綻は起こさないものの、それだけでリアリティのある映像を作り出せるものかというと、不十分な部分がありえるわけです。

　詳細は次回にしますが、今日のCGにおいては、光の反射に影響する「物体表面のミクロレベルの凹凸」を、その材質の物理的・幾何的な微細形状を考慮した、数学的な数式モデルとして数式化します。これが物理ベースのBRDFです。

　そして、その幾何学的なモデルとしては、マイクロファセットモデルというアプローチがよくとられます。これは、「物体表面のミクロレベルの凹凸」⁶を、様々な方向を向いた微細な平面の集まりと見なして（単純化して）、幾何学的・数式的に取り扱えるようにしようとする考え方のことです。

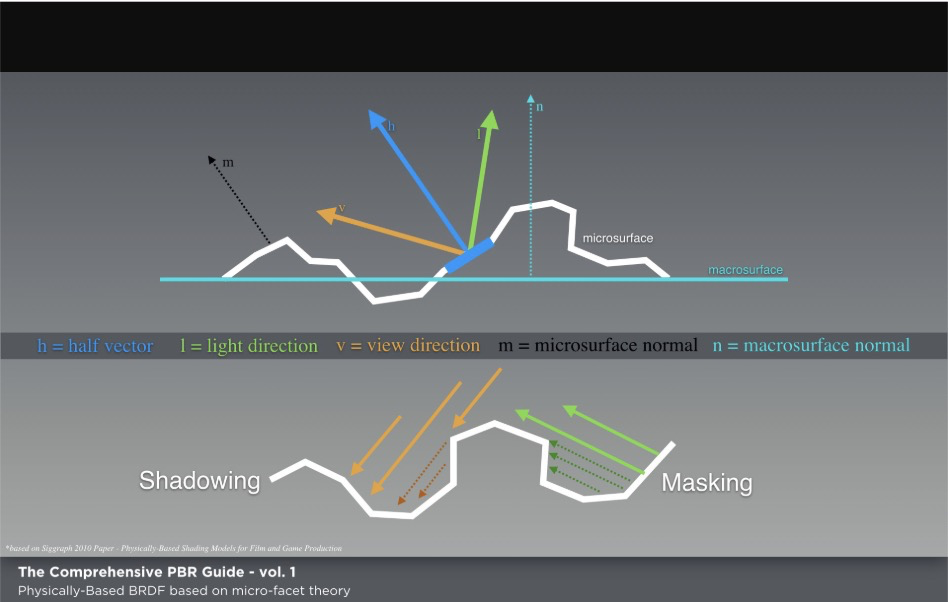
Wes McDermott「The Comprehensive PBR Guide by Allegorithmic - vol. 1 Light and Matter : The theory of Physically-Based Rendering and Shading」©Allegorithmicy より引用

　実際、光には粒子としての特性（幾何学的な問題として取り扱える）だけでなく、波動としての特性も持っているため、このマイクロファセットモデルに基づいていたからといって、全ての光学現象を正確に取り扱えるわけではないのですが（例外としては回折現象などがあります）、大体の光学現象は幾何学的な問題として取り扱えるため、マイクロファセットモデルは今日の物理ベースレンダリングの基礎的な考え方として普及しています。

2.　「採用する反射モデルが、エネルギー保存則を満たしている」とは？

　前述の物理的根拠に基づいている、とされるBRDFでも、ものや条件によってはエネルギー保存則を完全には満たしていないものがあります。⁷

　もしみなさんがシェーダーを手書きで書いたことがあって、素直にLambertやPhongを直書きしていた場合、たぶん満たしていません⁸

　特に昔のCGソフトウェアでは、diffuse反射やspecular反射などの各反射成分を単純に合算していたため、その結果、入射してくる光よりも物体表面から出ていく光の方が光量が増えてしまうケースもよくみられました。物理的に、そのようなことは（物体自体が発光している場合を除いて）起こりえません。
　昔のCGソフト（現在の最新のCGソフトでも、昔の時代のマテリアルを使ったりすると）では、そうしたCG計算をつい生み出してしまいがちでした。

　現在の物理ベースレンダリングでは、diffuse反射やspecular反射の成分を単純に足すのではなく、エネルギー保存則を満たすように調整するように配慮された計算モデルを導入しています。

エネルギー保存を満たさないとどうなるのか

　満たしていないとどうなるのか、というと、一言で言うと不正確な結果になります。
　別にレンダリングされる絵がぐちゃぐちゃになるわけではありませんが、見る人から見れば「明るさが説得力を失っている」ように見えるでしょう。

　現実世界では、あらゆるエネルギーは、エネルギーとしての形態は変われども、その量は保存されます。物理現象の全体としてその辻褄があってさえいえばよいのですが、エネルギー保存則を満たしていないBRDFは、いわば、現実世界から不正にエネルギーの一部を消失させたり、どこからともなく新たに出現させてしまっているのです。もはや神様のイタズラ？ですね。

　それはともかく、実際のCG計算においても、ただ一度の反射ならまだよいのですが、何度も反射を繰り返すと、そのたびにそのBRDFによってエネルギー総量が変わってしまいます。その結果、レンダリング結果が想定外のものになりえるのです。

　あまり反射を繰り返さないリアルタイムCGならまだ影響は軽微かもしれませんが、これが反射計算を何度も行うレイトレーシングなどになってくると、目に見えて異なる結果になることでしょう。

3.「レンダリング対象の物質の素材（マテリアル）のパラメーターが、現実に存在する素材の物理的特性を反映した値になっている」とは？

　たとえ、BRDFという、光の計算における関数が物理根拠に基づいていたとしても、その入力となるデータに物理的な根拠がなければ、その結果はやはり不正確になります。

　CGソフトや、UnityやUnreal Engineなどで使えるアセット素材集を探したことのある方は、「PBR対応マテリアル」といったものを見かけることがあると思います。あれらは、物理ベースレンダリングに対応した、物理的根拠に基づいたマテリアル素材集、ということになります。

（Khronos glTF-WebGL-PBRページより画像引用）

　これらの素材集の中身を見てみると、次のようなもので構成されていることに気づかれるでしょう。

ベースカラーテクスチャ

（Khronos glTF-WebGL-PBRページより画像引用）
(この素材の場合、テクスチャはグレースケールですが、別途ベースカラーファクター値として色を乗算して与えているようです)
メタリック・ラフネステクスチャ

（Khronos glTF-WebGL-PBRページより画像引用）
（この素材の場合、Roughnessがgチャンネルに、metallicがbチャンネルに入っています）
法線テクスチャ

[Khronos glTF-WebGL-PBRリポジトリより引用]

３つめの法線テクスチャも、今日のCGではリアルな品質を得るうえで重要な要素ですが、今回の物理ベースレンダリングという観点では、直接の関係はありません。物理ベースレンダリングに関わってくる、物体表面の構造は、顕微鏡レベルのもっとミクロなレベルの世界に注目することになります。

　ここでは、ベースカラーテクスチャとメタリック・ラフネステクスチャが主役になります。

　ベースカラーテクスチャは、まるで普通のディフューズ（模様）テクスチャのように見えますが、実際はもう少し複雑な取り扱われ方がなされます。具体的には、メタリックが０の時には「アルベド」（拡散反射に影響する。従来でいうならディフューズテクスチャに近い）として値が解釈され、メタリックが１のときには光が垂直に入射してきた場合の鏡面反射率（よくF0と表記されます）として値が解釈されます。
　なお、アルベドとしての値の場合、従来のディフューズテクスチャと同様に分かりやすい素材の模様だったりしますが、値域がより狭かったり、入射する光の向きによってできた細かいレベルの陰影をきれいに取り除く処理などがなされており、ディフューズテクスチャと全く同じというわけではありません。そして、実際の材質を計測した値を用いるのが通常です。

　ラフネステクスチャの「ラフネス」は「物体表面上の粗さ」（顕微鏡レベルの凹凸の度合い）を表す値が入っています。このラフネスの値が大きいと、その辺りのミクロレベルの表面は凸凹の変化が激しい（マイクロファセットでいうなら、微細平面がより様々な方向を向いている）ことになり、これは物理的には主にスペキュラ反射部分の明瞭さや広がり方の分布に影響してくるのです。

　メタリックは、材質が金属性のものか、そうでない（プラスチックなど）ものか、の区別を表し、通常はテクスチャの部分によって０か１かの両極端な値が入っています（どちらかの区別なので）。
　実は、物体の光の反射は、その物体が金属性のものか、それ以外のものかで、その特性が大きく異なるのです。そのため、その区別をするために、このパラメータが存在しています。

　そして、これらのベースカラーやラフネスといったテクスチャの値は、実際の現実の材質を光学的に計測した、物理的な値が入っています。従来のように、デザイナーが、感覚でフォトショップなどで入れた値ではないのです。

　その計測値は、実際に様々なところで公開されています。

　ただし、これらのラフネスやスペキュラの値は、世に存在するあらゆる物理ベース対応レンダリングエンジン・ゲームエンジンで正しい互換性があるとは限らないことに注意が必要です。

　現時点においてはUnreal EngineやUnity、Frostbiteといった主流のゲームエンジンまたはオフラインレンダラーが、たまたまというか、Disneyが発表した「Disney Principled BRDF」⁹と呼ばれるBRDF、またはそのサブセットに準拠していることが多いため、大体は互換性があるということに過ぎません。¹⁰実際は、各エンジン・ライブラリで微妙に表示結果に違いが見られる可能性もあります。

　この辺りも、いずれ話せればと思います。

4. 「CGの計算の過程において、データの入力から出力装置（ディスプレイなど）までを通じて、正しい取扱いになっている」とは？

　これは、どちらかというと物理的な考慮がどうの、という話とはそもそも異なる話ですが、重要なので項目として入れています。
　さて、「正しい取扱い」とはなんぞやの前に、光の減衰について話をします。

　現実世界では、光は点光源の場合、光の進行距離の二乗に反比例して光の強さが弱くなって（減衰して）いきます。

　これは、幾何学的に考えると理解することができます。

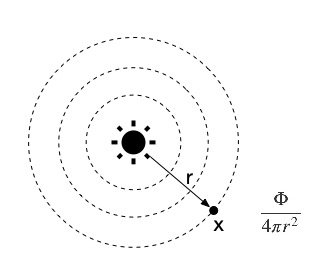
　光源から距離ｒだけ離れると、光源の放射束（光エネルギーの束のようなもの）は四方八方に広がる結果、上図の単位面積xの地点に流れ込む放射束の量は、半径ｒの球の球表面面積$4 \pi r^2$で割れば求めることができます。$4 \pi$は定数なので、実質的には距離の２乗に反比例する、というわけですね。

　しかし、昔のCG時代では、光の進行にともなうこの光の減衰をあえてオフの設定していたり、減衰の程度を弱くすることもよくありました。
　何故かというと、昔のCG制作のワークフローはモニターのガンマの関係の影響をそのまま受けていました。　
　ここではディスプレイガンマの説明はしませんが、要するにコンピュータ内で計算された光は、実際よりも少し暗めにモニタに表示されるのです。

　その結果、CGソフトで３D空間に配置した光は、減衰を「距離の二乗減衰」に設定すると予想以上に光がすぐ弱くなり、物体と光源の距離を少し離しただけでものすごく暗い照り具合になってしまう（一見、そう見えてしまう）ことが多かったのです。そのため、CG制作に慣れていない人は、光源の光の強さをものすごく強い値に設定したりして無理やり辻褄をあわせようとして、その結果シーン全体のライティングバランスが大きく崩れてしまうことがありました。

　現在のきちんとしたCG制作ワークフローでは、そうした入力カラーデータ（画像テクスチャなど）に設定されているガンマをCG計算の最初に解消（リニア化といいます）して計算し、出力時もディスプレイのガンマを意識した調整を行うため、そうした狂いはありません。これをリニアワークフローといいます。

物理ベースレンダリングを行う際においても、光の減衰をきちんと考慮することはもちろん、入力画像やディスプレイのガンマの影響を排除することが必須になってきます。光学計算自体が正確でも、こうしたつまらない部分を怠ると結果が不正確になりますので、間接的に知っておかなければならない知識になります。

※　光の減衰とガンマの話は、理論的には直接的な関係はまったくないのですが、CG制作上、シーンの明るさ調整作業において、微妙に関係してしまうことも多く、そうした意味合いから一緒に説明しました。

　また、より厳密な話でいうと、そもそも色をRGBという３種類の代表的な波長の組み合わせで表現する、大雑把なやり方でよいのか？　という話も出てきます。今後のハイエンドCGでは、光の可視波長の全スペクトルについて人間の分光感度分布を畳み込み計算する方式に移行していくケースも増えていくかもしれません。
　本記事では、そこまでは踏み込まずに、今日のRGB三原色を用いた通常のCGのやり方で話を進めます。

CGのレンダリング計算の仕組み

ローカル反射だけ（GIなし）でも物理ベースの話はできるのか

　今日のCGの計算は、オフラインのレンダラー（レイトレーシング）とリアルタイムCG（ゲームCGなどのラスタライズ式レンダラー）で、大きく方式が異なっています。
　リアルタイムCGにおいては、最近の最新ゲームCGなどでは擬似的に光の複数回反射を取り扱っているのですが、基本的な意味でいうと、GPUによるリアルタイムレンダリングでは、直接光のみしか取り扱うことはできません（環境マップなどを使えばまた別なのですが、とりあえずそれはおいておきます）。

　CGの世界では、ライティング計算は、ローカルなライティングとグローバルなライティングに、概念上分けられることが多いです。

　特に後者は、GI（グローバル・イルミネーション）といって、光の多重反射を考慮して計算することで、現実感あふれるシーンの光の満たされ方を実現する上で、重要な要素となります。リアルタイムCGにおいても、今日ではUnityやUnreal Engineなどのハイエンドエンジンを用いれば、PCなどの高性能機種をターゲットにゲームを作った場合、ほぼ自動でGIが有効になります。

　さて、今日の物理ベースレンダリングですが、広義の意味では、こうしたGIなどの話を含める場合もあります。
　その文脈も人によって様々なので一概には言えないのですが、とはいえ狭義の意味では、GIを伴わないローカル反射（直接光の反射のみ扱った場合）の場合でも、BRDFなどに注目して話せば、それは物理ベースについて話している、と言うことができるでしょう。

　そのため、本シリーズではしばらくは、BRDF（反射モデル）に着目して、ローカル反射に限定して話を進めます。

ローカル反射の仕組み、式の全体像について

ローカル反射（と屈折）の法則

　まず、光がある物体に入射したときに起きる現象について、そもそも論で考えましょう。
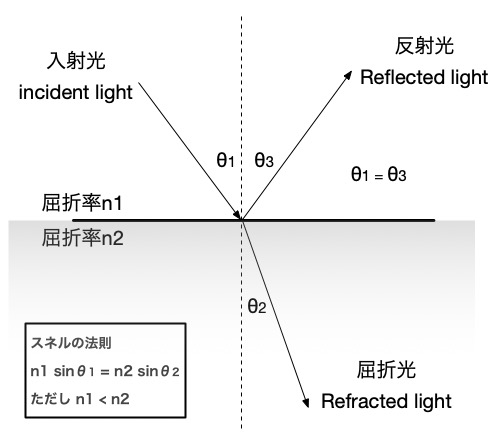
　光がその進み方を変えるときはどういうときかというと、物質の性質が異なる領域にぶつかった時になります。物体を構成する材質は、それぞれ固有の屈折率を持っています。それまで居たものとは異なる屈折率の物体（媒質といいます）に衝突すると、光の一部は反射し、他の一部は屈折します。

　その反射と屈折のそれぞれの角度は、スネルの法則によって計算することができます。
　また、そのうちの反射する光の量の割合は、フレネルの公式によって算出することができます。どちらもCGでは重要な法則です。

　さて、この反射する成分と屈折する成分のうち、反射する成分がspecular反射に該当します。
　また、屈折して新しい物体内部に侵入した光のうち、内部散乱の結果、光がもともといた物体（媒質）の方へ戻っていく光もあります。この戻っていく光がdiffuse反射に該当します。
　もちろん、もともといた媒質に戻るのではなく、そのまま内部で吸収されて熱エネルギーなどに変わってしまう光もあるでしょうし、そのまま新しい物体内部を突き抜けて更に外へ出ていく（物体を透過していく）光もあることでしょう。

　透過していく光については、BRDFではなく、BTDF（Bidirectional Transmittance Distribution Function：双方向透過率分布関数）という関数でその割合を計算することになります。ちなみに、BRDFとBTDFをあわせたものとBSDF（Bidirectional Scattering Distribution Function:双方向散乱分布関数）といいます。

BSDF = BRDF + BTDF

　リアルタイムCGにおいては、BRDFのみで考える（つまり、透過していく光については直接は考えない）ことが多いです。

　このBRDFですが、実際はdiffuse反射用のBRDFとspacular反射用のBRDFに分けて考えます（より本格的な物理ベースBRDFでは、これら以外の種類のBRDFを複合する場合もあります）。

コラム３：　光源の光の強さがそのまま反射して目に届く！？ CGソフトの怪

Lambert反射モデルの話を最初にしましたが、さてここで反射率が$ρ_d = 1.0$だとしましょう。これだと、どんな方向から観察者が反射の様子をのぞき見たときにも、反射光が同じ明るさで目に届くわけですね。
　これって、ある意味すごい（おかしい）ことなのです。

　（半球上の）どんな方向から見ても、というと……それを半球全体で合計してみてください。少なくとも1.0以上の数値に増えてしまうのではないでしょうか。それって、入射した光量より出射する光量のほうが何故か増えている（エネルギー保存則を破っている）ことになりませんか？

　CGソフトを使って物体のマテリアルにLambertを設定したときにも、見た目上は同様のこと（「1.0現象」）が起きています（だからこそ、この誤解が広まるのですが）。何らかのCGソフトを使って、皆さんも試してみてください。

　平行光源を一つおいて、インテンシティ(光の強さ)を1.0に設定、平面ポリゴンを配置しましょう。平面ポリゴンにLambertマテリアルを設定します。diffuse値を1.0（これが$ρ_d=1.0$にあたります）にします。平行光源を平面に垂直になるよう方向づけてください。
　さて、平面ポリゴンの色はどうでしょう。真っ白(1.0)に見えますね？　カメラを動かしていろいろな方向から平面ポリゴンを観察してください。どこから見ても真っ白(1.0)です。

　つまり、強さ1.0の光が、定数1.0のLambert BRDFによって、あらゆる方向へ全く同じ量そのまま反射されているように見えます。エネルギー保存則は一体どこへいったのでしょうか。

　なぜ、こんなことになるのでしょう？　CGソフトにバグでもあるのでしょうか？　いいえ、CGソフトは、一般的なCGデザイナーが扱いやすいように調整されているだけなのです。

　反射光が1.0だった光がもっと小さくなってしまうなど、物理的にはそれがもっともらしい挙動だとしても、デザイナーにとってはそれは非常にわかりにくいのです。CGソフトのマテリアルプロパティ画面のスライダーで、1.0の強さにした光を物体法線に垂直に当てたら、その物体のdiffuse値が1.0にしたのであれば、1.0の明るさでカメラに返ってきて、1.0の明るさでレンダリング画像になってくれたほうが、CGデザイナーにとっては遥かに扱いやすく、直感的なのです。

　CGソフトは、彼らの要求に合わせた仕様になっています。合わせた、といっても明らかに間違った計算にはしていません。CGソフトでは、通常は正規化Lambertというものが使われています。

f_r(x,ω',ω)=\frac{ρ_d}{\pi}

ここで出てくるπってなんでしょう。円周率ですね。なぜこんなモノが。詳細は次回以降に言及しますが、余弦項（コサイン項）すなわちcosθを半球上で積分するとπになります。そのπで$ρ_d$を割ると、Lambertがエネルギー保存則を満たすようになります。これが正規化Lambertと呼ばれるものです。

CGソフトでは、Lambertマテリアルとしてこの正規化Lambertが使われます。しかし、そのままだともちろんπで割られるので、1.0の光量（この文脈では、正確には放射照度といいます）を当てても、出射するのは1.0/πと暗くなります。本来それで（エネルギー保存という意味では）正しいのですが、CGデザイナーにとってはなんだか直感的ではありません。1.0の光を反射率1.0にしたなら、単純に1.0になって返ってきてほしいのです。

そのため、通常、CGにおける通常のライト（専門用語でPunctual Lightと呼びます）の光量は、ユーザーがソフト上のUIで1.0と強さを設定していますが、実はCGソフトが内部でこっそりπを乗算しています。それを実際の反射の計算における入射光の量（放射照度）として扱うことによって、「CGデザイナーの『直感』に沿う意味でのつじつまを合わせている」のです。¹¹

ローカル反射の式全体

　ようやく本題です。本記事ではしばらくBRDFに着目することとしました。
　最初の「おさらい」で、簡単なLambertの計算式を紹介しました。

L_r = \rho_d \times (L \cdot N) \times i_d

　これを、もう少し専門的に捉えてみましょう。

$ρ_d$はディフューズ反射率ということでした。これを、エネルギー保存を満たすよう正規化Lambertで考えてみます。

\frac{\rho_d}{\pi}

この$\rho_d$はより専門的にはディフューズリフレクタンスと呼びます。正確には、入射した放射束と出ていく放射束の比率

\rho_d = \frac{d\Phi_r}{d\Phi_i}

なのですが、放射束などの光の量の種類については次回以降やります。今は大雑把に、「ある場を通り抜けられる光の割合」くらいに思っておいてください。
さて、この正規化lambertですが、これはBRDFなのでしたね。

f_r(x,\vec\omega', \vec\omega) = \frac{\rho_d}{\pi}

「おさらい」のLambert反射の式に戻してみましょう。

L_r(x) = f_r(x,\vec\omega', \vec\omega) \times (L \cdot N) \times i_d

数式に慣れない人のために、あえて明示的に掛け算記号$\times$を入れましたが、省略することができます。

L_r(x) = f_r(x,\vec\omega', \vec\omega) (L \cdot N) i_d

数学では、記号同士がぴたっとくっついているのは、それらが乗算されている関係であることを意味します。
（足し算の場合は、私達の一般の理解と同じで、きちんと足し算記号が付きます）
ちなみに$x$は物体表面上の位置を意味します。

さて、$(L \cdot N) i_d$の部分ですが、これはCGの分野では放射照度（$E$という記号がよく使われます）という明るさであるとされています。

じつは、CGの公式として、ある反射が起きたときに、ある方向へと反射する光（放射輝度）$L_r(x)$は、以下のようにして、BRDFと放射照度の乗算で求めることができるという公式があるのです。¹² ¹³

L_r(x) = f_r(x,\vec\omega', \vec\omega) E(x) \\
ここで、E(x) = \frac{\Phi \cos{\theta}}{4 \pi r^2}

ということは、そうです。今までなんとなくLambert反射のシェーダーを書いていた方、実はきちんとCGの公式に則ってやっていたんですね。
ただし、今までの理解では、式の各項目のどこからどこまでが、どういう意味としてまとめて考えることができるのか、うまく意識できなかったと思います。

Lambert反射モデルなど、一部の反射モデルは$(L \cdot N)$というコサイン項まで含めて反射モデルとうたっているものもあるので、CGを論ずる際に少々話をややこしいものにしています。しかし、厳密にBRDFという点でみると、このコサイン項は切り離して考えなくてはなりません。Lambert反射モデルはBRDFという点でみると、定数なのです。

さて、長くなりましたが結論を言うと、ローカル反射における物理ベースレンダリングというのは、ようはこの

L_r(x) = f_r(x,\vec\omega', \vec\omega) E(x)

または$E(x)=(L \cdot N) i_d$なのでもう少し馴染みのある書き方にすると、

L_r(x) = f_r(x,\vec\omega', \vec\omega) (L \cdot N) i_d

の計算式における、BRDFつまり$f_r(x,\vec\omega', \vec\omega)$の式を、より物理的根拠に基づいたBRDFに取り替えればよいのです。
「良いのです」というか、これだけをもって「よっしゃ！オレ物理ベース完全に理解した」とか思われちゃうと、すごく困るというか……きっと私が多方面からマサカリを食らうことになるのですが。

　少なくとも、理解の第一歩であることは間違いありません。実際はもっと学ばなければならないことがたくさんありますが、理解の一歩としてはそんなに難しくないと思いませんか？
　少なくとも、今までの反射計算の延長線として考えながら学んでいくことができると思います。

　ちなみに、皆さんがどこかで物理ベースな話題として聞いたことのある、「GGX」などの単語は、その物理ベースなBRDF $f_r(x,\vec\omega', \vec\omega)$の構成物（計算項）として登場します。次回以降、その領域にも踏み込んでいきましょう。

※　BRDFと放射照度を計算すれば良い、と書きましたが、実際はもう少し複雑に計算しなければならないケースもあります。ポイントライトやディレクショナルライトのみで照らすような単純なケースではない場合（間接光を考慮する場合や環境マップ、エリアライト（面積を持っているタイプの光源）を光源とする場合など）です。その場合は、半球面上での積分計算が必要になります。まぁ、難しいと思うので今はそういう計算方法もあるのだな、くらいに考えておいてください。

L_r(x, \vec \omega) = \int_\Omega f_r(x, \vec \omega', \vec \omega)(\vec n \cdot \vec \omega') L_i(x, \vec \omega') d \vec \omega'

第１回目のおわりに

　さて、冒頭に書いたとおり、敷居を低くするために、本当に極力、数式を使いませんでした。BRDFの用語に言及しているにもかかわらず定義の式をかかないとか、放射輝度や放射照度、放射束という用語を出しているのにちゃんと説明しないとか、ある意味、狂気の沙汰ですが、２回目以降はちゃんと説明します。

　CGの専門家の方、またはCGを数式から逃げずにきちんと勉強したいと思われている方にとっては、本記事は式の導出など一切やっていません（むしろ避けている）ので、非常にけったいな記事に感じられると思います。

　しかし、本来正攻法であるそうした学び方に、数学の素養のない多くの方は正直ついていけない部分もあり、私が物理ベースの話をしてもなかなか分かってもらえない、学ぼうとしてもらえないことも多く、少々寂しい思いがありました。
　それでも、PBR、物理ベースレンダリングはホットな話題ですし、できれば理解したい！　という方は多いだろうと思い、「では思い切ってゆるふわに説明しちゃえばどうよ！？」と思いたち、本記事を書いた次第です。

　ゆるふわとはいえ、明らかな間違いや、むしろ誤解を招くような変なたとえなどはできるだけ使わないように気をつけたつもりではあるのですが、なにぶん私も勉強中の身ですので、大きな勘違いやミスをやってしまっている部分もあるかもしれません。その時は、遠慮なくご指摘をいただけますと幸いです。

　ちなみに、今回はこんなでしたが、回を追うごとに、内容の厳密性を上げていこうと思っています。

　長い記事でしたが、お付き合いくださいましてありがとうございます。
　第２回目はdiffuse BRDFについてです。

少し回りくどい言い方ですね。「物理的に正しい」という言い方は、CGの専門家である人ほど避けます。「物理的に正しい」というと本当に「物理的に完璧に正しい（完璧に再現できる）」というニュアンスがあり、そのようなレンダリングは現行不可能だからです。CG理論的にも、ある程度の物理根拠でそれ以上は諦める場合も多く、そうした中で「物理的に正しい！」などと言い切ってしまうと、それはCGを専門とする人にとっては、大言壮語に聞こえてしまうようです。 ↩
BRDFには多くの種類があり、完全にはエネルギー保存していないものが大半です。しかしPBR時代以前に用いられていたBRDFよりも、PBR普及期以降に登場したBRDFの方がエネルギー保存についてより考慮されていると言っていいでしょう。また、エネルギー保存を満たすように補完するテクニックも登場しています。 ↩
エネルギー保存については満たした正規化Phongと呼ばれるBRDFも存在します。 ↩
いわゆる環境光という、明るさを一定のレベルにかさ上げする定数項のこと ↩
さらに、Phongのspacular反射の他に、それをより計算コストを軽くしたBlinn-Phongというモデルもあります。ややこしいですね。ちなみに、昔のGPUの固定レンダリングパイプラインでサポートされていた「Phong」は、ハーフベクトルを使ったより計算の軽いBlinn-Phongの方です。 ↩
いわゆるノーマルマッピングで扱う凹凸よりも、ずっとミクロなレベルの凹凸の話であることに注意です。マイクロファセットのスケールは「マイクロスケール」、一方のノーマルマップのスケールは「メソスケール」と呼ばれます。 ↩
「エネルギー保存則を満たす、満たさない」も、１か０かの話ではなく、完全に満たしていないBRDFやケースがあるからといって、それらが必ずしもダメというわけではありません。本記事でPBRの要件として掲げてはいますが、「エネルギー保存則が絶対正義」ではないのです。現行で世に受け入れられているDisney Principled BRDFなどもそうですが、BRDFの世界では物理的厳密さよりもCGアーティストからみた扱いやすさのために、物理理論を棚上げにした調整（「アドホックな調整」などと言われたりします）が入っているものも存在します。重要なのは、そのBRDFの性質をよく知って運用することです。 ↩
実は、エネルギー保存則を考慮した「正規化Lambert」や「正規化Phong」といったBRDFもあるのですが、別の話にしましょう。 ↩
Brent Burley, “Physically Based Shading at Disney”, SIGGRAPH 2012 Course: Practical Physically Based Shading in Film and Game Production, ↩
あの後更に調べましたが、Disneyによる「Disney Principled BRDF」によって広まったMetallic-Roughness型の物理パラメーターは、ゲーム業界では標準的な存在になっていますが、オフラインレンダラーで対応しているものはまだまだ少数派のようです（最近ではVRayがVRay-Nextで対応）。オフラインレンダラーの世界では、Specular-Glossiness型という、また少し別の種類の物理パラメーターで物理レンダリングを行う事が多いです。ただし、パラメーターの種類と取り回し方が少し異なるだけで、基本的な考え方は同じです。 ↩
CGソフトや使用するマテリアル・ライトの組み合わせによってはπを乗算しないものもあると思います。近年は物理ベースを意識したライティングのフローが普及しているので、このあたりの事情は徐々に変わっていきそうです。 ↩
$、E(x) = \frac{\Phi \cos{\theta}}{4 \pi r^2}$ という式がいきなり出てきましたが、すぐわからなくても落ち込まないでください。先程の光の減衰の公式（図）と、コサイン項による光の薄まりの式（図）を思い出してください。その両方を考慮（乗算）した結果、こういう式の形で放射照度となるわけです。 ↩
ただし、スペキュラBRDFの場合はBRDFがライトベクトルの情報を必要とするため、ライトベクトル無しで純粋な放射照度（イラディアンス）のみだと、普通には計算が行なえないことには注意が必要です。 ↩

物理ベースレンダリングを柔らかく説明してみる（１）