物理ベースレンダリングを柔らかく説明してみる（２）

はじめに

• 本記事は、「シェーダーを触り始めてLambertやPhong反射までは作れる」くらいのレベルを最低ラインとして読者層を想定しています
• 説明の厳密さより、感覚的にイメージの湧きやすい説明の仕方を重視します。数式も少なめです。
• 厳密な説明を求める方は、他の記事にあたってください。
• 第１回についてはこちらをどうぞ。

今ふたたび、古典的ライティングから考えてみよう

　前回の記事の最初では、Lambert反射の式を振り返りました。ここでは、もう少し進んでPhong反射モデルをおさらいしましょう。
Phong反射モデルは、Lambert反射に加えて、独自のSpecular反射光と環境光の成分があるんでしたね。

L_r = ρ_d(L \cdot N)i_d + ρ_s(R \cdot V)^α i_s + k_a i_a

specular反射の項は、明確にBRDFと$(L \cdot N)$を分離した書き方にしてみましょう。

L_r = ρ_d(L \cdot N)i_d + \frac{ρ_s(R \cdot V)^α}{(L \cdot N)} (L \cdot N) i_s + k_a i_a

ここで、 $ρ_d$ と $ \frac{ρ_s(R \cdot V)^α}{(L \cdot N)} $ はそれぞれBRDF（Lambert BRDFとPhong Specular BRDF）なのでしたね。

　それぞれ $f_{rd}$ と $f_{rs}$ と表示するとして、式を次のように一般化することができます。

L_r = f_{rd}(x,\vec \omega', \vec \omega)(L \cdot N)i_d + f_{rs}(x,\vec \omega', \vec \omega) (L \cdot N) i_s + k_a i_a

ここで、一般的には１項目の $f_{rd}(x,\vec \omega', \vec \omega)$ をdiffuse BRDF、２項目の $f_{rs}(x,\vec \omega', \vec \omega)$ をSpecular BRDFと呼びます。

　つまり、「物体の光の反射は（前回説明したように）diffuse反射とspecular反射に大別されるのだから、それぞれを別々のBRDFで適切に処理して合成してあげればよいではないか」、ということです。
　実際の物理ベースレンダリングの計算式でも、大体はこのような形になっています。もっとも、実際はdiffuse反射とspecular反射をただ足すのではなく、エネルギー保存則を考慮した合成の仕方が取られるのですが（とはいえ、現行主流のモデルだと線形補間に近いものが結構多いです）。

　さらに、diffuse BRDFやspecular BRDFだけでなく、それ以外の表現を行えるBRDFを組み合わせる反射モデルも存在します。このように、複数のBRDFを複合させたものを複合BRDFモデルと呼んだりします。

　さて、ここまでを大前提として、次にこれらdiffuse BRDFとspecular BRDFを見ていきましょう。

diffuse反射（拡散反射）とはそもそも何なのか

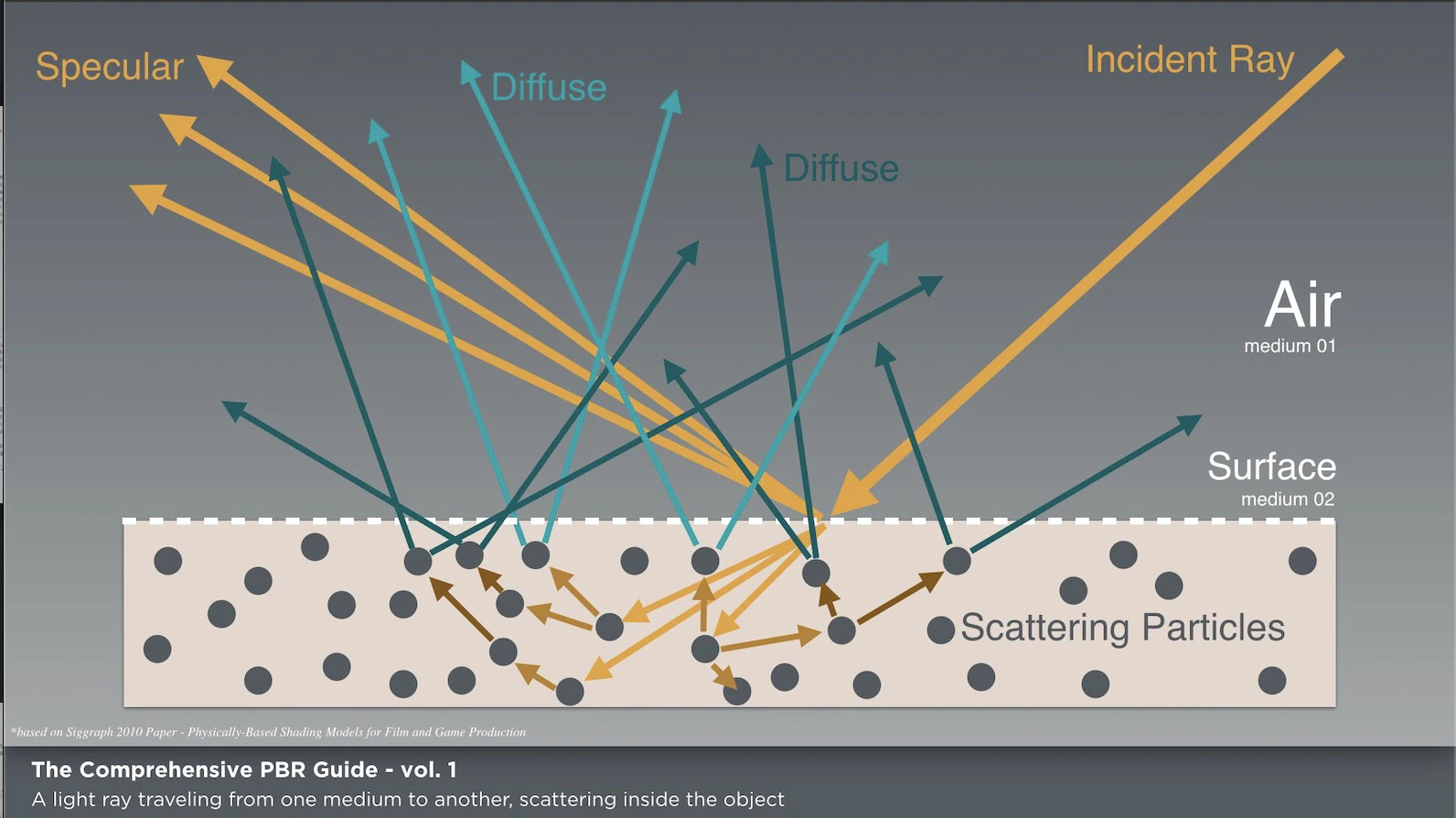
Wes McDermott「The Comprehensive PBR Guide by Allegorithmic - vol. 1 Light and Matter : The theory of Physically-Based Rendering and Shading」©Allegorithmic　から引用

　ランバート反射など、我々は気ままに拡散反射式を実装していたりしますが、そもそもdiffuse反射（拡散反射）とは光学現象としてはどういうものとして捉えればよいのでしょうか？
　結論から言うと、diffuse反射は「光が物体と衝突して、そのうち屈折して物体内に侵入した分が、散乱現象の結果再び物体表面の外へ出ていく」の現象を扱う反射モデルです。

　ここで、少しCGを学ばれた方ははっとするかもしれません。「ん？　物体内に屈折して侵入して散乱して……それはいわゆる、表面下散乱（サブサーフェース・スキャタリングでは？」そのとおり、この光学現象は、本来サブサーフェーススキャタリングとして真面目に取り扱わなければならない現象です。diffuse反射は厳密に考えると、反射というよりも、散乱現象なんですね。

　しかし、「物は見方」ということわざがあります。表面下散乱現象では、物体ごとに固有の「光が表面下で散乱する距離（表面下散乱距離と呼ばれます）」があります。例えば、人間の皮膚であればせいぜい１センチくらいかもしれません。もし、人間の皮膚よりももっと表面下散乱距離が十分に短い物体（プラスチックなど）があったとして、それをレンダリングするシーンが、それほどその物体にカメラが接近していないような状況であるなら……。その表面下散乱距離を無視してしまう、という大胆な近似を考えることができます。

　もう少し具体的に言うと、「入射した光が、表面下で散乱はするけれども、表層に出てくる位置が入射位置と同じである」とみなすことで、レンダリング計算としては非常に単純化したモデルとして捉え直すことができるのです。これが、いわゆる広く知られたランバート反射などの（表面下散乱計算を真面目に計算しない）diffuse反射実装というわけです。

　逆に言えば、表面下散乱距離がそれほど短くない物体、または、表面下散乱距離が短いけれども、カメラがその物体に非常に近づいており、レンダリングされる物体のピクセル面積と対比して考えると、いくら短いとはいえ流石に無視できない長さである……という場合は、単純なdiffuse BRDF反射としてではなく、サブサーフェイススキャタリングの各種技法で真面目に表面下散乱を計算しないと、説得力のあるレンダリング結果にならない可能性があります。

　ここで注意なのは、「diffuse反射」という言葉のCG理論的な意味あいとしては、とにかく「物体内に潜った光が散乱の結果、再び表上に出ていく」現象を指しており、それをどうCGレンダリング実装として処理するか（ランバート反射などで簡易に処理するか、表面下散乱計算を真面目に計算するか）は問いていないということです。

　しかし、文脈として「diffuse反射」をCGの実装という意味で使う局面もあります。この場合、表面下散乱を真面目に計算しない¹（ランバート反射や後述するBurley diffuse BRDFなどの）反射計算実装を指す場合が多いでしょう。この場合も（CG実装技法的な意味での）表面下散乱（サブサーフェーススキャタリング）¹　は成分としてきちんと含まれています。例えば、ランバート反射が表面下散乱を真面目に計算していないからといって、CG実装で表面下散乱を真面目に計算する際の光の成分を計算結果にいれていないわけではありません。まともに計算しないでdiffuseアルベドという定数で大雑把に済ませているだけです。

　なので、diffuse反射の話をするときに、CGで実装をどこまで真面目にやるかの話をする時は、文脈に少し注意が必要かもしれませんね。

　少し長くなりましたが、（表面下散乱を真面目に計算しない）diffuse反射実装とサブサーフェーススキャタリング実装。CGの計算処理（実装）としてはまるで別物と思われていた両者が、光学現象として考えると実は同じものを指しており、そのスケールに応じてCGとしての扱いを（真面目にやるか大胆に近似するか）変えていたに過ぎなかった、というのは驚きですね。

diffuse BRDF

さて、diffuse反射におけるBRDFにはどういったものが使われるのでしょうか。

正規化Lambert

少なくともゲームCGの世界では、意外や意外、フツーにLambertが使われていたりすることが多いのです（といっても、エネルギー保存を考えて実際には正規化Lambertが使われます）。

f_{rd}(x,\vec \omega', \vec \omega) = \frac{\rho_d}{\pi}

定数なので、実際には位置xにしか依存しない関数ですから

f_{rd}(x) = \frac{\rho_d}{\pi}

と書いた方がより正確ですね。

実際には、物理的根拠に基づいて考案されたdiffuse BRDFが世にはあるのですが、どうも計算の重さの割に、Specular BRDFほどの目立った反射品質の向上を果たせないと評価されることが多いようです。²
ということで、ゲームCGなどでは不採用になってしまうことが多いようですね。現時点ではUnreal Engineですら、（一時期を除いて）ほぼ正規化Lambertを使っているようです。³

とはいえ、本記事はお勉強ですから、他のdiffuse BRDFもご紹介しましょう。

Oren Nayar BRDF（オーレン・ネイヤーBRDF）

1994年、Michael Oren と Shree K. Nayarによって発表されたdiffuse反射BRDFです。⁴
物体表面を粗い面（粗面）と仮定し、その表面の微細構造をマイクロファセットとして考えることで、コンクリート・石膏・砂などのより現実の材質表面の再現性を向上させました。マイクロファセットの粗さはラフネスというパラメータ値でコントロールすることができ、値が大きいほど微細平面の凹みの規模・量は増え、微細構造上の光の相互のインタラクション（マスキング、シャドウイング、相互反射など）を発生させます。

　※マスキング、シャドウイング、相互反射については、後半でまた説明します。

　一方、ラフネスが０の場合、計算上Lambertの特性に一致するようになります。そのため、Oren Nayar BRDFはdiffuse反射を（Lambert反射を含む）一般化するBRDFの１つとして考えることができます。

肝心のOren Nayar BRDFの式ですが、難しい数式を極力さけて敷居を下げようという本記事においては複雑すぎるため、ここではあえて割愛します。 @mebiusbox2 様が「拡散BRDF」という記事でまさに式の導出まで含めて詳しく説明してくださっていますので、意欲のある方はそちらをご覧ください。

　ちなみに、Oren-Nayarモデルにおけるラフネスはスペキュラー反射で今日主流のCook-Torranceモデルのラフネスとは互換性がないためその点は注意です。

Disney (Burley) diffuse BRDF

Disney diffuse BRDFや　Burley diffuse BRDFなどと呼ばれたりします。

f_{d} = \frac{\sigma}{\pi}(1+(F_{D90}-1)(1-\cos\theta_{l})^5)
(1+(F_{D90}-1)(1-\cos\theta_{v})^5) \\
ここで F_{D90} = 0.5 + 2 roughness \cos^2(\theta_{d})

$\theta_l$は光の入射方向ベクトル、$\theta_v$　は視線ベクトル、$\theta_d$はハーフベクトルと光の入射方向ベクトルの間の角度です。ハーフベクトルというのは、光の入射方向ベクトルと視線ベクトルの中間のベクトルのことをいいます。

h = \frac{\vec{v}+\vec{l}}{|\vec{v}+\vec{l}|}

なんだかこの時点で複雑に見えますが、正規化Lambertである$\frac{\rho}{\pi}$の部分が見えますね。もちろんこの部分が基本のベースです。で、これの後ろに長い部分が乗算でくっついていますが、要はこの後ろの部分はフレネル効果を表してます。
　なんでこういう物を付けたのかというと、論文によれば普通のLambertではシェーディングの境界部分が実際の材質よりも暗くなりすぎるきらいがあり、粗さによってフレネル反射率を操作することにより（本来はフレネル反射率は屈折率次第なのですが、この手法では粗さ＝ラフネスで操作しています）境界部分の明るさを調整できるようにした、とのことです。
それがまさに

F_{D90} = 0.5 + 2 roughness \cos^2(\theta_{d})

の部分です。ラフネスが0なら0.5、ラフネスが１なら2.5まで上昇します。おそらくこれが、審美的に良いとされたのでしょう。うーん。そこはかとなくアドホック感。
　とはいえこのBurley Diffuse、経験則的なモデルながらも、MERL100という様々な現実の材質のBRDF実測データとの照合を行い、ほぼほぼそれらのデータと傾向がマッチすることは確かめられているようです。
　ちなみにEA(Electronic Arts)社のゲームエンジンであるFrostbiteエンジンはこのBurley Diffuse（のエネルギー保存を考慮した正規化版）を採用しているようです。

補足：シャドウイング、マスキング、相互反射について

物理ベースなBRDFでは、BRDFの一部を構成する要素、考え方として「幾何減衰」というものがあります。マイクロファセット面における、様々な方向を向いた平面同士の光の相互作用を幾何学的に考慮したものです。

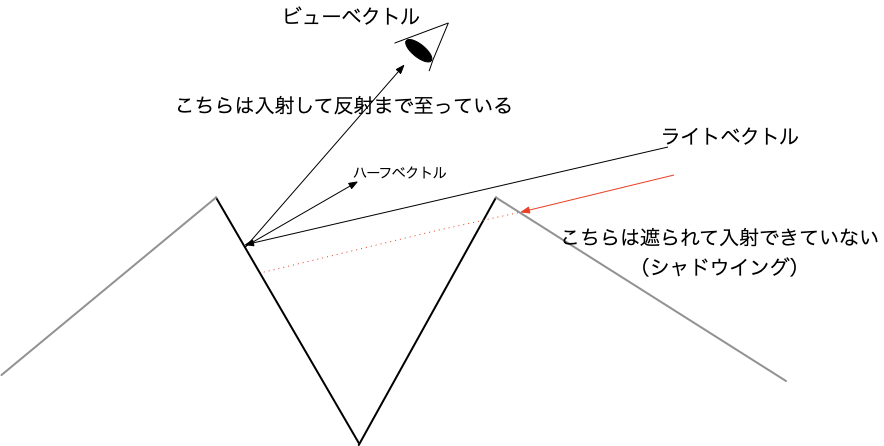
シャドウイング

マスキング

上記のシャドウイングとマスキングが同時におきる場合もあります。

また、Oren Nayarなどの場合、さらに相互反射を考えるケースもあります。

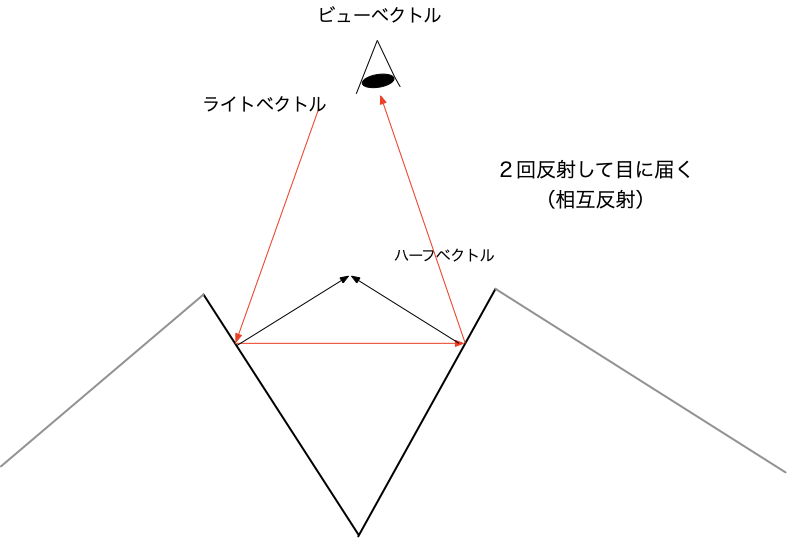
相互反射

おわりに

さて、次回３回目はspecular BRDFの紹介に移ります。皆様もどこかで見たことがあるであろう、でもなんか今までわかったようでよくわからなかった、Cook Torranceの式がいよいよ出てきます。$f_r = \frac{D G F}{4 \cos \theta_v \cos \theta_l}$っていうアレです。
※すみません、specular BRDFに行く前に少し寄り道な内容をやります。

　とはいえ、このシリーズ、specular BRDFまで紹介してハイ終わり、にはしないつもりです。

　実際、diffuse BRDFとspecular BRDFを実装しても、点光源や平行光源だけで照らしただけではまったく物理ベースのリアルな雰囲気が出てこないのです。そこで次々回以降では、IBL（イメージベースドライティング）の話もすることになると思います。また、Disney Principled BRDFやUnreal Engineで採用されたBRDFなどの、既存の実践的な事例もご紹介したいと思います。

1. ここで「真面目に計算しない」ではなく「考慮しない」という言い方を使ってしまうと語弊が生まれそうです。考慮しないだと、計算成分として含めないという意味合いも出てきてしまうかもしれませんからね。 ↩ ↩²

2. どれだけうまく考えたdiffuse BRDFでもやはりエネルギー保存は考慮しなければならず、そうすると今度は正規化Lambertと限りなく見た目が近づいてしまうようです。確かにそれではゲームで使うメリットは薄そうですね。 ↩

3. とはいえごく最近でいうと、Lambertではない、複雑なdiffuse BRDFを採用するタイトルやエンジンも出てきています。 ↩

4. M. Oren and S.K. Nayar, "Generalization of Lambert's Reflectance Model". SIGGRAPH. pp.239-246, Jul, 1994 ↩